QT 状态机的使用
QT 状态机的使用场景:
QT 状态机适用于需要管理复杂状态和状态转换的场景,例如游戏开发、UI界面控制、自动化控制系统等。它可以帮助组织和管理程序中的各种状态,并定义状态之间的转换规则,使程序逻辑清晰、易于维护。
QT 状态机的优点:
- 清晰的状态管理:通过状态机可以清晰地定义和管理程序中的各种状态,使程序逻辑更加明确。
- 易于扩展和维护:状态机的状态和状态转换规则可以灵活地扩展和修改,便于后续维护和修改。
- 可视化设计:QT Creator提供了状态机编辑器,可以通过图形化界面设计状态机,提高开发效率。
- 事件驱动:状态机可以响应外部事件触发状态转换,实现事件驱动的程序设计。
QT 状态机的缺点:
- 学习成本:对于初学者来说,理解状态机的概念和使用方法可能需要一定的学习成本。
- 复杂状态机设计:在处理复杂的状态转换逻辑时,可能需要仔细设计状态机的状态和转换规则,增加开发难度。
- 性能开销:在某些情况下,使用状态机可能会引入一定的性能开销,需要根据实际情况进行评估。
QT 状态机的代码示例:
以下是一个简单的 QT 状态机示例,演示了如何使用 QT 状态机实现一个简单的灯泡控制系统:
#include <QCoreApplication>
#include <QStateMachine>
#include <QState>
#include <QDebug>int main(int argc, char *argv[]) {QCoreApplication app(argc, argv);// 创建状态机QStateMachine machine;// 创建三个状态:关闭、开启、闪烁QState *offState = new QState();offState->assignProperty(灯泡, "color", "gray");QState *onState = new QState();onState->assignProperty(灯泡, "color", "yellow");QState *blinkState = new QState();blinkState->assignProperty(灯泡, "color", "red");// 设置状态转换规则offState->addTransition(按钮, SIGNAL(clicked()), onState);onState->addTransition(按钮, SIGNAL(clicked()), offState);onState->addTransition(按钮, SIGNAL(doubleClicked()), blinkState);blinkState->addTransition(按钮, SIGNAL(clicked()), offState);// 将状态添加到状态机machine.addState(offState);machine.addState(onState);machine.addState(blinkState);// 设置初始状态machine.setInitialState(offState);// 启动状态机machine.start();return app.exec();
}
在这个例子中,我们创建了一个简单的灯泡控制系统,包括三个状态:关闭、开启和闪烁。通过按钮的点击事件触发状态之间的转换。通过状态机的设计,可以清晰地管理灯泡的状态和状态转换规则,实现灯泡的控制逻辑。
相关文章:

QT 状态机的使用
QT 状态机的使用场景: QT 状态机适用于需要管理复杂状态和状态转换的场景,例如游戏开发、UI界面控制、自动化控制系统等。它可以帮助组织和管理程序中的各种状态,并定义状态之间的转换规则,使程序逻辑清晰、易于维护。 QT 状态机…...

走进volatile的世界,探索它与可见性,有序性,原子性之间的爱恨情仇!
写在开头 在之前的几篇博文中,我们都提到了 volatile 关键字,这个单词中文释义为:不稳定的,易挥发的,在Java中代表变量修饰符,用来修饰会被不同线程访问和修改的变量,对于方法,代码…...
:python爬虫完整学习大纲)
python从入门到精通(十五):python爬虫完整学习大纲
一、基础知识 爬虫的基本概念和工作原理。 HTTP 协议和网页结构。 Python 爬虫开发的基础库,如 requests、BeautifulSoup 等。 常见的反爬虫机制和应对方法。 二、爬虫逆向的技术 代理服务器和 IP 封锁突破。 用户代理和请求头模拟。 JavaScript 解析和执行。 验证码…...

为什么JDK8.0 之后允许接口定义静态方法和默认方法呢?
为什么JDK8.0 之后允许接口定义静态方法和默认方法呢? 因为它违反了接口作为一个抽象标准定义的概念。** 静态方法:因为之前的标准类库设计中,有很多Collection/Colletions或者Path/Paths这样成对的接口和类,后面的类中都是静态…...

如何通过生成式AI增强人类的创造力
如何通过生成式AI增强人类的创造力 概述: 生成式AI(人工智能),能创建新的文本、图像和视频内容,不仅仍有成为取代许多工作岗位的潜力,但其最大的机遇在于增强人类创造力,助力商业和政府克服创新…...
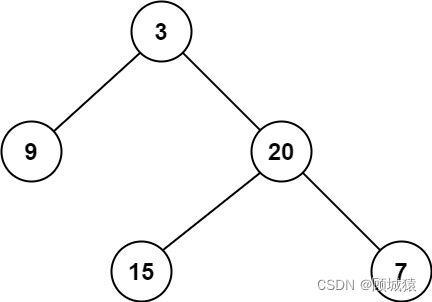
力扣111---二叉树的最小深度(简单题,Java,递归+非递归)
目录 题目描述: (递归)代码: (非递归、层次遍历)代码: 题目描述: 给定一个二叉树,找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说…...

C#处理文件
目录 1.管理文件2.管理驱动器3.管理目录4.管理路径5.获取文件信息6.控制如何处理文件 1.管理文件 C# 中使用 File 类可以进行文件的读取、写入和删除操作。File 类提供了多个静态方法来处理文件,如 File.Exists() 用于检查文件是否存在,File.ReadAllTex…...

git |常用命令
git 命令 非常常用 主流的仓库管理服务器,svn 和git 接下来,介绍git 操作(自用 先讲一个简单的demo 流程 环境:centos、git #先创建一个本地 git 文件夹 mkdir test && cd ./test #写一个README.md #echo “# 张不大 的de…...

力扣100热题:两、三、四数之和,哈希+数组+双指针+排序
目录 一、两数之和 二、两数之和 II - 输入有序数组 三、两数之和 III - 数据结构设计 四、两数之和 IV - 输入 BST(二叉搜索树) 五、三数之和 六、四数之和 一、两数之和 题目:1. 两数之和 参考力扣题解:. - 力扣&#x…...
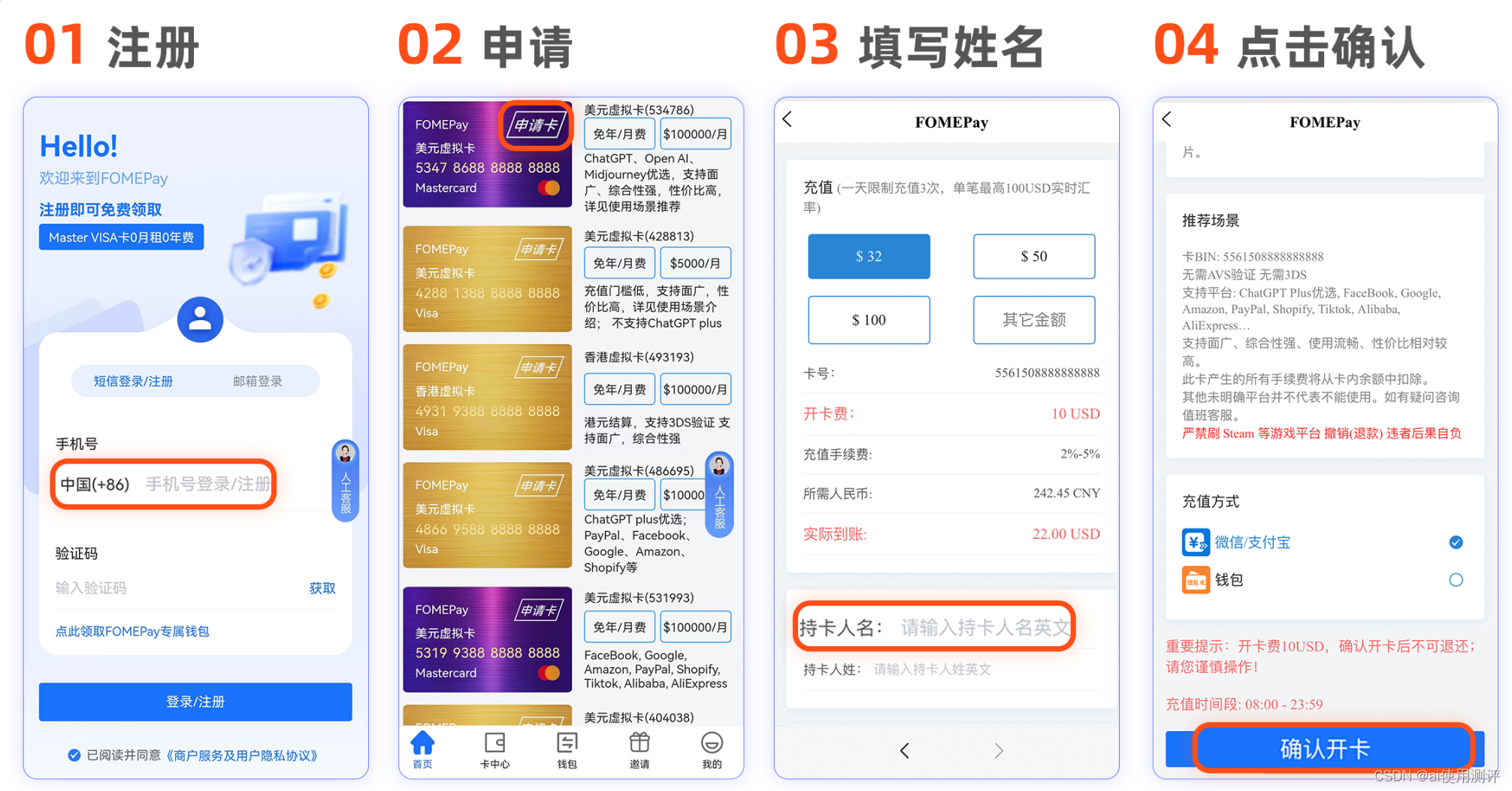
国外visa卡怎么办理,可充ChatGPTPLUS、Claude、Midjourney
很多小伙都在使用ChatGPT,但是想充值ChatGPTPLUS缺需要国外的visa卡,拿自己的银联卡,尝试了好多次还是不行,其实用一张国外的visa卡几分钟就可以升级好 办理国外visa卡,点击获取 国外的visa卡,具体要看你…...

【Web】记录[长城杯 2022 高校组]b4bycoffee题目复现
目录 前言 环境准备 简单分析 EXP 前言 本地jar包运行打通了,远程500,nss靶机有问题,换了bugku就可( 主要记录下做题过程,纯菜狗,小白文 环境准备 这次附件给的jar包是可执行jar,不是可依赖jar&…...

C++ 多路音频pcm混音算法
1、均值化混音算法 不适合商用,声音的损失比较大,不建议用,建议用第二种声音混音 short remix(short pcm1,short pcm2){ int value pcm1 pcm2; return (short)(value/2) } 2、归一化混音算法 输入数据为48Khz-2-16bit音频数据 方法&#…...

Golang 泛型定义类型的时候前面 ~ 代表什么意思
先看代码,定义一个简单的泛型 c1 里面一个 int ,定义一个函数goods 下面 main函数进行调用, 如果直接传int 类型是不会报错的,但是如果传自定义类型的b就会报错。 type c1 interface {int }func goods[T c1](a T) {fmt.Println(a) }type myint intfunc …...

泽众云真机-机型支持ADB调试功能即将上线
最近云真机平台在线客服,收到很多咨询关于ADB调试功能,什么时候能更新?据小编所知,正在升级之中,有一块专门为了解决ADB调试功能提前准备,升级网络硬件设备,目前平台的功能已开发完成࿰…...

基于springboot的购物商城管理系统
1.项目简介 1.1 用户简介 用户主要分为管理员和用户端: 管理员: 管理员可以对后台数据进行管理、拥有最高权限、具体权限有登录后进行首页轮播图的配置管理、商品的配置、新品家具商城的配置管理、、家具商城分类管理配置、家具商城详情商品管理、用户…...
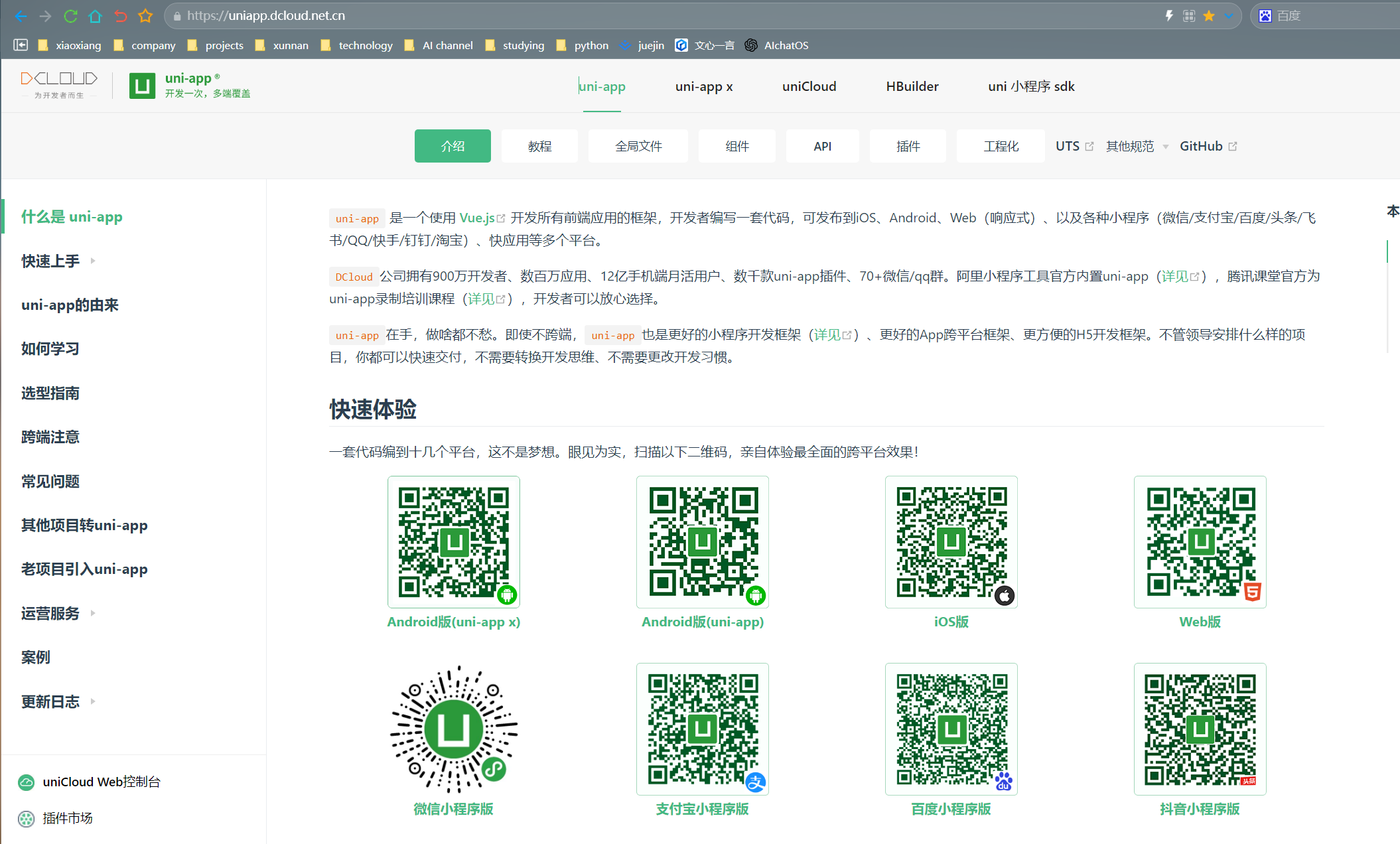
uni-app开发特点和开发流程
uni-app是一个基于Vue.js框架的跨平台应用开发框架,通过一套代码可以同时运行在多个平台上,包括iOS、Android、H5等。它采用了基于流布局的页面渲染机制,可以自动适配不同平台的屏幕尺寸和分辨率。uniapp官网:https://uniapp.dclo…...
Sentinel篇:线程隔离和熔断降级
书接上回:微服务:Sentinel篇 3. 隔离和降级 限流是一种预防措施,虽然限流可以尽量避免因高并发而引起的服务故障,但服务还会因为其它原因而故障。 而要将这些故障控制在一定范围,避免雪崩,就要靠线程隔离…...

HTML静态网页成品作业(HTML+CSS)——家乡广州介绍设计制作(5个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有5个页面。 二、作品演示 三、代…...
【Java IO流】缓冲流和对象流的解析和应用实例
目录 前言 一、缓冲流 四种方式拷贝文件的用时对比 二、对象流 1. 使用对象流写入对象到本地文件 2. 使用对象流读取对象数据 总结 前言 【File文件管理及IO流(基本流)】http://t.csdnimg.cn/uG5Ff 该篇博客中,介绍了学习高级流需要的…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:Select)
提供下拉选择菜单,可以让用户在多个选项之间选择。 说明: 该组件从API Version 8开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 子组件 无 接口 Select(options: Array<SelectOption>) 参数:…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
