九种背包问题(C++)
0-1背包,背包大小target,占用容积vec[i][0],可以带来的利益是vec[i][1]
一件物品只能取一次,先遍历物品然后遍历背包更新不同容积下最大的利益
int func(vector<vector<int>>&vec,int target){vector<int>dp(target+1,0);for(int i=0;i<vec.size();i++){for(int w=target;w>=vec[i][0];w--){dp[w]=max(dp[w-vec[i][0]]+vec[i][1],dp[w]);}}return dp[w];
}
完全背包,与0-1背包相比差别在于物品可以多次选择了
思路和0-1背包差不多,只不过遍历背包容积时从低到高,每次更新时之前都是包含当前物品最优
int func1(vector<vector<int>>&vec,int target){vector<int>dp(target+1,0);for(int i=0;i<vec.size();i++){for(int w=vec[i][0];w<=target;w++){dp[w]=max(dp[w-vec[i][0]]+vec[i][1],dp[w]);}}return dp[w];
}
多重背包,每种物品有vec[i][j][2]个
思路1,二进制商品拆分(比如:111可以组合成1-6任意数字),转化为0-1背包问题
int func2(vector<vector<int>>&vec,int target){int n=vec.size();vector<pair<int,int>>goods;for(auto&i:vec){for(int j=1;j<=i[2];i*=2){i[2]=i[2]-j;goods.push_back({i[0]*j,i[1]*j});}goods.push_back({i[2]*i[0],i[2]*i[1]});}vector<int>dp(target+1,0);for(int i=0;i<goods.size();i++){for(int j=target;j>=goods[i].first;j--){dp[j]=max(dp[j],dp[j-goods[i].first]+goods[i].second);}}return dp[target];
}
思路2 添加物品数量层遍历
int func3(vector<vector<int>>&vec,int target){vector<int>dp(target+1,0);for(int i=0;i<vec.size();i++){for(int j=target;j>=vec[i][0];j--){for(int k=1;k*vec[i][0]<j&&k<=vec[i][2];k++){dp[j]=max(dp[j],dp[j-k*vec[i][0]]+k*vec[i][1]);}}}return dp[target];
}
混合背包,背包中的物品可以有无限个或者有限个
vec[i][0]重量,vec[i][1]价值,vec[i][2]数量
int func4(vector<vector<int>>&vec,int target){vector<int>dp(target+1,0);for(int i=0;i<vec.size();i++){if(vec[i][2]==0){for(int j=vec[i][0];j<=target;j++){dp[j]=max(dp[j],dp[j-vec[i][0]]+vec[i][1]);}}else {for(int j=target;j>=vec[i][0];j--){for(int k=1;k*vec[i][0]<j&&k<=vec[i][2];k++){dp[j]=max(dp[j],dp[j-k*vec[i][0]]+k*vec[i][1]);}}}}return dp[target];
}
分组背包
商品分组,每组最多只能选一个,vec[i][k][0]重量,vec[i][k][1]价值
int func5(vector<vector<vector<int>>>&vec,int target){vector<int>dp(target+1,0);for(int i=0;i<vec.size();i++){for(int j=target;j>=0;j--){//遍历背包容积for(int k=0;k<vec[i].size();k++){//遍历商品组内商品if(j>=vec[i][k][0]) dp[j]=max(dp[j],dp[j-vec[i][k][0]]+vec[i][k][1]);}}}return dp[target];
}
二维背包
约束条件增加,vec[i][0]价值,vec[i][1]是第一个约束条件,vec[i][2]是第二个约束条件
int func6(vector<vector<int>>&vec,int target1,int target2){vector<vector<int>>dp(target1+1,vector<int>(target2+1,0));for(int i=0;i<vec.size();i++){for(int j=target1;j>=vec[i][1];j--){for(int k=target2;k>=vec[i][2];k--){dp[j][k]=max(dp[j][k],dp[j-vec[i][1]][k-vec[i][2]]+vec[i][0]);}}}return dp[target1][target2];
}
树状背包
买一件物品前必须买另一件
map键值是编号,first负重,second价值,买d[i][0]前必须买d[i][1],d[i][1]=0时表示没有依赖
思路,回溯思想自底向上遍历,每一层子树作为一个临时的商品组,根节点必须买,根节点买不了时更新为0
原理是把一棵树分为整合为前缀和组,实现起来保证每种情况更新到且在回溯前更新完即可
注意更新的数据所在的层级
int func7(unordered_map<int,pair<int,int>>&map,vector<vector<int>>&d,int target){int n=map.size();vector<vector<int>>tree(n+1);vector<vector<int>>dp(n+1,vector<int>(target+1));for(auto i:d){tree[i[1]].push_back(i[0]);}function<void(int)>dfs=[&](int root){for(int i=0;i<tree[root].size();i++){//遍历商品组int son=tree[root][i];dfs(son);for(int j=target-map[root].first;j>=map[son].first;j--){//商品组内不应该包含根节点,所以需要保留for(int k=0;k<=j;k++){//对商品的抽象,直接抽象为了对应的大小,不存在时为0dp[root][j]=max(dp[root][j],dp[root][j-k]+dp[son][k]);}}}for(int j=target;j>=map[root].first;j--)//根节点必须买 dp[root][j]=dp[root][j-map[root].first]+map[root].second;for(int j=0;j<map[root].first;j++) //根节点买不了的话gdp[root][j]=0;};dfs(0);return dp[0][target];
}
小数/分数背包,贪心
物品可以选择部分
vec[i][0]重量,vec[i][1]价值
int func8(vector<int>&vec,int target){sort(vec.begin(),vec.end(),[](vector<int>&v1,vector<int>&v2){return v1[1]*1.0/v1[0]>v2[1]*1.0/v2[0];});int value=0;for(int i=0;i<vec.size()&⌖i++){if(target>vec[i][0]){target-=vec[i][0];value+=vec[i][1];}else {value+=target*vec[i][1]*1.0/vec[i][0];target=0;}}return value;
}
泛化背包问题
没有固定代价和价值
int value(int index){...}
int weight(int index){...}
int func9(int size,int target){vector<int>dp(target+1,0);for(int i=0;i<size;i++){for(int w=target;w>=weight(i);w--){dp[w]=max(dp[w],dp[w-weight(i)]+value(i));}}return dp[target];
}
相关文章:
)
九种背包问题(C++)
0-1背包,背包大小target,占用容积vec[i][0],可以带来的利益是vec[i][1] 一件物品只能取一次,先遍历物品然后遍历背包更新不同容积下最大的利益 int func(vector<vector<int>>&vec,int target){vector<int>dp(target1,…...
008:安装Docker
安装Docker 如果不太熟悉Linux命令,不想学习Linux命令,可以直接看文末NAS面板章节,通过面板,像使用Window一样操作NAS。 一、安装 Docker 1.安装 Docker wget -qO- https://get.docker.com/ | sh2.启动 Docker 服务 sudo sys…...
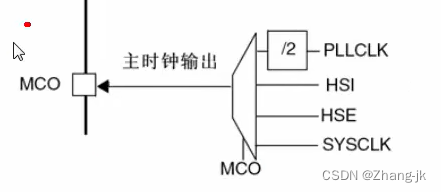
STM32第九节(中级篇):RCC(第一节)——时钟树讲解
目录 前言 STM32第九节(中级篇):RCC——时钟树讲解 时钟树主系统时钟讲解 HSE时钟 HSI时钟 锁相环时钟 系统时钟 SW位控制 HCLK时钟 PCLKI时钟 PCLK2时钟 RTC时钟 MCO时钟输出 6.2.7时钟安全系统(CSS) 小结 前言 从…...
Web核心,HTTP,tomcat,Servlet
1,JavaWeb技术栈 B/S架构:Browser/Server,浏览器/服务器架构模式,它的特点是,客户端只需要浏览器,应用程序的逻辑和数据都存储在服务器端。浏览器只需要请求服务器,获取Web资源,服务器把Web资源…...

空间(Space)概念:元素、集合、空间和数学对象
摘要: 在数学中,一个空间(Space)是一种特殊类型的数学对象。它通常是一个集合,但不仅仅是一个普通的集合,而是具有某种附加的结构和定义在其上的运算规则。这些额外的结构使得空间能够反映现实世界中的几何…...

【Datawhale组队学习:Sora原理与技术实战】训练一个 sora 模型的准备工作,video caption 和算力评估
训练 Sora 模型 在 Sora 的技术报告中,Sora 使用视频压缩网络将各种大小的视频压缩为潜在空间中的时空 patches sequence,然后使用 Diffusion Transformer 进行去噪,最后解码生成视频。 Open-Sora 在下图中总结了 Sora 可能使用的训练流程。…...
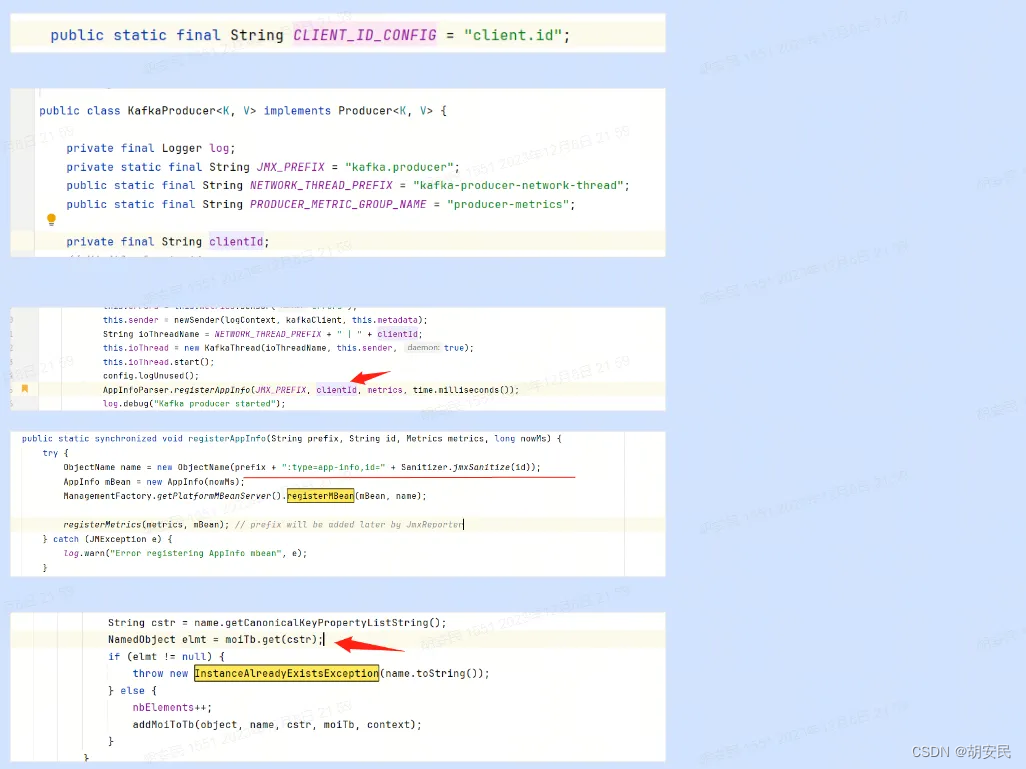
Kafka-生产者报错javax.management.InstanceAlreadyExistsException
生产者发送消息到 kafka 中,然后控制台报错 然后根据日志查看 kafka 的源码发现了问题原因 说的是MBean已经注册了,然后报异常了,这样就会导致生产者的kafka注册失败, 原因是项目上生产者没有配置clientId,默认都是空导致的, 多个生产者(项目)注册到kafka集群中的 id 都相同。 …...

Java常见问题:编辑tomcat运行环境、部署若伊系统
文章目录 引言I Eclipse1.1 编辑tomcat运行环境II JDK2.1 驱动程序无法通过使用安全套接字层(SSL)加密与 SQL Server 建立安全连接2.2 restriction on required library2.3 The type javax.servlet.http.HttpServletRequest cannot be resolved.的解决方法III npm3.1 npm报错:…...
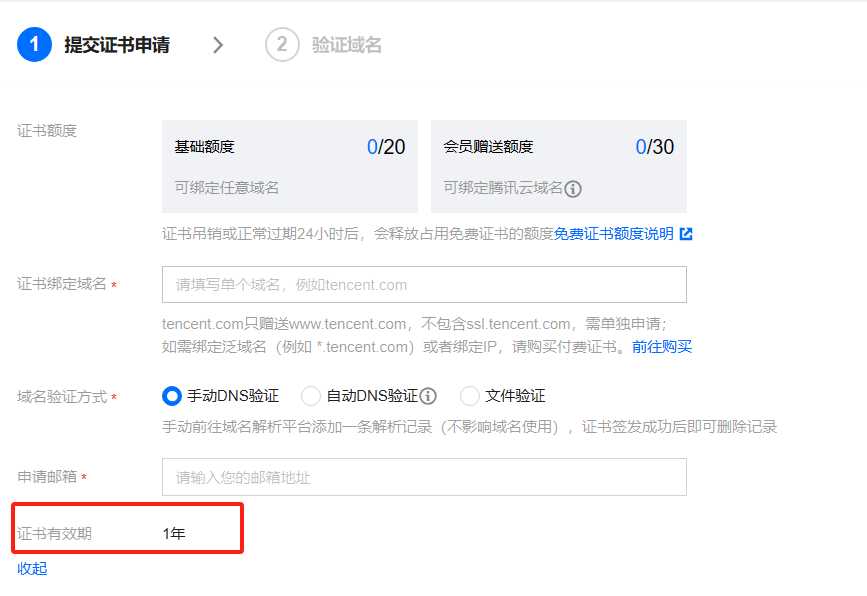
阿里云免费证书改为3个月,应对方法很简单
情商高点的说法是 Google 积极推进90天免费证书,各服务商积极响应。 情商低点的话,就是钱的问题。 现在基本各大服务商都在2024年停止签发1年期的免费SSL证书产品,有效期都缩短至3个月。 目前腾讯云倒还是一年期。 如果是一年期的话&#x…...

安装Pytorch——CPU版本
安装Pytorch——CPU版本 1. 打开pytorch官网2. 选择pip安装pytorch-cpu3.复制安装命令4. 在cmd命令窗口,进入你的虚拟环境4.1 创建虚拟环境4.2 进行安装 5. 安装成功6. 进行测试——如下面步骤,如图6.1 输入 python6.2 输入 import torch6.2 输入 print …...

MySQL中出现‘max_allowed_packet‘ variable.如何解决
默认情况下,MySQL的max_allowed_packet参数可能设置得相对较小,这对于大多数常规操作来说足够了。但是,当你尝试执行包含大量数据的操作(如大批量插入或大型查询)时,可能会超过这个限制,从而导致…...
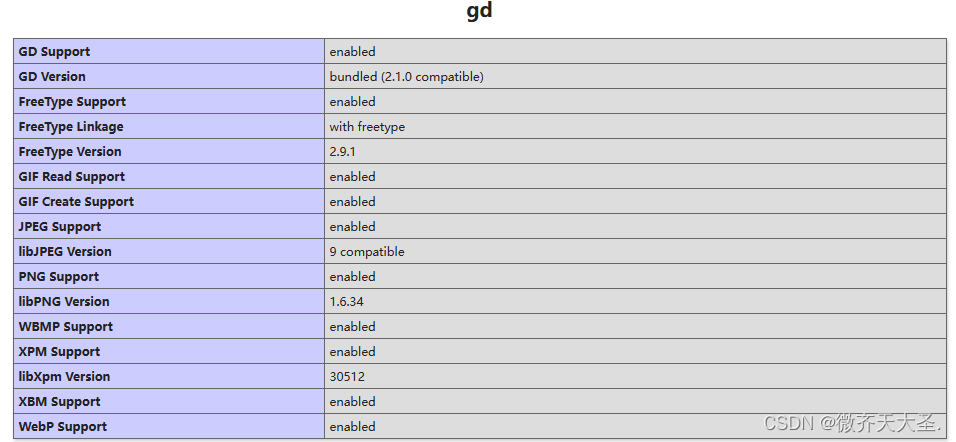
PHP 生成图片
1.先确认是否有GD库 echo phpinfo(); // 创建一个真彩色图像 $image imagecreatetruecolor(120, 50);// 分配颜色 $bgColor imagecolorallocate($image, 255, 255, 255); // 白色背景 $textColor imagecolorallocate($image, 230, 230, 230); // 黑色文字// 填充背景 image…...

【Spring Boot 3】【JSON】读取JSON文件
【Spring Boot 3】【JSON】读取JSON文件 背景介绍开发环境开发步骤及源码工程目录结构总结背景 软件开发是一门实践性科学,对大多数人来说,学习一种新技术不是一开始就去深究其原理,而是先从做出一个可工作的DEMO入手。但在我个人学习和工作经历中,每次学习新技术总是要花…...

网络学习:邻居发现协议NDP
目录 前言: 一、报文内容 二、地址解析----NS/NA 目标的被请求组播IP地址 邻居不可达性检测: 重复地址检测 路由器发现 地址自动配置 默认路由器优先级和路由信息发现 重定向 前言: 邻居发现协议NDP(Neighbor Discovery…...

Spring事务传播行为总结
事务传播行为介绍 Spring中的7个事务传播行为: 事务行为说明特点PROPAGATION_REQUIRED支持当前事务,假设当前没有事务。就新建一个事务父事务与子事务要么都成功,要么都失败PROPAGATION_SUPPORTS支持当前事务,假设当前没有事务࿰…...

AWTK slider_circle 控件发布
slider_circle 控件。 主要特色: 支持正向和反向支持设置滑块的半径支持背景线宽和颜色支持前景线宽和颜色支持设置是否显示值的文本支持设置起始角度和结束角度支持设置格式化值的格式字符串支持使用图片填充背景和前景 界面效果: 注意: …...

BitMap 和 HyperLogLog
目录 BitMap 常用命令 应用场景 日活统计 用户签到 HyperLogLog 什么是基数? 常用命令 应用场景 BitMap 问: "有10亿个不重复的无序的正数,如果快速排序?" 这看上去很简单,就是一个排序而已,但是大部分排序算…...

德人合科技 | 公司办公终端、电脑文件资料 \ 数据透明加密防泄密管理软件系统
天锐绿盾是一款全面的企业级数据安全解决方案,它专注于为企业办公终端、电脑文件资料提供数据透明加密防泄密管理。 首页 德人合科技——www.drhchina.com 这款软件系统的主要功能特点包括: 1. **透明加密技术**: 天锐绿盾采用了透明加密技…...

0基础 三个月掌握C语言(11)
字符函数和字符串函数 为了方便操作字符和字符串 C语言标准库中提供了一系列库函数 接下来我们学习一下这些函数 字符分类函数 C语言提供了一系列用于字符分类的函数,这些函数定义在ctype.h头文件中。这些函数通常用于检查字符是否属于特定的类别,例如…...
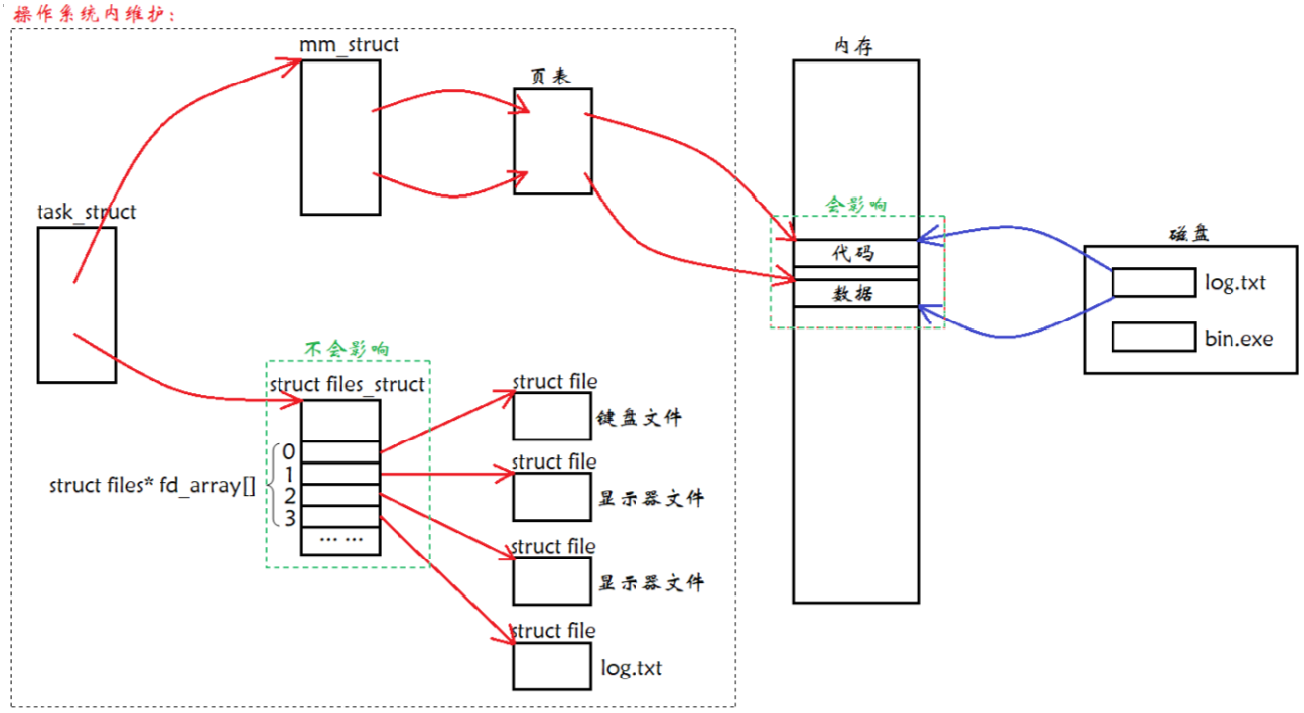
【Linux】基础 IO(文件描述符)-- 详解
一、前言 1、文件的宏观理解 文件在哪呢? 从广义上理解,键盘、显示器、网卡、声卡、显卡、磁盘等几乎所有的外设都可以称之为文件,因为 “Linux 下,一切皆文件”。 从狭义上的理解,文件在磁盘(硬件&#…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
