汇总全网免费API，持续更新（新闻api、每日一言api、音乐。。。）
Public&FreeAPI
网址：apis.whyta.cn （推荐）
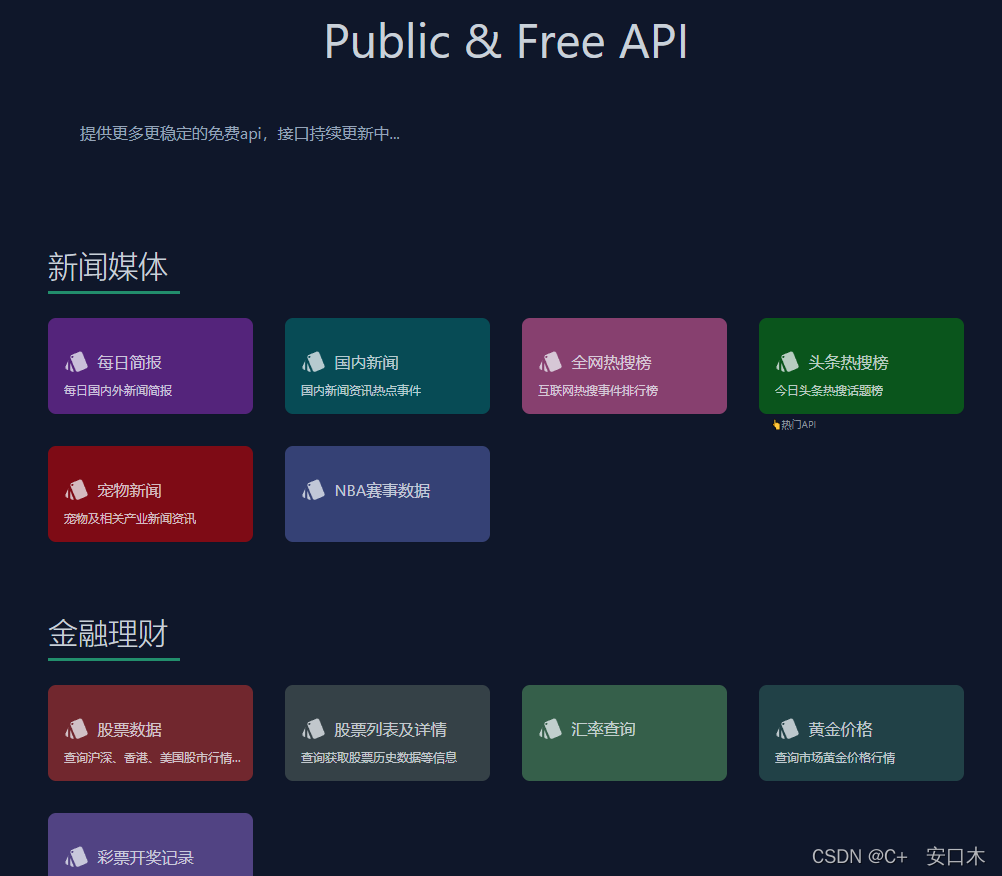
UomgAPI
网址：https://api.uomg.com
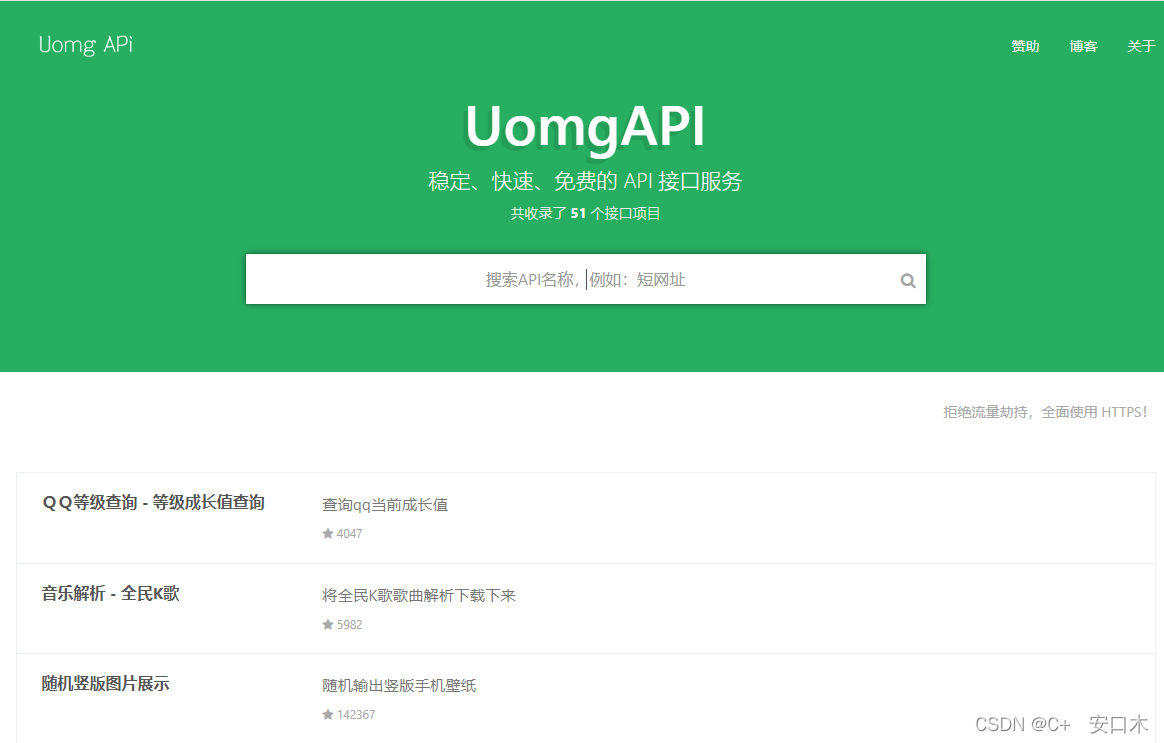
教书先生
网址：https://api.oioweb.cn/
山海API
https://api.shserve.cn/
云析API铺
https://api.a20safe.com/
韩小韩API
网址：https://api.vvhan.com
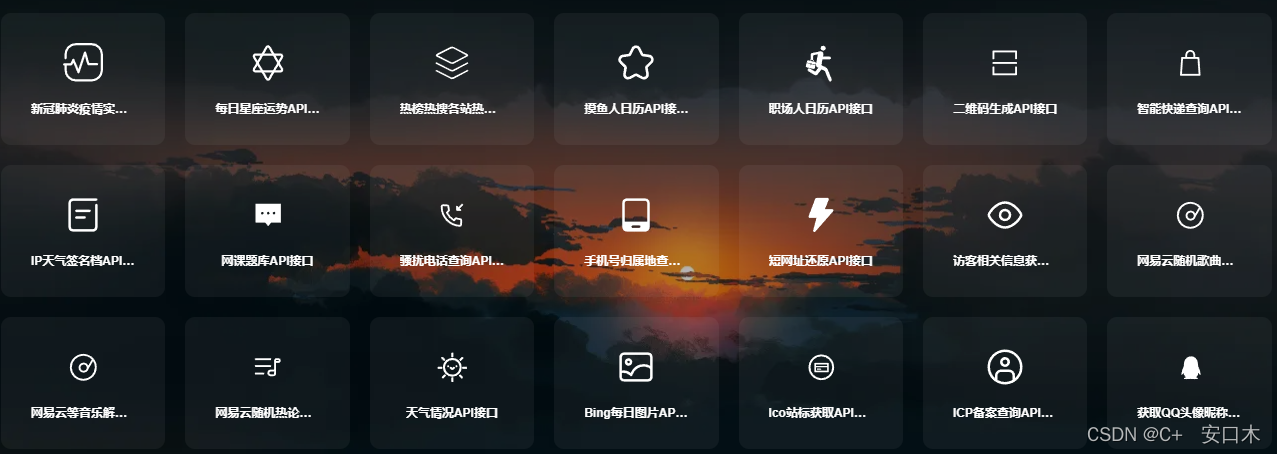
JSON API免费接口
各种提供JSON格式数据返回服务网站的API接口
http://www.bejson.com/knownjson/webInterface/
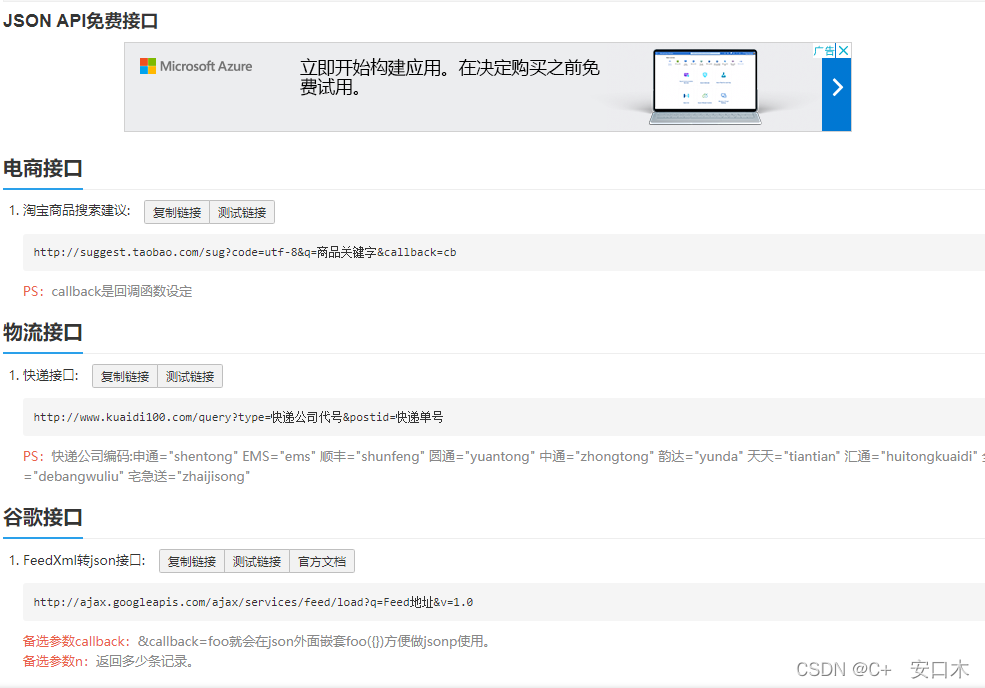
接口大全
网址：https://www.free-api.com
阿里云api市场
网址：https://market.aliyun.com/data
总结
如果需要更稳定的api，推荐大家使用付费api
欢迎大家提交免费 api 我们共同维护这篇文章
相关文章：
汇总全网免费API，持续更新（新闻api、每日一言api、音乐。。。）
Public&FreeAPI 网址：apis.whyta.cn （推荐） UomgAPI 网址：https://api.uomg.com 教书先生 网址：https://api.oioweb.cn/ 山海API https://api.shserve.cn/ 云析API铺 https://api.a20safe.com/ 韩小韩…...
Android SystemServer进程解析
SystemServer进程在android系统中占了举足轻重的地位，系统的所有服务和SystemUI都是由它启动。 一、SystemServer进程主函数流程 1、主函数三部曲 //frameworks/base/services/java/com/android/server/SystemServer.java /** * The main entry point from zy…...
Github主页设置贪吃蛇详细教程
先看最终实现结果： 有条贪吃蛇放在主页还是蛮酷的哈哈哈。接下来我来讲一讲怎么在Github主页添加一条贪吃蛇。 首先要修改自己的Github的主页，我们得有一个特殊的仓库——这个仓库必须与你的Github用户名保持一致，并且需要公开，…...
二、实现fastdfs文件上传与延迟删除功能的Spring Boot项目
如何在Spring Boot项目中集成FastDFS实现文件上传功能，并添加支持延迟删除功能的实现。 一、Spring Boot 中集成 fastdfs 使用 1、文件上传功能实现 首先，让我们看一下如何实现文件上传功能的接口方法： RestController public class File…...
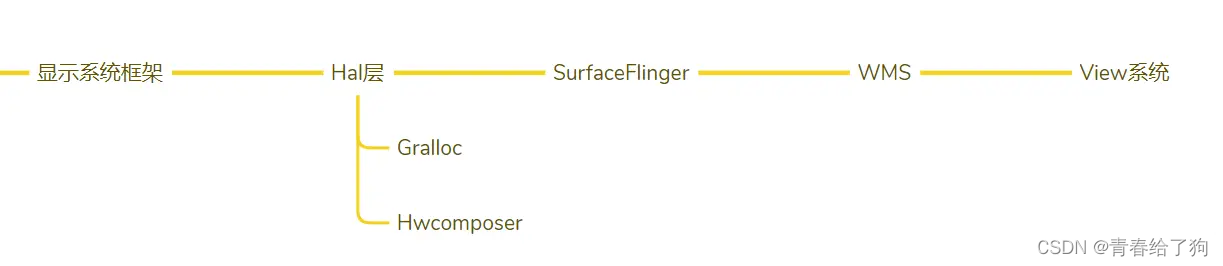
Android FrameWork 学习路线
目录 前言 学习路线： 1.基础知识 2、AOSP 源码学习 3. AOSP 源码编译系统 4. Hal与硬件服务 5.基础组件 6. Binder 7. 系统启动过程分析 8. 应用层框架编辑 9. 显示系统 10. Android 输入系统 11. 系统应用 前言 Android Framework 涉及的行业相当广…...
前端开发者如何打造自己的生态以及ip
作为独立开发者，在公司的岗位上面，经常面对的是页面，但我们不能局限页面，页面是切入点。 1在需求页面的过程中，我们会接触ui，原型，软件，需求， 2在接口对接的过程中&#…...
C语言实现一个两个数加减乘除的答题代码（含文件保存），用户增加，题目增加，题目测试，题目答题等等
目录 1、这是我大一自己写的小代码，现在翻到了就分享出来，高手勿喷。 2、项目运行 3、获取完整源码网址 1、这是我大一自己写的小代码，现在翻到了就分享出来，高手勿喷。 2、项目运行 （1）测试模块 每次…...
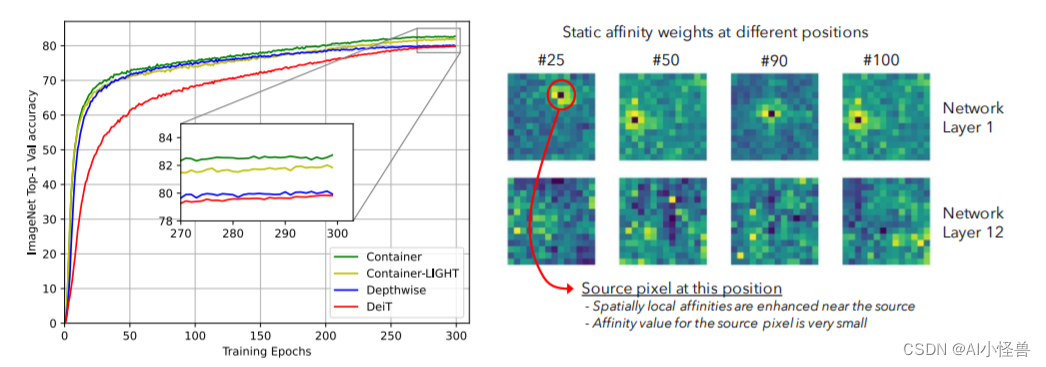
YOLOv9改进策略：注意力机制 | 用于微小目标检测的上下文增强和特征细化网络ContextAggregation，助力小目标检测，暴力涨点
💡💡💡本文改进内容：用于微小目标检测的上下文增强和特征细化网络ContextAggregation，助力小目标检测 yolov9-c-ContextAggregation summary: 971 layers, 51002153 parameters, 51002121 gradients, 238.9 GFLOPs 改…...
基于单片机的老人防丢系统设计
目 录 摘 要 I Abstract II 引 言 3 1 系统总体架构 6 1.1方案设计与选择 6 1.2 系统架构设计 6 1.3 系统器件选择 7 2 系统硬件设计 9 2.1 单片机外围电路设计 9 2.2 LCD1602液晶显示电路设计 12 2.3 短信模块电路设计 14 2.4 GPS模块电路设计 14 2.5 电源与按键控制电路设计…...
从海外开发者大会的亲身体悟聊起，谈谈 AI 与开发者关系的重构 | 编码人声
本期「编码人声」节目中，我们聚焦于「AI 与开发者关系的重构」这一主题，从嘉宾参加海外开发者大会的亲身体验开始分享，聊一聊 AI 技术如何影响开发者社区和生态，以及开发者如何在这一变革中找到新的位置。 我们邀请了开发者社区与…...
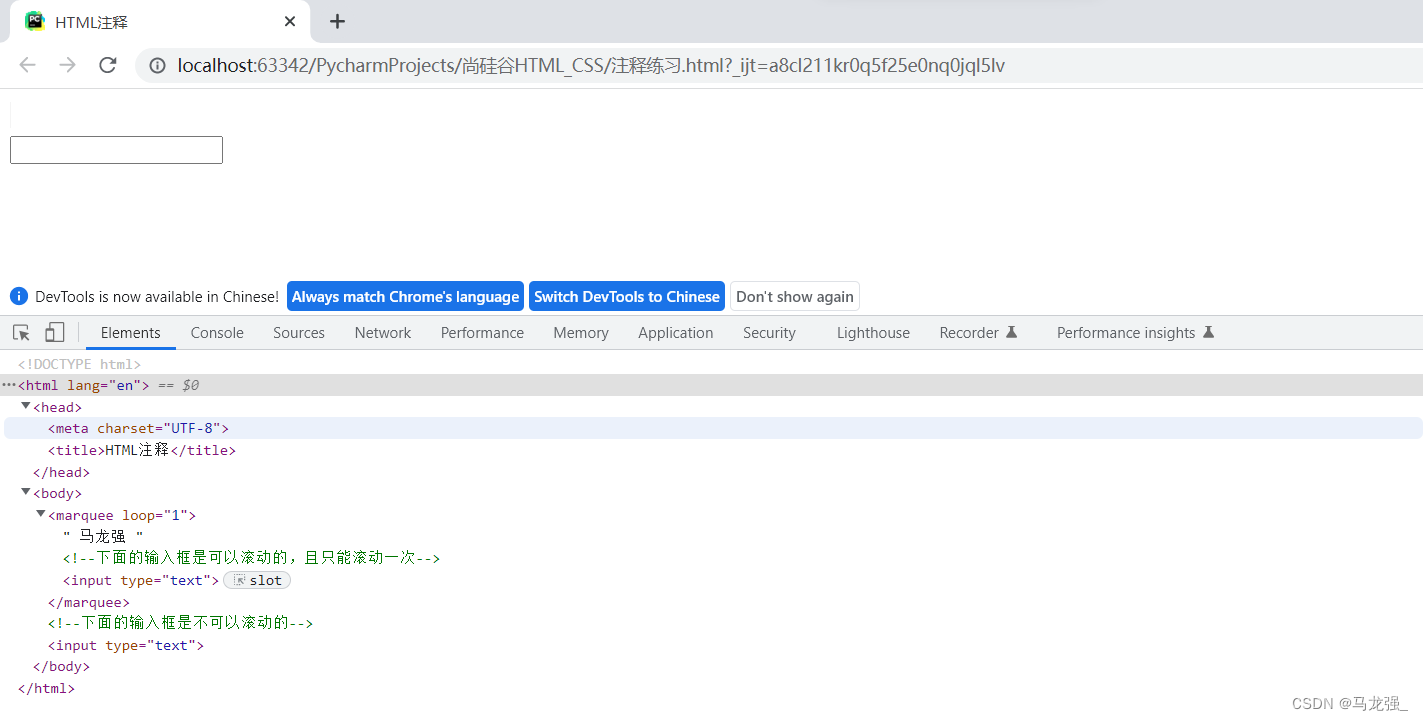
HTML_CSS练习：HTML注释
一、代码示例 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>HTML注释</title> </head> <body><marquee loop"1">马龙强<!--下面的输入框是可以滚动的&#x…...
面试官问我Java异步编程用过吗？我直接说了6种方式！
文章目录 线程池 Runnable/Callable线程池 FutureCompletableFuture线程池 Async注解Spring 事件创建事件事件发布者事件监听器调用事件 消息队列生产者消费者 在实际开发中有些耗时操作，或者对主流程不是那么重要的逻辑，可以通过异步的方式去执行&am…...
一维坐标的移动（bfs）
在一个长度为n的坐标轴上，小S想从A点移动B点。 他的移动规则如下： 向前一步，坐标增加1。 向后一步，坐标减少1。 跳跃一步，使得坐标乘2。 小S不能移动到坐标小于0或大于n的位置。 小S想知道从A点移动到B点的最少步数是多…...
面试题 整理
第1题：常见数据类型大小 这边以64位计算机系统，环境而言。 类型 存储大小 值范围 char 1 字节 -128 到 127 或 0 到 255 unsigned char 1 字节 0 到 255 signed char 1 字节 -128 到 127 int 4 字节 -32,768 到 32,767 或 -2,147,483,648…...
苍穹外卖-day08：导入地址簿功能代码（单表crud）、用户下单（业务逻辑）、订单支付（业务逻辑，cpolar软件）
苍穹外卖-day08 课程内容 导入地址簿功能代码用户下单订单支付 功能实现：用户下单、订单支付 用户下单效果图： 订单支付效果图： 1. 导入地址簿功能代码（单表crud） 1.1 需求分析和设计 1.1.1 产品原型（…...
Java面试相关问题
一.MySql篇 1优化相关问题 1.1.MySql中如何定位慢查询？ 慢查询的概念：在MySQL中，慢查询是指执行时间超过一定阈值的SQL语句。这个阈值是由long_query_time参数设定的，它的默认值是10秒1。也就是说，如果一条SQL语句的执…...
Linux Shell中的循环控制语句
Linux Shell中的循环控制语句 在编写Shell脚本时，循环是一种常用的控制结构，用于重复执行一系列命令。在Shell中，主要有三种循环控制语句：for循环，while循环，和until循环。 1. For循环 for循环是最常见的…...
proto3语言指南
Language Guide (proto3) 本指南介绍了如何使用 protocol buffer 语言来构建protocol buffer数据，包括.proto文件语法以及如何从.proto 文件生成数据访问类。它涵盖了proto3 版本的协议缓冲语言：有关proto2语法的信息，请参阅proto2语言指南。 文章目录 Language Guide (pro…...
解决后端传给前端的日期问题
解决方式： 1). 方式一 在属性上加上注解，对日期进行格式化 但这种方式，需要在每个时间属性上都要加上该注解，使用较麻烦，不能全局处理。 2). 方式二（推荐 ) 在WebMvcConfiguration中扩展SpringMVC的消息转…...
MySQL中的索引失效情况介绍
MySQL中的索引是提高查询性能的重要工具。然而，在某些情况下，索引可能无法发挥作用，甚至导致查询性能下降。在本教程中，我们将探讨MySQL中常见的索引失效情况，以及它们的特点和简单的例子。 1. **索引失效的情况** …...
.Net框架，除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...
使用van-uploader 的UI组件，结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui（适配 Vue2 版本 ）实现截图中照片上传预览、删除功能，并封装成可复用组件的完整代码，包含样式和逻辑实现，可直接在 Vue2 项目中使用： 1. 封装的图片上传组件 ImageUploader.vue <te…...
代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中，常常会遇到 跨域请求接口 的情况。为了解决这个问题，Vite 和 Webpack 都提供了 proxy 代理功能，用于将本地开发请求转发到后端服务器。 什么是代理（proxy）？ 代理是在开发过程中，前端项目通过开发服务器，将指定的请求“转发”到真实的后端服务器，从而绕…...
CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值，用于设置元素的宽度根据其内容自动调整，确保宽度刚好容纳内容而不会超出。 效果对比 默认情况（width: auto）： 块级元素（如 <div>）会占满父容器…...
【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT，橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版：职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
Git常用命令完全指南：从入门到精通
Git常用命令完全指南：从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
elementUI点击浏览table所选行数据查看文档
项目场景： table按照要求特定的数据变成按钮可以点击 解决方案： <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中，压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言，提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
DiscuzX3.5发帖json api
参考文章：PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下，适配我自己的需求 有一个站点存在多个采集站，我想通过主站拿标题，采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
阿里云Ubuntu 22.04 64位搭建Flask流程（亲测）
cd /home 进入home盘 安装虚拟环境： 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境： virtualenv myenv 3、激活虚拟环境（激活环境可以在当前环境下安装包） source myenv/bin/activate 此时，终端…...