堆(数据结构)

堆的概念及结构
如果有一个关键码的集合K = { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足: <= 且 <= ( >= 且 >= ) i = 0,1,2…,则称为小堆(或大堆)。
将根节点最大的堆叫做最大堆或大根堆,
节点最小的堆叫做最小堆或小根堆。
堆的性质:
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。

1.下列关键字序列为堆的是:()
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32
2.已知小根堆为8,15,10,21,34,16,12,删除关键字 8 之后需重建堆,在此过程中,关键字之间的比较次数是()。
A 1
B 2
C 3
D 4
3.一组记录排序码为(5 11 7 2 3 17),则利用堆排序方法建立的初始堆为
A(11 5 7 2 3 17)
B(11 5 7 2 17 3)
C(17 11 7 2 3 5)
D(17 11 7 5 3 2)
E(17 7 11 3 5 2)
F(17 7 11 3 2 5)
4.最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后,其结果是()
A[3,2,5,7,4,6,8]
B[2,3,5,7,4,6,8]
C[2,3,4,5,7,8,6]
D[2,3,4,5,6,7,8]
选择题答案:
1.A
2.C
3.C
4.C
堆的实现
1 堆向下调整算法
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
int array[] = {27,15,19,18,28,34,65,49,25,37};
堆的创建
下面我们给出一个数组,这个数组逻辑上可以看做一颗完全二叉树,但是还不是一个堆,现在我们通过算法,把它构建成一个堆。根节点左右子树不是堆,我们怎么调整呢?
在此我们有两种建堆方法:
1. 利用向上调整的方法,从第2 个节点开始一直调整到最后,就可以调整成堆。
2. 利用向下调整的方法,我们从倒数的第一个非叶子节点的子树开始调整,一直调整到根节点的树,就可以调整成堆。
但是第一种建堆的时间复杂度为 O(N*logN),第二种建堆的时间复杂度为O(N)
所以我们在此用第二种方法。

堆的插入
先插入一个10到数组的尾上,再进行向上调整算法,直到满足堆。

堆的删除
删除堆是删除堆顶的数据,将堆顶的数据根最后一个数据一换,然后删除数组最后一个数据,再进行向下调整算法。

堆的代码实现
Heap.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
#include<string.h>typedef int HeapDataType;
typedef struct Heap
{HeapDataType* a;int size;int capacity;
}Heap;void HeapInit(Heap* ph);void HeapInitArray(HeapDataType* a, Heap* ph,int n);
void HeapDestroy(Heap* ph);
void HeapPush(Heap* ph, HeapDataType x);
void HeapPop(Heap* ph);
HeapDataType HeapTop(Heap* ph);
void AdjustUp(HeapDataType* a, int child);
void AdjustDown(HeapDataType* pa, int n, int parent);
bool HeapEmpty(Heap* ph);Heap.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"void HeapInit(Heap* ph)
{assert(ph);ph->a = NULL;ph->size = 0;ph->capacity = 0;
}
void HeapDestroy(Heap* ph)
{assert(ph);ph->size = 0;ph->capacity = 0;free(ph->a);ph->a = NULL;
}//利用其它数组数据,建造一个堆存储数据
void HeapInitArray(Heap* ph,HeapDataType* a, int n)
{assert(ph);HeapDataType* tmp = (HeapDataType*)malloc(sizeof(HeapDataType) * n);if (tmp == NULL){perror("malloc fail!");exit(-1);}ph->a = tmp;ph->size = ph->capacity = n;memcpy(ph->a , a , n*sizeof(HeapDataType));//向上调整建堆,时间复杂度O(N*logN)//for (int i = 1; i < ph->size; i++)//{// AdjustUp(ph->a,i);//}//向下调整建堆,从第一个不为叶子的节点,时间复杂度O(N)for(int i = (ph->size - 1 - 1)/2; i >= 0; i--){AdjustDown(ph->a,n,i);}
}void Swap(HeapDataType*p1, HeapDataType*p2)
{HeapDataType tmp=*p1;*p1 = *p2;*p2 = tmp;
}void AdjustDown(HeapDataType* a,int n , int parent)
{int child = parent*2 + 1;while (child < n){if (child + 1<n && a[child + 1] < a[child]){child++;}if (a[parent] > a[child]){Swap(&a[parent],&a[child]);parent = child;child = parent * 2 +1;}else{break;}}
}
//建造小堆
void AdjustUp(HeapDataType* a, int child)
{int parent = (child - 1) / 2;//while(parent>=0)while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
void HeapPush(Heap* ph, HeapDataType x)
{assert(ph);if (ph->size == ph->capacity){int newcapacity = ph->capacity == 0 ? 4 : ph->capacity * 2;HeapDataType* tmp=(HeapDataType*)realloc(ph->a,newcapacity*sizeof(HeapDataType));if (tmp == NULL){perror("realloc fail!");exit(-1);}ph->a = tmp;ph->capacity = newcapacity;}ph->size++;ph->a[ph->size - 1] = x;AdjustUp(ph->a, ph->size - 1);
}
void HeapPop(Heap* ph)
{assert(ph);//必须有数据assert(ph->size);Swap(&ph->a[0], &ph->a[ph->size - 1]);ph->size--;AdjustDown(ph->a,ph->size,0);}
HeapDataType HeapTop(Heap* ph)
{assert(ph);return ph->a[0];
}
bool HeapEmpty(Heap* ph)
{assert(ph);return ph->size == 0;
}Test.c
#include"Heap.h"
int main()
{//Heap heap1;//HeapInit(&heap1);//HeapPush(&heap1,1);//HeapPush(&heap1,54);//HeapPush(&heap1,48);//HeapPush(&heap1,48);//HeapPush(&heap1,15);//HeapPush(&heap1,35);//int a []={21,54,87,64,87,15};//Heap heap2;//HeapInit(&heap2);//for (int i = 0; i < (sizeof(a)/sizeof(int)); i++)//{// HeapPush(&heap2, a[i]);//}//while (!HeapEmpty(&heap2))//{// printf("%d\n", HeapTop(&heap2));// HeapPop(&heap2);//}//int a[] = { 21,54,87,64,87,15 };//Heap heap2;//HeapInitArray(&heap2 ,a,sizeof(a)/sizeof(HeapDataType));//建立了小堆//HeapDestroy(&heap2);return 0;
}
这个博客如果对你有帮助,给博主一个免费的点赞就是最大的帮助❤
欢迎各位点赞,收藏和关注哦❤
如果有疑问或有不同见解,欢迎在评论区留言哦❤
后续我会一直分享双一流211西北大学软件(C,数据结构,C++,Linux,MySQL)的学习干货以及重要代码的分享
相关文章:

堆(数据结构)
堆的概念及结构 如果有一个关键码的集合K { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足: < 且 < ( > 且 > ) i 0,1ÿ…...

医药工厂5G智能制造数字孪生可视化平台,推进医药企业数字化转型
医药工厂5G智能制造数字孪生可视化平台,推进医药企业数字化转型。随着科技的不断发展,数字化转型已成为医药企业不可或缺的一部分。5G智能制造医药工厂数字孪生可视化平台作为数字化转型的重要工具,正在逐步改变医药企业的生产方式和管理模式…...
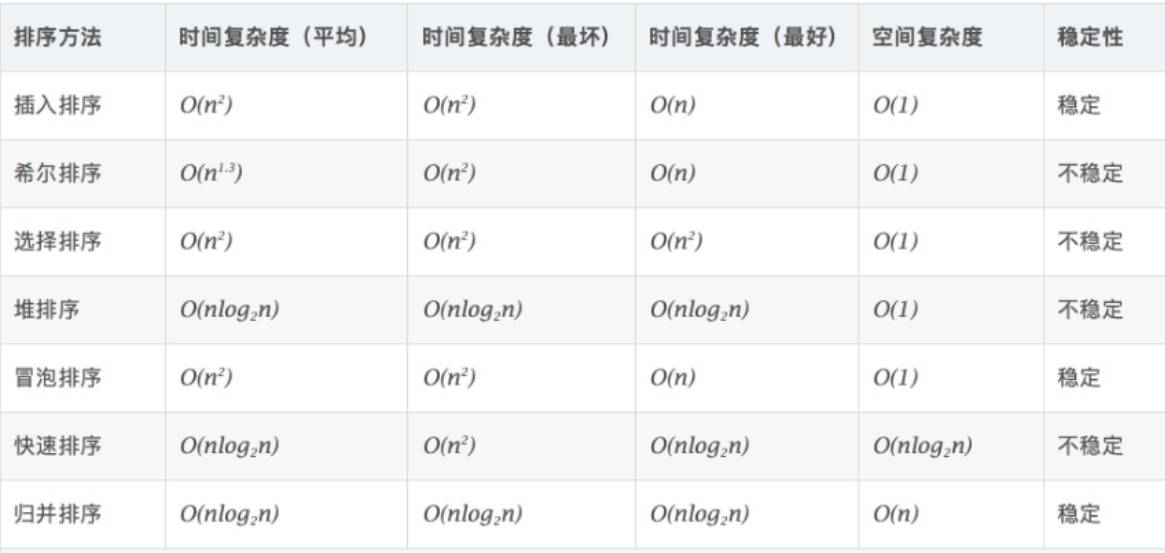
C语言学习--八种排序算法
目录 排序的概念 1.直接插入排序 基本思想 代码实现 算法分析 2.希尔排序 基本思想 代码实现 算法分析 3.冒泡排序 基本思想 代码实现 算法分析 4.快速排序 基本思想 代码实现 算法分析 5.简单选择排序 基本思想 代码实现 算法分析 6.堆排序 基本思想 代…...
Infineon_TC264智能车代码初探及C语言深度学习(二)
本篇文章记录我在智能车竞赛中,对 Infineon_TC264 这款芯片的底层库函数的学习分析。通过深入地对其库函数进行分析,C语言深入的知识得以再次在编程中呈现和运用。故觉得很有必要在此进行记录分享一下。 目录 编辑 一、代码段分析 NO.1 指向结构体…...

第十三届蓝桥杯(C/C++ 大学B组)
目录 试题 A: 九进制转十进制 试题 B: 顺子日期 试题 C: 刷题统计 试题 D: 修剪灌木 试题 E: X 进制减法 试题 F: 统计子矩阵 试题 G: 积木画 试题 H: 扫雷 试题 I: 李白打酒加强版 试题 J: 砍竹子 试题 A: 九进制转十进制 九进制正整数 ( 2022 )转换成十进制等于多…...
数据结构从入门到精通——排序的概念及运用
排序的概念及运用 前言一、排序的概念排序稳定性内部排序外部排序 二、排序运用三、常见的排序算法四、排序性能检测代码srand()clock() 五、oj排序测试代码 前言 排序是将数据按照一定规则重新排列的过程,常见规则有升序、降序等。排序算法如冒泡排序、快速排序等…...
react面试题总结
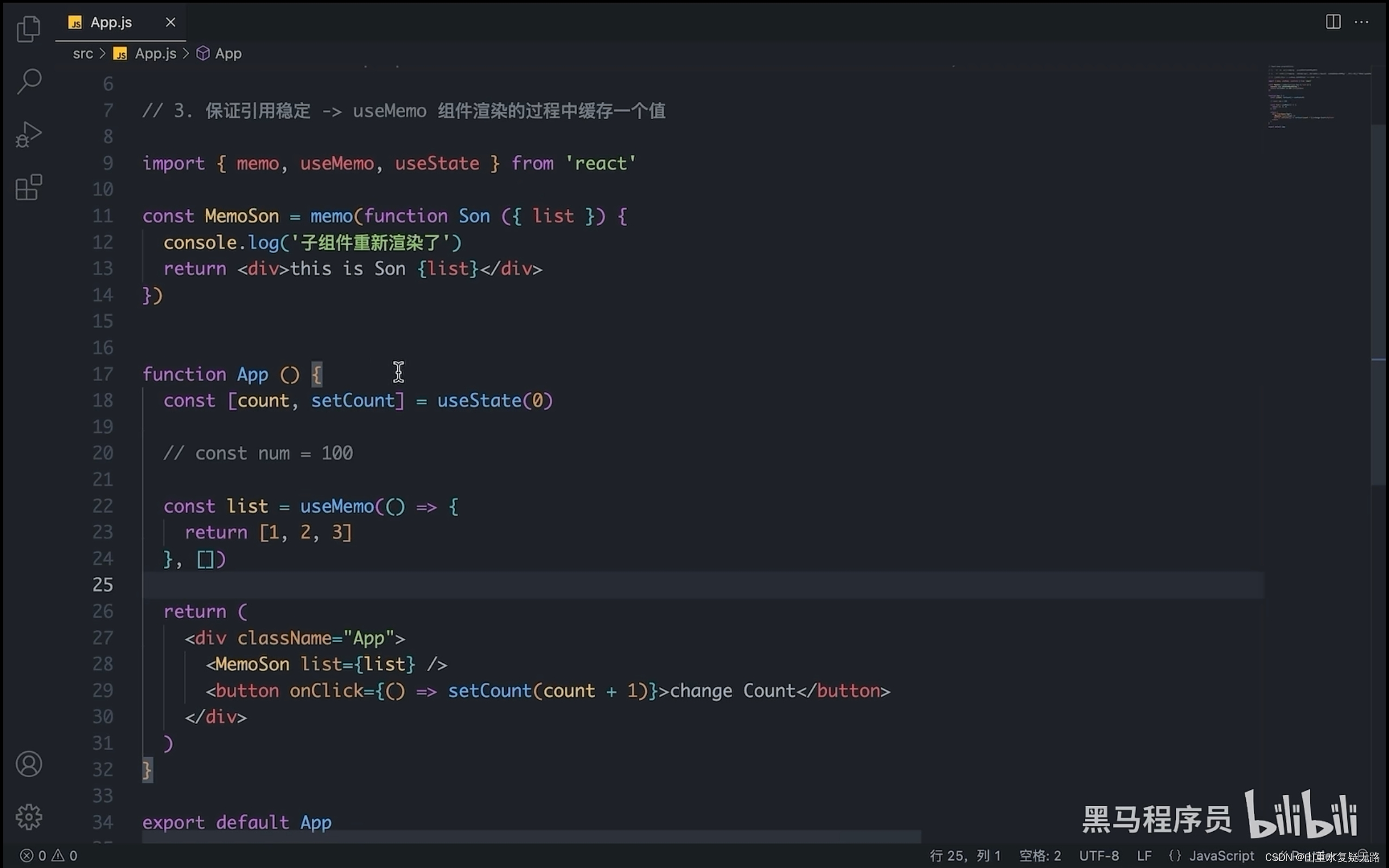
1、当调用 setState的时候,发生了什么操作? 当调用 setState时, React做的第一件事是将传递给setState的对象合并到组件的当前状态,这将启动一个称为和解( reconciliation)的过程。 和解的最终目标是&#…...
5_springboot_shiro_jwt_多端认证鉴权_禁用Cookie
1. Cookie是什么 Cookie是一种在客户端(通常是用户的Web浏览器)和服务器之间进行状态管理的技术。当用户访问Web服务器时,服务器可以向用户的浏览器发送一个名为Cookie的小数据块。浏览器会将这个Cookie存储在客户端,为这个Co…...

条形码申请指南:外地人如何成功注册香港条形码
香港条形码是打造的通行证,消费者对香港条码有一定的认知,拥有香港条形码就获得消费者对产品的认可,香港条形码是全球条码中具有防伪功能的条形码,化妆品、护肤品、保健品、包装食品等行业的产品认证,就有必要申请香港…...

Covalent Network借助大规模的历史Web3数据集,推动人工智能发展
人工智能在众多领域中增强了区块链的实用性,反之亦然,区块链确保了 AI 模型所使用的数据的来源和质量。人工智能带来的生产力提升,将与区块链系统固有的安全性和透明度融合。 Covalent Network(CQT)正位于这两项互补技…...

test测试类-变量学习
test测试类 作用:标记到类上成为测试类,标记到方法上成为测试方法 变量:测试类的变量,在测试类括号中应用 1、invocationCount变量 意思是这个方法应该被调用的次数。 在测试框架中,特别是当使用参数化测试或数据驱动…...

【DL经典回顾】激活函数大汇总(二十七)(Bent Identity附代码和详细公式)
激活函数大汇总(二十七)(Bent Identity附代码和详细公式) 更多激活函数见激活函数大汇总列表 一、引言 欢迎来到我们深入探索神经网络核心组成部分——激活函数的系列博客。在人工智能的世界里,激活函数扮演着不可或…...

element-plus el-table表格默认选中某一行
需求:进入页面时默认选中表格第一行 <el-tableref"singleTableRef":data"tableData"highlight-current-rowrow-click"handleCurrentChange" ><el-table-column property"date" label"日期" /><…...

Vue+SpringBoot打造民宿预定管理系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 用例设计2.2 功能设计2.2.1 租客角色2.2.2 房主角色2.2.3 系统管理员角色 三、系统展示四、核心代码4.1 查询民宿4.2 新增民宿4.3 新增民宿评价4.4 查询留言4.5 新增民宿订单 五、免责说明 一、摘要 1.1 项目介绍 基于…...
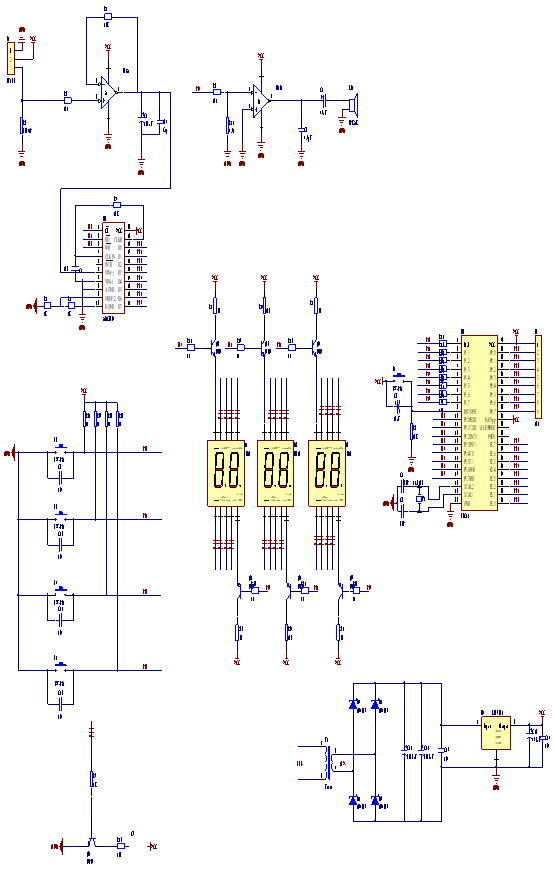
基于单片机的模糊PID炉温控制系统设计
摘 要 电热炉是在工业热处理的生产中广泛使用的一种设备,电热炉的温度控制系统存在时变性,非线性,滞后性等特征,难以用常规PID的控制器对系统达到很好的控制效果。当控温精度的要求高时,使用传统的控制理论方法难以达…...

深入浅出落地应用分析:AI数字人「微软小冰」
hi,各位,今天要聊的是AI小冰,机缘巧合,投递了这家公司的产品,正好最近在看数字人相关的,就详细剖析下这款产品! 前言 小冰,全称为北京红棉小冰科技有限公司,前身为微软(亚洲)互联网工程院人工智能小冰团队,是微软全球最大的人工智能独立产品研发团队。作为微软全…...

【早鸟优惠|高录用|EI稳定检索】2024年虚拟现实、图像和信号处理国际学术会议(ICVISP 2024)诚邀投稿/参会!
【早鸟优惠|高录用|EI稳定检索】 2024年虚拟现实、图像和信号处理国际学术会议(ICVISP 2024)诚邀投稿/参会! # 早鸟优惠 # 先投稿先送审 # #投稿免费参会、口头汇报及海报展示# 2024年虚拟现实、图像和信号处理国际学术会议(I…...

CPU设计实战—异常处理指令
异常类型以及精确异常的处理 异常有点像中断,处理完还要回到原来的状态,所以需要对之前的状态进行保存。本CPU主要实现对以下异常的处理: 1.外部硬件中断 2.复位异常 3.系统调用异常(发生在译码阶段) 4.溢出异常&…...
 match_phrase的使用)
Elasticsearch(13) match_phrase的使用
elasticsearch version: 7.10.1 match_phrase 语法 POST <index>/_search {"query": {"match_phrase": {"<field_name>": {"query": "<your_search_phrase>","slop": <max_dis…...

通过路由器监控,优化网络效率
路由器是网络的基本连接组件,路由器监控涉及将路由器网络作为一个整体进行管理,其中持续监控路由器的性能、运行状况、安全性和可用性,以确保更好的操作和最短的停机时间,因此监控路由器至关重要。 为什么路由器监控对组织很重要…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

