【亲测】Onlyfans年龄认证怎么办?Onlyfans需要年龄验证?
1. 引言
- 什么是OnlyFans:OnlyFans是一种内容订阅服务,成立于2016年,允许内容创作者从用户那里获得资金,用户需要支付订阅费用才能查看他们的内容。它在多个领域受到欢迎,包括音乐、健身、摄影,以及成人内容创作。
- OnlyFans是一款国外的私人性质的社交软件,也是一个付费会员平台。它主要提供给创作者、艺人、模特等有粉丝的人士使用,允许他们在平台上发布照片、视频、文字等内容,并设定不同的订阅价格。只有付费订阅了他们的账号,粉丝才能够看到这些独家内容,同时创作者也能通过粉丝的订阅获得收入。因此,OnlyFans也被称为“付费社交”。
但是OnlyFans对于订阅用户有着严格年龄限制,很多朋友不知道怎么通过年龄限制。本教程旨在帮助大家如何在OnlyFans上通过年龄验证。
2. 为什么会有年龄验证?
OnlyFans实施年龄验证的原因主要是为了遵守法律法规,保护未成年人免受不适宜内容的影响。
由于OnlyFans允许创作者发布各种内容,因此必须确保使用者已达到法定年龄,以合法浏览这些内容。
这种措施有助于平台创建一个安全的环境,既保护了用户,也遵守了各国关于网络内容和未成年人保护的法律要求。
年龄验证是OnlyFans为确保其内容不被未成年人访问而采取的一种预防措施,通过这种方式,OnlyFans试图平衡用户自由与社会责任。
3. OnlyFans的年龄验证方式
从注册流程来看,注册OnlyFans的时候只需要提供邮箱,并没有要求输入年龄。
进入OnlyFans后,在设置界面中也并没有找到设置年龄的地方。
因此,OnlyFans是通过third-part来验证用户年龄的。
4. 如何通过年龄验证?
考虑到OnlyFans主要通过以下几种方式验证年龄:
- 注册时使用的邮箱
- 订阅使用的信用卡
- 登陆环境
所以,可以从下面三个角度来进行验证
4.1 使用虚拟visa注册
这个是影响年龄验证的一个比较重要的因素。
因为订阅时使用的信用卡也可以用作年龄验证,所以信用卡也需要更改。
这里推荐使用wildcard,从链接进入有两美元的开卡优惠。
具体开卡教程可以参考这篇文章:订阅OnlyFans攻略-CSDN博客
4.2 修改邮箱年龄
进入你的邮箱设置界面,将生日信息设置为成年的出生年月。google邮箱设置界面如下,其他邮箱也是同理。

4.3 使用代理切换IP
有同学表示,OnlyFans出现年龄验证时,切换IP也是有效的。
虽然并不知道什么原理,但是如果大家前两条都没用的话,可以试一下这个方法。
5. 总结
通过年龄验证主要有以下几种方式:通过使用虚拟信用卡注册(通过本链接注册可优惠2美元年费)、调整邮箱中的生日信息,以及在必要时切换IP地址,用户可以有效地满足OnlyFans的年龄验证要求。需注意的是,平台有可能更改年龄验证规则,以上方式并不能保证一直有效,因此请先确认规则。
通过年龄验证后,就可以开始愉快的订阅啦~

相关文章:

【亲测】Onlyfans年龄认证怎么办?Onlyfans需要年龄验证?
1. 引言 什么是OnlyFans:OnlyFans是一种内容订阅服务,成立于2016年,允许内容创作者从用户那里获得资金,用户需要支付订阅费用才能查看他们的内容。它在多个领域受到欢迎,包括音乐、健身、摄影,以及成人内容…...

ASP.NET Core新特性
1. ASP.NET Core2.1 ASP.NET Core 2.1于2018年5月30日发布。是ASP.NET Core框架的一个重要版本,带来了许多新功能和改进。以下是ASP.NET Core 2.1中一些主要的特性: SignalR:引入了 SignalR,这是一个实时通信库,使得构…...
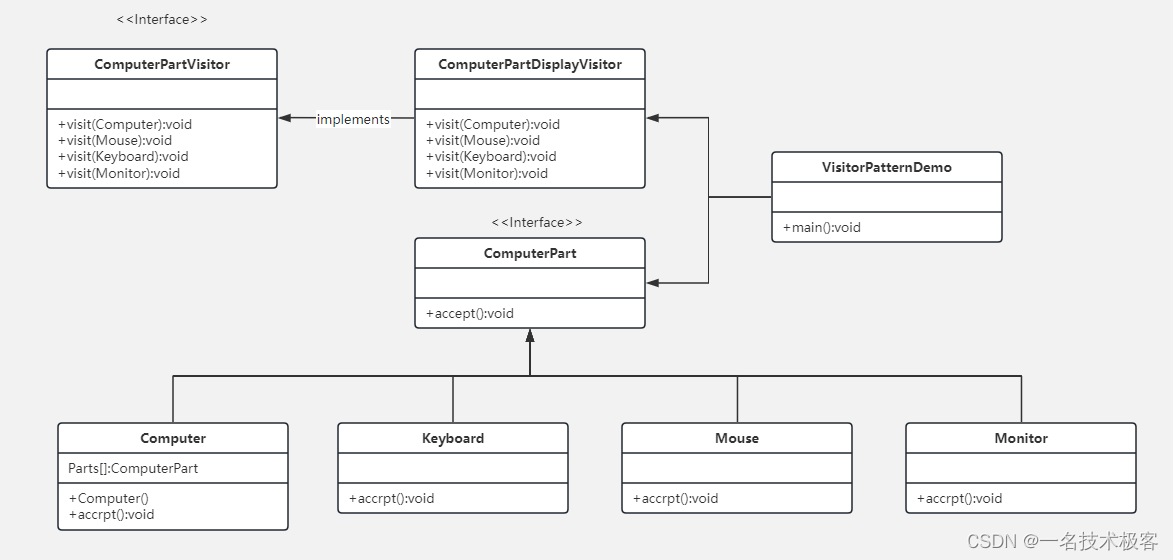
26-Java访问者模式 ( Visitor Pattern )
Java访问者模式 摘要实现范例 访问者模式(Visitor Pattern)使用了一个访问者类,它改变了元素类的执行算法,通过这种方式,元素的执行算法可以随着访问者改变而改变访问者模式中,元素对象已接受访问者对象&a…...
电子科技大学链时代工作室招新题C语言部分---题号G
1. 题目 问题的第一段也是非常逆天,说实话,你编不出问题背景可以不编。 这道题的大概意思就是, Pia要去坐飞机,那么行李就有限重。这时Pia想到自己带了个硬盘,众所周知,硬盘上存储的数据就是0和1的二进制序…...
体育运动直播中的智能运动跟踪和动作识别系统 - 视频分析如何协助流媒体做出实时决策
AI-Powered Streaming Vision: Transforming Real-Time Decisions with Video Analytics 原著:弗朗西斯科冈萨雷斯|斯特朗(STRONG)公司首席ML科学家 翻译:数字化营销工兵 实时视频分析通过即时处理实时视频数据&…...

Avalon总线学习
Avalon总线学习 avalon总线可以分为: Avalon clock interface Avalon reset interface Avalon Memory mapped interface Avalon iterrupt interface Avalon streaming interface Avalon tri-state conduit interface Avalon conduit interface 1、Avalon c…...
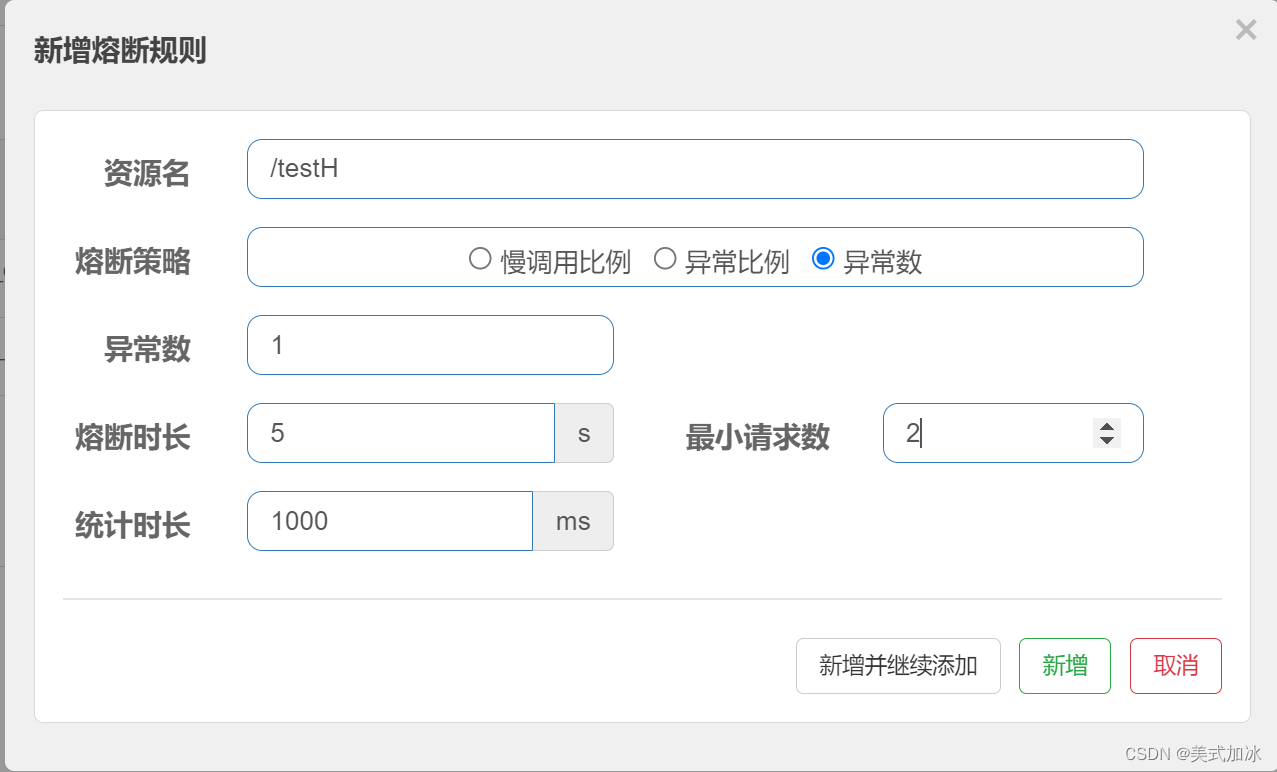
Sentinel(熔断规则)
慢调用比例 慢调用比例( SLOM_REQUEST_RATTo ):选择以慢调用比例作为阈值,需要设置允许的慢调用RT(即最大的响应时间),请求的响应时间大于该值则统计为慢调用。当单位统计时长(statIntervalMs)内请求数目大于设置的最小请求数目,…...

Hive借助java反射解决User-agent编码乱码问题
一、需求背景 在截取到浏览器user-agent,并想保存入数据库中,经查询发现展示的为编码后的结果。 现需要经过url解码过程,将解码后的结果保存进数据库,那么有几种实现方式。 二、问题解决 1、百度:url在线解码工具 …...
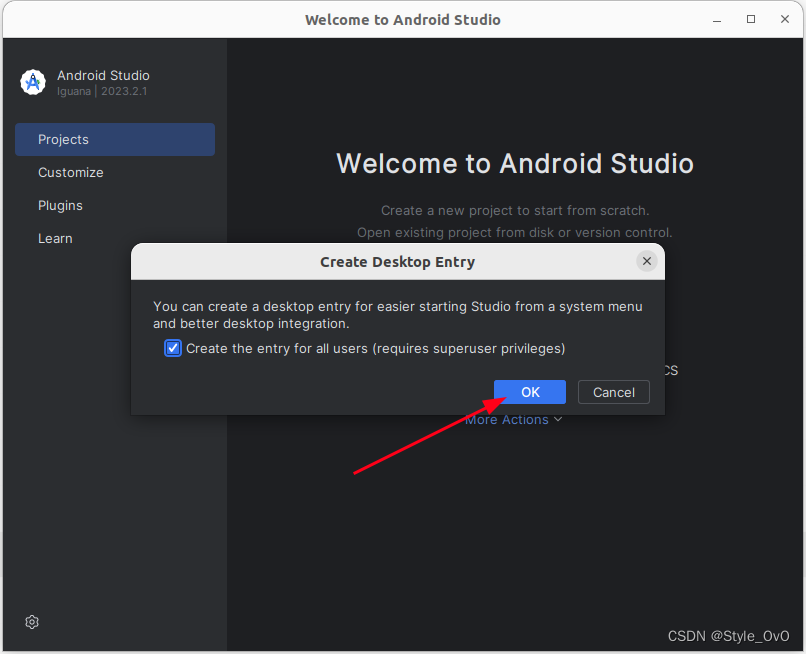
Linux下安装Android Studio及创建桌面快捷方式
下载 官网地址:https://developer.android.com/studio?hlzh-cn点击下载最新版本即可 安装 将下载完成后文件,进行解压,然后进入android-studio-2023.2.1.23-linux/android-studio/bin目录下,启动studio.sh即可为了更加方便的使…...
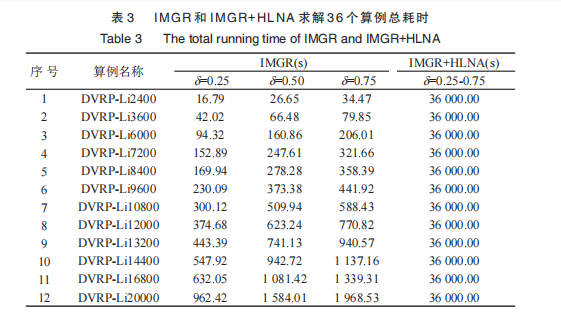
【析】一类动态车辆路径问题模型和两阶段算法
一类动态车辆路径问题模型和两阶段算法 摘要 针对一类动态车辆路径问题,分析4种主要类型动态信息对传统车辆路径问题的本质影响,将动态车辆路径问题(Dynamic Vehicle Routing Problem, DVRP)转化为多个静态的多车型开放式车辆路径问题(The Fleet Size a…...

从基础入门到学穿C++
前言知识 C简介 C是一门什么样的语言,它与C语言有着什么样的关系? C语言是结构化和模块化的语言,适合处理较小规模的程序。对于复杂的问题,规模较大的程序,需要高度的抽象和建模时,C语言则不合适。为了解…...

代码随想录算法训练营第二十四天|leetcode78、90、93题
一、leetcode第93题 class Solution { public:vector<string> restoreIpAddresses(string s) {int n s.size();vector<string> res;function<void(string, int, int)> dfs [&](string ss, int idx, int t) -> void {// 终止条件,枚举完&…...

Java学习笔记NO.20
Java流程控制 1. 用户交互 Scanner Java中的Scanner类用于获取用户输入,可以从标准输入(键盘)读取各种类型的数据。 import java.util.Scanner; public class UserInputExample { public static void main(String[] args) { Scanner sc…...

关系型数据库mysql(1)基础认知和安装
目录 一.数据库的基本概念 1.1数据 1.2表 1.3数据库 1.4 DBMS 数据库管理系统 1.4.1基本功能 1.4.2优点 1.4.3DBMS的工作模式 二.数据库的发展历史 2.1发展的三个阶段 第一代数据库 第二代数据库 第三代数据库 2.2mysql发展历史 三.主流数据库 四.关系型数据库和…...
WanAndroid(鸿蒙版)开发的第三篇
前言 DevEco Studio版本:4.0.0.600 WanAndroid的API链接:玩Android 开放API-玩Android - wanandroid.com 其他篇文章参考: 1、WanAndroid(鸿蒙版)开发的第一篇 2、WanAndroid(鸿蒙版)开发的第二篇 3、WanAndroid(鸿蒙版)开发的第三篇 …...
全国农产品价格分析预测可视化系统设计与实现
全国农产品价格分析预测可视化系统设计与实现 【摘要】在当今信息化社会,数据的可视化已成为决策和分析的重要工具。尤其是在农业领域,了解和预测农产品价格趋势对于农民、政府和相关企业都至关重要。为了满足这一需求,设计并实现了全国农产…...

堆排序(数据结构)
本期讲解堆排序的实现 —————————————————————— 1. 堆排序 堆排序即利用堆的思想来进行排序,总共分为两个步骤: 1. 建堆 • 升序:建大堆 • 降序:建小堆 2. 利用堆删除思想来进行排序. 建堆和堆删…...
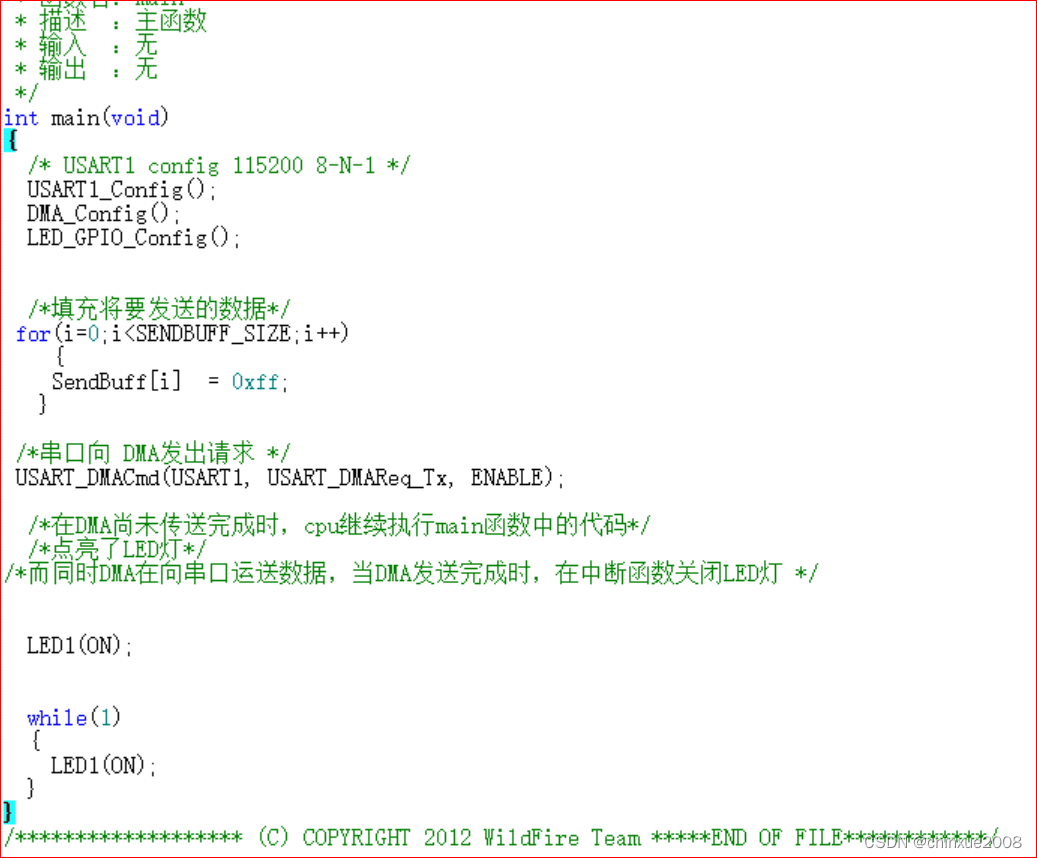
使用DMA方式控制串口
本身DMA没什么问题,但是最后用GPIOB点灯,就是点不亮。 回到原来GPIO点灯程序,使用GPIOB就是不亮,替换为GPIOA就可以,简单问题总是卡得很伤。...
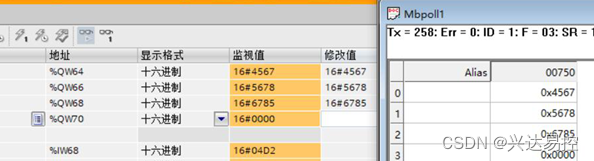
ModbusTCP转Profinet网关高低字节交换切换
背景:在现场设备与设备通迅之间通常涉及到从一种字节序(大端或小端)转换到另一种字节序。大端字节序是指高位字节存储在高地址处,而小端字节序是指低位字节存储在低地址处。在不动原有程序而又不想或不能添加程序下可选用ModbusTC…...
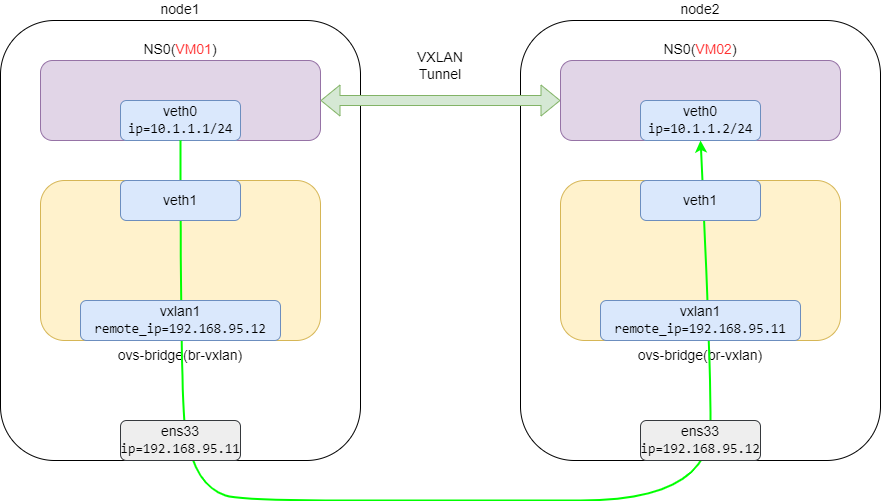
OpenvSwitch VXLAN 隧道实验
OpenvSwitch VXLAN 隧道实验 最近在了解 openstack 网络,下面基于ubuntu虚拟机安装OpenvSwitch,测试vxlan的基本配置。 节点信息: 主机名IP地址OS网卡node1192.168.95.11Ubuntu 22.04ens33node2192.168.95.12Ubuntu 22.04ens33 网卡信息&…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...
)
MySQL基本操作(续)
第3章:MySQL基本操作(续) 3.3 表操作 表是关系型数据库中存储数据的基本结构,由行和列组成。在MySQL中,表操作包括创建表、查看表结构、修改表和删除表等。本节将详细介绍这些操作。 3.3.1 创建表 在MySQL中&#…...

C++ 变量和基本类型
1、变量的声明和定义 1.1、变量声明规定了变量的类型和名字。定义初次之外,还申请存储空间,也可能会为变量赋一个初始值。 如果想声明一个变量而非定义它,就在变量名前添加关键字extern,而且不要显式地初始化变量: e…...
