【算法经典题集】前缀和与数学(持续更新~~~)
😽PREFACE
🎁欢迎各位→点赞👍 + 收藏⭐ + 评论📝
📢系列专栏:算法经典题集
🔊本专栏涉及到的知识点或者题目是算法专栏的补充与应用
💪种一棵树最好是十年前其次是现在
前缀和
一维前缀和
k倍区间
给定一个长度为 N 的数列,A1,A2,…AN,如果其中一段连续的子序列 Ai,Ai+1,…Aj之和是 K 的倍数,我们就称这个区间 [i,j] 是 K 倍区间。
你能求出数列中总共有多少个 K 倍区间吗?
输入格式
第一行包含两个整数 N 和 K。
以下 N 行每行包含一个整数 Ai。
输出格式
输出一个整数,代表 K 倍区间的数目。
数据范围
1≤N,K≤100000
1≤Ai≤100000
输入样例:
5 2
1
2
3
4
5
输出样例:
6
分析:求区间[l,r]的和是k的倍数的个数。求区间和,我们可以通过前缀和来求出。我们规定sum[i]表示第1个元素到第i个元素的和。那么sum[r] - sum[l-1]就是区间[l,r]的和。区间[l,r]的和是k的倍数即(sum[r] - sum[l-1])%k == 0 即sum[r]%k == sum[l-1]%k。对前缀和取模之后,两个相等的前缀和就能组成一个k倍区间。
总共出现了3次模为1的情况,而每两次模为1组合起来可以模0,比如1,2加起来模为1,1,2,3,4,5加起来模为1,那么这两种情况组合起来(区间做减)是3,4,5就是模为0的情况。所以一共出现了3次模为1的情况,那么两两组合的情况一共有三种,再加上本来模为0的情况有3次,一共就6次模为0的情况。“k倍区间就加上cnt[sum[i]]”只是实现了计算模不为0的时候的情况两两组合的组合数量。
按前缀和做差来想
①1=1②1+2=3③1+2+3=6④1+2+3+4=10⑤1+2+3+4+5=15
3次模为1的情况是①②⑤
两两组合后模为0,即:②-①=2;⑤-①=2+3+4+5=14;⑤-②=3+4+5=12
本来模为0的情况有③④,组合后得到4,即一共3种情况
3+3=6

#include <iostream>
#include <cstdio>
using namespace std;
int n, k;
int sum[100005], cnt[100005];
long long ans = 0;
int main()
{scanf("%d%d", &n, &k);for (int i = 1; i <= n; i++){int x;scanf("%d", &x);sum[i] += (sum[i - 1] + x) % k;// 求前缀和 ans += cnt[sum[i]];// 加上在此之前与它同余的前缀和(模k后) cnt[sum[i]]++;// 对前缀和模k后的余数统计出现次数 }printf("%lld", ans + cnt[0]);return 0;
}二维前缀和
激光炸弹
地图上有 N 个目标,用整数 Xi,Yi表示目标在地图上的位置,每个目标都有一个价值 Wi。
注意:不同目标可能在同一位置。
现在有一种新型的激光炸弹,可以摧毁一个包含 R×R个位置的正方形内的所有目标。
激光炸弹的投放是通过卫星定位的,但其有一个缺点,就是其爆炸范围,即那个正方形的边必须和 x,y轴平行。
求一颗炸弹最多能炸掉地图上总价值为多少的目标。
输入格式
第一行输入正整数 N 和 R,分别代表地图上的目标数目和正方形包含的横纵位置数量,数据用空格隔开。
接下来 N 行,每行输入一组数据,每组数据包括三个整数 Xi,Yi,Wi,分别代表目标的 x 坐标,y 坐标和价值,数据用空格隔开。
输出格式
输出一个正整数,代表一颗炸弹最多能炸掉地图上目标的总价值数目。
数据范围
0≤R≤10^9
0<N≤10000
0≤Xi,Yi≤5000
0≤Wi≤1000
输入样例:
2 1
0 0 1
1 1 1
输出样例:
1
#include <bits/stdc++.h>using namespace std;const int N = 5e3 + 10; int s[N][N];
int n, r;int main() {cin >> n >> r;r = min(5001, r); // 因为r最大可以取 10^9for (int i = 0; i < n; i++) {int x, y, w;cin >> x >> y >> w;s[++x][++y] += w; //右移一位, 就不需要考虑边界了, 并且必须是+=, 不能是=, 因为1个位置可能有多个目标}for (int i = 1; i <= 5001; i++) {for (int j = 1; j <= 5001; j++) {s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];}}int ans = 0;for (int i = r; i <= 5001; i++) {for (int j = r; j <= 5001; j++) {ans = max(ans, s[i][j] - s[i - r][j] - s[i][j - r] + s[i - r][j - r]);}}cout << ans << endl;return 0;
}数学
买不到的数目
小明开了一家糖果店。
他别出心裁:把水果糖包成4颗一包和7颗一包的两种。
糖果不能拆包卖。
小朋友来买糖的时候,他就用这两种包装来组合。
当然有些糖果数目是无法组合出来的,比如要买 10 颗糖。
你可以用计算机测试一下,在这种包装情况下,最大不能买到的数量是17。
大于17的任何数字都可以用4和7组合出来。
本题的要求就是在已知两个包装的数量时,求最大不能组合出的数字。
输入格式
两个正整数 n,m,表示每种包装中糖的颗数。
输出格式
一个正整数,表示最大不能买到的糖数。
数据范围
2≤n,m≤1000,
保证数据一定有解。
输入样例:
4 7
输出样例:
17
#include <bits/stdc++.h>
using namespace std;
int main()
{int p,q;cin>>p>>q;cout<<(p-1)*(q-1)-1<<endl;return 0;
}蚂蚁感冒
长 100 厘米的细长直杆子上有 n 只蚂蚁。
它们的头有的朝左,有的朝右。
每只蚂蚁都只能沿着杆子向前爬,速度是 1 厘米/秒。
当两只蚂蚁碰面时,它们会同时掉头往相反的方向爬行。
这些蚂蚁中,有 1 只蚂蚁感冒了。
并且在和其它蚂蚁碰面时,会把感冒传染给碰到的蚂蚁。
请你计算,当所有蚂蚁都爬离杆子时,有多少只蚂蚁患上了感冒。
输入格式
第一行输入一个整数 n, 表示蚂蚁的总数。
接着的一行是 n 个用空格分开的整数 Xi, Xi 的绝对值表示蚂蚁离开杆子左边端点的距离。
正值表示头朝右,负值表示头朝左,数据中不会出现 0 值,也不会出现两只蚂蚁占用同一位置。
其中,第一个数据代表的蚂蚁感冒了。
输出格式
输出1个整数,表示最后感冒蚂蚁的数目。
数据范围
1<n<50,
0<|Xi|<100
输入样例1:
3
5 -2 8
输出样例1:
1
输入样例2:
5
-10 8 -20 12 25
输出样例2:
3
#include <bits/stdc++.h>using namespace std;const int N = 55;int n;
int x[N];int main()
{cin >> n;for (int i = 0; i < n; i ++ ) cin >> x[i];int left = 0, right = 0; // 分别表示左边向右走的蚂蚁数量,和右边向左走的蚂蚁数量for (int i = 1; i < n; i ++ )if (abs(x[i]) < abs(x[0]) && x[i] > 0) left ++ ;else if (abs(x[i]) > abs(x[0]) && x[i] < 0) right ++ ;if (x[0] > 0 && right == 0 || x[0] < 0 && left == 0) cout << 1 << endl;else cout << left + right + 1 << endl;return 0;
}饮料换购
乐羊羊饮料厂正在举办一次促销优惠活动。乐羊羊C型饮料,凭3个瓶盖可以再换一瓶C型饮料,并且可以一直循环下去(但不允许暂借或赊账)。
请你计算一下,如果小明不浪费瓶盖,尽量地参加活动,那么,对于他初始买入的 n 瓶饮料,最后他一共能喝到多少瓶饮料。
输入格式
输入一个整数 n,表示初始买入的饮料数量。
输出格式
输出一个整数,表示一共能够喝到的饮料数量。
数据范围
0<n<10000
输入样例:
100
输出样例:
149
#include <iostream>using namespace std;int main()
{int n;cin >> n;int res = n;while (n >= 3){res += n / 3;n = n / 3 + n % 3;}cout << res << endl;return 0;
}相关文章:

【算法经典题集】前缀和与数学(持续更新~~~)
😽PREFACE🎁欢迎各位→点赞👍 收藏⭐ 评论📝📢系列专栏:算法经典题集🔊本专栏涉及到的知识点或者题目是算法专栏的补充与应用💪种一棵树最好是十年前其次是现在前缀和一维前缀和k倍…...

寻找时空中的引力波:科学家控制量子运动至量子基态
据英国每日邮报报道,时空织布里的涟漪或可以揭示宇宙在140亿年前是如何产生的,然而寻找这些名为“引力波”的涟漪却一直难以捉摸。现在美国科学家们声称他们发现了改善用于检测宇宙大爆炸的引力波的探测器的方法。 宇宙大爆炸残留的引力波 美国加州理…...
第六讲:ambari-web 模块二次开发
上述图片为 Ambari 部署及操作 hdp 集群相关的部分界面截图。这些页面如果想调整的话,比如汉化,二次开发等,则可以修改 ambari-web 模块的源码来实现。 一、介绍 ambari-web 模块涉及到的界面有: HDP 集群部署向导已安装服务的仪表板、配置界面等主机列表及详细信息告警列…...

echarts--提示框显示不全问题记录
最近接手一个同事之前做的网页,发现里面使用echarts来绘制各类图表;有2个问题一个是提示框显示不全,另一个就是绘制总是有部分数据显示不全。后者就是div宽度问题。。。无语,说下前面一个问题吧,记录一下。 tooltip组…...

LeetCode 1653. 使字符串平衡的最少删除次数
LeetCode 1653. 使字符串平衡的最少删除次数 难度:middle\color{orange}{middle}middle Rating:1794\color{orange}{1794}1794 题目描述 给你一个字符串 sss ,它仅包含字符 ′a′a′a′ 和 ′b′b′b′ 。 你可以删除 sss 中任意…...

聊一聊代码重构——程序方法和类上的代码实践
使用工厂方法取代构造方法 构造方法的问题 我们使用构造方法来初始化对象时候,我们得到的只能是当前对象。而使用工厂方法替换构造方法,我们可以返回其子类型或者代理类型。这让我们可以通过不同的实现类来进行逻辑实现的变化。 更重要的一点是&#…...
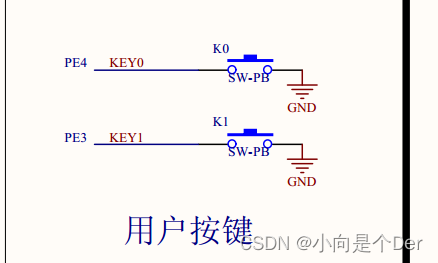
嵌入式学习笔记——寄存器开发STM32 GPIO口
寄存器开发STM32GPIO口前言认识GPIOGPIO是什么GPIO有什么用GPIO怎么用STM32上GPIO的命名以及数量GPIO口的框图(重点)输入框图解析三种输入模式GPIO输入时内部器件及其作用1.保护二极管2.上下拉电阻(可配置)3.施密特触发器4.输入数…...
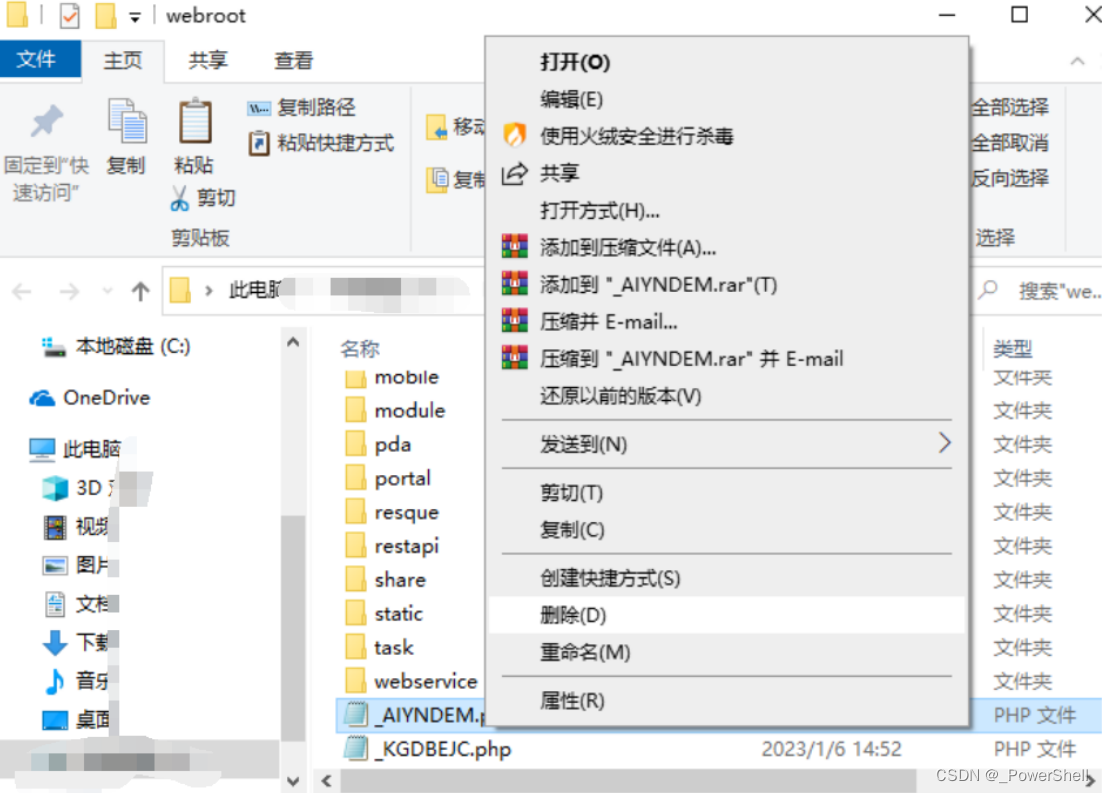
[ 攻防演练演示篇 ] 利用通达OA 文件上传漏洞上传webshell获取主机权限
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...

程序设计与 C 语言期末复习
程序设计与 C 语言 1.计算机语言与编译 机器语言:一串仅由 0 和 1 序列表示的语言。计算机只能识别和接受 0 和 1 组成的指令。 符号语言(汇编语言):用一些英文字母和数字表示一个指令。 符号语言(汇编语言…...
05-思维导图Xmind快速入门
文章目录5.1 认识思维导图5.2 Xmind的主要结构及主题元素5.2.1 Xmind的多种结构5.2.2 主题分类5.2.3 Xmind的主题元素章节总结5.1 认识思维导图 什么是思维导图? 思维导图是一种将思维进行可视化的实用工具。 具体实现方法是用一个关键词去引发相关想法࿰…...
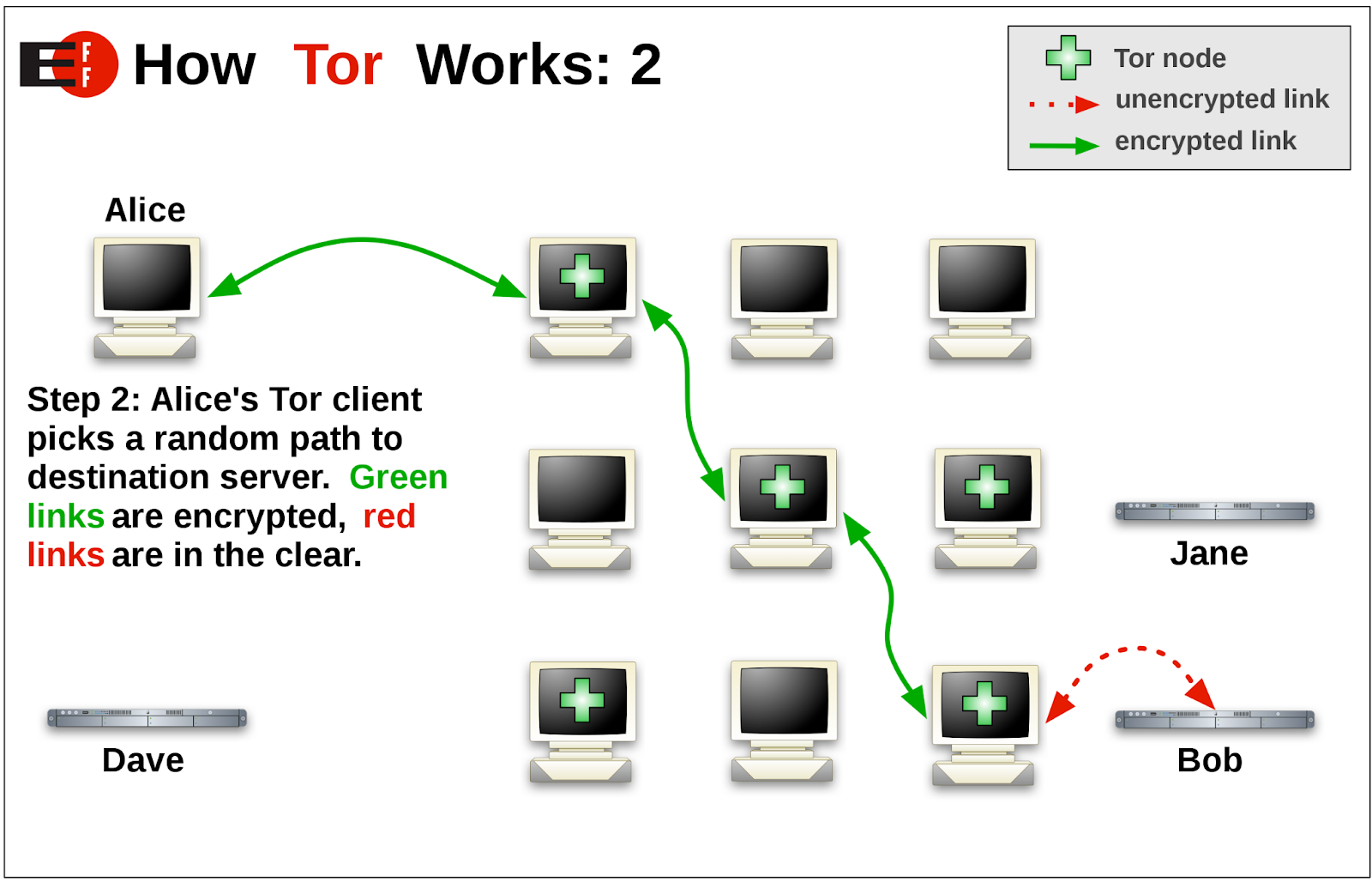
使用去中心化存储构建网站
今天的大多数网站都遵循后端服务器到前端代码的架构。但在 Web3 应用程序中,前端代码不具有与受智能合约保护的后端代码相同的去中心化性和弹性。那么如何使网站像智能合约一样具有弹性呢? 该体系结构似乎很简单: 创建一个没有服务器的静态…...

L - Let‘s Swap(哈希 + 规律)
2023河南省赛组队训练赛(四) - Virtual Judge (vjudge.net) 约瑟夫最近开发了一款名为Pandote的编辑软件,现在他正在测试,以确保它能正常工作,否则,他可能会被解雇!Joseph通过实现对Pandote上字符串的复制和…...
)
c语言自动内存回收(RAII实现)
简述 什么是RAII RAII(Resource Acquisition Is Initialization)是c之父Bjarne Stroustrup提出的概念。资源一般分三个步骤:获取、使用和销毁,而在自由使用内存的c语言中,资源的销毁常常是程序员容易遗漏的事情&…...
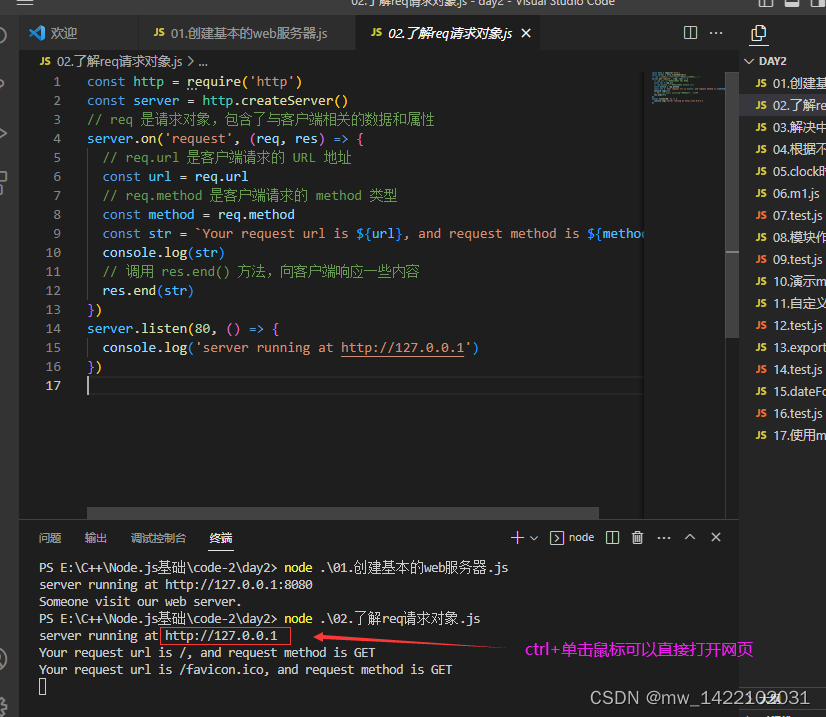
Node.js的简单学习一-----未完待续
文章目录前言学习目标一、初识Node.js1.1 回顾与思考1.1.1 需要掌握那些技术1.1.2 浏览器中的JavaScript的组成部分1.2 Node.js简介1 什么是Node.js2 Node.js中的JavaScript运行环境3 Node.js 可以做什么1.3 Node.js环境的安装1.4 在Node.js环境中执行JavaScript 代码终端中的快…...
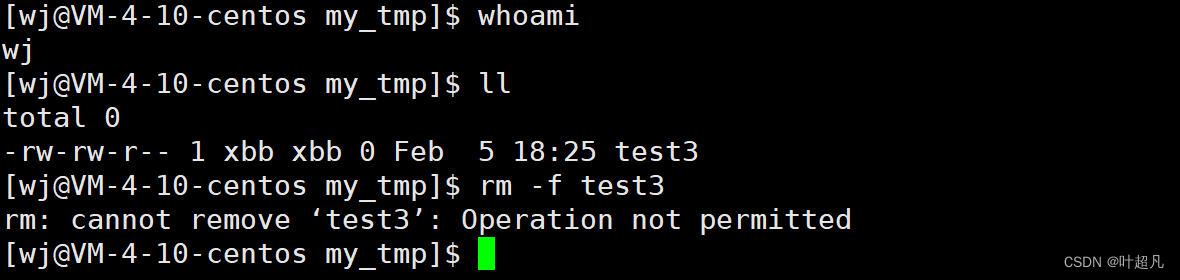
linux入门---粘滞位
为什么会有粘滞位 一台服务器有很多人使用,每个人在机器上都会有一个家目录,在家目录里可以实现自己想要的操作,但是有时候我们需要一个公共路径来完成一些操作,比如说资料分享产生临时文件的增删查改等等,这就好比我…...

关于正则表达式的讲解
以下内容源于《linux命令行与shell脚本编程大全【第三版】》一书的整理。 在shell脚本中成功运用sed编辑器和gawk程序的关键,在于熟练地使用正则表达式。 一、正则表达式的简介 1、正则表达式的定义 正则表达式(regular expression)是一个…...

贝塞尔曲线与B样条曲线
文章目录0.参考1.问题起源与插值法的曲线拟合1.1.问题起源1.2.拉格朗日插值1.3.“基”的概念1.4.插值存在的Runge现象2.贝塞尔曲线2.1.控制点的思想2.2.由控制点生成贝塞尔曲线2.3.多个控制点时的贝塞尔曲线公式2.4.贝塞尔曲线的递推公式2.5.贝塞尔曲线的性质3.B样条曲线3.1.B样…...

C语言-基础了解-24-C头文件
C头文件 一、C 头文件 头文件是扩展名为 .h 的文件,包含了 C 函数声明和宏定义,被多个源文件中引用共享。有两种类型的头文件:程序员编写的头文件和编译器自带的头文件。 在程序中要使用头文件,需要使用 C 预处理指令 #include…...
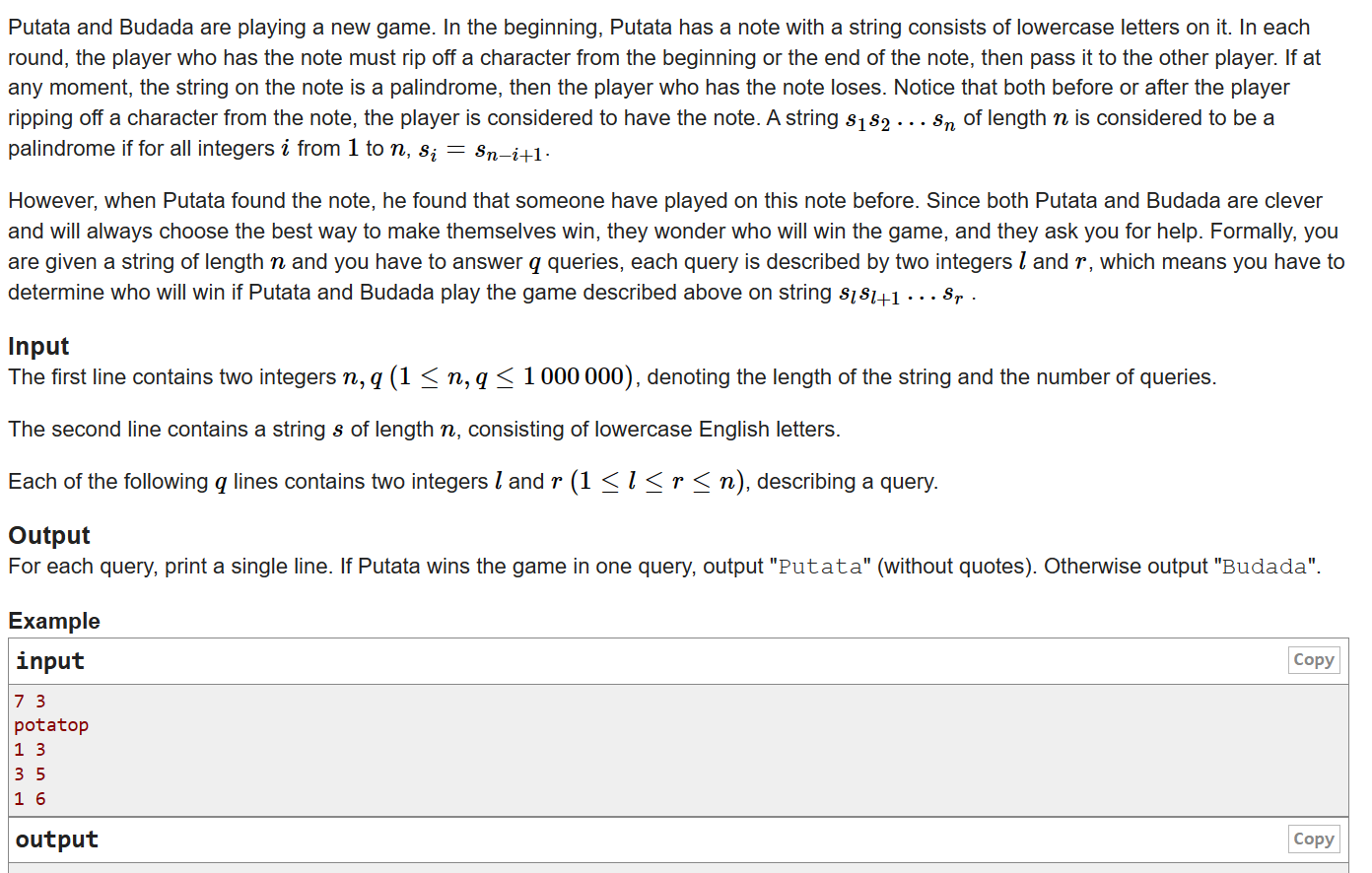
The 19th Zhejiang Provincial Collegiate Programming Contest vp
和队友冲了这场,极限6题,重罚时铁首怎么说,前面的A题我贡献了太多的罚时,然后我的G题最短路调了一万年,因为太久没写了,甚至把队列打成了优先队列,没把head数组清空完全,都是我的锅呜…...

用于<分类>的卷积神经网络、样本不平衡问题的解决
输入图像——卷积层——池化层——全连接层——输出 卷积层:核心,用来提取特征。 池化层:对特征降维。实际的主要作用是下采样,减少参数量来提高计算速度。 卷积神经网络的训练:前向传播(分类识别…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
