C语言经典算法-8
文章目录
- 其他经典例题跳转链接
- 41.基数排序法
- 42.循序搜寻法(使用卫兵)
- 43.二分搜寻法(搜寻原则的代表)
- 44.插补搜寻法
- 45.费氏搜寻法
其他经典例题跳转链接
C语言经典算法-1
1.汉若塔 2. 费式数列 3. 巴斯卡三角形 4. 三色棋 5. 老鼠走迷官(一)6. 老鼠走迷官(二)7. 骑士走棋盘8. 八皇后9. 八枚银币10. 生命游戏
C语言经典算法-2
字串核对、双色、三色河内塔、背包问题(Knapsack Problem)、蒙地卡罗法求 PI、Eratosthenes筛选求质数
C语言经典算法-3
超长整数运算(大数运算)、长 PI、最大公因数、最小公倍数、因式分解、完美数、阿姆斯壮数
C语言经典算法-4
最大访客数、中序式转后序式(前序式)、后序式的运算、洗扑克牌(乱数排列)、Craps赌博游戏
C语言经典算法-5
约瑟夫问题(Josephus Problem)、排列组合、格雷码(Gray Code)、产生可能的集合、m元素集合的n个元素子集
C语言经典算法-6
数字拆解、得分排行,选择、插入、气泡排序、Shell 排序法 - 改良的插入排序、Shaker 排序法 - 改良的气泡排序
C语言经典算法-7
排序法 - 改良的选择排序、快速排序法(一)、快速排序法(二)、快速排序法(三)、合并排序法
C语言经典算法-8
基数排序法、循序搜寻法(使用卫兵)、二分搜寻法(搜寻原则的代表)、插补搜寻法、费氏搜寻法
C语言经典算法-9
稀疏矩阵、多维矩阵转一维矩阵、上三角、下三角、对称矩阵、奇数魔方阵、4N 魔方阵、2(2N+1) 魔方阵
41.基数排序法
说明在之前所介绍过的排序方法,都是属于「比较性」的排序法,也就是每次排序时 ,都是比较整个键值的大小以进行排序。
这边所要介绍的「基数排序法」(radix sort)则是属于「分配式排序」(distribution sort),基数排序法又称「桶子法」(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些「桶」中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog®m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的比较性排序法。
解法基数排序的方式可以采用LSD(Least sgnificant digital)或MSD(Most sgnificant digital),LSD的排序方式由键值的最右边开始,而MSD则相反,由键值的最左边开始。
以LSD为例,假设原来有一串数值如下所示:
73, 22, 93, 43, 55, 14, 28, 65, 39, 81
首先根据个位数的数值,在走访数值时将它们分配至编号0到9的桶子中:

接下来将这些桶子中的数值重新串接起来,成为以下的数列:
81, 22, 73, 93, 43, 14, 55, 65, 28, 39
接着再进行一次分配,这次是根据十位数来分配:

接下来将这些桶子中的数值重新串接起来,成为以下的数列:
14, 22, 28, 39, 43, 55, 65, 73, 81, 93
这时候整个数列已经排序完毕;如果排序的对象有三位数以上,则持续进行以上的动作直至最高位数为止。
LSD的基数排序适用于位数小的数列,如果位数多的话,使用MSD的效率会比较好,MSD的方式恰与LSD相反,是由高位数为基底开始进行分配,其他的演 算方式则都相同。
#include <stdio.h>
#include <stdlib.h> int main(void) { int data[10] = {73, 22, 93, 43, 55, 14, 28, 65, 39, 81}; int temp[10][10] = {0}; int order[10] = {0}; int i, j, k, n, lsd; k = 0; n = 1; printf("\n排序前: "); for(i = 0; i < 10; i++) printf("%d ", data[i]); putchar('\n'); while(n <= 10) { for(i = 0; i < 10; i++) { lsd = ((data[i] / n) % 10); temp[lsd][order[lsd]] = data[i]; order[lsd]++; } printf("\n重新排列: "); for(i = 0; i < 10; i++) { if(order[i] != 0) for(j = 0; j < order[i]; j++) { data[k] = temp[i][j]; printf("%d ", data[k]); k++; } order[i] = 0; } n *= 10; k = 0; } putchar('\n'); printf("\n排序后: "); for(i = 0; i < 10; i++) printf("%d ", data[i]); return 0;
}
42.循序搜寻法(使用卫兵)
说明
搜寻的目的,是在「已排序的资料」中寻找指定的资料,而当中循序搜寻是最基本的搜寻法,只要从资料开头寻找到最后,看看是否找到资料即可。
解法
初学者看到循序搜寻,多数都会使用以下的方式来进行搜寻:
while(i < MAX) { if(number[i] == k) { printf("找到指定值"); break; } i++;
}
这个方法基本上没有错,但是可以加以改善,可以利用设定卫兵的方式,省去if判断式,卫兵通常设定在数列最后或是最前方,假设设定在列前方好了(索引0的 位置),我们从数列后方向前找,如果找到指定的资料时,其索引值不是0,表示在数列走访完之前就找到了,在程式的撰写上,只要使用一个while回圈就可 以了。
下面的程式为了配合卫兵的设置,自行使用快速排序法先将产生的数列排序,然后才进行搜寻,若只是数字的话,通常您可以使用程式语言函式库所提供的搜寻函式。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {int t; t = x; x = y; y = t;} int search(int[]);
int partition(int[], int, int);
void quicksort(int[], int, int); int main(void) { int number[MAX+1] = {0}; int i, find; srand(time(NULL)); for(i = 1; i <= MAX; i++) number[i] = rand() % 100; quicksort(number, 1, MAX); printf("数列:"); for(i = 1; i <= MAX; i++) printf("%d ", number[i]); printf("\n输入搜寻值:"); scanf("%d", &number[0]); if(find = search(number)) printf("\n找到数值于索引 %d ", find); else printf("\n找不到数值"); printf("\n"); return 0;
} int search(int number[]) { int i, k; k = number[0]; i = MAX; while(number[i] != k) i--; return i;
} int partition(int number[], int left, int right) { int i, j, s; s = number[right]; i = left - 1; for(j = left; j < right; j++) { if(number[j] <= s) { i++; SWAP(number[i], number[j]); } } SWAP(number[i+1], number[right]); return i+1;
} void quicksort(int number[], int left, int right) { int q; if(left < right) { q = partition(number, left, right); quicksort(number, left, q-1); quicksort(number, q+1, right); }
}
43.二分搜寻法(搜寻原则的代表)
说明如果搜寻的数列已经有排序,应该尽量利用它们已排序的特性,以减少搜寻比对的次数,这是搜寻的基本原则,二分搜寻法是这个基本原则的代表。
解法在二分搜寻法中,从数列的中间开始搜寻,如果这个数小于我们所搜寻的数,由于数列已排序,则该数左边的数一定都小于要搜寻的对象,所以无需浪费时间在左边的数;如果搜寻的数大于所搜寻的对象,则右边的数无需再搜寻,直接搜寻左边的数。
所以在二分搜寻法中,将数列不断的分为两个部份,每次从分割的部份中取中间数比对,例如要搜寻92于以下的数列,首先中间数索引为(0+9)/2 = 4(索引由0开始):
[3 24 57 57 67 68 83 90 92 95]
由于67小于92,所以转搜寻右边的数列:
3 24 57 57 67 [68 83 90 92 95]
由于90小于92,再搜寻右边的数列,这次就找到所要的数了:
3 24 57 57 67 68 83 90 [92 95]
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {int t; t = x; x = y; y = t;} void quicksort(int[], int, int);
int bisearch(int[], int); int main(void) { int number[MAX] = {0}; int i, find; srand(time(NULL)); for(i = 0; i < MAX; i++) { number[i] = rand() % 100; } quicksort(number, 0, MAX-1); printf("数列:"); for(i = 0; i < MAX; i++) printf("%d ", number[i]); printf("\n输入寻找对象:"); scanf("%d", &find); if((i = bisearch(number, find)) >= 0) printf("找到数字于索引 %d ", i); else printf("\n找不到指定数"); printf("\n"); return 0;
} int bisearch(int number[], int find) { int low, mid, upper; low = 0; upper = MAX - 1; while(low <= upper) { mid = (low+upper) / 2; if(number[mid] < find) low = mid+1; else if(number[mid] > find) upper = mid - 1; else return mid; } return -1;
} void quicksort(int number[], int left, int right) { int i, j, k, s; if(left < right) { s = number[(left+right)/2]; i = left - 1; j = right + 1; while(1) { while(number[++i] < s) ; // 向右找 while(number[--j] > s) ; // 向左找 if(i >= j) break; SWAP(number[i], number[j]); } quicksort(number, left, i-1); // 对左边进行递回 quicksort(number, j+1, right); // 对右边进行递回 }
}
44.插补搜寻法
说明
如果却搜寻的资料分布平均的话,可以使用插补(Interpolation)搜寻法来进行搜寻,在搜寻的对象大于500时,插补搜寻法会比 二分搜寻法 来的快速。
解法
插补搜寻法是以资料分布的近似直线来作比例运算,以求出中间的索引并进行资料比对,如果取出的值小于要寻找的值,则提高下界,如果取出的值大于要寻找的 值,则降低下界,如此不断的减少搜寻的范围,所以其本原则与二分搜寻法是相同的,至于中间值的寻找是透过比例运算,如下所示,其中K是指定要寻找的对象, 而m则是可能的索引值:
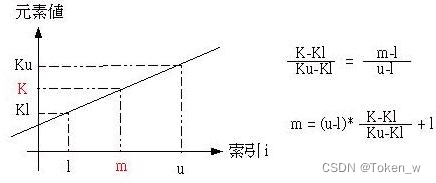
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {int t; t = x; x = y; y = t;} void quicksort(int[], int, int);
int intsrch(int[], int); int main(void) { int number[MAX] = {0}; int i, find; srand(time(NULL)); for(i = 0; i < MAX; i++) { number[i] = rand() % 100; } quicksort(number, 0, MAX-1); printf("数列:"); for(i = 0; i < MAX; i++) printf("%d ", number[i]); printf("\n输入寻找对象:"); scanf("%d", &find); if((i = intsrch(number, find)) >= 0) printf("找到数字于索引 %d ", i); else printf("\n找不到指定数"); printf("\n"); return 0;
} int intsrch(int number[], int find) { int low, mid, upper; low = 0; upper = MAX - 1; while(low <= upper) { mid = (upper-low)* (find-number[low])/(number[upper]-number[low]) + low; if(mid < low || mid > upper) return -1; if(find < number[mid]) upper = mid - 1; else if(find > number[mid]) low = mid + 1; else return mid; } return -1;
} void quicksort(int number[], int left, int right) { int i, j, k, s; if(left < right) { s = number[(left+right)/2]; i = left - 1; j = right + 1; while(1) { while(number[++i] < s) ; // 向右找 while(number[--j] > s) ; // 向左找 if(i >= j) break; SWAP(number[i], number[j]); } quicksort(number, left, i-1); // 对左边进行递回 quicksort(number, j+1, right); // 对右边进行递回 }
}
45.费氏搜寻法
说明
二分搜寻法每次搜寻时,都会将搜寻区间分为一半,所以其搜寻时间为O(log(2)n),log(2)表示以2为底的log值,这边要介绍的费氏搜寻,其利用费氏数列作为间隔来搜寻下一个数,所以区间收敛的速度更快,搜寻时间为O(logn)。
解法
费氏搜寻使用费氏数列来决定下一个数的搜寻位置,所以必须先制作费氏数列,这在之前有提过;费氏搜寻会先透过公式计算求出第一个要搜寻数的位置,以及其代 表的费氏数,以搜寻对象10个数字来说,第一个费氏数经计算后一定是F5,而第一个要搜寻的位置有两个可能,例如若在下面的数列搜寻的话(为了计算方便, 通常会将索引0订作无限小的数,而数列由索引1开始):
-infin; 1 3 5 7 9 13 15 17 19 20
如果要搜寻5的话,则由索引F5 = 5开始搜寻,接下来如果数列中的数小于指定搜寻值时,就往左找,大于时就向右,每次找的间隔是F4、F3、F2来寻找,当费氏数为0时还没找到,就表示寻找失败,如下所示:
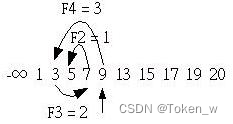
由于第一个搜寻值索引F5 = 5处的值小于19,所以此时必须对齐数列右方,也就是将第一个搜寻值的索引改为F5+2 = 7,然后如同上述的方式进行搜寻,如下所示:
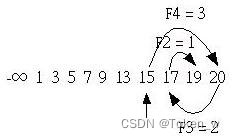
至于第一个搜寻值是如何找到的?我们可以由以下这个公式来求得,其中n为搜寻对象的个数:
Fx + m = n
Fx <= n
也就是说Fx必须找到不大于n的费氏数,以10个搜寻对象来说:
Fx + m = 10
取Fx = 8, m = 2,所以我们可以对照费氏数列得x = 6,然而第一个数的可能位置之一并不是F6,而是第x-1的费氏数,也就是F5 = 5。
如果数列number在索引5处的值小于指定的搜寻值,则第一个搜寻位置就是索引5的位置,如果大于指定的搜寻值,则第一个搜寻位置必须加上m,也就是F5 + m = 5 + 2 = 7,也就是索引7的位置,其实加上m的原因,是为了要让下一个搜寻值刚好是数列的最后一个位置。
费氏搜寻看来难懂,但只要掌握Fx + m = n这个公式,自己找几个实例算一次,很容易就可以理解;费氏搜寻除了收敛快速之外,由于其本身只会使用到加法与减法,在运算上也可以加快。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 15
#define SWAP(x,y) {int t; t = x; x = y; y = t;} void createfib(void); // 建立费氏数列
int findx(int, int); // 找x值
int fibsearch(int[], int); // 费氏搜寻
void quicksort(int[], int, int); // 快速排序 int Fib[MAX] = {-999}; int main(void) { int number[MAX] = {0}; int i, find; srand(time(NULL)); for(i = 1; i <= MAX; i++) { number[i] = rand() % 100; } quicksort(number, 1, MAX); printf("数列:"); for(i = 1; i <= MAX; i++) printf("%d ", number[i]); printf("\n输入寻找对象:"); scanf("%d", &find); if((i = fibsearch(number, find)) >= 0) printf("找到数字于索引 %d ", i); else printf("\n找不到指定数"); printf("\n"); return 0;
} // 建立费氏数列
void createfib(void) { int i; Fib[0] = 0; Fib[1] = 1; for(i = 2; i < MAX; i++) Fib[i] = Fib[i-1] + Fib[i-2];
} // 找 x 值
int findx(int n, int find) { int i = 0; while(Fib[i] <= n) i++; i--; return i;
} // 费式搜寻
int fibsearch(int number[], int find) { int i, x, m; createfib(); x = findx(MAX+1,find); m = MAX - Fib[x]; printf("\nx = %d, m = %d, Fib[x] = %d\n\n", x, m, Fib[x]); x--; i = x; if(number[i] < find) i += m; while(Fib[x] > 0) { if(number[i] < find) i += Fib[--x]; else if(number[i] > find) i -= Fib[--x]; else return i; } return -1;
} void quicksort(int number[], int left, int right) { int i, j, k, s; if(left < right) { s = number[(left+right)/2]; i = left - 1; j = right + 1; while(1) { while(number[++i] < s) ; // 向右找 while(number[--j] > s) ; // 向左找 if(i >= j) break; SWAP(number[i], number[j]); } quicksort(number, left, i-1); // 对左边进行递回 quicksort(number, j+1, right); // 对右边进行递回 }
}
系列好文,点击链接即可跳转
C语言经典算法-7
排序法 - 改良的选择排序、快速排序法(一)、快速排序法(二)、快速排序法(三)、合并排序法
C语言经典算法-9
稀疏矩阵、多维矩阵转一维矩阵、上三角、下三角、对称矩阵、奇数魔方阵、4N 魔方阵、2(2N+1) 魔方阵
相关文章:

C语言经典算法-8
文章目录 其他经典例题跳转链接41.基数排序法42.循序搜寻法(使用卫兵)43.二分搜寻法(搜寻原则的代表)44.插补搜寻法45.费氏搜寻法 其他经典例题跳转链接 C语言经典算法-1 1.汉若塔 2. 费式数列 3. 巴斯卡三角形 4. 三色棋 5. 老鼠…...

Panasonic松下PLC如何数据采集?如何实现快速接入IIOT云平台?
在工业自动化领域,数据采集与远程控制是提升生产效率、优化资源配置的关键环节。对于使用Panasonic松下PLC的用户来说,如何实现高效、稳定的数据采集,并快速接入IIOT云平台,是摆在他们面前的重要课题。HiWoo Box工业物联网关以其强…...

高性能 MySQL 第四版(GPT 重译)(四)
第十一章:扩展 MySQL 在个人项目中运行 MySQL,甚至在年轻公司中运行 MySQL,与在市��已经建立并且“呈现指数增长”业务中运行 MySQL 大不相同。在高速业务环境中,流量可能每年增长数倍,环境变得…...

整型数组按个位值排序 - 华为OD统一考试(C卷)
OD统一考试(C卷) 分值: 100分 题解: Java / Python / C 题目描述 给定一个非空数组(列表),其元素数据类型为整型,请按照数组元素十进制最低位从小到大进行排序,十进制最低位相同的元素…...

【React】Diff算法
1. React15 Diff算法(递归进行) 一句话概括:新虚拟DOM和旧虚拟DOM对比,找出差异,根据差异更新真实DOM Diff过程描述: 1. 树比较(DOM) 同层节点之间相互比较,不会跨层级比较。(当发现…...
【物联网】Modbus 协议及应用
Modbus 协议简介 QingHub设计器在设计物联网数据采集时不可避免的需要针对Modbus协议的设备做相关数据采集,这里就我们的实际项目经验分享Modbus协议 简介 Modbus由MODICON公司于1979年开发,是一种工业现场总线协议标准。1996年施耐德公司推出基于以太…...

Docker容器引擎
1、Docker是什么。 Docker是在Linux容器里运行应用的开源工具,是一种轻量级的"虚拟机"。Docker的logo设计为蓝色鲸鱼,拖着许多集装箱。鲸鱼可以看作宿主机,而集装箱可以理解为相互隔离的容器,每个集装箱中都包含自己的应…...

2.28线程
注意被抢占时是返回原队列,优先级不变。越往下优先级越小。往下没有优先级时,在最低的优先级队列里循环 到达了不一定会被服务,会进入就绪态进行等待 。核心等式就是周转时间运行时间等待时间,带权就是周转/运行, 随着…...
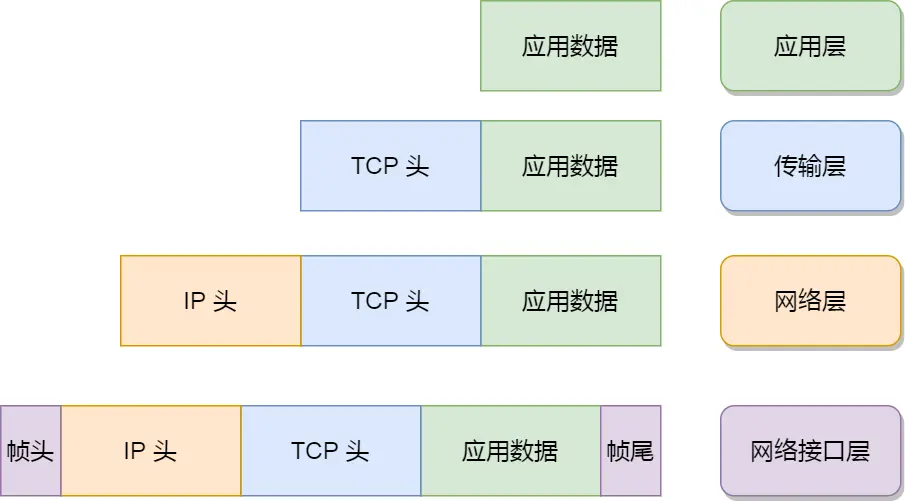
TCP/IP ⽹络模型
TCP/IP ⽹络模型 对于同⼀台设备上的进程间通信,有很多种⽅式,⽐如有管道、消息队列、共享内存、信号等⽅式,⽽对于不同设备上的进程间通信,就需要⽹络通信,⽽设备是多样性的,所以要兼容多种多样的设备&am…...

云原生:重塑未来应用的基石
随着数字化时代的不断深入,云原生已经成为了IT领域的热门话题。它代表着一种全新的软件开发和部署范式,旨在充分利用云计算的优势,并为企业带来更大的灵活性、可靠性和效率。今天我们就来聊一聊这个热门的话题:云原生~ Ǵ…...

蓝桥杯day4刷题日记
P8605 [蓝桥杯 2013 国 AC] 网络寻路 思路来源于https://www.luogu.com.cn/article/iat8irsf #include <iostream> using namespace std; int n,m; int q[10010]; int v[100010],u[100010]; long long res;int main() {cin>>n>>m;for(int i0;i<m;i){cin…...
[Qt学习笔记]Qt下使用Halcon实现采图时自动对焦的功能(Brenner梯度法)
目录 1、介绍2、实现方法2.1 算法实现过程2.2 模拟采集流程 3、总结4、代码展示 1、介绍 在机器视觉的开发中,现在有很多通过电机去做相机的聚焦调节,对比手工调节,自动调节效果更好,而且其也能满足设备自动的需求,尤…...

常州IGM机器人RTE497的日常维修保养方法
一、IGM机器人RTE497日常检查 每日工作前,进行以下检查: 外观检查:确认IGM机器人RTE497本体无明显损伤,各部件连接稳固。 电缆检查:检查所有电缆、气管等是否完好,无磨损、无挤压。 润滑检查:确…...

如何利用机器学习和Python编写预测模型来预测设备故障
预测设备故障是机器学习和数据科学的一个常见问题,通常可以通过以下几个步骤来解决: 1. 数据收集 首先,需要收集与设备运行相关的数据,包括: 设备的历史数据环境数据(如温度、湿度等)使用时间…...

mysql部署(2)主从复制
在前面的基础上,现有26、41两个mysql8的实例,下面以26为主41为从搭建主从复制: 机器主从端口号root密码主从复制账号密码xxx.xx.xxx.26主3306Mysql#26user1/user1#26xxx.xx.xxx.41从3306Mysql#41 一、master主库配置 1、修改mysql配置文件…...
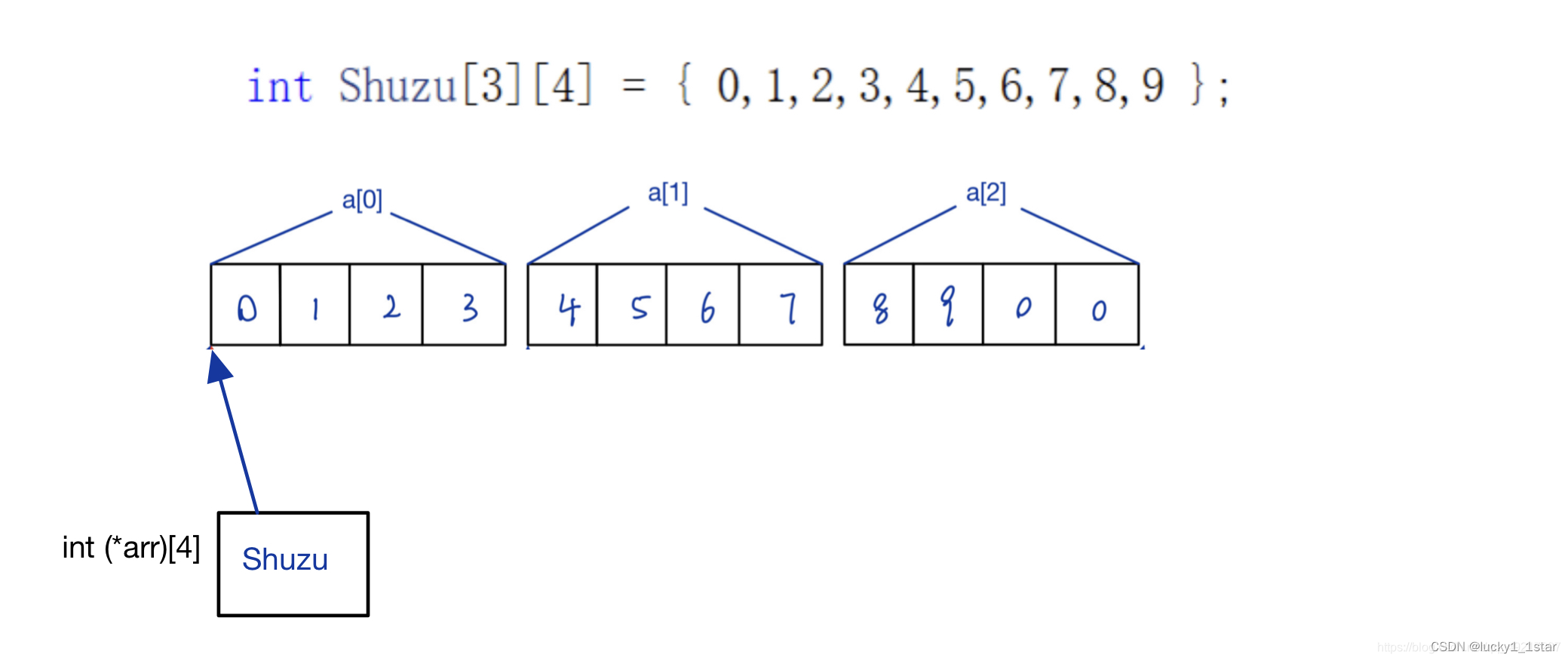
FX-数组的使用
1一维数组 1.1一维数组的创建和初始化 1.1.1数组的创建 //代码1 int arr1[10]; char arr2[10]; float arr3[1]; double arr4[20]; //代码2 //用宏定义的方式 #define X 3 int arr5[X]; //代码3 //错误使用 int count 10; int arr6[count];//数组时候可以正常创建࿱…...
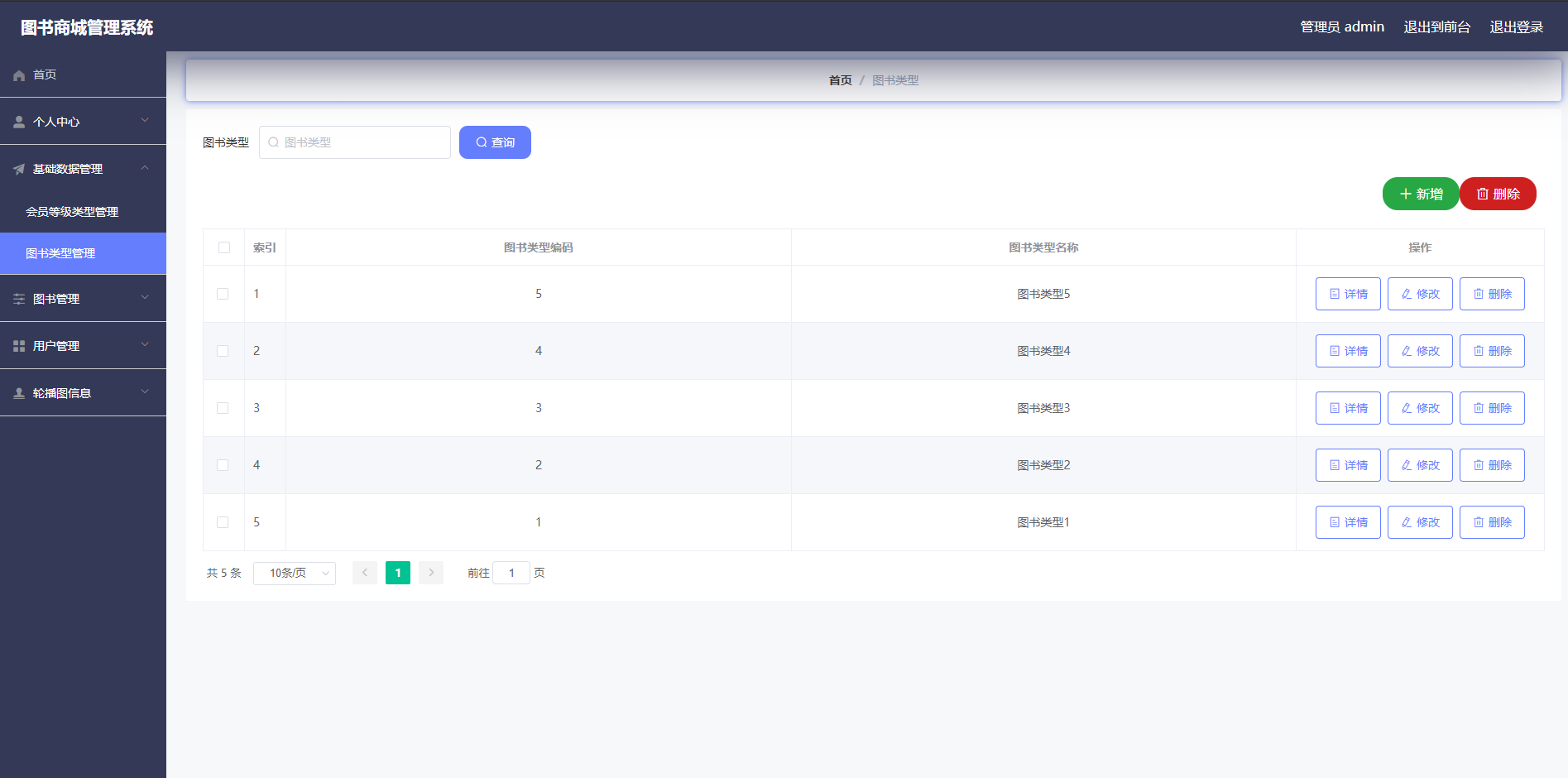
springboot283图书商城管理系统
图书商城管理系统 摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本图书商城管理系统就是在这样的大环境下诞生,其可以帮助管理者在短时间内处理…...

FFmpeg-- c++实现:音频流aac和视频流h264封装
文章目录 流程api核心代码muxer.hmuxer.cpp aac 和 h264 封装为视频流,封装为c的Muxter类 流程 分配视频文件上下文 int Init(const char *url); 创建流,赋值给视频的音频流和视频流 int AddStream(AVCodecContext *codec_ctx); 写视频流的head int Se…...

单片机烧录方式,JTAG,ISP,SWD,
常见的词汇 参考 ISP:In System Programing,在系统编程 IAP:In Application Programing,在应用编程 ICP:In Circuit Programing,在电路编程 ICSP全称是In Circuit Serial Programming JTAG(Joint Test Act…...
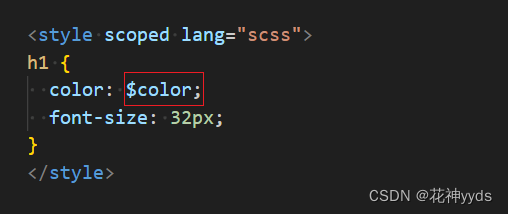
【项目管理后台】Vue3+Ts+Sass实战框架搭建一
项目管理后台 建立项目最好是卸载Vetur 新建.env.d.ts文件安装Eslint安装校验忽略文件添加运行脚本 安装prettier新建.prettierrc.json添加规则新建.prettierignore忽略文件 安装配置stylelint新建.stylelintrc.cjs 添加后的运行脚本配置husky配置commitlint配置husky 强制使用…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
