图论01-DFS和BFS(深搜和广搜邻接矩阵和邻接表/Java)
1.深度优先理论基础(dfs)
- dfs的两个关键操作
搜索方向,是认准一个方向搜,直到碰壁之后再换方向
换方向是撤销原路径,改为节点链接的下一个路径,回溯的过程。
- dfs解题模板
void dfs(参数) {if (终止条件) {存放结果;return;}for (选择:本节点所连接的其他节点) {处理节点;dfs(图,选择的节点); // 递归回溯,撤销处理结果}
}
- Java代码实现
邻接矩阵表示的图
public class DFSTraversalRecursive {private int[][] adjacencyMatrix; // 邻接矩阵private boolean[] visited; // 用于标记节点是否被访问过private int numNodes; // 节点数量public DFSTraversalRecursive(int[][] matrix) {this.adjacencyMatrix = matrix;this.numNodes = matrix.length;this.visited = new boolean[numNodes];}// 递归实现的深度优先搜索遍历public void dfsTraversalRecursive(int startNode) {visited[startNode] = true; // 标记当前节点为已访问System.out.print(startNode + " "); // 输出当前节点for (int i = 0; i < numNodes; i++) {// 如果存在从当前节点到节点 i 的边,并且节点 i 还未被访问过if (adjacencyMatrix[startNode][i] == 1 && !visited[i]) {dfsTraversalRecursive(i); // 递归调用,从节点 i 开始深度优先搜索}}}
}
邻接表表示的图
public class DFSTraversalAdjacencyList {private List<List<Integer>> adjacencyList; // 邻接表存储图的结构private boolean[] visited; // 标记节点是否被访问过// 构造函数,初始化邻接表和visited数组public DFSTraversalAdjacencyList(int numNodes) {this.adjacencyList = new ArrayList<>();for (int i = 0; i < numNodes; i++) {this.adjacencyList.add(new ArrayList<>());}this.visited = new boolean[numNodes];}// 添加边到邻接表public void addEdge(int source, int destination) {adjacencyList.get(source).add(destination);}// 递归实现的深度优先搜索遍历public void dfsTraversalRecursive(int startNode) {visited[startNode] = true; // 标记当前节点为已访问System.out.print(startNode + " "); // 输出当前节点// 遍历当前节点的所有邻居节点for (int neighbor : adjacencyList.get(startNode)) {if (!visited[neighbor]) {dfsTraversalRecursive(neighbor); // 递归调用,从邻居节点开始深度优先搜索}}}
2.广度优先搜索理论基础(bfs)
- 使用场景
广搜的搜索方式就适合于解决两个点之间的最短路径问题。因为广搜是从起点出发,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路
- Java代码实现
邻接矩阵表示的图
public class BFSTraversalAdjacencyMatrix {private int[][] adjacencyMatrix; // 邻接矩阵存储图的结构private boolean[] visited; // 标记节点是否被访问过public BFSTraversalAdjacencyMatrix(int numNodes) {this.adjacencyMatrix = new int[numNodes][numNodes]; // 初始化邻接矩阵this.visited = new boolean[numNodes]; // 初始化visited数组}// 添加边到邻接矩阵public void addEdge(int source, int destination) {adjacencyMatrix[source][destination] = 1;}// 广度优先搜索遍历public void bfsTraversal(int startNode) {Queue<Integer> queue = new LinkedList<>(); // 创建一个队列用于BFS遍历queue.add(startNode); // 将起始节点加入队列visited[startNode] = true; // 标记起始节点为已访问while (!queue.isEmpty()) {int currentNode = queue.poll(); // 出队列一个节点System.out.print(currentNode + " "); // 输出当前节点for (int i = 0; i < adjacencyMatrix.length; i++) {if (adjacencyMatrix[currentNode][i] == 1 && !visited[i]) {queue.add(i); // 将未访问的邻居节点加入队列visited[i] = true; // 标记邻居节点为已访问}}}}
}
邻接表表示的图
public class BFSTraversalAdjacencyList {private LinkedList<Integer>[] adjacencyList; // 邻接表存储图的结构private boolean[] visited; // 标记节点是否被访问过public BFSTraversalAdjacencyList(int numNodes) {// 初始化邻接表this.adjacencyList = new LinkedList[numNodes];for (int i = 0; i < numNodes; i++) {adjacencyList[i] = new LinkedList<Integer>();}// 初始化visited数组this.visited = new boolean[numNodes];}// 添加边到邻接表public void addEdge(int source, int destination) {adjacencyList[source].add(destination);}// 广度优先搜索遍历public void bfsTraversal(int startNode) {Queue<Integer> queue = new LinkedList<>(); // 创建一个队列用于BFS遍历queue.add(startNode); // 将起始节点加入队列visited[startNode] = true; // 标记起始节点为已访问while (!queue.isEmpty()) {int currentNode = queue.poll(); // 出队列一个节点System.out.print(currentNode + " "); // 输出当前节点for (int neighbor : adjacencyList[currentNode]) {if (!visited[neighbor]) {queue.add(neighbor); // 将未访问的邻居节点加入队列visited[neighbor] = true; // 标记邻居节点为已访问}}}}
}
相关文章:
)
图论01-DFS和BFS(深搜和广搜邻接矩阵和邻接表/Java)
1.深度优先理论基础(dfs) dfs的两个关键操作 搜索方向,是认准一个方向搜,直到碰壁之后再换方向 换方向是撤销原路径,改为节点链接的下一个路径,回溯的过程。dfs解题模板 void dfs(参数) {if (终止条件) {存放结果;return;}for …...
【Python】Miniconda+Vscode+Jupyter 环境搭建
1.安装 Miniconda Conda 是一个开源的包管理和环境管理系统,可在 Windows、macOS 和 Linux 上运行,它可以快速安装、运行和更新软件包及其依赖项。使用 Conda,我们可以轻松在本地计算机上创建、保存、加载和切换不同的环境 Conda 分为 Anaco…...
Redis消息队列与thinkphp/queue操作
业务场景 场景一 用户完成注册后需要发送欢迎注册的问候邮件、同时后台要发送实时消息给用户对应的业务员有新的客户注册、最后将用户的注册数据通过接口推送到一个营销用的第三方平台。 遇到两个问题: 由于代码是串行方式,流程大致为:开…...

【Ubuntu】常用命令
一般操作 pwd(present working directory) 显示当前的工作目录/路径。 cd (change directory) 改变目录,用于输入需要前往的路径/目录。 有一些特殊命令也很常用 : 解释 前往同一级的另一个目录 cd ../directory name cd .. 表示进入上…...
稀碎从零算法笔记Day22-LeetCode:
题型:链表 链接:2. 两数相加 - 力扣(LeetCode) 来源:Leet 题目描述 给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。 …...

Nacos下载和安装
(1)下载地址和版本 下载地址:Releases alibaba/nacos GitHub 解压在没有中文及空格的文件夹 (2)启动nacos服务 在bin目录下,打开命令行,输入 启动命令:sh startup.sh -m standalone - Linux/Unix/Mac …...
)
pandas简介(python)
pandas是什么 Pandas 是一个开源的第三方 Python 库,从 Numpy 和 Matplotlib 的基础上构建而来,享有数据分析“三剑客之一”的盛名(NumPy、Matplotlib、Pandas)。Pandas 已经成为 Python 数据分析的必备高级工具,它的…...

个人网站制作 Part 13 添加搜索功能[Elasticsearch] | Web开发项目
文章目录 👩💻 基础Web开发练手项目系列:个人网站制作🚀 添加搜索功能🔨使用Elasticsearch🔧步骤 1: 安装Elasticsearch🔧步骤 2: 配置Elasticsearch🔧步骤 3: 创建索引 …...

Springboot+vue的仓库管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。
演示视频: Springbootvue的仓库管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。 项目介绍: 采用M(model)V(view)C(controller)三层…...
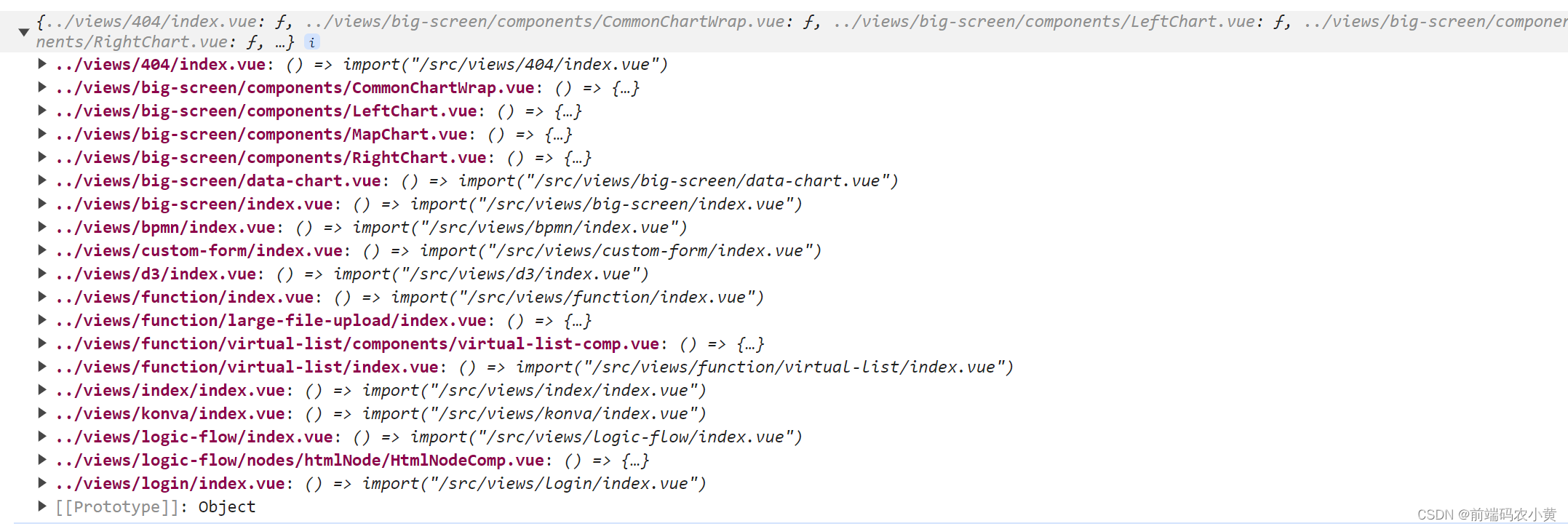
vue3 + vite 实现一个动态路由加载功能
假设后端返回的格式是这样子 {"menu": [{"path": "/admin","name": "adminLayout","redirect": "/admin/index","componentPath": "/layout/admin/index.vue","children&quo…...

【征稿进行时|见刊、检索快速稳定】2024年区块链、物联网与复合材料与国际学术会议 (ICBITC 2024)
【征稿进行时|见刊、检索快速稳定】2024年区块链、物联网与复合材料与国际学术会议 (ICBITC 2024) 大会主题: (主题包括但不限于, 更多主题请咨询会务组苏老师) 区块链: 区块链技术和系统 分布式一致性算法和协议 块链性能 信息储存系统 区块链可扩展性 区块…...

若依jar包运行脚本,从零到一:用Bash脚本实现JAR应用的启动、停止与监控
脚本使用说明: 启动应用:sh app.sh start停止应用:sh app.sh stop检查应用状态:sh app.sh status重启应用:sh app.sh restart 注意事项: 请确保你的系统上安装了 Java 环境,并且 ruoyi-admin…...
)
Unix运维_FreeBSD-13.1临时环境变量设置(bin和include以及lib)
Unix运维_FreeBSD-13.1临时环境变量设置(bin和include以及lib) 在 FreeBSD 系统上设置用户环境变量可以通过编辑用户的 Shell配置文件 来实现。 cshrc 与 csh_profile 的区别: cshrc: 每个脚本执行前都执行一遍这个脚本。 csh_profile: 根据不同使用者用户名, 会先去其 home…...
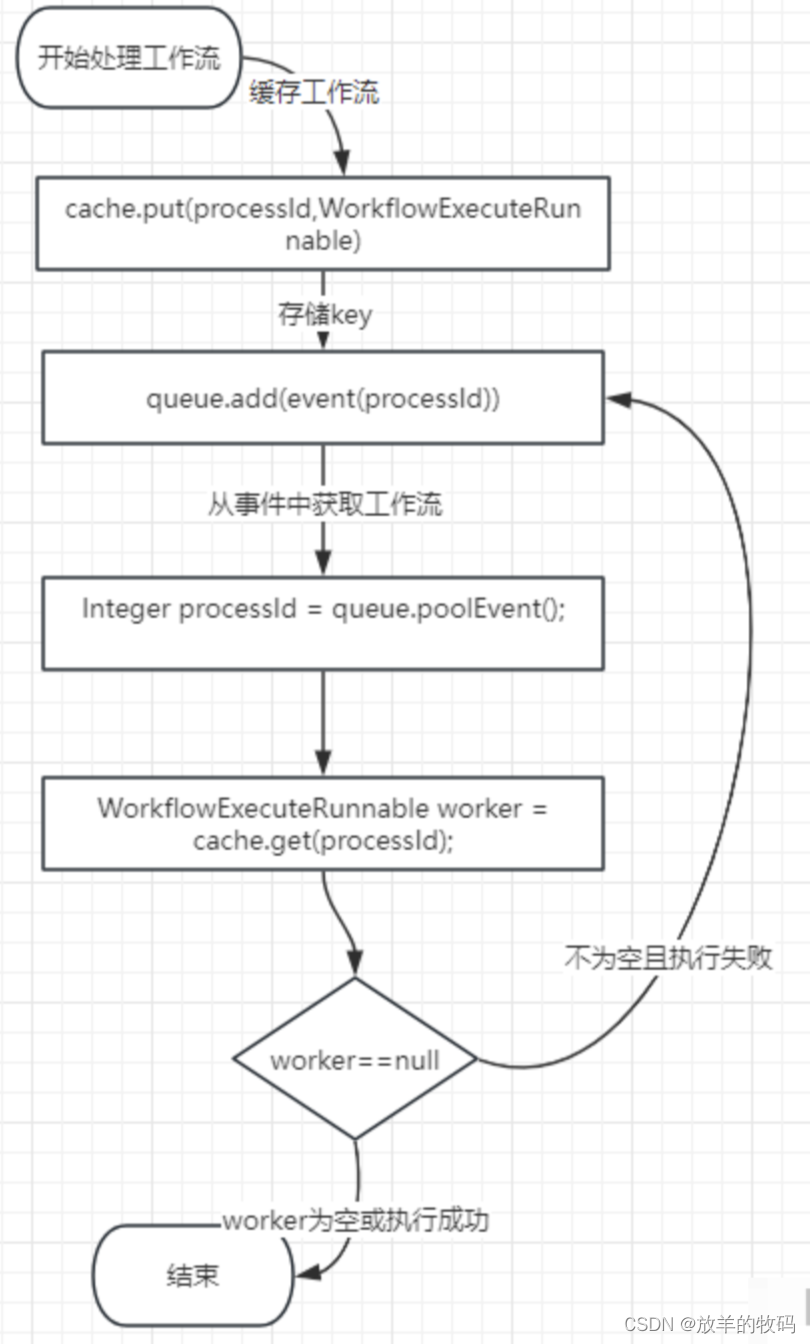
Apache Dolphinscheduler - 无需重启 Master-Server 停止疯狂刷日志解决方案
记录的是一个 3.0 比较难搞的问题,相信不少使用过 3.0 的用户都遇到过 Master 服务中存在一些工作流或者任务流一直不停的死循环的问题,导致疯狂刷日志。不过本人到现在也没找到最关键的触发原因,只是看到一些连锁反应带来的结果…… 影响因素…...

竞争优势:大型语言模型 (LLM) 如何重新定义业务策略
人工智能在内容创作中的突破 在当今快节奏的商业环境中,像 GPT-4 这样的大型语言模型 (LLM) 不再只是一种技术新颖性; 它们已成为重新定义跨行业业务战略的基石。 从增强客户服务到推动创新,法学硕士提供了企业不容忽视的竞争优势。 1. 加强…...

Spring AOP和AspectJ AOP区别
Spring AOP(Aspect-Oriented Programming)和 AspectJ AOP 是两种不同的 AOP 实现方式,它们在实现上有一些区别。下面是它们之间的主要区别: 基于代理 vs 字节码增强: Spring AOP: Spring AOP 是基于代理的…...
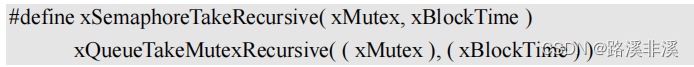
FREERTOS信号量详解
信号量是操作系统中重要的一部分,信号量一般用来进行资源管理和任务同步,资源管理其实就是用变量来标记现有资源的数量,任务同步其实就是用标志位来控制任务的先后执行顺序,这些概念在操作系统中以及裸机开发中都有所涉及。 FreeR…...

每天学习一个Linux命令之vim
每天学习一个Linux命令之vim Vim是一款功能强大的文本编辑器,在Linux系统中广泛使用。本篇博客将介绍一些常用的Vim命令及其选项,帮助您更好地使用Vim进行文本编辑。 命令及选项 以下是Vim的常用命令及其可用选项: 1. 打开文件 $ vim fi…...

linux环境部署
war包环境 在Linux系统上部署准备war包环境 查看linux当前版本和系统类型 [rootlocalhost ~]# uname -a Linux localhost.localdomain 3.10.0-1160.el7.x86_64 #1 SMP Mon Oct 19 16:18:59 UTC 2020 x86_64 x86_64 x86_64 GNU/Linuxlinux 打包文件夹 使用tar命令࿱…...
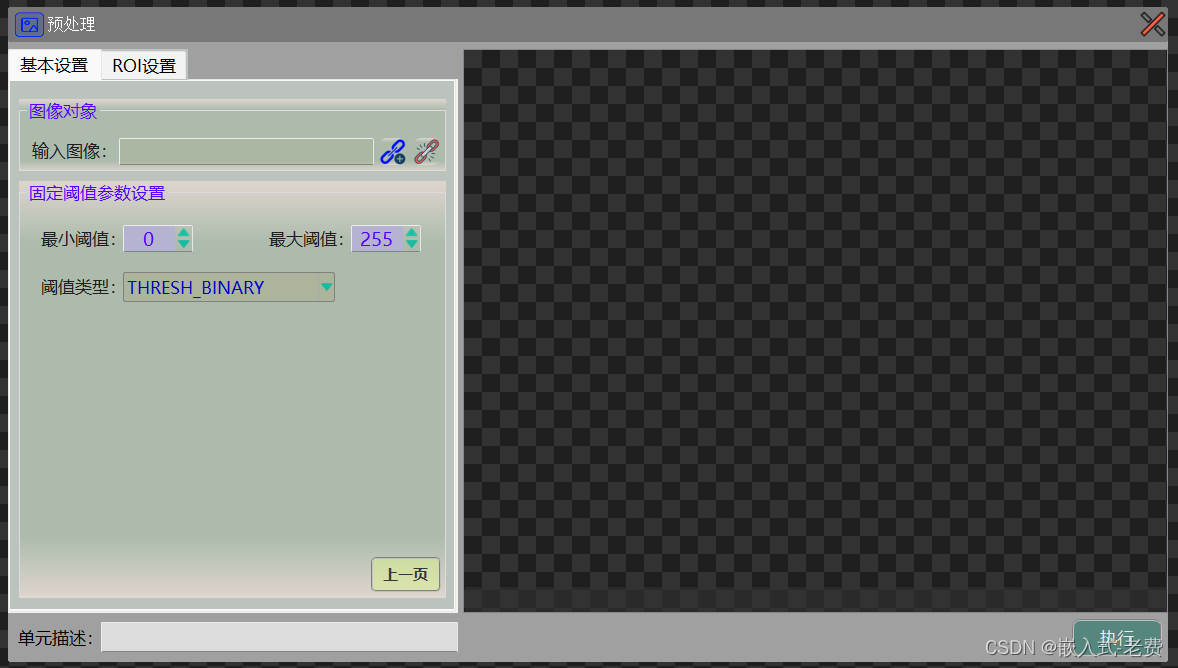
上位机图像处理和嵌入式模块部署(qmacvisual图像预处理)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 不管大家是在读书的时候学习的图像处理,还是在后来的工作中,重新学习了图像处理,相信大家对图像预处理的概念并…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
