多种智能搜索算法可视化还原 3D 魔方
2024/03/19:程序更新说明(文末程序下载链接已更新)
版本:v1.0 → v1.2
① 修复:将 CLOSED 表内容从优先级队列中分离开来,原优先级队列作 OPEN 表,并用链表树隐式地代替 CLOSED 表,以此修复之前版本内存爆炸的问题(尤其以 HC 爬山法严重);
② 优化:实时搜索树动态绘制,而非总是保持 10 行;
③ 其它:优化代码,修复其它的一些小问题;
一、写在前面
许久没有写图形化界面的程序了,最近学习了一些经典的盲目搜索算法与智能搜索算法,正好拿来还原三阶魔方!试试手!
提前声明
我不是专业搞人工智能的,理论或者实现过程有些许错误也很正常,评论区指出即可
先说一下开发环境吧!源码及打包程序的下载链接放在文末!
1.1 开发环境
编程语言:Python 3.12
图形界面库:tkintertools 2.6.21.1(底层为 tkinter)
第三方依赖库:tkintertools 2.6.21.1(就这么一个)
二、程序概览
2.1 代码情况
代码量:1000 行左右
代码大小:34KB
2.2 图片展示
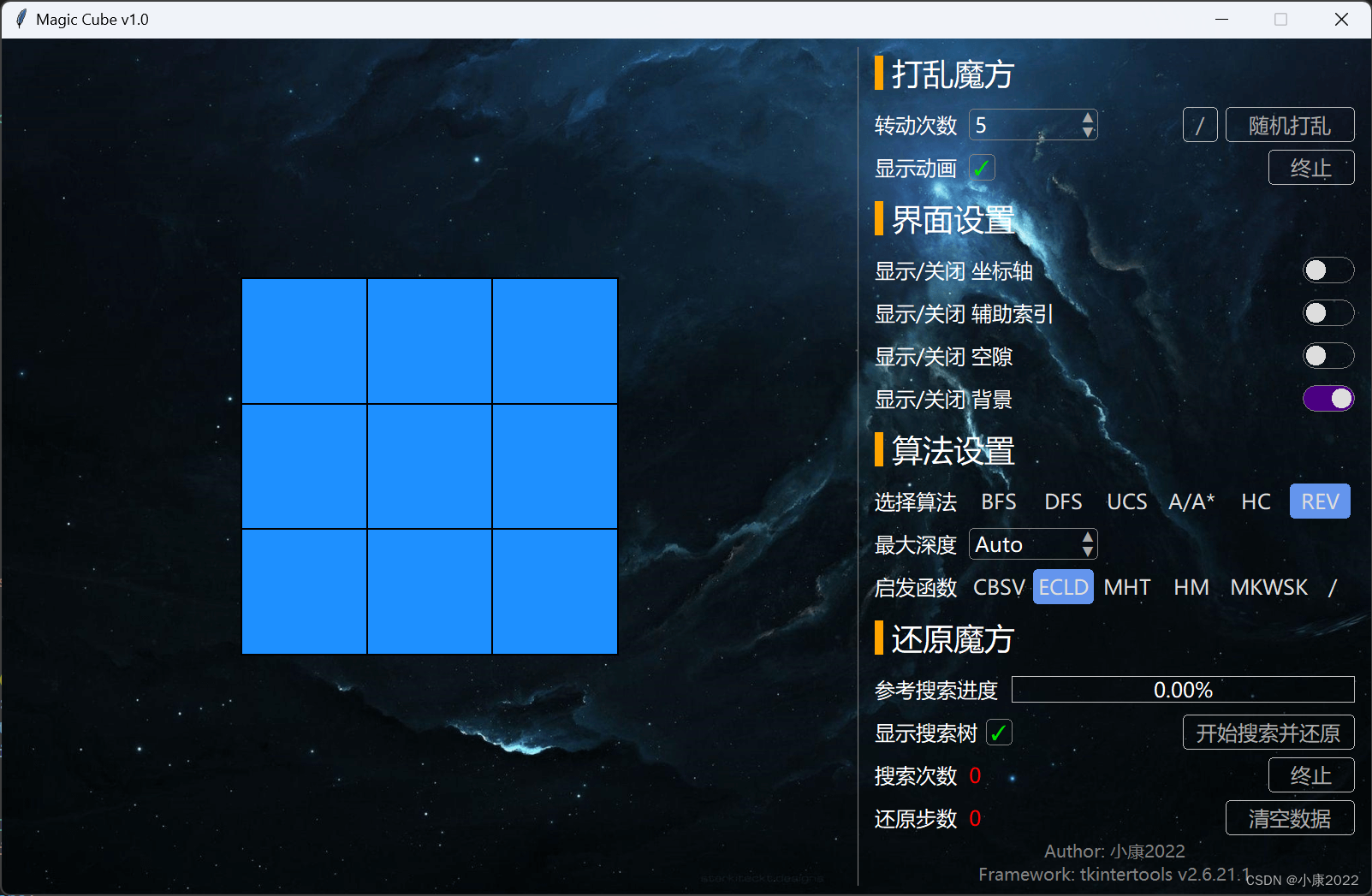
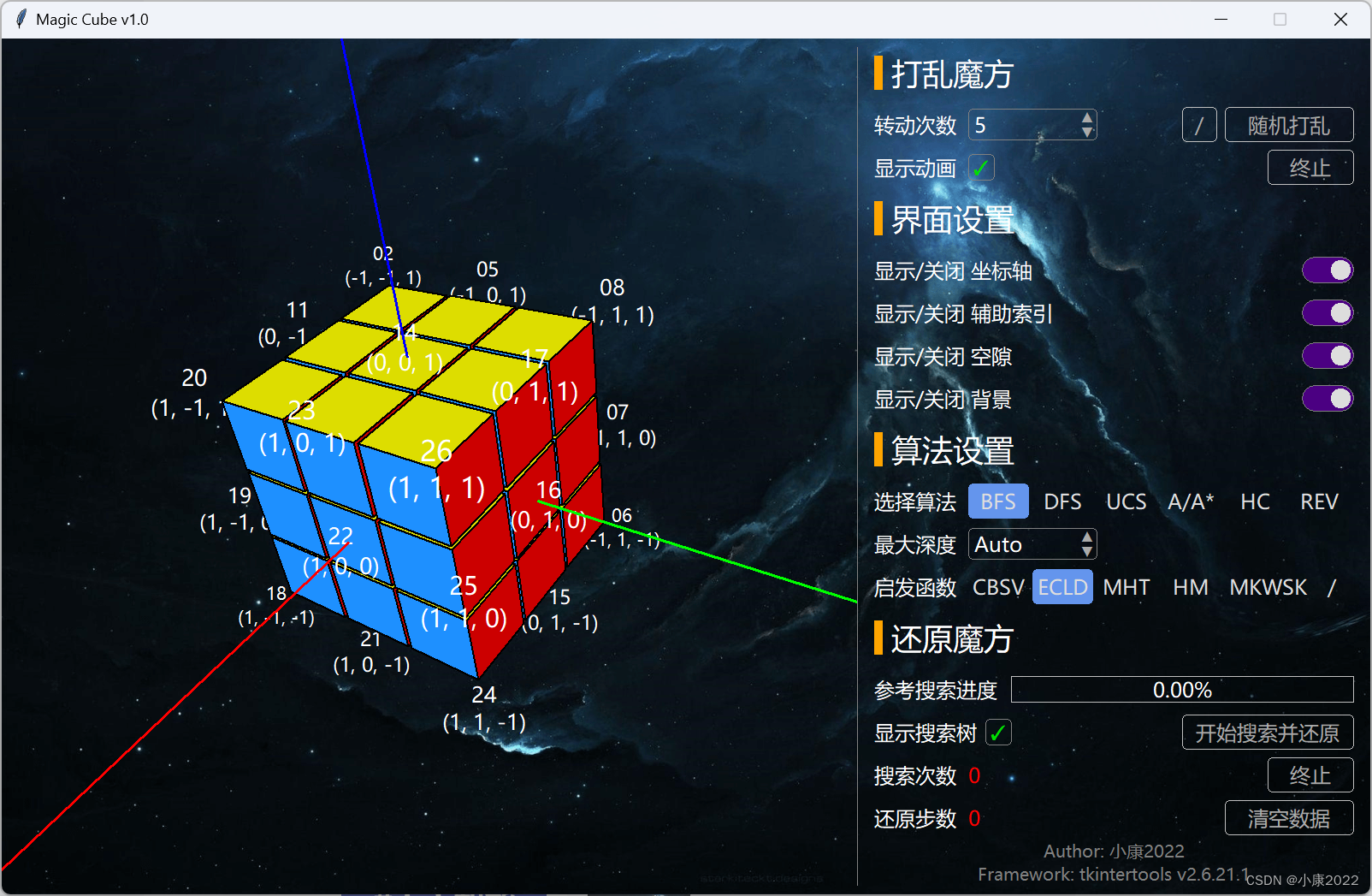

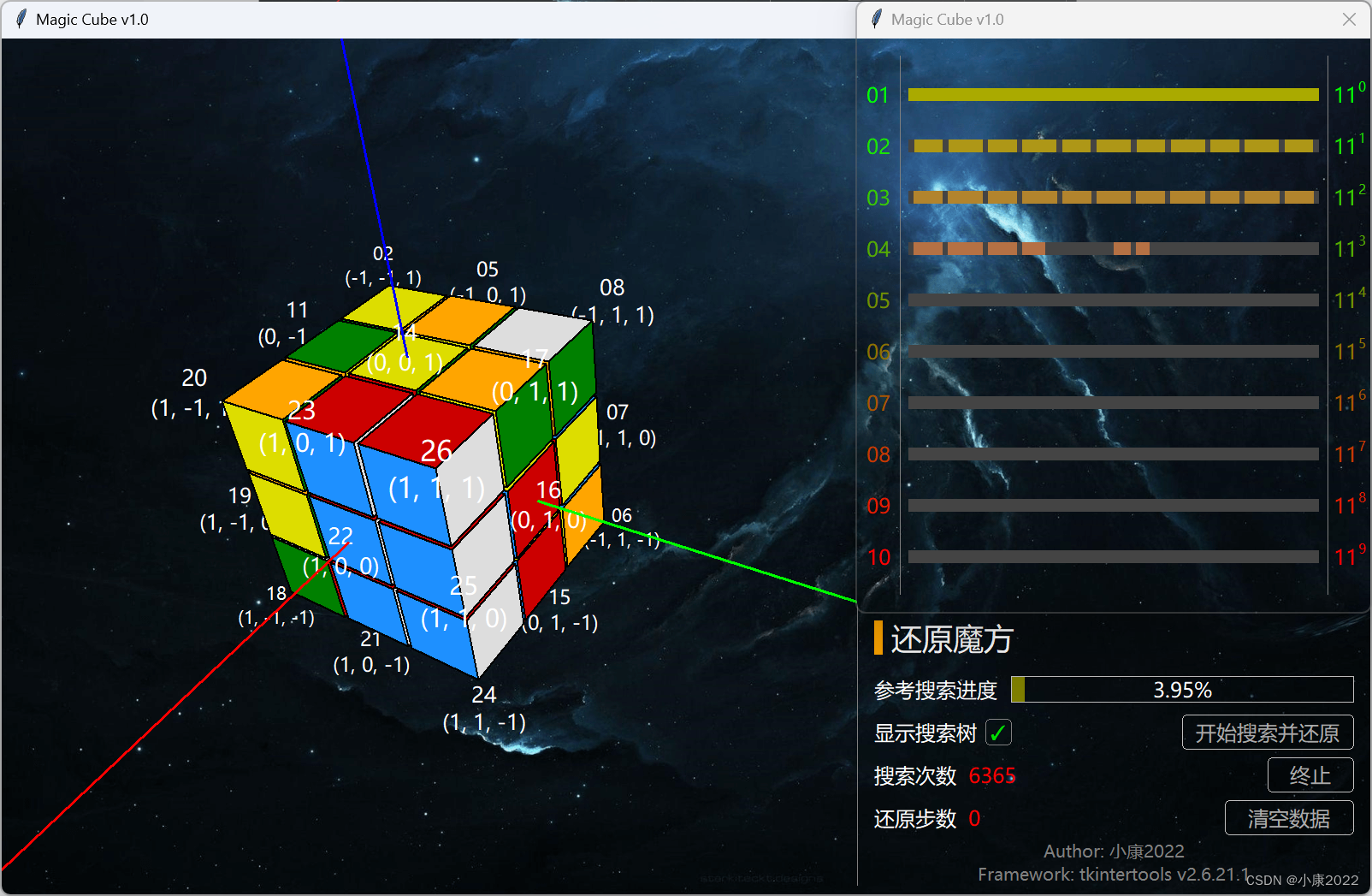

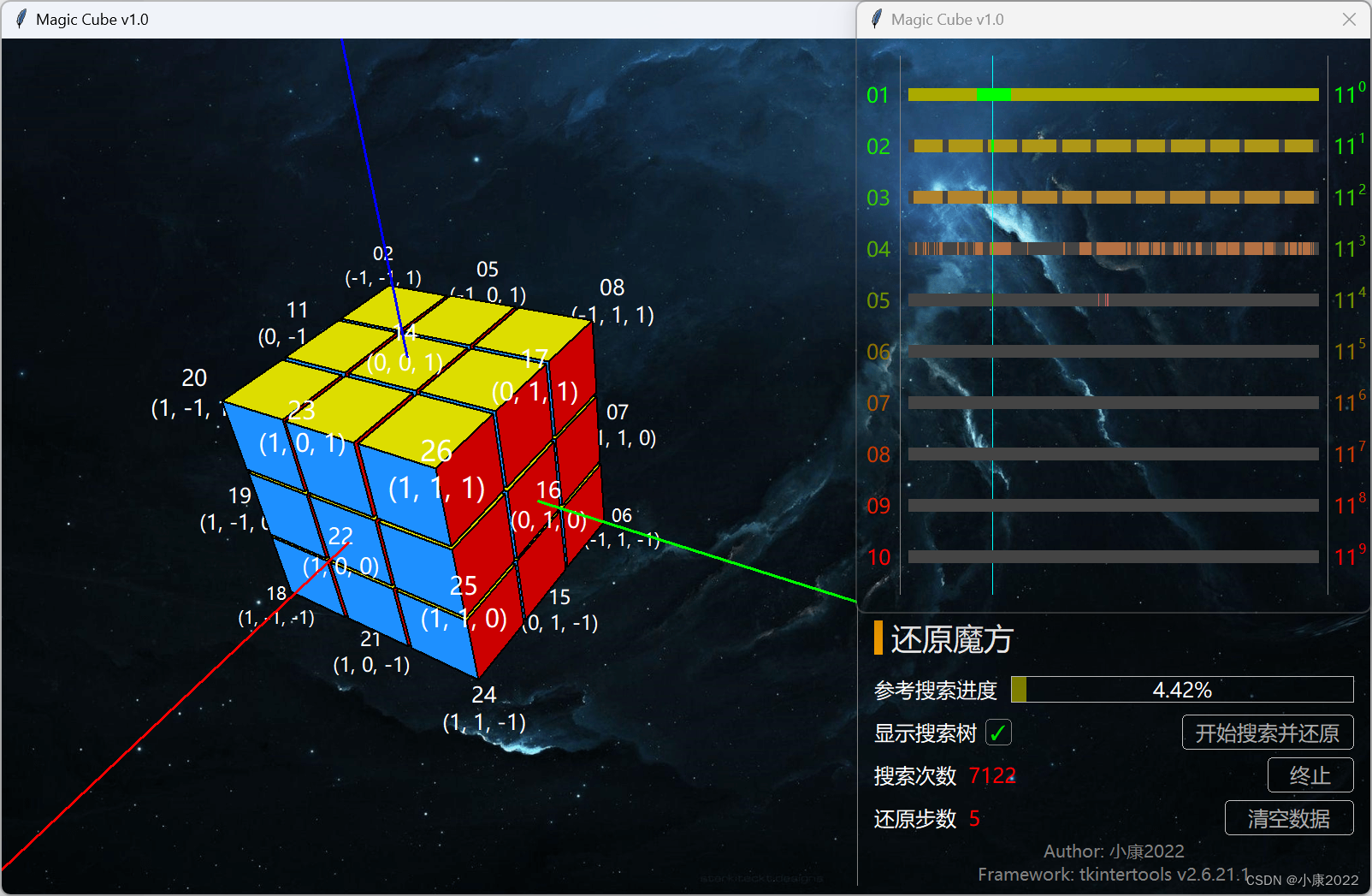
2.3 详细功能
左侧是 3D 显示区,鼠标左键旋转,右键平移,滚轮缩放。
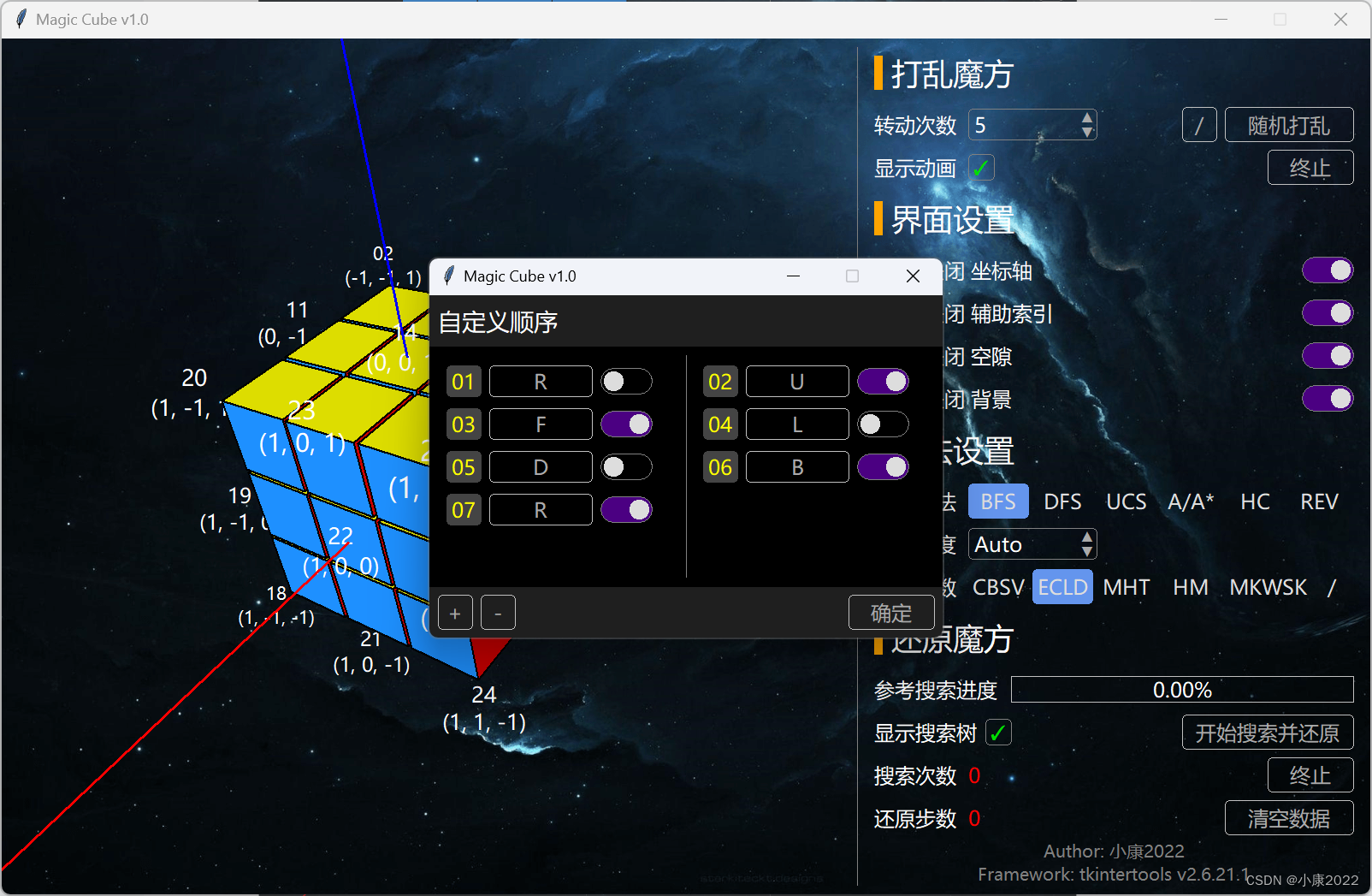
右侧是设定区,点击“开始搜索并还原”时会弹出搜索树弹窗,点击“随机打乱”左边的“/”会弹出“自定义打乱顺序”弹窗。
算法对应表:
| 缩写 | BFS | DFS | UCS | A / A* | HC | REV(测试常用) |
| 说明 | 宽度优先 | 深度优先 | 代价优先 | A 或者 A* 算法 | 爬山法 | 不是算法,逆序还原 |
启发函数对应表:
| 缩写 | CBSV | ECLD | MHT | HM | MKWSK | / |
| 说明 | 切比雪夫距离 | 欧几里得距离 | 曼哈顿距离 | 汉明距离 | 闵可夫斯基距离 | h* |
自定义顺序说明:
每个项目由三个部分组成:编号,方向,旋向
方向对应表:
| 缩写 | R | L | U | D | F | B |
| 说明 | 右(Right) | 左(Left) | 上(Up) | 下(Down) | 前(Front) | 后(Back) |
旋向有两个:顺时针和逆时针,对应开关的两种状态
三、实现过程分析
3.1 状态表示
三阶魔方一共有 3³ =27 个方块,于是使用 1×27 大小的数组来表示每个方块的位置,给它们编号 0~26,当编号与其数组索引一致时,表示魔方为还原状态。
当然,由于魔方的特性,这 27 个位置中有些并不会改变。比如,当操作不涉及中转的时候,有 1+1×6 = 7 个方块永远不会改变位置,而当操作涉及中转的时候,只有中心处方块不会改变位置。为了方便表示,仍然采用整个 1×27 大小的数组表示状态。
3.2 操作方式
分两种情况:
- 当不允许三阶魔方中转的时候,操作共有 6×2 = 12 种,即在魔方 6 个面上顺时针旋转 90°或者逆时针旋转 90°。
- 当允许三阶魔方中转的时候,共有 (6+3)×2 = 18 种,即在第一种情况下加上了三个坐标轴垂直的三个中间面的旋转。
当然,经分析,我认为采用第 1 种情况可能会得到更好结果。
对于第一种情况,魔方将有 1+1×6 = 7 个位置始终固定,使得在完成几乎相同功能的前提下,搜索空间会小一点,且,还原的最终结果只有1个,那就是数组元素与其索引一致。
但反观第二种情况,魔方只有最中间 1 个元素始终固定,在使得搜索空间变大的情况下,还会导致一个程序中不方便处理的问题。因为在这个时候,你会发现,魔方还原的目标状态不只“数组元素与其索引一致”这么一种情况,虽然这可以提高发现目标节点的概率,但搜索空间也变大了,程序实现起来比较麻烦,效率也不见得比第 1 种好。
3.3 启发函数的设计
魔方数据在数组中体现为 1×27,并不方便于直接进行代价的估计,但其在空间上实际是 3×3×3 的,每个方块都有其对应的坐标,于是可以计算每个方块当前位置与目标位置之间的某种差异,并以此作为估计值。
选用的基本启发函数有切比雪夫距离、欧几里得距离、曼哈顿距离和闵可夫斯基距离,同时尝试了一下汉明距离。
不知道什么是切比雪夫距离、欧几里得距离等的朋友,可以去百度一下。
设上述距离对应的启发函数分别为 、
、
、
和
。
其中闵可夫斯基距离拥有可调节的参数 p,我这里动态地根据问题的规模大小设计其值。而汉明距离并非一个空间上的关系,它是从数组的数据上直接进行考虑的,即目标数组与当前数组的差异。
对于上述的启发函数,并非所有都满足可纳性。由于魔方转动一次只能转动一个面,也就是说,方块只能在一个面上移动,对于方块,分两种情况:
- 角方块:每次旋转都是沿坐标方向的,对应曼哈顿距离;
- 边方块:每次旋转都是沿斜直线方向,对应欧几里得距离;
- 面中心方块:始终没有任何移动,计算时不考虑它。
每个面上角方块与边方块各占一半,故 ,但是有:
因此有:
已知,对于闵可夫斯基距离,参数 p=1 时,,参数 p=2 时,
,参数 p=+∞ 时,
,可通过调控其参数 p 来控制其最终效果。
汉明距离并非空间上的距离,属于抽象距离,无法与上面的进行比较。
综上,启发函数为切比雪夫距离、欧几里得距离时,算法为 A* 算法,曼哈顿距离对应的为 A 算法,闵可夫斯基距离是否为 A* 算法与参数 p 有关,汉明距离对应的暂时无法确定。
3.4 算法实现
BFS:用队列实现
DFS:用堆栈实现
UCS:用优先级队列实现,评估函数 F = 代价函数 G
A/A*:用优先级队列实现,评估函数 F = 代价函数 G + 启发函数 H
HC:用优先级队列实现,评估函数 F = 启发函数 H
3.5 结果显示方法
结果采用三种方式进行可视化。
- 搜索之前的打乱魔方与搜索之后的还原魔方通过 3D 魔方实时演示旋转过程;
- 搜索过程之中,通过进度条得知总搜索空间的大小以及当前搜索的空间大小,直观显示其百分占比,并实时显示搜索次数,搜索完成后显示还原步骤的数量;
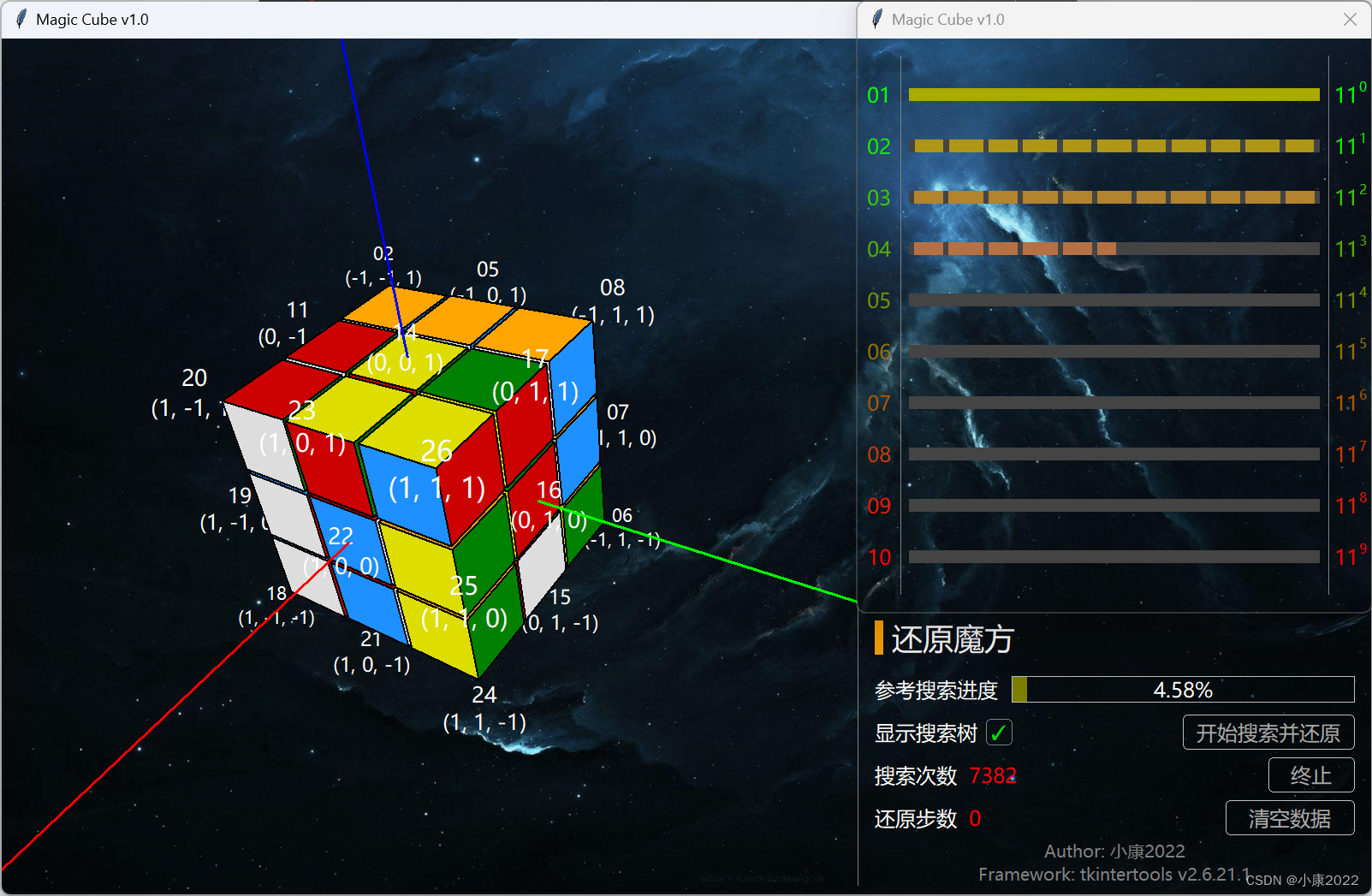
- 搜索过程中实时展示搜索树,由于此数的每层节点数量是指数级增长的,于是就需要将其对数化后以线性的方式的进行展示,层数越大,颜色越深,搜索完毕后标识出搜索路径。
这里说一下为什么实际搜索的状态空间是 11 的 n 次方,而不是 12 的 n 次方,因为每次操作,虽然有 12 步,但实际我们手动不允许它执行与上次转动相反的操作,因为你顺时针转一下,再逆时针转一下,那不等于没转吗?
别小看这点优化,11⁶ = 1771561,12⁶ = 2985984,仅 6 步,相差多少自己看看。
四、写在后面
4.1 开源图形库
本程序使用的 tkintertools 是我自己一个人开发的图形界面库,基于 tkinter,实现了一些 tkinter 没有的功能,里面还有一个可以称为“微型 3D 引擎”的子模块,上述 3D 效果就是这样实现的,此外还提供了较为强大的动画能力,希望大家能支持一下下!
GitHub repo:GitHub - Xiaokang2022/tkintertools
github.io: Profile - 简介 - tkintertools (xiaokang2022.github.io)
4.2 源代码下载
链接文件包含了源代码,以及已经打包好,可以直接运行的 exe 文件。
源代码及打包程序下载链接:Magic Cube v1.2.zip - 蓝奏云
记得给我点赞!收藏!以及在评论区留下你的足迹呀!
相关文章:
多种智能搜索算法可视化还原 3D 魔方
2024/03/19:程序更新说明(文末程序下载链接已更新) 版本:v1.0 → v1.2 ① 修复:将 CLOSED 表内容从优先级队列中分离开来,原优先级队列作 OPEN 表,并用链表树隐式地代替 CLOSED 表,以…...

Maven,pom.xml,查找 子jar包
在IDEA打开pom.xml,会看到这里: 然后如果有需要,把相关的 子jar包 去掉 <dependency><groupId>XXX</groupId><artifactId>XXX</artifactId><exclusions><exclusion><artifactId>xxx</a…...

MySQL中数据库表的监控
MySQL中数据库表的监控 (1)查看数据库中当前打开了哪些表:show OPEN TABLES ,如图6-1-5所示。另外,还可以通过show OPEN TABLES where In_use > 0过滤出当前已经被锁定的表。 查看数据库中表的状态:SHO…...
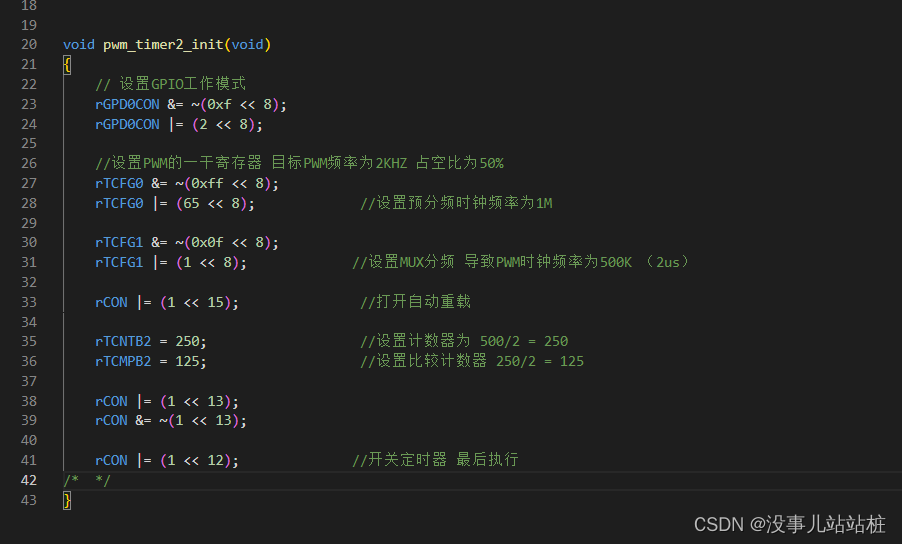
【S5PV210_视频编解码项目】裸机开发2:实现PWM波形驱动蜂鸣器
开发内容介绍 基于芯片自带的PWM定时器模块,实现对PWM波形的控制,掌握pwm定时器的驱动程序开发。 开发理论架构 1)pwm波形的产生的条件:在指定的IO口输出一定频率和占空比的波形 2)pwm波形频率的影响因素࿱…...

js进阶-深入对象-内置构造函数-包装类
一. 创建对象的三种方式 1.1 利用对象字面量创建对象 const p {name:"kebi" }1.2 利用 new Object 创建对象 // const obj new Object()// obj.uname maidi// console.log(obj)const obj new Object({ uname: maidi })1.3 利用构造函数创建对象 大写字母开头的…...

Linux作业
1.创建用户,用户名为user,user02密码均为123.com,创建完成后用tail查看用户是否存在。(截图)(10分) 2.在用户user主目录中用mkdir命令创建目录my.txt,在目录my.txt中创建文件a1.txt、1a1.txt、5…...
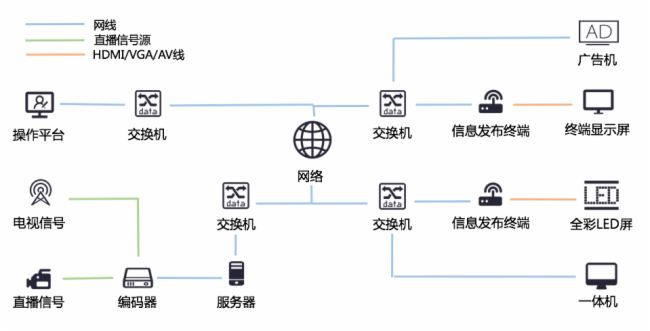
信息发布系统
特色功能 画布功能---可任意拖动各控件的播放位置及大小,可任意选择屏幕背景色或添加背景图 同步联屏---毫秒级同步功能 视频切换无黑屏 触摸查询系统 会议预定系统 终端显示-会议综合屏 终端显示-会议预定屏 终端显示-移动端 广告发布系统 硬件产品-智能终端 硬件…...
Dell Inspiron 戴尔灵越16plus7620升级M2硬盘
主机只支持一条M2硬盘,只能用更换更大容量硬盘的方式增加存储容量。 1、打开后盖,把新硬盘换上。旧硬盘装硬盘盒里,连上主机上。准备一个PE启动U盘, 2、开机不停地按F12,选U盘启动,进入PE,使用…...
视频怎么转mp4格式?分享3个宝藏方法,轻松学会
在当今数字化的时代,视频文件的格式多种多样,而MP4格式因其广泛的兼容性和高质量的压缩技术而备受青睐。然而,有时我们可能需要将其他格式的视频转换为MP4格式,以便在各种设备和平台上播放和分享视频。 在本文中,我们…...
)
Javascript 元二分搜索 | 单边二分查找(Meta Binary Search | One-Sided Binary Search)
元二分搜索(Steven Skiena 在《算法设计手册》第 134 页中也称为单边二分搜索)是二分搜索的一种修改形式,它以增量方式构建数组中目标值的索引。与普通二分搜索一样,元二分搜索需要 O(log n) 时间。 元二分搜索,也称为…...

柚见十三期(优化)
前端优化 加载匹配功能与加载骨架特效 骨架屏 : vant-skeleton index.vue中 /** * 加载数据 */ const loadData async () > { let userListData; loading.value true; //心动模式 if (isMatchMode.value){ const num 10;//推荐人数 userListData await myA…...

Node.js常用命令:了解Node.js的核心命令和用法
学习目标: 理解Node.js和npm的概念及其在开发中的作用;掌握Node.js的核心命令,包括node、npm、npx等;学会使用node命令来执行JavaScript文件和模块;熟悉npm命令,包括安装、更新、卸载依赖包等操作…...

QT 驾校系统界面布局编写
MainWindow::MainWindow(QWidget *parent): QMainWindow(parent), ui(new Ui::MainWindow) {ui->setupUi(this);this->resize(ui->label_img->width(),ui->label_img->height());//图片自适应窗口大小ui->label_img->setScaledContents(true);//图片置…...
【Auth Proxy】为你的 Web 服务上把锁
Auth Proxy 一个极简的用于 Web 服务鉴权的反向代理服务 极其简约的 UI对你的真实服务无任何侵入性支持容器部署,Docker Image 优化到不能再小(不到 9MB)GitHub:https://github.com/wengchaoxi/auth-proxy 效果 我在 http://lo…...
Docker 从0安装 nacos集群
前提条件 Docker支持一下的CentOs版本 Centos7(64-bit),系统内核版本为 3.10 以上Centos6.5(64-bit) 或者更高版本,系统内核版本为 2.6.32-431 或者更高版本 安装步骤 使用 yum 安装(CentOS 7下) 通过 uname -r 命令查看你当…...

keithley2612A数字源表
181/2461/8938产品概述: Keithley 2612A源表既可用作台式I-V表征工具,也可用作多通道I-V测试系统的构建模块组件。对于台式使用,吉时利2612ASourceMeter具有嵌入式TSP Express软件工具,允许用户快速轻松地执行常见的I-V测试&…...

AI助手 - 月之暗面 Kimi.ai
前言 这是 AI工具专栏 下的第四篇,这一篇所介绍的AI,也许是截至今天(204-03-19)国内可访问的实用性最强的一款。 今年年初,一直看到有人推荐 Kimi,不过面对雨后春笋般的各类品质的AI,说实话也有…...

《计算机考研精炼1000题》为你考研之路保驾护航
创作背景 在这个充满挑战与竞争的时代,每一位考生在备战研究生考试的过程中,都希望通过更多符合考纲要求的练习题来提高自己的知识和技能。为了满足这一需求,我们精心策划和编辑了这本《计算机考研精炼1000题》。在考研政治和考研数学领域&a…...

el-input添加keyup事件无响应
<el-input type"password" v-model"formData.password" keyup.enter"onSubmit"></el-input>使用 .native修饰符 有时,Vue 组件内部可能会处理某些事件,导致你不能直接在组件上监听这些事件。 在这种情况下&am…...

错误1075:依存服务不存在, 或已标记为删除的解决方法
错误1075:依存服务不存在, 或已标记为删除的解决方法 运行 sc config spooler depend rpcss 注意"depend “而不是"depend”。...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...

在ubuntu等linux系统上申请https证书
使用 Certbot 自动申请 安装 Certbot Certbot 是 Let’s Encrypt 官方推荐的自动化工具,支持多种操作系统和服务器环境。 在 Ubuntu/Debian 上: sudo apt update sudo apt install certbot申请证书 纯手动方式(不自动配置)&…...

【Linux应用】Linux系统日志上报服务,以及thttpd的配置、发送函数
【Linux应用】Linux系统日志上报服务,以及thttpd的配置、发送函数 文章目录 thttpd服务安装thttpd配置thttpd服务thttpd函数日志效果和文件附录:开发板快速上手:镜像烧录、串口shell、外设挂载、WiFi配置、SSH连接、文件交互(RADX…...
