Educational Codeforces Round 163 (Rated for Div. 2)(A,B,C,D,E)
比赛链接
好忙好忙好忙,慢慢补老比赛的题解了。
这场没啥算法,全是思维。有也是BFS,屎。
A. Special Characters
题意:
您将得到一个整数 n n n 。
您的任务是构建一串大写的拉丁字母。此字符串中必须正好有 n n n 个特殊字符。让我们称一个字符为特殊字符,如果它恰好等于它的一个邻居。
例如,AAABAACC字符串中有 6 6 6 个特殊字符(位置为: 1 1 1 、 3 3 3 、 5 5 5 、 6 6 6 , 7 7 7 和 8 8 8 )。
打印任何合适的字符串或报告没有这样的字符串。
思路:
发现如果是 AABBAABB 这样子的序列的话,每个字符都会是特殊字符。但是这样的只能构造出 n n n 为偶数时候的情况。考虑能否构造出 n n n 为奇数时候的情况。
因为一个字符为特殊字符只和它的左右相邻的字符有关,再往前是什么它是不在意的。所以我们构造 n n n 为奇数时候的情况时,前面的部分仍然用类似 AABB 这种形式来构造,因为三个及以上连续的字符挨在一起时,中间的字符就不是特殊字符,不会产生贡献了,只有两头的字符会产生贡献,它就和两个字符的等价,所以我们不妨规定挨在一起的相同字符最多有两个。
于是,如果前面的部分结尾为 A A AA AA 时,我们后面会补上 B B B,这时这个 B B B 不是特殊字符,因此这时凑不出奇数情况。然后我们继续向后补字符,如果我们补 A A A,这个 A A A 也不是特殊字符,凑不出奇数情况,如果补 B B B,这时补的两个 B B B 都同时成为了特殊字符,相当于上面说的 A A B B AABB AABB 形式,仍然凑不出奇数情况。
如果我们在补上 B A BA BA,然后继续向后补字符,就会重复上面的讨论。因此无论怎么补,我们都凑不出奇数情况。这就意味着 n n n 为奇数时是无解的。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=55;int T,n;
char s[maxn];int main(){cin>>T;while(T--){cin>>n;if(n&1){cout<<"NO"<<endl;continue;}else cout<<"YES"<<endl;for(int i=1;i<=n;i+=4)s[i]=s[i+1]='A';for(int i=3;i<=n;i+=4)s[i]=s[i+1]='B';for(int i=1;i<=n;i++)cout<<s[i];cout<<endl;}return 0;
}
B. Array Fix
题意:
您将得到一个长度为 n n n 的整数数组 a a a 。
您可以执行以下操作任意次数(可能为零):取数组 a a a 中至少为 10 10 10 的任何元素,将其删除,然后在相同位置插入该元素所包含的数字,按它们出现在该元素中的顺序。例如:
-
如果我们将此操作应用于数组 [ 12 , 3 , 45 , 67 ] [12, 3, 45, 67] [12,3,45,67] 的第 3 3 3 个元素,则数组将变为 [ 12 , 3 , 4 , 5 , 67 ] [12, 3, 4, 5, 67] [12,3,4,5,67] 。
-
如果我们将此操作应用于数组 [ 2 , 10 ] [2, 10] [2,10] 的第 2 2 2 个元素,则数组将变为 [ 2 , 1 , 0 ] [2, 1, 0] [2,1,0] 。
您的任务是确定是否可以使用上述操作任意次数使 a a a 按非降序排序。换句话说,您必须确定是否可以将数组 a a a 转换为 a 1 ≤ a 2 ≤ ⋯ ≤ a k a_1 \le a_2 \le \dots \le a_k a1≤a2≤⋯≤ak ,其中 k k k 是数组 a a a 的当前长度。
思路:
先注意一下题目说了 0 ≤ a i ≤ 99 0 \le a_i \le 99 0≤ai≤99,因此 a i a_i ai 最多就是个两位数。
因为是非降序的,所以从某一位开始,也许后面就都变成了两位及以上的数,这时这些数不能被拆数位,否则变成一位数之后就会变小。反之,在此之前,所有的数都得是一位数,否则某个两位数后面出现了一位数,就不满足非降序的条件了。因此我们找到这个分界点,把分界点之前的所有数都拆掉,然后看满不满足条件就行了。
根据上面的分析,这个分界点之后的数都是不拆数位就满足非降序的,所以我们从后向前找到第一个不满足条件的位置,这个位置就是分界点了。从这个位置向前拆数。一个数拆开后,个位放在后面,十位放在前面。所以我们没必要真的把两个新的数插入到当前位置,这样比较麻烦。
判断这个数是否和后一个数满足非降序的关系,我们直接看一下当前数的十位不小于个位,并且个位不小于后一个数,之后用十位代替这个数,再向前找即可。
code:
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=55;int T,n,a[maxn];int main(){cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];int idx;for(idx=n-1;idx>=1;idx--)if(a[idx]>a[idx+1])break;// cout<<"***"<<idx<<endl;bool flag=true;for(int i=idx;i>=1;i--){if(a[i]/10>a[i]%10 || a[i]%10>a[i+1]){flag=false;break;}if(a[i]>10)a[i]/=10;}puts((flag)?"YES":"NO");}return 0;
}
C. Arrow Path
题意:
有一个网格,由 2 2 2 行和 n n n 列组成。这些行从上到下从 1 1 1 到 2 2 2 进行编号。列从左到右从 1 1 1 到 n n n 进行编号。网格的每个单元格都包含一个指向左侧或右侧的箭头。没有箭头指向网格外。
有一个机器人在单元格 ( 1 , 1 ) (1, 1) (1,1) 中启动 。每一秒钟,都有以下两个动作相继发生:
-
首先,机器人向左、向右、向下或向上移动(它不能尝试走出网格,也不能跳过这次移动)
-
然后,它沿着放置在当前单元格(移动后结束的单元格)中的箭头移动。
您的任务是确定机器人是否可以到达单元 ( 2 , n ) (2, n) (2,n) 。
思路:
比较明显的BFS。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>
#define pii pair<int,int>
using namespace std;
const int maxn=2e5+5;int T,n;
string mp[5];int fx[]={1,-1,0,0},fy[]={0,0,1,-1};int main(){cin>>T;while(T--){cin>>n;cin>>mp[1]>>mp[2];mp[1]=" "+mp[1];mp[2]=" "+mp[2];queue<pii> q;vector<vector<bool> > vis(5,vector<bool>(n+5,false));q.push(pii(1,1));vis[1][1]=true;bool flag=false;while(!q.empty()){int ux=q.front().first,uy=q.front().second;q.pop();if(ux==2 && uy==n){flag=true;break;}for(int i=0,x,y;i<4;i++){x=ux+fx[i],y=uy+fy[i];if(x<1 || x>2 || y<1 || y>n)continue;if(mp[x][y]=='<')y--;else y++;if(!vis[x][y]){q.push(pii(x,y));vis[x][y]=true;}}}puts((flag)?"YES":"NO");}return 0;
}
D. Tandem Repeats?
题意:
您将得到一个字符串 s s s ,它由小写的拉丁字母以及问号组成。
串联重复序列(tandem repeat)是指长度为偶数的串,满足其前一半等于其后一半。
您的目标是将每个问号替换为某个小写拉丁字母,求出最大可能的串联重复序列子串的长度。
思路:
考虑到这个串联重复序列比如 a b c a b c abcabc abcabc,说白了就是第 1 1 1 个字符向后 3 3 3 个长度的子串与第 4 4 4 个字符向后 3 3 3 个长度的子串相同。那么一定第 2 2 2 个字符向后 2 2 2 个长度的子串与第 5 5 5 个字符向后 2 2 2 个长度的子串相同,前者可以由后者推出来。
所以我们设 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示从第 i i i 个字符开始的子串和第 j j j 个字符开始的子串最长匹配长度是多少。当第 i i i 个字符和第 j j j 个字符相同时(两个字符真的相同,或者其中一个为 ? ? ?,可以万能匹配), d p [ i ] [ j ] dp[i][j] dp[i][j] 就可以从 d p [ i + 1 ] [ j + 1 ] + 1 dp[i+1][j+1]+1 dp[i+1][j+1]+1 推过来。因为是从 i + 1 , j + 1 i+1,j+1 i+1,j+1 推来的,因此 i , j i,j i,j 的枚举需要反着,从 n n n 到 1 1 1。
不过 i ∼ i + d p [ i ] [ j ] − 1 i\sim i+dp[i][j]-1 i∼i+dp[i][j]−1 与 j ∼ j + d p [ i ] [ j ] − 1 j\sim j+dp[i][j]-1 j∼j+dp[i][j]−1 两个区间的子串匹配不一定就是串联重复序列,它需要正好是 i + d p [ i ] [ j ] − 1 = j − 1 i+dp[i][j]-1=j-1 i+dp[i][j]−1=j−1 即 j − i = d p [ i ] [ j ] j-i=dp[i][j] j−i=dp[i][j](也就是前后两个子串正好相接)。 d p [ i ] [ j ] dp[i][j] dp[i][j] 如果大于 j − i j-i j−i,这时可以直接截取长为 j − i j-i j−i 的一段作为串联重复序列,反之就一定无法成为串联重复序列。
code:
#include <cstdio>
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;int T,n;
string s;int main(){cin>>T;while(T--){cin>>s;n=s.length();s=" "+s;vector<vector<int> > dp(n+5,vector<int>(n+5,0));for(int i=n;i>=1;i--){for(int j=i-1;j>=1;j--){if(s[i]=='?' || s[j]=='?' || s[i]==s[j])dp[i][j]=dp[i+1][j+1]+1;}}int ans=0;for(int i=1;i<=n;i++){for(int j=1;j<i;j++){int t=dp[i][j];if(t>=i-j)t=i-j;else continue;ans=max(ans,t);}}cout<<ans*2<<endl;}return 0;
}
E. Clique Partition
题意:
给出两个整数 n n n 和 k k k 。在 n n n 个顶点上有一个图,编号从 1 1 1 到 n n n ,它最初没有边。你必须给每个顶点分配一个整数,设 a i a_i ai 是顶点 i i i 上的整数。所有 a i a_i ai 都应该是从 1 1 1 到 n n n 的不同整数。
指定整数后,对于每对顶点 ( i , j ) (i, j) (i,j) ,如果 ∣ i − j ∣ + ∣ a i − a j ∣ ≤ k |i - j| + |a_i - a_j| \le k ∣i−j∣+∣ai−aj∣≤k ,则在它们之间添加一条边。
您的目标是创建一个图,该图可以划分为最小可能(对于给定的 n n n 和 k k k 值)数量的团(Clique)。
图的每个顶点应该恰好属于一个团。
团是一组顶点,其中的每一对顶点都与一条边相连。由于布莱德斯特没有真正提高他的编程技能,他无法解决问题 “给一个图,将其划分为最小数量的团”。因此,我们要求您打印分区本身。
思路:
构造题,构造方法不好想。如果想出了构造方法,写是比较容易的。
要团的个数最少,那么就考虑让团包含的点最多。因为 a i a_i ai 互不重复,所以 ∣ a i − a j ∣ |a_i - a_j| ∣ai−aj∣ 至少会是 1 1 1,那么 ∣ i − j ∣ |i - j| ∣i−j∣ 最大就是 k − 1 k-1 k−1,这时 j − i + 1 j-i+1 j−i+1 最大就是 k k k。也就是说,团最多可能包含 k k k 个点。
考虑如果一个团能否塞入 k k k 个点,不妨使用顶点 1 ∼ k 1\sim k 1∼k。而且为了不影响到其他团,所以我们尽量给它们分配 1 ∼ k 1\sim k 1∼k 的编号。
首先第 1 1 1 个数和第 k k k 个数必须差 1 1 1,否则这一对一定不满足条件。同理,第 1 1 1 个数和第 k − 1 k-1 k−1 个数必须差 ≤ 2 \le 2 ≤2,第 2 2 2 个数和第 k k k 个数必须差 ≤ 2 \le 2 ≤2。考虑把第一个数置为中间数 k / 2 k/2 k/2,这样中间数两边都有空间,我们把中间数前面的数降序放在前半部分,中间数后面的数降序放在后半部分。即: k / 2 , k / 2 − 1 , … , 1 , k , k − 1 … , k / 2 + 2 , k / 2 + 1 k/2,k/2-1,\dots,1,k,k-1\dots,k/2+2,k/2+1 k/2,k/2−1,…,1,k,k−1…,k/2+2,k/2+1
还是比较好验证这么构造的正确性的:前半部分一定满足条件,后半部分一定满足条件。前半部分取一个数,后半部分取一个数的情况也满足条件。综合一下,所有情况都满足条件。
这样 1 ∼ k 1\sim k 1∼k 的情况就构造出来了,因为相对位置和相对大小是不变的,所以后面的每个团也是这样构造就可以了。
有时候会剩下一些点不足 k k k 个。构造方式同理,把上面的序列截掉后面部分即可,大概就是这样:
- 如果 n ≤ k / 2 n\le k/2 n≤k/2,则 n , n − 1 , … , 1 n,n-1,\dots,1 n,n−1,…,1
- 如果 k / 2 < n < k k/2\lt n\lt k k/2<n<k,则 k / 2 , k / 2 − 1 , … , 1 , n , n − 1 … , k / 2 + 2 , k / 2 + 1 k/2,k/2-1,\dots,1,n,n-1\dots,k/2+2,k/2+1 k/2,k/2−1,…,1,n,n−1…,k/2+2,k/2+1
团的个数也就很显然了,是 ⌈ n k ⌉ \left\lceil\dfrac nk\right\rceil ⌈kn⌉。第 i i i 个点所属的团显然就是第 ⌈ i k ⌉ \left\lceil\dfrac ik\right\rceil ⌈ki⌉ 个团。
code:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn=45;int T,n,k;
int a[maxn];int main(){cin>>T;while(T--){cin>>n>>k;for(int i=1,len=k;i<=n;i+=k){if(i+k-1<=n){for(int j=i;j<i+len;j++)a[j]=j;reverse(a+i,a+i+len/2);reverse(a+i+len/2,a+i+len);}else {if(i+len/2>=n){for(int j=i;j<=n;j++)a[j]=j;reverse(a+i,a+n+1);}else {for(int j=i;j<=n;j++)a[j]=j;reverse(a+i,a+i+len/2);reverse(a+i+len/2,a+n+1);}}}
// cout<<"***";for(int i=1;i<=n;i++)printf("%d ",a[i]);puts("");cout<<(n+k-1)/k<<endl;for(int i=1;i<=n;i++){printf("%d ",(i+k-1)/k);}puts("");}return 0;
}
相关文章:
(A,B,C,D,E))
Educational Codeforces Round 163 (Rated for Div. 2)(A,B,C,D,E)
比赛链接 好忙好忙好忙,慢慢补老比赛的题解了。 这场没啥算法,全是思维。有也是BFS,屎。 A. Special Characters 题意: 您将得到一个整数 n n n 。 您的任务是构建一串大写的拉丁字母。此字符串中必须正好有 n n n 个特殊字…...
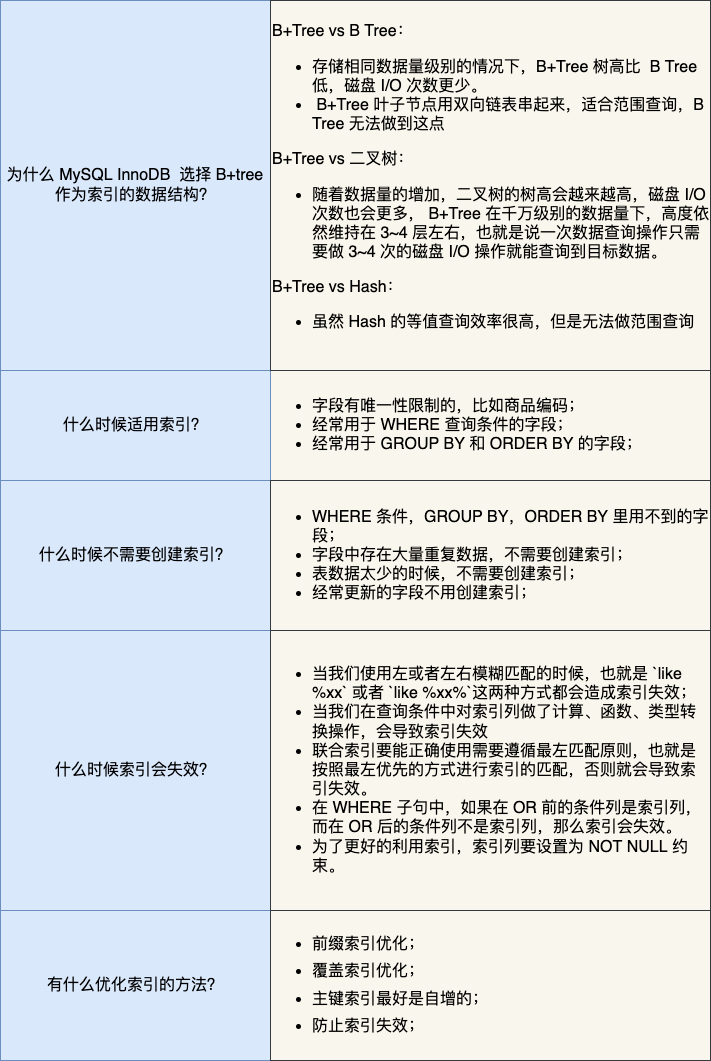
索引常见面试题
面试中,MySQL 索引相关的问题基本都是一系列问题,都是先从索引的基本原理,再到索引的使用场景,比如: 索引底层使用了什么数据结构和算法?为什么 MySQL InnoDB 选择 Btree 作为索引的数据结构?什…...

【Unity】旋转的尽头是使用四元数让物体旋转
// 导入必要的命名空间 using System.Collections; using System.Collections.Generic; using UnityEngine;// 创建一个名为 RotateObj 的 MonoBehaviour 类,该类可以附加到 Unity 中的游戏对象上并控制其行为 public class RotateObj : MonoBehaviour {// Update 函…...
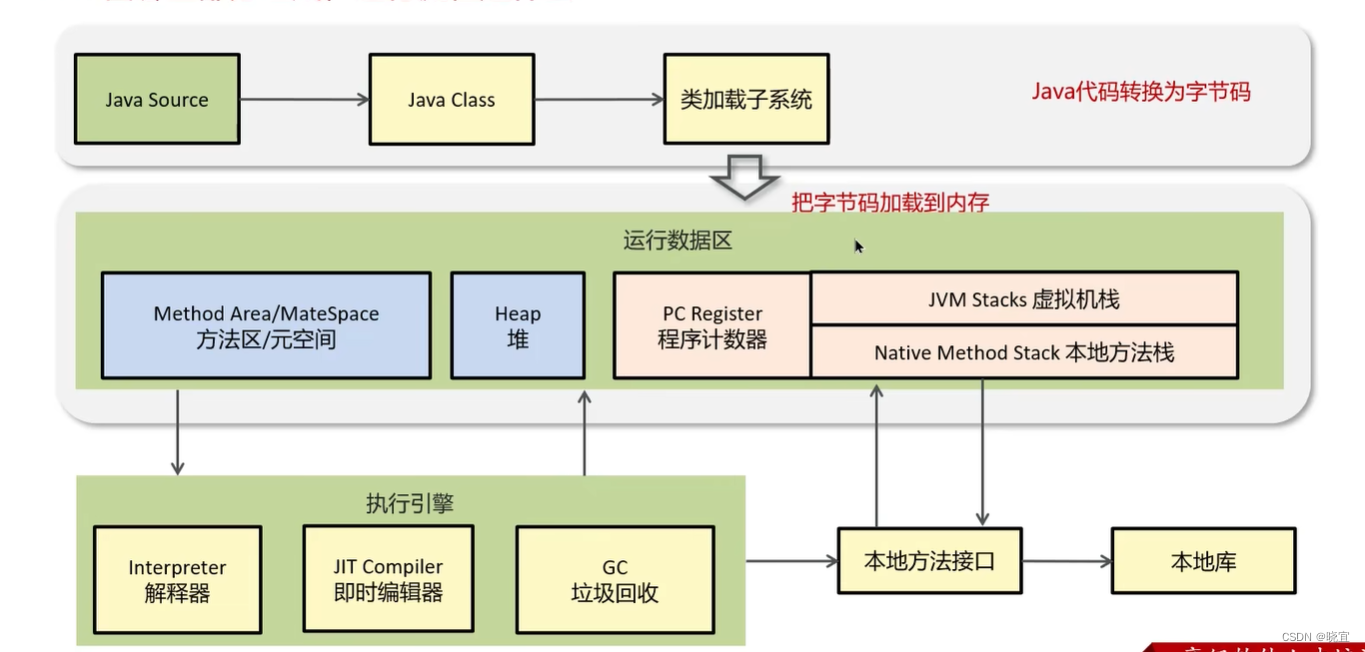
哔哩哔哩秋招Java二面
前言 作者:晓宜 个人简介:互联网大厂Java准入职,阿里云专家博主,csdn后端优质创作者,算法爱好者 一面过后面试官叫我别走,然后就直接二面,二面比较简短,记录一下,希望可以…...

OSPF特殊区域(stub\nssa)
stub区域——只有1类、2类、3类;完全stub区域——只有1类、2类 NSSA区域:本区域将自己引入的外部路由发布给其他区域,但不需要接收其他区域的路由 在NSSA区域的路由器上,引入外部路由时,不会转换成5类LSA,…...

全球首位AI程序员诞生,将会对程序员的影响有多大?
随着全球首位AI程序员Devin的诞生,人工智能技术在编程领域的应用引发了广泛的讨论和思考。这一事件不仅标志着AI技术在软件开发领域的一大步进展,也引起了人们对未来编程职业发展的广泛关注。那么,AI程序员的出现究竟会对程序员的职业生涯产生…...

【晴问算法】提高篇—动态规划专题—最长上升子序列
题目描述 现有一个整数序列a1,a2,...,an,求最长的子序列(可以不连续),使得这个子序列中的元素是非递减的。输出该最大长度。 输入描述 第一行一个正整数n(1≤n≤100),表示序…...
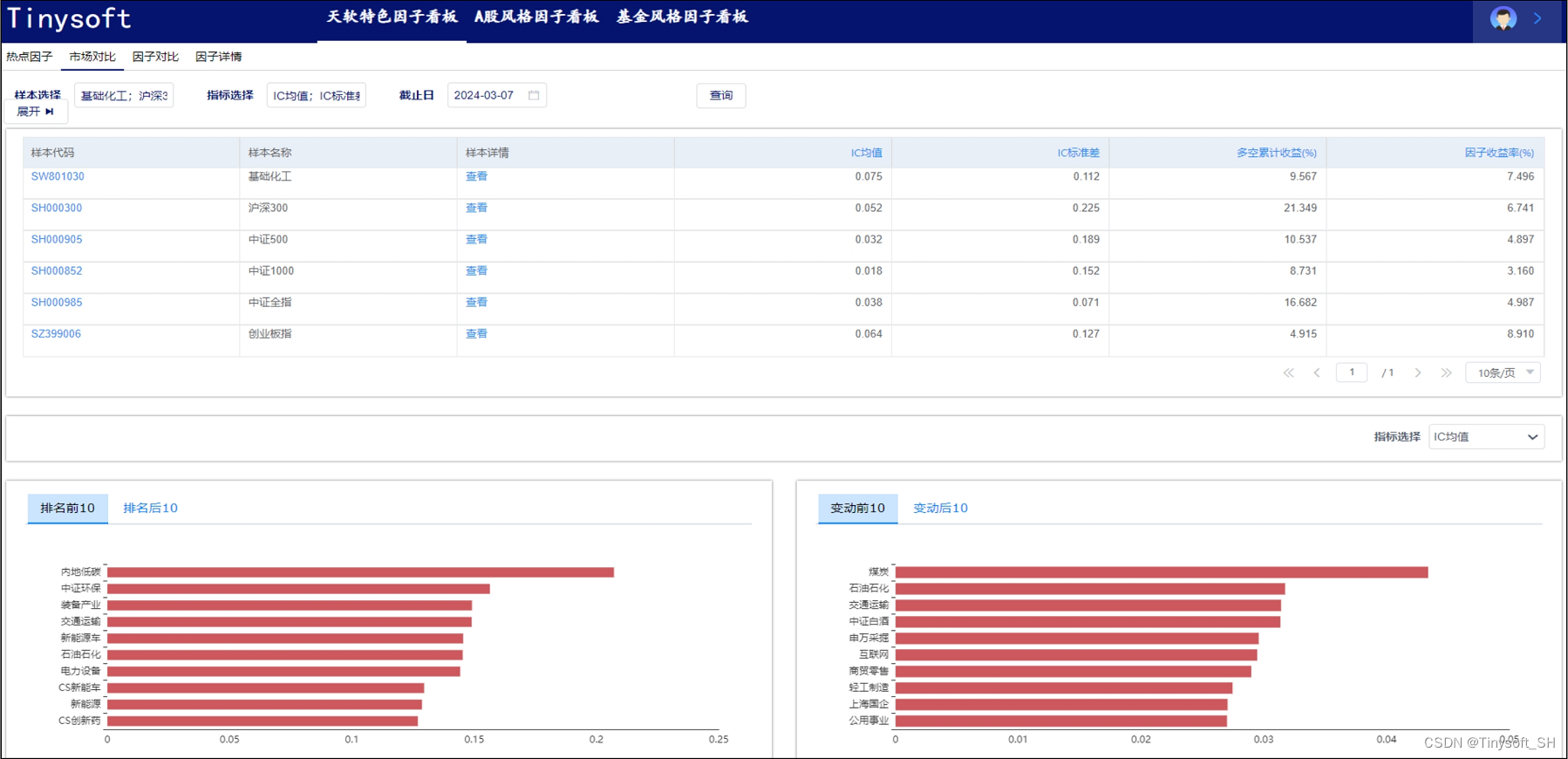
天软特色因子看板(2024.3第5期)
该因子看板跟踪天软特色因子A08006(近一月日度买卖压力2),该因子为近一个月个股每日的相对价格位置,用以刻画股票所受买卖压力,取作 介于0~1间,指标值越大,反映股票在价格相对高位停留的时间越长,所面临的买…...

静态网络配置
一、查看网络命令 1.命令行查看网络配置 1、查看ip\硬件设备-网卡 ifconfig -a ifconfig ens160 网卡名称 ip addr show ip addr show ens160 nmcli device show ens160 nmcli con up ens160 2、主机名称 hostname hostname hfj.huaxia.com 3、查看路由和网关 rou…...
多种智能搜索算法可视化还原 3D 魔方
2024/03/19:程序更新说明(文末程序下载链接已更新) 版本:v1.0 → v1.2 ① 修复:将 CLOSED 表内容从优先级队列中分离开来,原优先级队列作 OPEN 表,并用链表树隐式地代替 CLOSED 表,以…...

Maven,pom.xml,查找 子jar包
在IDEA打开pom.xml,会看到这里: 然后如果有需要,把相关的 子jar包 去掉 <dependency><groupId>XXX</groupId><artifactId>XXX</artifactId><exclusions><exclusion><artifactId>xxx</a…...

MySQL中数据库表的监控
MySQL中数据库表的监控 (1)查看数据库中当前打开了哪些表:show OPEN TABLES ,如图6-1-5所示。另外,还可以通过show OPEN TABLES where In_use > 0过滤出当前已经被锁定的表。 查看数据库中表的状态:SHO…...
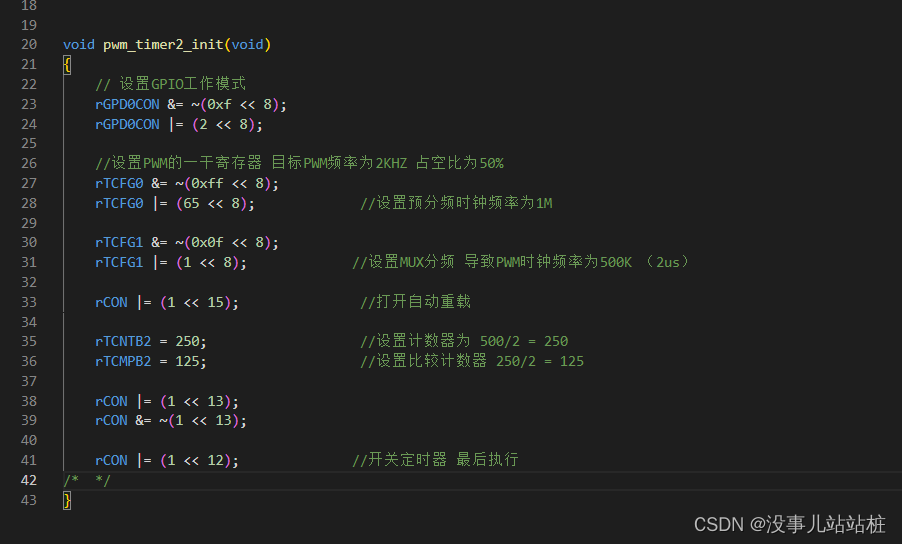
【S5PV210_视频编解码项目】裸机开发2:实现PWM波形驱动蜂鸣器
开发内容介绍 基于芯片自带的PWM定时器模块,实现对PWM波形的控制,掌握pwm定时器的驱动程序开发。 开发理论架构 1)pwm波形的产生的条件:在指定的IO口输出一定频率和占空比的波形 2)pwm波形频率的影响因素࿱…...

js进阶-深入对象-内置构造函数-包装类
一. 创建对象的三种方式 1.1 利用对象字面量创建对象 const p {name:"kebi" }1.2 利用 new Object 创建对象 // const obj new Object()// obj.uname maidi// console.log(obj)const obj new Object({ uname: maidi })1.3 利用构造函数创建对象 大写字母开头的…...

Linux作业
1.创建用户,用户名为user,user02密码均为123.com,创建完成后用tail查看用户是否存在。(截图)(10分) 2.在用户user主目录中用mkdir命令创建目录my.txt,在目录my.txt中创建文件a1.txt、1a1.txt、5…...
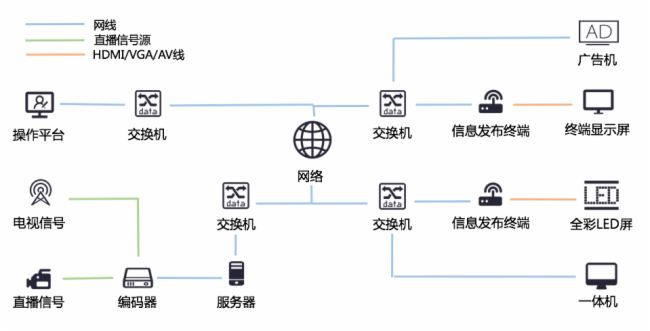
信息发布系统
特色功能 画布功能---可任意拖动各控件的播放位置及大小,可任意选择屏幕背景色或添加背景图 同步联屏---毫秒级同步功能 视频切换无黑屏 触摸查询系统 会议预定系统 终端显示-会议综合屏 终端显示-会议预定屏 终端显示-移动端 广告发布系统 硬件产品-智能终端 硬件…...
Dell Inspiron 戴尔灵越16plus7620升级M2硬盘
主机只支持一条M2硬盘,只能用更换更大容量硬盘的方式增加存储容量。 1、打开后盖,把新硬盘换上。旧硬盘装硬盘盒里,连上主机上。准备一个PE启动U盘, 2、开机不停地按F12,选U盘启动,进入PE,使用…...
视频怎么转mp4格式?分享3个宝藏方法,轻松学会
在当今数字化的时代,视频文件的格式多种多样,而MP4格式因其广泛的兼容性和高质量的压缩技术而备受青睐。然而,有时我们可能需要将其他格式的视频转换为MP4格式,以便在各种设备和平台上播放和分享视频。 在本文中,我们…...
)
Javascript 元二分搜索 | 单边二分查找(Meta Binary Search | One-Sided Binary Search)
元二分搜索(Steven Skiena 在《算法设计手册》第 134 页中也称为单边二分搜索)是二分搜索的一种修改形式,它以增量方式构建数组中目标值的索引。与普通二分搜索一样,元二分搜索需要 O(log n) 时间。 元二分搜索,也称为…...

柚见十三期(优化)
前端优化 加载匹配功能与加载骨架特效 骨架屏 : vant-skeleton index.vue中 /** * 加载数据 */ const loadData async () > { let userListData; loading.value true; //心动模式 if (isMatchMode.value){ const num 10;//推荐人数 userListData await myA…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
