算法打卡day21|回溯法篇01|理论知识,Leetcode 77.组合
回溯法理论知识
回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。所以回溯函数也就是递归函数,指的都是一个函数。
回溯法的效率
回溯法并不是什么高效的算法。因为回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,如果想让回溯法高效一些,可以加一些剪枝的操作,但也改不了回溯法就是穷举的本质。
既然回溯法并不高效为什么还要用它呢?因为没得选,一些问题能暴力搜出来就不错了,撑死了再剪枝一下,还没有更高效的解法。
回溯法解决的问题
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
以上每个问题,都不简单!
如何理解回溯法
回溯法解决的问题都可以抽象为树形结构。因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,都构成的树的深度。递归就要有终止条件,所以必然是一棵高度有限的树(N叉树)。
回溯法模板
这里给出卡哥总结的回溯算法模板。
回溯三部曲:
1.回溯函数模板返回值以及参数
在回溯算法中,函数起名字为backtracking,回溯算法中函数返回值一般为void。
再来看一下参数,因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来,所以一般是先写逻辑,然后需要什么参数,就填什么参数。
2.回溯函数终止条件
既然是树形结构,遍历树形结构一定要有终止条件。一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
3.回溯搜索的遍历过程
回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。
for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了。
分析完过程,回溯算法模板框架如下:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}算法题
Leetcode 77. 组合
题目链接:77. 组合
大佬视频讲解:组合视频讲解
个人思路
组合问题就是不能使得结果重复,只能暴力解法,使用递归循环再加回溯来解决。
解法
先回顾一下组合和排列。组合是不强调元素顺序的,排列是强调元素顺序。
例如:{1, 2} 和 {2, 1} 在组合上,就是一个集合,因为不强调顺序,而要是排列的话,{1, 2} 和 {2, 1} 就是两个集合了。
记住组合无序,排列有序,就可以了。
回溯法
把组合问题抽象为如下树形结构
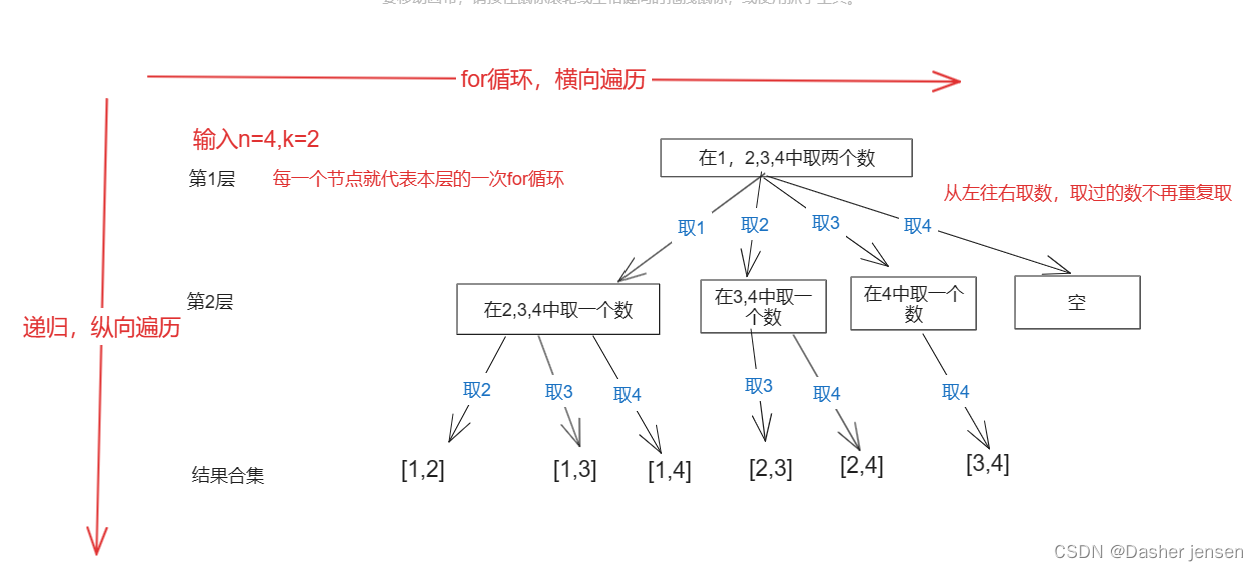
每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围。所以输入的n相当于树的宽度,k相当于树的深度。每次搜索到了叶子节点,就找到了一个结果。所以把达到叶子节点的结果收集起来,就可以求得 n个数中k个数的组合集合。
回溯法三部曲
1.递归函数的返回值以及参数
在这里要定义两个全局变量,一个用来存放符合条件单一结果,一个用来存放符合条件结果的集合。函数里一定有两个参数,既然是集合n里面取k个数,那么n和k是两个int型的参数。
然后还需要一个参数,为int型变量startIndex;startIndex用来记录下一层递归,搜索的起始位置,来防止出现重复的组合。
从下图中红线部分可以看出,在集合[1,2,3,4]取1之后,下一层递归,就要在[2,3,4]中取数了,那么下一层递归如何知道从[2,3,4]中取数呢,靠的就是startIndex。

2.回溯函数终止条件
到达叶子节点就找到一个结果,即path这个数组的大小如果达到k,说明找到了一个子集大小为k的组合了,在图中path存的就是根节点到叶子节点的路径。此时用result二维数组,把path保存起来,并终止本层递归。

3.单层搜索的过程
回溯法的搜索过程就是一个树型结构的遍历过程
在上图中,可以看出for循环用来横向遍历,递归的过程是纵向遍历。for循环每次从startIndex开始遍历,然后用path保存取到的节点i。而backtracking(递归函数)通过不断调用自己一直往深处遍历,总会遇到叶子节点,遇到了叶子节点就要返回。backtracking的下面部分就是回溯的操作了,撤销本次处理的结果。
class Solution {List<List<Integer>> result= new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combine(int n, int k) {backtracking(n,k,1);return result;}//startIndex 用来记录本层递归的中,集合从哪里开始遍历public void backtracking(int n,int k,int startIndex){if (path.size() == k){//终止条件result.add(new ArrayList<>(path));return;}for (int i =startIndex;i<=n;i++){//横向遍历path.add(i);//加入结果集backtracking(n,k,i+1);//递归:纵向遍历path.removeLast();//回溯}}
}时间复杂度:O(n * 2^n));(循环n个元素,2^n表示所有可能的子集数量)
空间复杂度:O(n);(递归栈的深度最多为 n)
上面代码和这个 模板基本一样,这就是后续做回溯法的模板代码了!
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}回溯剪枝优化
如何优化得画图来看。举一个例子,n = 4,k = 4的话,那么第一层for循环的时候,从元素2开始的遍历都没有意义了。 在第二层for循环,从元素3开始的遍历都没有意义了。
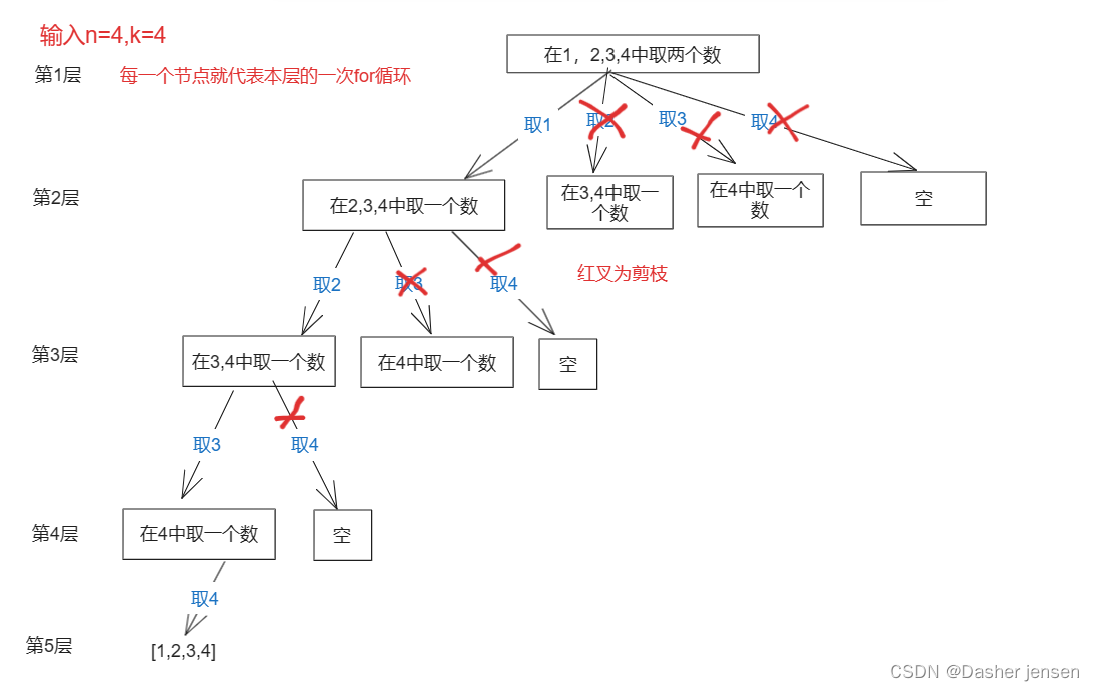
图中每一个节点,就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。所以,可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。如果for循环选择的起始位置之后的元素个数 已经不足 题目需要的元素个数了,那么就没有必要搜索了。
注意以下代码中的i,就是for循环里选择的起始位置。
接下来看一下优化过程如下:
已经选择的元素个数:path.size();
还需要的元素个数为: k - path.size();
在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
这样之所以需要+1,是因为包括起始位置,需要是一个左闭的集合。
举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。那么从2开始搜索都是合理的,可以是组合[2, 3, 4]。
class Solution {List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combine(int n, int k) {combineHelper(n, k, 1);return result;}//startIndex用来记录本层递归的中,集合从哪里开始遍历private void combineHelper(int n, int k, int startIndex){//终止条件if (path.size() == k){result.add(new ArrayList<>(path));return;}for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){path.add(i);//加入结果集combineHelper(n, k, i + 1);//递归path.removeLast();//回溯}}
}时间复杂度:O(n * 2^n));(循环n个元素,2^n表示所有可能的子集数量)
空间复杂度:O(n);(递归栈的深度最多为 n)
以上是个人的思考反思与总结,若只想根据系列题刷,参考卡哥的网址代码随想录算法官网
相关文章:

算法打卡day21|回溯法篇01|理论知识,Leetcode 77.组合
回溯法理论知识 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。所以回溯函数也就是递归函数,指的都是一个函数。 回溯法的效率 回溯法并不是什么高效的算法。因为回溯的本质是穷举,…...

C++ 输入输出
输入 1.1 cin >> str; 遇到“空格”、“TAB”、“回车”就停止 string str; cin >> str;1.2 getline(cin, str) 可用于输入一行数据,遇到空格不会停止,读入string字符中 便于读取一行一行的数据 while(getline(cin, str)){if(str "EN…...

FPGA高端项目:FPGA基于GS2971+GS2972架构的SDI视频收发+HLS图像缩放+多路视频拼接,提供4套工程源码和技术支持
目录 1、前言免责声明 2、相关方案推荐本博主所有FPGA工程项目-->汇总目录本博已有的 SDI 编解码方案本方案的SDI接收发送本方案的SDI接收图像缩放应用本方案的SDI接收纯verilog图像缩放纯verilog多路视频拼接应用本方案的SDI接收OSD动态字符叠加输出应用本方案的SDI接收HLS…...

【gpt实践】50个提升工作效率的GPT指令
收集整理了50个工作不同场景中可能会用到的gpt指令,希望对大家有帮助。 1. 用「532规则」定制月度宣传规划 提示:“对于我的 [产品/服务] 在 [社交媒体平台上 ]定位 [我的目标受众]”,使用 5-3-2 规则制定 1 个月的社交媒体内容计划。” Pro…...
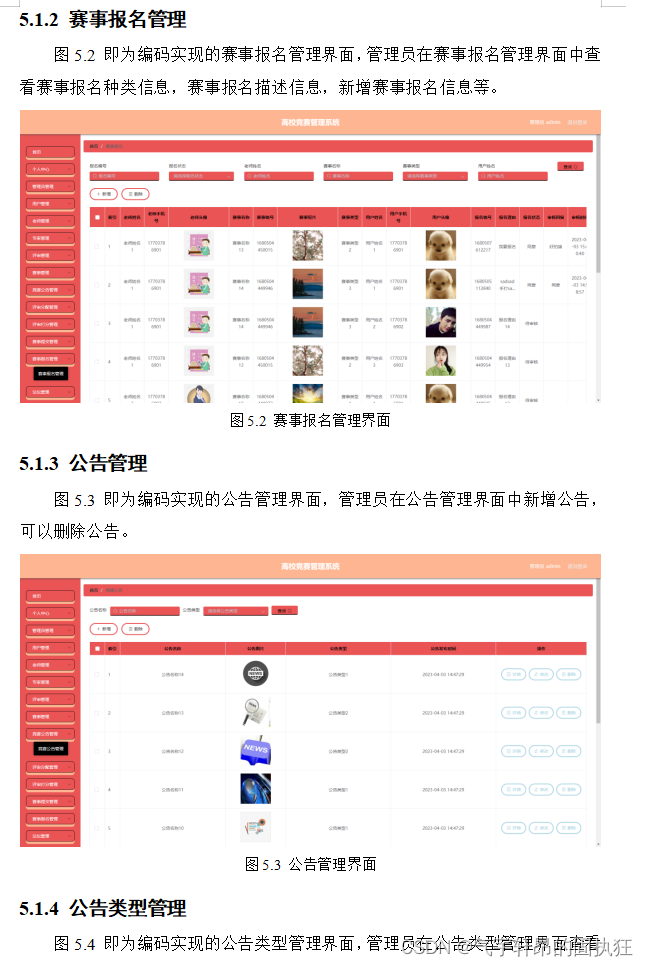
基于Springboot的高校竞赛管理系统(有报告)。Javaee项目,springboot项目。
演示视频: 基于Springboot的高校竞赛管理系统(有报告)。Javaee项目,springboot项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构…...
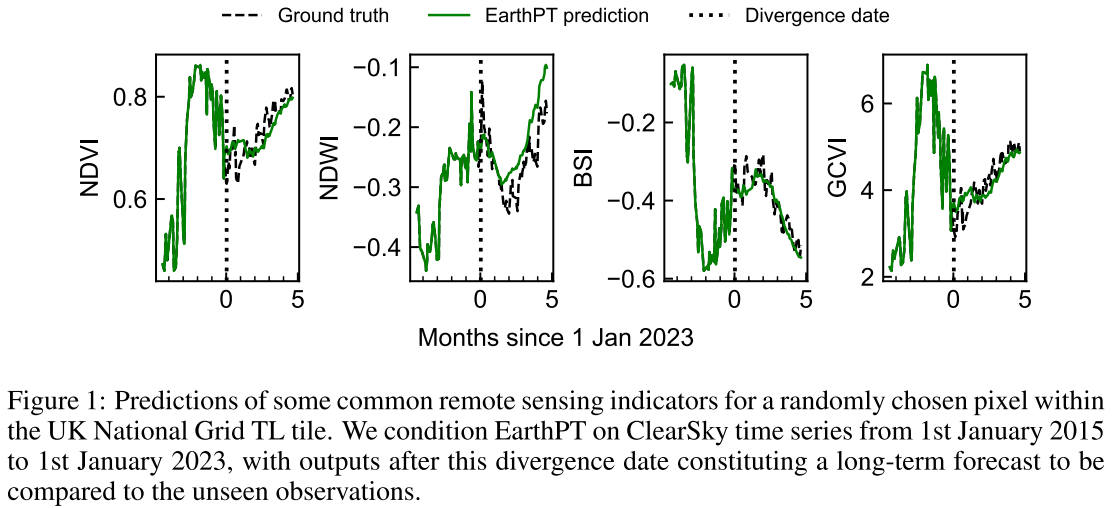
论文阅读——EarthPT
EarthPT: a time series foundation model for Earth Observation 一个Earth Observation (EO)预训练的Transformer。EarthPT是一个7亿参数解码Transformer基础模型,以自回归自监督方式进行训练,并专门针对EO用例进行开发。我们证明了EarthPT是一个有效的…...

软件测评中心:进行科技成果鉴定测试的注意事项和好处简析
软件产品科技成果鉴定是有效评价科技成果质量和水平的方法之一,也是鼓励科技成果通过市场竞争等方式得到有效的评价和认可,可以推动科技成果的进步和转化。 一、进行科技成果鉴定测试时的注意事项: 1、应由具备一定资质和能力的专业机构…...
Android 系统开发工具大全
写给应用开发的 Android Framework 教程——玩转AOSP篇之 Android 系统开发工具推荐 下面推荐的是我常用的工具,如果你有好用的开发工具欢迎在评论区留言讨论交流。 1. SSH 服务与 Tabby Terminal SSH 服务使得我们在其他平台上通过 SSH 客户端程序即可访问到我们…...
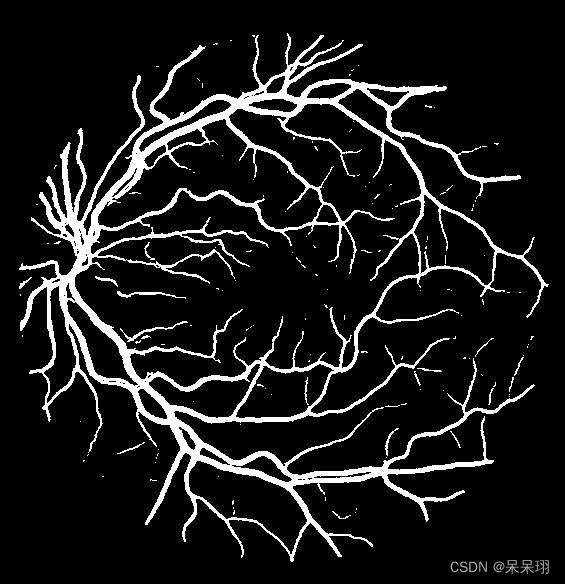
C版本的-Unet-rknn推理
1. 前言 之前就想着使用rknn的c版本的api做推理看看,找了一个简单的,那就unet吧,本来想着用rk的demo文件,但是里面是mobilenet,相关的函数没有,卡这也卡了好久,突然发现tengine相关的后处理&…...

Transformer的前世今生 day04(ELMO、Attention注意力机制)
ELMO 前情回顾 NNLM模型:主要任务是在预测下一个词,副产品是词向量Word2Vec模型:主要任务是生成词向量 CBOW:训练目标是根据上下文预测目标词Skip-gram:训练目标是根据目标词预测上下文词 ELMO模型的流程 针对Wor…...
稀碎从零算法笔记Day19-LeetCode:相交链表
题型:链表基本操作 链接:160. 相交链表 - 力扣(LeetCode) 来源:LeetCode 题目描述 给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点&…...
AI系统性学习03—ChatGPT开发教程
文章目录 1、OpenAI关键概念⭐️2、OpenAI SDK介绍3、OpenAI API KEY&API 认证3.1 REST API安全认证 4、OpenAI模型⭐️4.1 模型分类4.2 GPT44.3 GPT-3.54.4 Embeddings 5、OpenAI快速入门6、Function calling(函数调用)⭐️⭐️⭐️6.1 应用场景6.2 支持function calling的…...

每日一练 | 华为认证真题练习Day201
1、BGP Notification报文Error Code为2时表示open消息错误,其中包含如下哪些错误子码?(多选) A. 1-不支持的版本号 B. 2-错误的对等体AS号 C. 2-错误的对等体AS号 D. 4-错误的属性列表 2、A greate命令(aggregate ipy4-addre…...

nginx日志统计qps
1.QPS QPS全称为Queries Per Second,即每秒钟处理的请求数量。对于一个高并发应用来说,QPS是非常重要的性能指标,它反映了应用处理请求的能力。在实际应用中,QPS的大小取决于应用的负载和应用本身的性能。 QPS req/sec 请求数/…...
9.登入页面
登入页面 在pages中新建页面login 修改代码 <template><view></view> </template><script setup></script><style lang"scss"></style>添加头像组件 官网 https://vkuviewdoc.fsq.pub/components/avatar.html …...
)
js封装SDK 在VUE、小程序、公众号直接调用js调用后端接口(本文以vue项目为例)
1.封装一个js文件msgSdk.js 注意:需要修改这个请求地址 apiServiceAddress ;(function () {if (window.msgSdk) {return}var msgSdk (function () {var m_msgSdk thisvar apiServiceAddress"http://172.12.14.5:8000"this.I_SendHTTPRequest functi…...
ideaSSM社区二手交易平台C2C模式开发mysql数据库web结构java编程计算机网页源码maven项目
一、源码特点 idea ssm 社区二手交易平台系统是一套完善的完整信息管理系统,结合SSM框架完成本系统SpringMVC spring mybatis ,对理解JSP java编程开发语言有帮助系统采用SSM框架(MVC模式开发),系统具有完整的源代码…...
)
利用子类化技术拦截win32窗口各种消息(包括但不限于鼠标键盘消息)
创建子类化函数: 首先,您需要编写一个子类化函数,该函数将用于处理编辑框的消息。这个函数通常会拦截并处理您感兴趣的消息,比如鼠标消息。 子类化编辑框: 在窗口程序中找到编辑框的句柄(HWND)…...
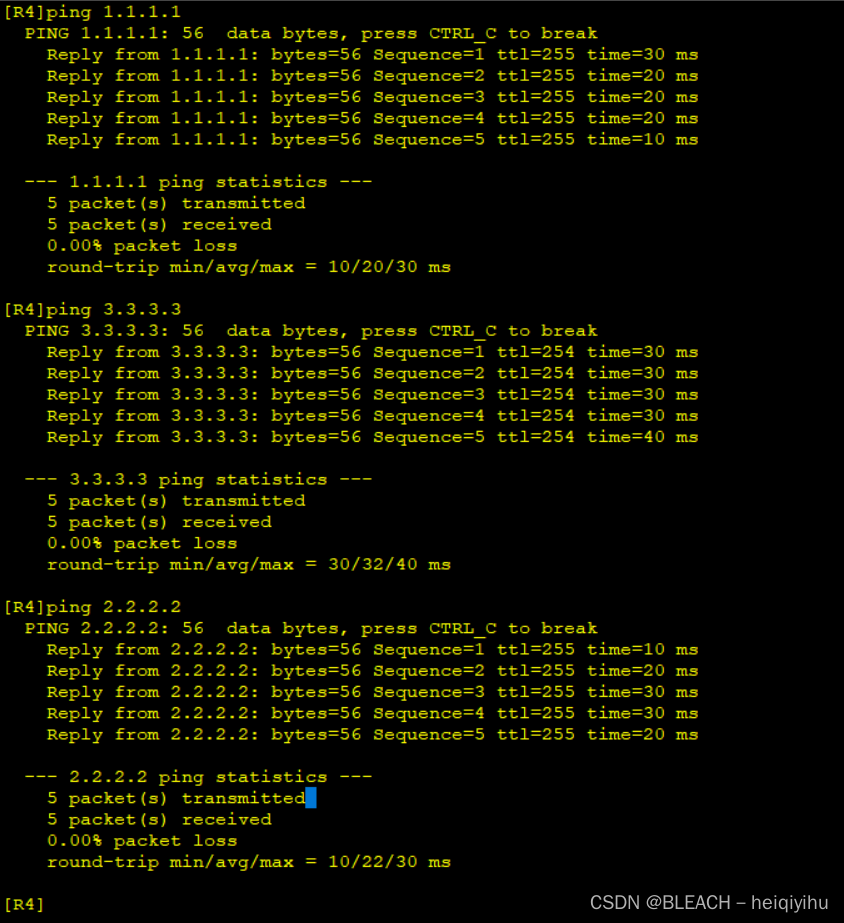
HCIP—OSPF课后练习一
本实验模拟了一个企业网络场景,R1、R2、R3为公司总部网络的路由器,R4、R5分别为企业分支机构1和分支机构2的路由器,并且都采用双上行方式与企业总部相连。整个网络都运行OSPF协议,R1、R2、R3之间的链路位于区域0,R4与R…...

Android 13.0 kenel和frameworks中修改ram运行内存的功能实现
1.前言 在13.0的系统rom产品开发定制中,在对一些产品开发中的配置需求方面,在产品后续订单中,产品提出要提高硬件配置,但是硬件方面已经定板,项目时间比较仓促,所以 来不及对硬件重新定制,就需要软件方面在ram运行内存的容量大小方面作假,修改ram真实的大小容量,所以…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
