Bert模型输出:last_hidden_state转换为pooler_output
1. BERT模型的输出
在BERT模型中,last_hidden_state和pooler_output是两个不同的输出。
(1) last_hidden_state:
last_hidden_state是指BERT模型中最后一个隐藏层的隐藏状态。它是一个三维张量,其形状为[batch_size, sequence_length, hidden_size]。其中,batch_size是输入序列的批量大小,sequence_length是输入序列的长度,hidden_size是BERT模型的隐藏层大小(通常为768)。
last_hidden_state保存了输入序列中每个token对应的隐藏状态,这些隐藏状态经过多层的Transformer编码器处理得到。在多数任务中,可以直接使用这个张量进行下游任务的训练或者特征提取。
(2) pooler_output:
pooler_output是指BERT模型中经过一个特殊的池化层后得到的句子级别表示。它是一个二维张量,其形状为[batch_size, hidden_size]。
pooler_output是通过对BERT模型最后一个隐藏层的第一个token([CLS] token)的隐藏状态应用一个全连接层得到的。这个全连接层的参数在预训练过程中被学习得到。pooler_output可以看作是整个输入序列的压缩表示,通常用于句子级别的任务,如文本分类。
总的来说,last_hidden_state提供了序列中每个token的隐藏状态信息,而pooler_output提供了整个句子的语义表示。
2. last_hidden_state转换为pooler_output
在BERT模型中,last_hidden_state是最后一个隐藏层的隐藏状态,而pooler_output是通过应用一个全连接层(通常是一个线性变换加上激活函数)到last_hidden_state中的特殊token([CLS] token)得到的。
首先从last_hidden_state中提取出每个样本的第一个token(即[CLS] token)的隐藏状态。然后,我们定义了一个线性层pooler_layer,将隐藏状态映射到与BERT模型的隐藏大小相同的空间。最后,我们应用了tanh激活函数,得到 pooler_output,这是整个句子的语义表示。这个pooler_output可以用于句子级别的任务,例如文本分类。
请确保poor_layer的权重是正确初始化的。通常情况下,应该使用预训练的BERT模型的权重来初始化它。可以在实例化poor_layer时进行这样的初始化。如果使用的是transformers库,它提供了加载预训练BERT模型并提取pooler_output的方法。要使用预训练的BERT模型的权重来初始化线性层 pooler_layer,可以从预训练的BERT模型中加载权重,并将这些权重用作 pooler_layer的初始权重。通常情况下,会使用Hugging Face的 transformers库来加载预训练的BERT模型。
以下是一个示例代码,演示如何使用transformers库来加载预训练的BERT模型,并使用其中的权重来初始化 pooler_layer:
from transformers import BertModel, BertTokenizer#加载预训练的Bert模型和tokenizer
tokenizer = BertTokenizer.from_pretrained('bert-base-uncased')
extractor = BertModel.from_pretrained('bert-base-uncased')#text是原始文本数据
x = tokenizer(text, padding=True, truncation=True, max_length=256, return_tensors="pt").to(device)x = extractor(**x)#获取hidden_state
x1= x['last_hidden_state']# 定义一个线性层,将最后一个隐藏层的第一个token的隐藏状态映射到pooler_output
pooler_layer = nn.Linear(768, 768).to(device)# 使用BERT模型的权重来初始化pooler_layer的权重
with torch.no_grad():pooler_layer.weight.copy_(extractor.pooler.dense.weight)pooler_layer.bias.copy_(extractor.pooler.dense.bias)# 获取CLS token的隐藏状态(最后隐藏层的第一个token),取出每个样本的第一个token的隐藏状态
cls_token_state = x1[:, 0, :].to(device)## 应用线性层并使用激活函数
x1 = torch.tanh(pooler_layer(cls_token_state)).to(device)#直接获取pooler_output
x2=x['pooler_output'].to(device)在这个示例中,我们首先从预训练的BERT模型中加载了tokenizer和BERT模型。然后,我们创建了一个与BERT模型隐藏大小相同的线性层 pooler_layer。最后,我们使用`bert_model.pooler.dense`中的权重来初始化`pooler_layer`的权重。这样,`pooler_layer`就被正确初始化了,并可以用于将`last_hidden_state`变换为`pooler_output`。最后x1和x2的结果相同。
相关文章:

Bert模型输出:last_hidden_state转换为pooler_output
1. BERT模型的输出 在BERT模型中,last_hidden_state和pooler_output是两个不同的输出。 (1) last_hidden_state: last_hidden_state是指BERT模型中最后一个隐藏层的隐藏状态。它是一个三维张量,其形状为[batch_size, sequence_length, hidden_size]。其…...

Docker Compose 基本语法
services 是顶级节点,也就是你要启动的服务全部放在这里。 MySOL就是我们预期中的一个服务。 mysql8:指的是我们这个服务叫 mysql8. image:我们这个服务里运行的是什么镜像,或者说跑的是什么。这里指定了使用 mysql:8.0.29 这个版本。 command:启动命令&…...

【算法集训】基础算法:贪心
1913. 两个数对之间的最大乘积差 void insertSort(int * a, int n) {for(int i 1; i < n; i) {int temp a[i];int j i - 1;while(j > 0 && temp < a[j]) {a[j 1] a[j];j--;}a[j 1] temp;} }int maxProductDifference(int* nums, int numsSize){insert…...
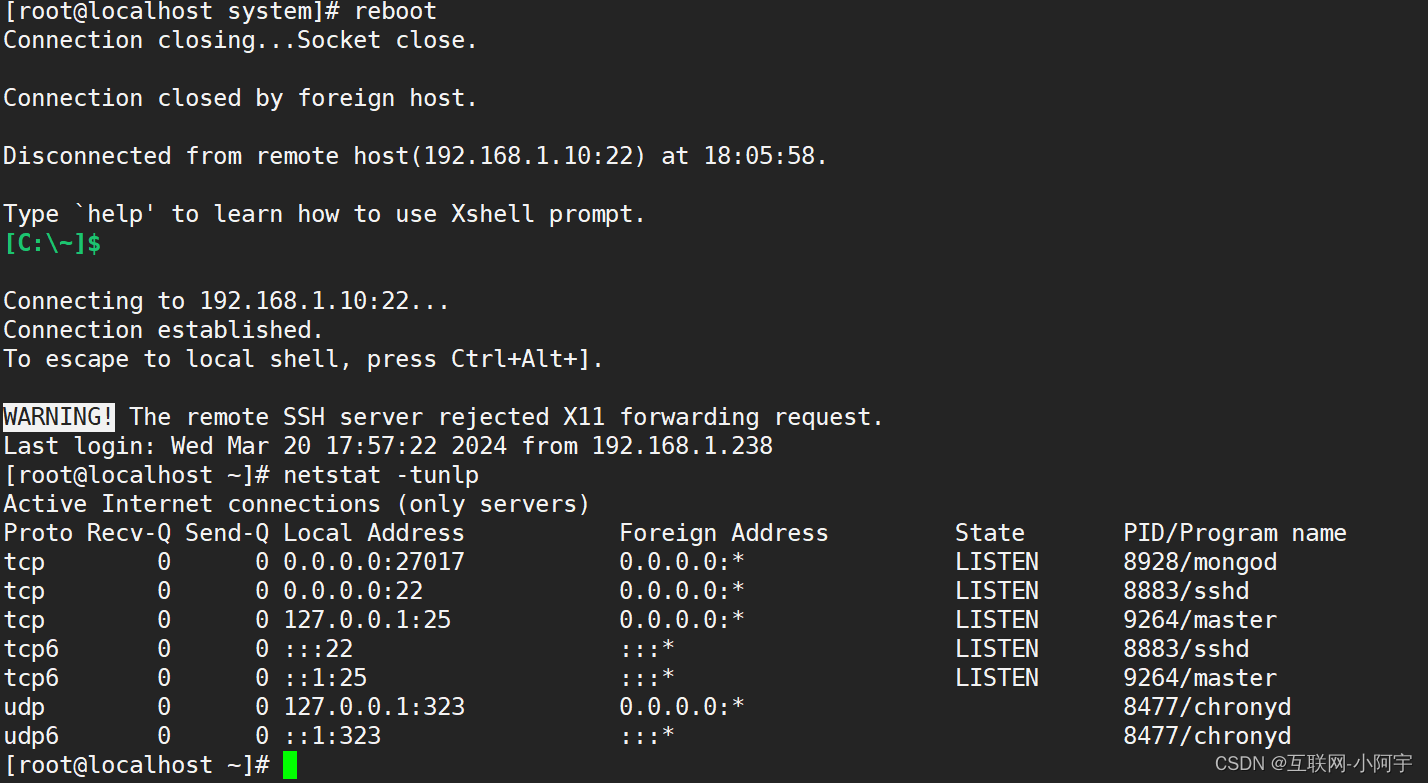
Centos7部署单节点MongoDB(V4.2.25)
🎈 作者:互联网-小啊宇 🎈 简介: CSDN 运维领域创作者、阿里云专家博主。目前从事 Kubernetes运维相关工作,擅长Linux系统运维、开源监控软件维护、Kubernetes容器技术、CI/CD持续集成、自动化运维、开源软件部署维护…...
)
隐私计算笔记(1)
一、可信流通体系 建立数据来源可确认、使用范围可界定、流通过程可追溯、安全风险可防范的数据可流通体系。 二、产生信任的基石 身份可确认利益可依赖能力有预期行为有后果 三、数据流通不可信风险 内循环:在内部循环中,数据持有方在其自身的运维…...

查询方法需要使用事务吗?
当数据库隔离级别是默认的可重复读(Repeatable Read)时,如果查询语句只有一条则不需要事务. 当有多条查询sql语句且需要确保多条sql语句处于同一时间维度时则需要使用事务来确保多条SQL语句处于同一时间节点. 相关知识点 mysql查询当前事务隔…...

剑指offer面试题40 数组中只出现一次的数字
考察点 异或运算,与运算知识点 题目 分析 本题目要求数组中只出现一次的俩个数字,并且要求O(1)时间复杂度和空间复杂度。试想一下如果只有一个数字出现一次,那么针对全部元素做异或运算就可以了,因为相同元素异或为0。现在有俩…...
gitLab server version 13.12.1 is not supported
拉代码的时候,报的这个错,实际上就是因为gitLab 版本太低了,这里不准备升级版本,打算继续使用账号密码来拉取代码 在idea已经安装的插件中,去掉gitlab插件,如下: 之后再拉取代码,就…...

如何在 iPhone 上使用蓝牙鼠标
iPhone 不支持使用传统的鼠标指针。 然而,有一个名为“AssistiveTouch”的功能可以在屏幕上模拟类似光标的指针。 启用它的方法如下: 打开 iPhone 上的“设置”应用程序。转到“辅助功能”。向下滚动并选择“触摸”。点击“辅助触控”。切换开关以打开 …...
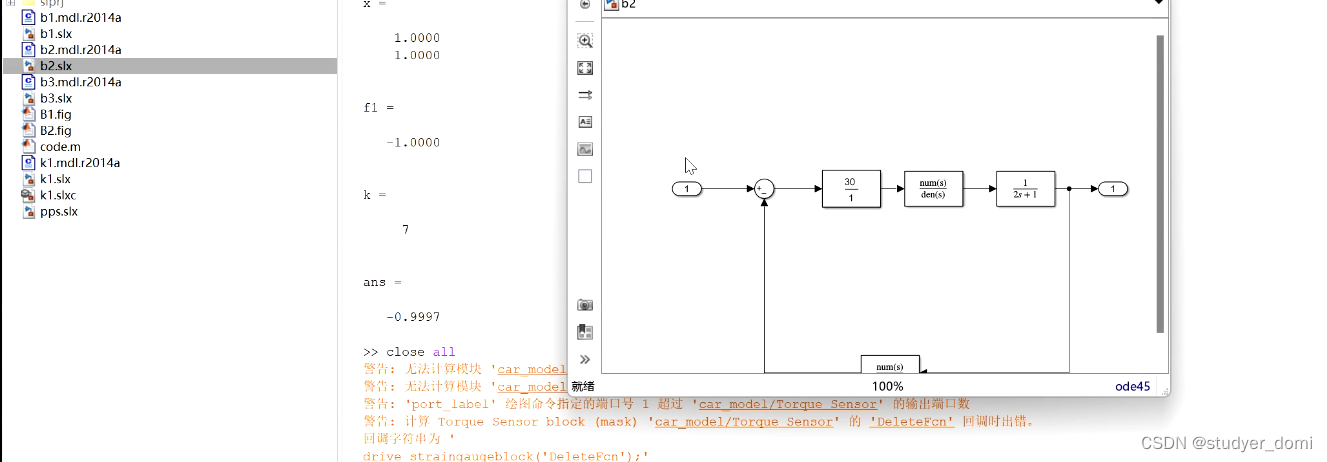
matlab simulink 电力系统同步发电机励磁系统的建模与仿真
1、内容简介 略 77-可以交流、咨询、答疑 电力系统同步发电机励磁系统的建模与仿真 建立MATLAB的同步发电机励磁调节系统仿真模型,最后建立了以PID和PSS为励磁控制方式的同步发电机励磁调节系统数学模型,在Simulink环境下进行了仿真,收到…...

AI新工具(20240320) AI创作一首属于自己的音乐; 轻松制作具有透明背景的高质量图像
✨ 1: Suno AI创作一首属于自己的音乐 Suno是一个革命性的人工智能平台,专注于音乐创作。在通俗的语言中,Suno允许用户仅通过提供歌词,自动为其创作旋律和演唱,产生完整的音乐作品。使用Suno的过程简单直观,不需要用…...

IT服务ITIL4 认证:助力企业数字化转型的必杀技!
随着科技的不断展和企业竞争的加剧,如何实现数字化转型成为了当今企业面临的重要课题。而学习ITIL4认证,尤其是ITIL4中级,将为企业的数字化转型提供有力的支持和帮助。 ITIL4认证 ITIL(Information Technology Infrastructure Li…...

微软聘请了谷歌DeepMind的联合创始人
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
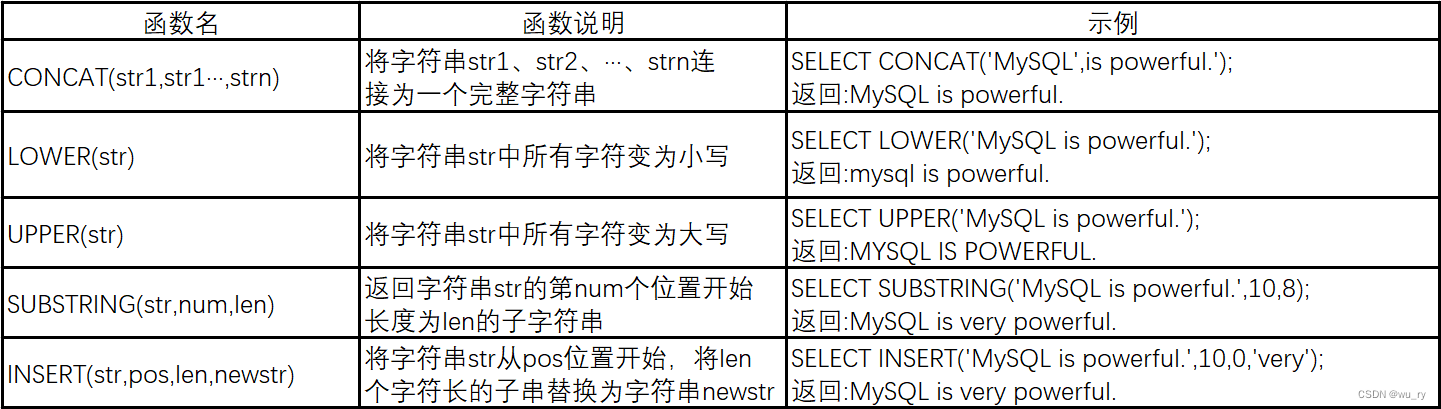
JavaMySQL高级一(下)
目录 1.常用函数 1.字符串函数 2.时间日期函数 3.聚合函数 4.数学函数 2.分布查询 3.子查询基础 1.简单子查询 1.常用函数 在程序开发过程中,除了简单的数据查询,还有基于已数据进行数据的统计分析计算等需求。因此,在SQL中将一…...
HCIA复习
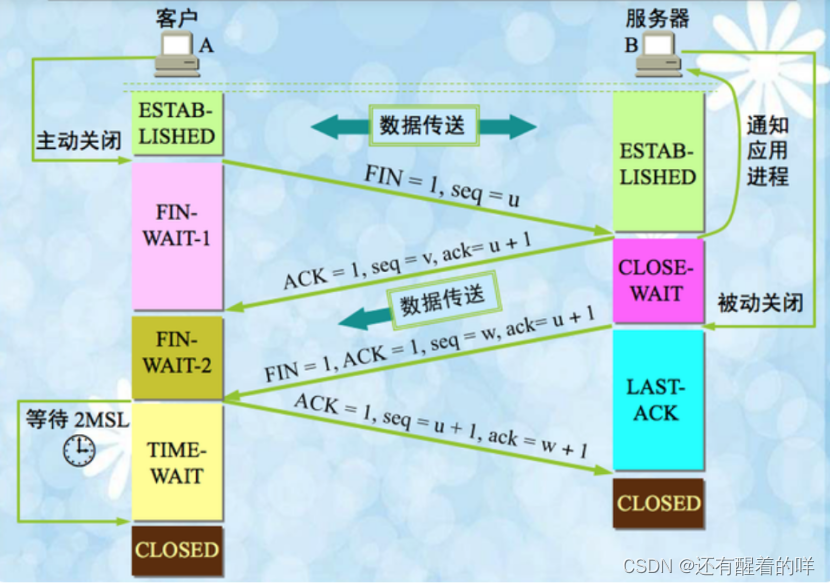
上面的文件里有思维导图哦~ 一、情景再现:ISP网络为学校提供了DNS服务,所以,DNS服务器驻留在ISP网络内,而不再学校网络内。DHCP服务器运行在学校网络的路由器上。 小明拿了一台电脑,通过网线,接入到校园网…...
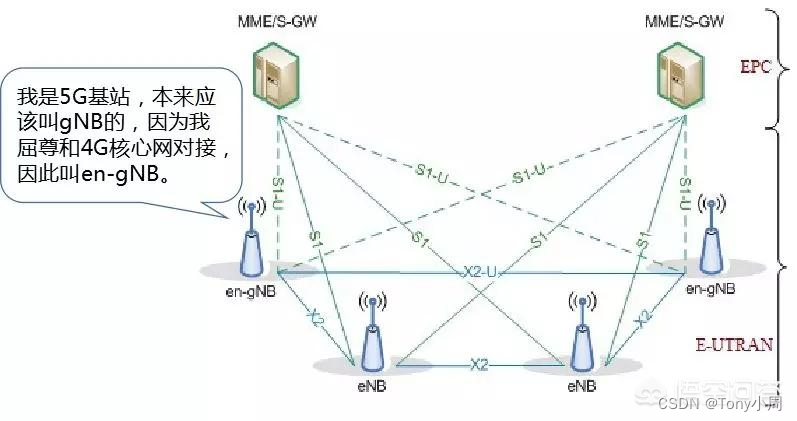
5G里面NR,gNB,en-gNB,ng-eNB是什么意思
不得不提一个国际组织,叫国际电信联盟(ITU, International Telecommunication Union),简称国际电联。我们先看看国际电联的自我介绍: 国际电信联盟 『国际电联 (国际电信联盟) 是主管信息通信技术事务(ICT)的联合国机…...

android 网络检测简单方法
如果连接的WiFi没有网络,无法通过简单的网络状态检查来判断其可用性。在这种情况下,你可以尝试使用以下方法来检测当前连接的WiFi是否可用: Ping测试:尝试通过向一个已知的可靠服务器发送Ping请求来检测连接的WiFi是否可用。如果…...
篇(二))
列表(list)篇(二)
文章目录 2.10 insert()函数2.11 list()函数2.12 pop() 函数2.13 remove()函数2.14 reverse()函数2.15 sort()函数2.16 sorted()函数2.17 sum()函数 2.10 insert()函数 在Python中,list.insert()是一个列表方法,用于在指定索引位置插入一个元素。这个方…...

Python的反射机制
本篇文章讨论Python中非常有趣且强大的概念——反射(Reflection)。想象一下,你正在编写一段代码,并希望这段代码能够具备自我认知和动态调整的能力。就好比一面镜子,能反映出它自身的属性和行为。在编程领域࿰…...
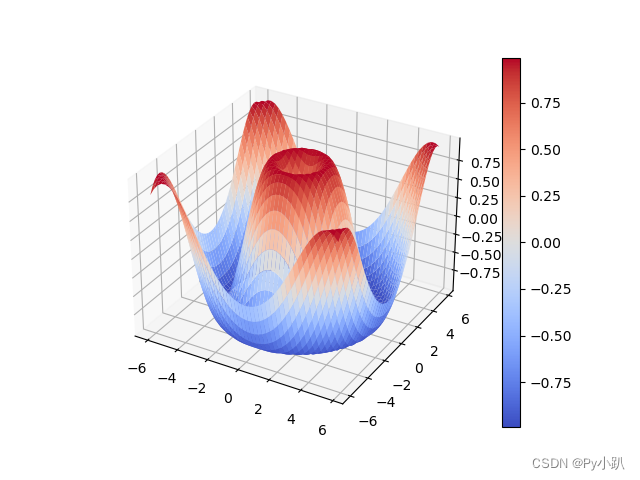
Python数学建模-2.9Matplotlib库
Matplotlib库是Python中一个非常流行的绘图库,它提供了大量的绘图工具,可以生成各种类型的静态、动态、交互式的图表。Matplotlib的设计初衷是为了与NumPy配合使用,从而提供一个强大的数学绘图工具。 1.Matplotlib的主要特点 丰富的图表类型…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...
