C语言经典算法-6
文章目录
- 其他经典例题跳转链接
- 31.数字拆解
- 32.得分排行
- 33.选择、插入、气泡排序
- 34.Shell 排序法 - 改良的插入排序
- 35.Shaker 排序法 - 改良的气泡排序
其他经典例题跳转链接
C语言经典算法-1
1.汉若塔 2. 费式数列 3. 巴斯卡三角形 4. 三色棋 5. 老鼠走迷官(一)6. 老鼠走迷官(二)7. 骑士走棋盘8. 八皇后9. 八枚银币10. 生命游戏
C语言经典算法-2
字串核对、双色、三色河内塔、背包问题(Knapsack Problem)、蒙地卡罗法求 PI、Eratosthenes筛选求质数
C语言经典算法-3
超长整数运算(大数运算)、长 PI、最大公因数、最小公倍数、因式分解、完美数、阿姆斯壮数
C语言经典算法-4
最大访客数、中序式转后序式(前序式)、后序式的运算、洗扑克牌(乱数排列)、Craps赌博游戏
C语言经典算法-5
约瑟夫问题(Josephus Problem)、排列组合、格雷码(Gray Code)、产生可能的集合、m元素集合的n个元素子集
C语言经典算法-6
数字拆解、得分排行,选择、插入、气泡排序、Shell 排序法 - 改良的插入排序、Shaker 排序法 - 改良的气泡排序
C语言经典算法-7
排序法 - 改良的选择排序、快速排序法(一)、快速排序法(二)、快速排序法(三)、合并排序法
C语言经典算法-8
基数排序法、循序搜寻法(使用卫兵)、二分搜寻法(搜寻原则的代表)、插补搜寻法、费氏搜寻法
C语言经典算法-9
稀疏矩阵、多维矩阵转一维矩阵、上三角、下三角、对称矩阵、奇数魔方阵、4N 魔方阵、2(2N+1) 魔方阵
31.数字拆解
说明
这个题目来自于 数字拆解,我将之改为C语言的版本,并加上说明。
题目是这样的:
3 = 2+1 = 1+1+1 所以3有三种拆法
4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1 共五种
5 = 4 + 1 = 3 + 2 = 3 + 1 + 1 = 2 + 2 + 1 = 2 + 1 + 1 + 1 = 1 + 1 +1 +1 +1
共七种
依此类推,请问一个指定数字NUM的拆解方法个数有多少个?
解法
我们以上例中最后一个数字5的拆解为例,假设f( n )为数字n的可拆解方式个数,而f(x, y)为使用y以下的数字来拆解x的方法个数,则观察:
5 = 4 + 1 = 3 + 2 = 3 + 1 + 1 = 2 + 2 + 1 = 2 + 1 + 1 + 1 = 1 + 1 +1 +1 +1
使用函式来表示的话:
f(5) = f(4, 1) + f(3,2) + f(2,3) + f(1,4) + f(0,5)
其中f(1, 4) = f(1, 3) + f(1, 2) + f(1, 1),但是使用大于1的数字来拆解1没有意义,所以f(1, 4) = f(1, 1),而同样的,f(0, 5)会等于f(0, 0),所以:
f(5) = f(4, 1) + f(3,2) + f(2,3) + f(1,1) + f(0,0)
依照以上的说明,使用动态程式规画(Dynamic programming)来进行求解,其中f(4,1)其实就是f(5-1, min(5-1,1)),f(x, y)就等于f(n-y, min(n-x, y)),其中n为要拆解的数字,而min()表示取两者中较小的数。
使用一个二维阵列表格table[x][y]来表示f(x, y),刚开始时,将每列的索引0与索引1元素值设定为1,因为任何数以0以下的数拆解必只有1种,而任何数以1以下的数拆解也必只有1种:
for(i = 0; i < NUM +1; i++){ table[i][0] = 1; // 任何数以0以下的数拆解必只有1种 table[i][1] = 1; // 任何数以1以下的数拆解必只有1种
}
接下来就开始一个一个进行拆解了,如果数字为NUM,则我们的阵列维度大小必须为NUM x (NUM/2+1),以数字10为例,其维度为10 x 6我们的表格将会如下所示:
1 1 0 0 0 0
1 1 0 0 0 0
1 1 2 0 0 0
1 1 2 3 0 0
1 1 3 4 5 0
1 1 3 5 6 7
1 1 4 7 9 0
1 1 4 8 0 0
1 1 5 0 0 0
1 1 0 0 0 0
实作
C
#include <stdio.h>
#include <stdlib.h>
#define NUM 10 // 要拆解的数字
#define DEBUG 0 int main(void) { int table[NUM][NUM/2+1] = {0}; // 动态规画表格 int count = 0; int result = 0; int i, j, k; printf("数字拆解\n"); printf("3 = 2+1 = 1+1+1 所以3有三种拆法\n"); printf("4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1"); printf("共五种\n"); printf("5 = 4 + 1 = 3 + 2 = 3 + 1 + 1");printf(" = 2 + 2 + 1 = 2 + 1 + 1 + 1 = 1 + 1 +1 +1 +1");printf("共七种\n"); printf("依此类推,求 %d 有几种拆法?", NUM); // 初始化 for(i = 0; i < NUM; i++){ table[i][0] = 1; // 任何数以0以下的数拆解必只有1种 table[i][1] = 1; // 任何数以1以下的数拆解必只有1种 } // 动态规划 for(i = 2; i <= NUM; i++){ for(j = 2; j <= i; j++){ if(i + j > NUM) // 大于 NUM continue; count = 0; for(k = 1 ; k <= j; k++){ count += table[i-k][(i-k >= k) ? k : i-k]; } table[i][j] = count; } } // 计算并显示结果 for(k = 1 ; k <= NUM; k++) result += table[NUM-k][(NUM-k >= k) ? k : NUM-k]; printf("\n\nresult: %d\n", result); if(DEBUG) { printf("\n除错资讯\n"); for(i = 0; i < NUM; i++) { for(j = 0; j < NUM/2+1; j++) printf("%2d", table[i][j]); printf("\n"); } } return 0;
}
32.得分排行
说明假设有一教师依学生座号输入考试分数,现希望在输入完毕后自动显示学生分数的排行,当然学生的分数可能相同。
解法这个问题基本上要解不难,只要使用额外的一个排行阵列走访分数阵列就可以了,直接使用下面的程式片段作说明:
for(i = 0; i < count; i++) { juni[i] = 1; for(j = 0; j < count; j++) { if(score[j] > score[i]) juni[i]++; }
}
printf("得分\t排行\n");
for(i = 0; i < count; i++) printf("%d\t%d\n", score[i], juni[i]);
上面这个方法虽然简单,但是反覆计算的次数是n^2,如果n值变大,那么运算的时间就会拖长;改变juni阵列的长度为n+2,并将初始值设定为0,如下所示:

接下来走访分数阵列,并在分数所对应的排行阵列索引元素上加1,如下所示:

将排行阵列最右边的元素设定为1,然后依序将右边的元素值加至左边一个元素,最后排行阵列中的「分数+1」」就是得该分数的排行,如下所示:
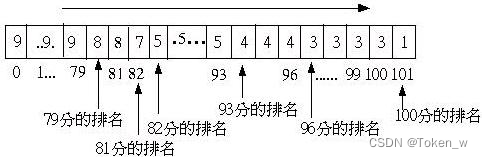
这样的方式看起来复杂,其实不过在计算某分数之前排行的人数,假设89分之前的排行人数为x人,则89分自然就是x+1了,这也是为什么排行阵列最右边要设定为1的原因;如果89分有y人,则88分自然就是x+y+1,整个阵列右边元素向左加的原因正是如此。
如果分数有负分的情况,由于C/C++或Java等程式语言无法处理负的索引,所以必须加上一个偏移值,将所有的分数先往右偏移一个范围即可,最后显示的时候记得减回偏移值就可以了。
#include <stdio.h>
#include <stdlib.h>
#define MAX 100
#define MIN 0 int main(void) { int score[MAX+1] = {0}; int juni[MAX+2] = {0}; int count = 0, i; do { printf("输入分数,-1结束:"); scanf("%d", &score[count++]); } while(score[count-1] != -1);count--; for(i = 0; i < count; i++) juni[score[i]]++; juni[MAX+1] = 1; for(i = MAX; i >= MIN; i--) juni[i] = juni[i] + juni[i+1]; printf("得分\t排行\n"); for(i = 0; i < count; i++) printf("%d\t%d\n", score[i], juni[score[i]+1]); return 0;
}
33.选择、插入、气泡排序
说明选择排序(Selection sort)、插入排序(Insertion sort)与气泡排序(Bubble sort)这三个排序方式是初学排序所必须知道的三个基本排序方式,它们由于速度不快而不实用(平均与最快的时间复杂度都是O(n2)),然而它们排序的方式确是值得观察与探讨的。
解法
选择排序
将要排序的对象分作两部份,一个是已排序的,一个是未排序的,从后端未排序部份选择一个最小值,并放入前端已排序部份的最后一个,例如:
排序前:70 80 31 37 10 1 48 60 33 80
[1] 80 31 37 10 70 48 60 33 80 选出最小值1
[1 10] 31 37 80 70 48 60 33 80 选出最小值10
[1 10 31] 37 80 70 48 60 33 80 选出最小值31
[1 10 31 33] 80 70 48 60 37 80 …
[1 10 31 33 37] 70 48 60 80 80 …
[1 10 31 33 37 48] 70 60 80 80 …
[1 10 31 33 37 48 60] 70 80 80 …
[1 10 31 33 37 48 60 70] 80 80 …
[1 10 31 33 37 48 60 70 80] 80 …
插入排序
像是玩朴克一样,我们将牌分作两堆,每次从后面一堆的牌抽出最前端的牌,然后插入前面一堆牌的适当位置,例如:
排序前:92 77 67 8 6 84 55 85 43 67
[77 92] 67 8 6 84 55 85 43 67 将77插入92前
[67 77 92] 8 6 84 55 85 43 67 将67插入77前
[8 67 77 92] 6 84 55 85 43 67 将8插入67前
[6 8 67 77 92] 84 55 85 43 67 将6插入8前
[6 8 67 77 84 92] 55 85 43 67 将84插入92前
[6 8 55 67 77 84 92] 85 43 67 将55插入67前
[6 8 55 67 77 84 85 92] 43 67 …
[6 8 43 55 67 77 84 85 92] 67 …
[6 8 43 55 67 67 77 84 85 92] …
气泡排序法
顾名思义,就是排序时,最大的元素会如同气泡一样移至右端,其利用比较相邻元素的方法,将大的元素交换至右端,所以大的元素会不断的往右移动,直到适当的位置为止。
基本的气泡排序法可以利用旗标的方式稍微减少一些比较的时间,当寻访完阵列后都没有发生任何的交换动作,表示排序已经完成,而无需再进行之后的回圈比较与交换动作,例如:
排序前:95 27 90 49 80 58 6 9 18 50
27 90 49 80 58 6 9 18 50 [95] 95浮出
27 49 80 58 6 9 18 50 [90 95] 90浮出
27 49 58 6 9 18 50 [80 90 95] 80浮出
27 49 6 9 18 50 [58 80 90 95] …
27 6 9 18 49 [50 58 80 90 95] …
6 9 18 27 [49 50 58 80 90 95] …
6 9 18 [27 49 50 58 80 90 95] 由于接下来不会再发生交换动作,排序提早结束
在上面的例子当中,还加入了一个观念,就是当进行至i与i+1时没有交换的动作,表示接下来的i+2至n已经排序完毕,这也增进了气泡排序的效率。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {int t; t = x; x = y; y = t;} void selsort(int[]); // 选择排序
void insort(int[]); // 插入排序
void bubsort(int[]); // 气泡排序 int main(void) { int number[MAX] = {0}; int i; srand(time(NULL)); printf("排序前:"); for(i = 0; i < MAX; i++) { number[i] = rand() % 100; printf("%d ", number[i]); } printf("\n请选择排序方式:\n"); printf("(1)选择排序\n(2)插入排序\n(3)气泡排序\n:"); scanf("%d", &i); switch(i) { case 1: selsort(number); break; case 2: insort(number); break; case 3: bubsort(number); break; default: printf("选项错误(1..3)\n"); } return 0;
} void selsort(int number[]) { int i, j, k, m; for(i = 0; i < MAX-1; i++) { m = i; for(j = i+1; j < MAX; j++) if(number[j] < number[m]) m = j; if( i != m) SWAP(number[i], number[m]) printf("第 %d 次排序:", i+1); for(k = 0; k < MAX; k++) printf("%d ", number[k]); printf("\n"); } } void insort(int number[]) { int i, j, k, tmp; for(j = 1; j < MAX; j++) { tmp = number[j]; i = j - 1; while(tmp < number[i]) { number[i+1] = number[i]; i--; if(i == -1) break; } number[i+1] = tmp; printf("第 %d 次排序:", j); for(k = 0; k < MAX; k++) printf("%d ", number[k]); printf("\n"); }
} void bubsort(int number[]) { int i, j, k, flag = 1; for(i = 0; i < MAX-1 && flag == 1; i++) { flag = 0; for(j = 0; j < MAX-i-1; j++) { if(number[j+1] < number[j]) { SWAP(number[j+1], number[j]); flag = 1; } } printf("第 %d 次排序:", i+1); for(k = 0; k < MAX; k++) printf("%d ", number[k]); printf("\n"); }
}
34.Shell 排序法 - 改良的插入排序
说明
插入排序法由未排序的后半部前端取出一个值,插入已排序前半部的适当位置,概念简单但速度不快。
排序要加快的基本原则之一,是让后一次的排序进行时,尽量利用前一次排序后的结果,以加快排序的速度,Shell排序法即是基于此一概念来改良插入排序法。
解法
Shell排序法最初是D.L Shell于1959所提出,假设要排序的元素有n个,则每次进行插入排序时并不是所有的元素同时进行时,而是取一段间隔。
Shell首先将间隔设定为n/2,然后跳跃进行插入排序,再来将间隔n/4,跳跃进行排序动作,再来间隔设定为n/8、n/16,直到间隔为1之后的最 后一次排序终止,由于上一次的排序动作都会将固定间隔内的元素排序好,所以当间隔越来越小时,某些元素位于正确位置的机率越高,因此最后几次的排序动作将 可以大幅减低。
举个例子来说,假设有一未排序的数字如右:89 12 65 97 61 81 27 2 61 98
数字的总数共有10个,所以第一次我们将间隔设定为10 / 2 = 5,此时我们对间隔为5的数字进行排序,如下所示:
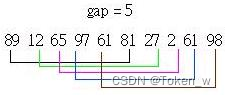
画线连结的部份表示 要一起进行排序的部份,再来将间隔设定为5 / 2的商,也就是2,则第二次的插入排序对象如下所示:

再来间隔设定为2 / 2 = 1,此时就是单纯的插入排序了,由于大部份的元素都已大致排序过了,所以最后一次的插入排序几乎没作什么排序动作了:

将间隔设定为n / 2是D.L Shell最初所提出,在教科书中使用这个间隔比较好说明,然而Shell排序法的关键在于间隔的选定,例如Sedgewick证明选用以下的间隔可以加 快Shell排序法的速度:
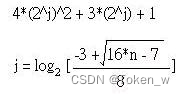
其中4*(2j)2 + 3*(2j) + 1不可超过元素总数n值,使用上式找出j后代入4*(2j)2 + 3*(2j) + 1求得第一个间隔,然后将2j除以2代入求得第二个间隔,再来依此类推。
后来还有人证明有其它的间隔选定法可以将Shell排序法的速度再加快;另外Shell排序法的概念也可以用来改良气泡排序法。
实作
C
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {int t; t = x; x = y; y = t;} void shellsort(int[]); int main(void) { int number[MAX] = {0}; int i; srand(time(NULL)); printf("排序前:"); for(i = 0; i < MAX; i++) { number[i] = rand() % 100; printf("%d ", number[i]); } shellsort(number); return 0;
} void shellsort(int number[]) { int i, j, k, gap, t; gap = MAX / 2; while(gap > 0) { for(k = 0; k < gap; k++) { for(i = k+gap; i < MAX; i+=gap) { for(j = i - gap; j >= k; j-=gap) { if(number[j] > number[j+gap]) { SWAP(number[j], number[j+gap]); } else break; } } } printf("\ngap = %d:", gap); for(i = 0; i < MAX; i++) printf("%d ", number[i]); printf("\n"); gap /= 2; }
}
35.Shaker 排序法 - 改良的气泡排序
说明
请看看之前介绍过的气泡排序法:
for(i = 0; i < MAX-1 && flag == 1; i++) { flag = 0; for(j = 0; j < MAX-i-1; j++) { if(number[j+1] < number[j]) { SWAP(number[j+1], number[j]); flag = 1; } }
}
事实上这个气泡排序法已经不是单纯的气泡排序了,它使用了旗标与右端左移两个方法来改进排序的效能,而Shaker排序法使用到后面这个观念进一步改良气泡排序法。
解法
在上面的气泡排序法中,交换的动作并不会一直进行至阵列的最后一个,而是会进行至MAX-i-1,所以排序的过程中,阵列右方排序好的元素会一直增加,使得左边排序的次数逐渐减少,如我们的例子所示:
排序前:95 27 90 49 80 58 6 9 18 50
27 90 49 80 58 6 9 18 50 [95] 95浮出
27 49 80 58 6 9 18 50 [90 95] 90浮出
27 49 58 6 9 18 50 [80 90 95] 80浮出
27 49 6 9 18 50 [58 80 90 95] …
27 6 9 18 49 [50 58 80 90 95] …
6 9 18 27 [49 50 58 80 90 95] …
6 9 18 [27 49 50 58 80 90 95]
方括号括住的部份表示已排序完毕,Shaker排序使用了这个概念,如果让左边的元素也具有这样的性质,让左右两边的元素都能先排序完成,如此未排序的元素会集中在中间,由于左右两边同时排序,中间未排序的部份将会很快的减少。
方法就在于气泡排序的双向进行,先让气泡排序由左向右进行,再来让气泡排序由右往左进行,如此完成一次排序的动作,而您必须使用left与right两个旗标来记录左右两端已排序的元素位置。
一个排序的例子如下所示:
排序前:45 19 77 81 13 28 18 19 77 11
往右排序:19 45 77 13 28 18 19 77 11 [81]
向左排序:[11] 19 45 77 13 28 18 19 77 [81]
往右排序:[11] 19 45 13 28 18 19 [77 77 81]
向左排序:[11 13] 19 45 18 28 19 [77 77 81]
往右排序:[11 13] 19 18 28 19 [45 77 77 81]
向左排序:[11 13 18] 19 19 28 [45 77 77 81]
往右排序:[11 13 18] 19 19 [28 45 77 77 81]
向左排序:[11 13 18 19 19] [28 45 77 77 81]
如上所示,括号中表示左右两边已排序完成的部份,当left > right时,则排序完成。
实作
C
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {int t; t = x; x = y; y = t;} void shakersort(int[]); int main(void) { int number[MAX] = {0}; int i; srand(time(NULL));
系列好文,点击链接即可跳转
C语言经典算法-5
约瑟夫问题(Josephus Problem)、排列组合、格雷码(Gray Code)、产生可能的集合、m元素集合的n个元素子集
C语言经典算法-7
排序法 - 改良的选择排序、快速排序法(一)、快速排序法(二)、快速排序法(三)、合并排序法
相关文章:
C语言经典算法-6
文章目录 其他经典例题跳转链接31.数字拆解32.得分排行33.选择、插入、气泡排序34.Shell 排序法 - 改良的插入排序35.Shaker 排序法 - 改良的气泡排序 其他经典例题跳转链接 C语言经典算法-1 1.汉若塔 2. 费式数列 3. 巴斯卡三角形 4. 三色棋 5. 老鼠走迷官(一&…...
【计算机考研】杭电 vs 浙工大 怎么选?
想求稳上岸的话,其他几所学校也可以考虑,以留在本地工作的角度考虑,这几所学校都能满足你的需求。 如果之后想谋求一份好工作,肯定优先杭电是比较稳的,当然复习的时候也得加把劲。 这个也可以酌情考虑,报…...
激活函数
优秀的激活函数: 非线性:激活函数非线性时,多层神经网络可逼近所有函数 可微性:梯度下降更新参数 单调性:当激活函数是单调的,能保证单层网络的损失函数是凸函数 近似恒等性:当参数初始化为…...

使用Jackson进行 JSON 序列化和反序列化
在Spring应用程序中,您可以通过Maven添加Jackson依赖,并创建一个工具类来封装对象的序列化和反序列化方法。以下是详细步骤: 1. 引入 Jackson 依赖 如果使用 Maven,您可以在 pom.xml 文件中添加以下依赖: <depend…...

Linux/Uinx 系统编程:定时器以及时钟同步
本章讨论了定时器和定时器服务;介绍了硬件定时器的原理和基于Intel x86 的PC中的硬件定时器;讲解了CPU操作和中断处理;描述了Linux中与定时器相关的系统调用、库函数和定时器服务命令;探讨了进程间隔定时器、定时器生成的信号,并通过示例演示了进程间隔定时器。编程…...
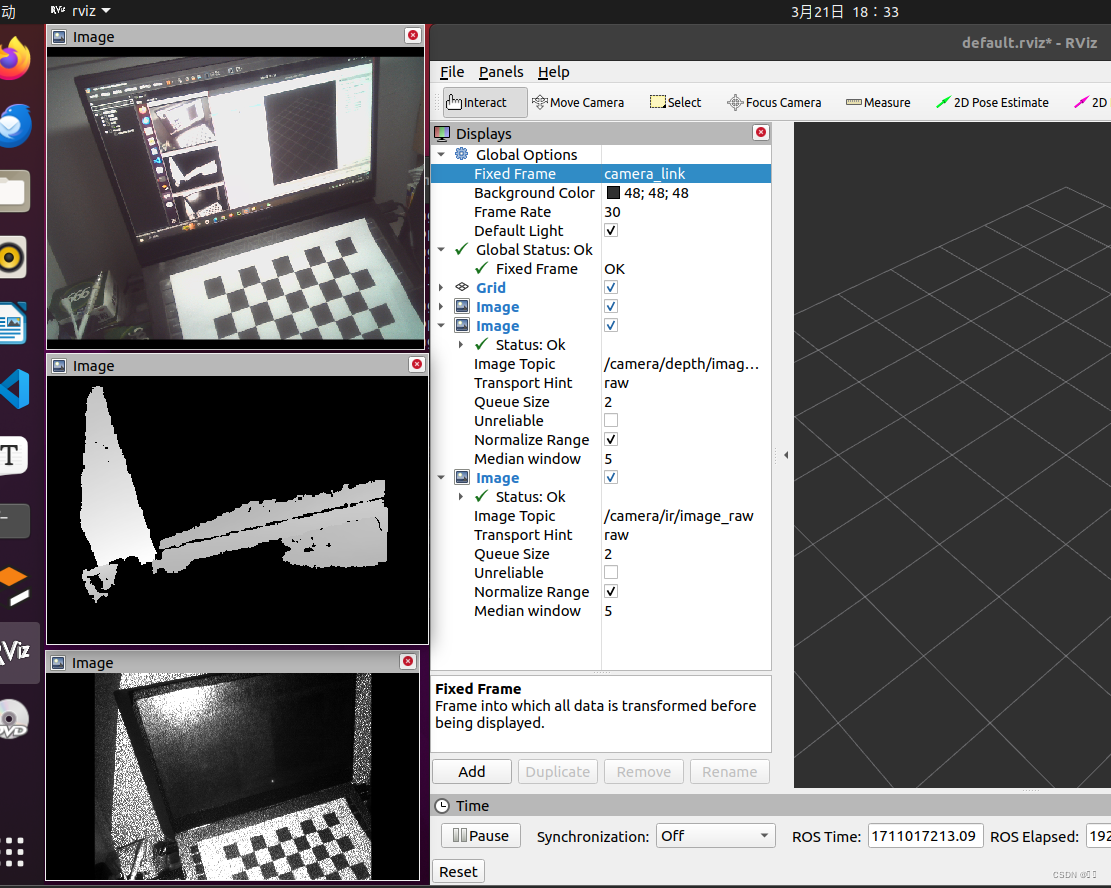
(Ubuntu中调用相机花屏)Astra plus深度相机--rgb彩色图像花屏解决方法之一
在调试深度相机的过程中只能能调出深度图像和红外图像 在rviz的image的topic中选择彩色图像的话题不显示图像 1、查看相机的usb序列号 lsusb如上图所示,此相机的USB序列号是2bc5:050f,2bc5:060f 其中050f是显示彩色图像的 在这里可通过拔插相机来确定序列号是哪几…...

iPaaS平台能帮助企业解决什么问题?
随着数字化转型的推进,越来越多的企业开始关注如何提高业务效率和灵活性。iPaaS作为一种新型集成平台,它能够帮助企业解决许多与应用程序和数据集成相关的问题。 它能给企业解决什么问题? 以下是 iPaaS 平台通常能够帮助企业解决的一些问题…...
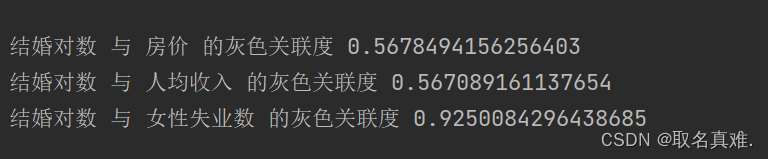
数学建模(灰色关联度 python代码 案例)
目录 介绍: 模板: 案例:哪些原因影响结婚率 数据标准化: 灰色关联度系数: 完整代码: 结果: 介绍: 灰色关联度是一种多指标综合评价方法,用于分析和评价不同指标之…...
【DP】第十四届蓝桥杯省赛C++ B组《接龙数列》(C++)
【题目描述】 对于一个长度为 K 的整数数列:A1,A2,...,AK,我们称之为接龙数列当且仅当 的首位数字恰好等于 的末位数字 (2≤i≤K)。 例如 12,23,35,56,61,11 是接龙数列;12,23,34,56 不是接龙数列,因为 56 的首位数字不等于 3…...
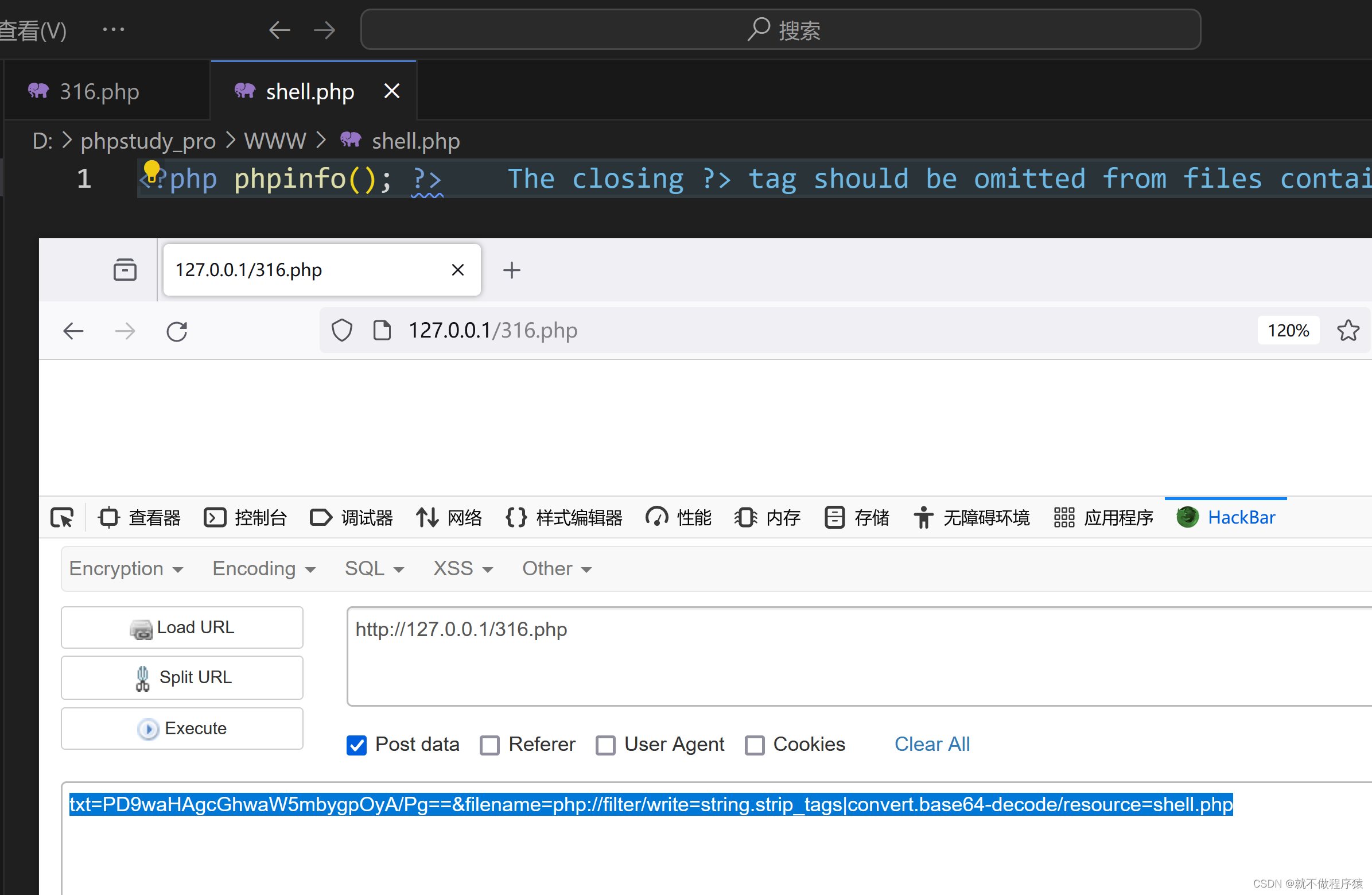
文件包含漏洞(input、filter、zip)
一、PHP://INPUT php://input可以访问请求的原始数据的只读流,将post请求的数据当作php代码执行。当传入的参数作为文件名打开时,可以将参数设为php://input,同时post想设置的文件内容,php执行时会将post内容当作文件内容。从而导致任意代码…...
使用iconv解决Linux/Ubuntu/Debian中gb2312中文文档乱码问题
你可以使用 iconv 命令行工具将文件中的文本从 GB2312 转换为 UTF-8。 你可以这样做: iconv -f GB2312 -t UTF-8 input.txt > output.txt将 input.txt 替换为以 GB2312 编码的输入文件的名称,将 output.txt 替换为你想要的 UTF-8 格式转换文件的名称。…...

图论中的最小生成树:Kruskal与Prim算法深入解析
🎬慕斯主页:修仙—别有洞天 ♈️今日夜电波:アンビバレント—Uru 0:24━━━━━━️💟──────── 4:02 🔄 ◀️ ⏸ ▶️ ☰ …...
)
uniapp 之 实现商品详情的锚点跳转(类似京东商品详情-点击顶部按钮跳转的对应的页面的内容区域)
类似京东商品详情-点击顶部详情跳转到页面对应的详情区域,点击评价跳转到页面对应的评价区域等。 照例,先封装方法: 封装方法 util.js /*** 锚点跳转(如:商品详情页面跳转)* param {string} targetId 目…...
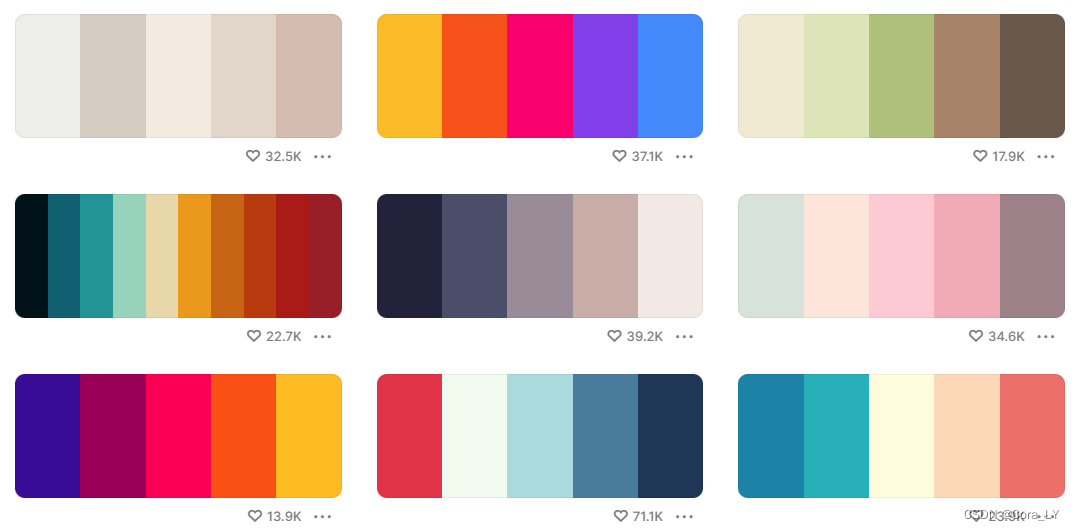
PPT好看配色
放几个链接!画图时候可以参考!转自知乎 Color Hunt ColorDrop 中国色 Flat UI Colors Coolors...
与浏览器环境有何不同)
微信小程序执行环境(微信端)与浏览器环境有何不同
微信小程序执行环境与浏览器环境有很多不同之处,以下是一些例子: 全局对象: 浏览器环境中的 JavaScript 有一个全局对象 window,而微信小程序中的 JavaScript 没有 window 对象,取而代之的是 wx 对象,wx …...

Java小项目--满汉楼
Java小项目–满汉楼 项目需求 项目实现 1.实现对工具包的编写 先创建libs包完成对jar包的拷贝和添加入库 德鲁伊工具包 package com.wantian.mhl.utils;import com.alibaba.druid.pool.DruidDataSourceFactory;import javax.sql.DataSource; import java.io.FileInputStream…...
微信怎样群发更高效?
群发是指通过微信平台对特定受众进行大规模信息发布的过程,如节日祝福、活动促销等。随着科技的不断发展,群发的定义已不再仅限于手机信息群发或短信群发。如今,微信内置的群发功能也被广泛应用。 一、微信群发的操作步骤 1. 进入微信&…...
javaSwing愤怒的小鸟
一、简介 游戏名称是“愤怒的小鸟”,英文称为“AngryBird”。 “愤怒的小鸟”是著名游戏公司Rovio偶然间开发出来的益智游戏,从2009年12月上市到iOS。,讲述了鸟类和猪因为猪偷鸟蛋反生的一系列故事。游戏的类型版本是横向版本的水平视角&…...
)
10 开源鸿蒙中芯片与开发板对应的源码(硬件相关的部分)
开源鸿蒙中芯片与开发板对应的源码(硬件相关的部分) 作者将狼才鲸日期2024-03-20 开源鸿蒙通过芯片仓存放指定芯片和指定开发板的代码,硬件相关的代码和纯逻辑代码是分开存放的 源码模块的组织结构在manifest这个Git仓库,这也是拉…...
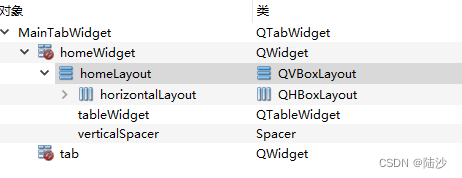
qt5-入门-标签页部件QTabWidget-1
参考: C GUI Programming with Qt 4, Second Edition 本地环境: win10专业版,64位,Qt5.12 目录 效果实现Qt Designer操作代码addStretch()解释 效果 首页有三个按钮和最近文件列表。 拖动窗口,按钮和文件列表仍然处…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...

JavaScript 标签加载
目录 JavaScript 标签加载script 标签的 async 和 defer 属性,分别代表什么,有什么区别1. 普通 script 标签2. async 属性3. defer 属性4. type"module"5. 各种加载方式的对比6. 使用建议 JavaScript 标签加载 script 标签的 async 和 defer …...
