图论中的最小生成树:Kruskal与Prim算法深入解析

🎬慕斯主页:修仙—别有洞天
♈️今日夜电波:アンビバレント—Uru
0:24━━━━━━️💟──────── 4:02
🔄 ◀️ ⏸ ▶️ ☰
💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍
目录
最小生成树
Kruskal算法
如何理解Kruskal算法?
Kruskal算法的实现
Prim算法
如何理解Prim算法?
Prim算法的实现
最小生成树
最小生成树(Minimum Spanning Tree,简称 MST)是一个无向连通图中包含所有顶点的边的权值之和最小的子图。它有以下特点:
- 包含原图所有顶点:最小生成树是一个生成树,因此它必须包含图中的所有顶点。
- 边的权值之和最小:在所有的生成树中,最小生成树是边的权值总和最小的那一个。
- 是无环的:作为一棵树,最小生成树中不存在环,即任意两个顶点之间有且仅有一条路径相连。
求解最小生成树的常用算法有两种:
- Kruskal算法:该算法的基本思想是按照边的权值从小到大的顺序选择边,如果这条边连接的两个顶点不在同一个连通分量中,则加入这条边,直到所有顶点都被包含在内。这个过程中,使用并查集数据结构来判断两个顶点是否属于同一个连通分量是非常有效的。
- Prim算法:与Kruskal算法不同,Prim算法是一种贪心算法,它从任意一个顶点开始,每一步都选择连接当前已选取顶点集合与未选取顶点集合之间权值最小的边,并将其加入到最小生成树中,直到所有顶点都被包含。
总的来说,最小生成树的概念在许多领域都有应用,如网络设计、交通规划等,它可以帮助找到成本最低的连接方案。
Kruskal算法
如何理解Kruskal算法?
Kruskal算法是一种用来寻找最小生成树的贪心算法,它的核心思想是选择边权值之和最小的同时不会形成环路的边来构建最小生成树。(使用的就是全局的贪心策略)具体步骤如下:
- 边的排序:将图中的所有边按照权值从小到大进行排序。(这一步我们可以使用到优先级队列)
- 初始化并查集:使用并查集数据结构来记录各个顶点的连通性,初始时每个顶点自成一个集合。
- 遍历边并检查环路:按权值从小到大的顺序遍历每条边,利用并查集判断这条边连接的两个顶点是否属于不同的集合。如果是,则加入这条边并不会形成环路,因此将其加入到最小生成树中,并将这两个顶点所在的集合合并。
- 重复直至完成:重复上述步骤,直到添加了V-1条边(V为图中顶点的数量),此时便形成了包含所有顶点的最小生成树。
需要注意的是,在应用Kruskal算法时,需要确保图是连通的,因为算法只能处理连通图的最小生成树问题。如果图不是连通的,那么需要先对图进行连通分量的分析,然后对每个连通分量分别求解最小生成树。大致图解如下:

Kruskal算法的实现
本文的Kruskal算法是在邻接矩阵的基础上进行实现的,邻接矩阵的实现参考上一篇文章,这里先实现边的结构体,给定两个size_t类型表示源地址_srcI以及目标地址_dstI(实际上就是对应顶点的下标),根据模版类型W来存储边的权值_w,并且重载了一个>符,用于后续优先级队列中对于伪函数的使用,实现如下:
struct Edge{size_t _srci;size_t _dsti;W _w;Edge(size_t srci, size_t dsti, const W& w):_srci(srci), _dsti(dsti), _w(w){}bool operator>(const Edge& e) const{return _w > e._w;}};需要注意:前面我们将整个邻接矩阵都已经重新命名了,这样做是为了更好的定义最小生成树,毕竟他本质上也是一个图,并且也是在原来的基础上定义的,我们当然可以使用原来的数据结构:
typedef Graph<V, W, MAX_W, Direction> Self;接下来,按照上述的实现步骤一步一步实现:(1)初始化,由于最小生成树对于原图可能只是变小于等于原图,其他实际上都是一样的。因此,我们可以根据原图进行初始化,顶点的存储、顶点同下标的映射都是一样的,只是边需要重新构建!其中MAX_W是作为初始化边的值,默认为INT_MAX。(2)使用优先级队列,以升序的方式对上面我们构建的边结构体进行排序,将原图的所有边都放入优先级队列!(3)选出n-1条边,首先定义一个变量size用于储存有多少条边被选,定义一个totalW用于储存权值,定义一个并查集ufs用于查环。每次遍历都会将优先级队列的顶部值取出,上一篇文章中提到过InSet是用于判断是否为同一根节点(判环)的操作,若不为环则按照邻接矩阵的方法构造边,并且也在并查集中合并在一起。(4)这个循环中不论如何都会将优先级队列中的值全部释放,然后退出循环,最后根据size来判断是否可以形成最小生成树并且返回权值。如下为具体的实现:
W Kruskal(Self& minTree){size_t n = _vertexs.size();minTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(n);for (size_t i = 0; i < n; ++i){minTree._matrix[i].resize(n, MAX_W);}priority_queue<Edge, vector<Edge>, greater<Edge>> minque;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (i < j && _matrix[i][j] != MAX_W){minque.push(Edge(i, j, _matrix[i][j]));}}}// 选出n-1条边int size = 0;W totalW = W();UnionFindSet ufs(n);while (!minque.empty()){Edge min = minque.top();minque.pop();if (!ufs.InSet(min._srci, min._dsti)){cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;minTree._AddEdge(min._srci, min._dsti, min._w);ufs.Union(min._srci, min._dsti);++size;totalW += min._w;}else{cout << "构成环:";cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;}}if (size == n - 1){return totalW;}else{return W();}}Prim算法
如何理解Prim算法?
Prim算法是一种用于求解加权连通无向图中最小生成树的算法。它的核心思想是从一个顶点开始,逐步扩展已选取的顶点集合,直到所有顶点都被包含在内。(使用的就是局部的贪心策略)具体步骤如下:
- 选择起始点:从图中任意选择一个顶点作为起始点。
- 构建边界集:将起始点加入已选取的顶点集合中,同时维护一个边界顶点集合,这些顶点是已选取顶点集合与未选取顶点集合之间的边界。
- 选择轻量级边:在边界集合中选择权值最小的边,将该边以及其连接的未选取顶点加入到已选取集合中。
- 更新边界集:更新边界集合,将新加入的顶点作为新的边界顶点。
- 重复直至完成:重复步骤3和步骤4,直到所有顶点都被加入到已选取的顶点集合中,此时形成的树即为最小生成树。
总的来说,Prim算法的关键在于每一步都选择当前最优的选择,即权值最小的边,以此来保证最终得到的是最小生成树。这种贪心策略确保了算法的效率和结果的最优性。大致图解如下:

Prim算法的实现
由于Prim是由局部逐步扩散到全局的,也就是说他并不会选择到选过的顶点,因此Prim的实现并不需要使用到并查集。对于上面Kruskal提到的Edge以及Self不多阐述。
由于Prim需要指定一个顶点开始,因此接口相对Kruskal多传了一个顶点。接下来,按照上述的实现步骤一步一步实现:(1)初始化,同Kruskal一样,我们都是使用邻接矩阵来实现的,因此前期初始化是相同的操作,接着,获取对应的顶点下标映射,创建两个bool数组分别用于表示已选取的顶点集合和未选取顶点集合,true表示拥有该顶点,false表示不拥有。最后按照下标映射初始化两个数组,选取的则改为true,未选改为false,完成初始化。(2)使用优先级队列先将开始顶点的边放入队列中,同样设置size和totalW。(3)开始选边,出队列顶的边,通过判断是否在已选取的顶点集合来判断是否可选(可以变相理解为是否成环),如果不在表示为没有选过因此可以选,选取后将已选取的顶点集合和未选取顶点集合分别改变,再根据刚刚选取的点选取他临界的顶点。(4)在这个循环中,可能会出现很多重复的点的情况,但是我们有已选取的顶点集合来判断是否可选,这样不可选的会自动出队列而不被选取,最后根据size来判断是否可以形成最小生成树并且返回权值。
具体实现如下:
W Prim(Self& minTree, const W& src){size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();minTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(n);for (size_t i = 0; i < n; ++i){minTree._matrix[i].resize(n, MAX_W);}/*set<int> X;set<int> Y;X.insert(srci);for (size_t i = 0; i < n; ++i){if (i != srci){Y.insert(i);}}*/vector<bool> X(n, false);vector<bool> Y(n, true);X[srci] = true;Y[srci] = false;// 从X->Y集合中连接的边里面选出最小的边priority_queue<Edge, vector<Edge>, greater<Edge>> minq;// 先把srci连接的边添加到队列中for (size_t i = 0; i < n; ++i){if (_matrix[srci][i] != MAX_W){minq.push(Edge(srci, i, _matrix[srci][i]));}}cout << "Prim开始选边" << endl;size_t size = 0;W totalW = W();while (!minq.empty()){Edge min = minq.top();minq.pop();// 最小边的目标点也在X集合,则构成环if (X[min._dsti]){//cout << "构成环:";//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;}else{minTree._AddEdge(min._srci, min._dsti, min._w);//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;X[min._dsti] = true;Y[min._dsti] = false;++size;totalW += min._w;if (size == n - 1)break;for (size_t i = 0; i < n; ++i){if (_matrix[min._dsti][i] != MAX_W && Y[i]){minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));}}}}if (size == n - 1){return totalW;}else{return W();}}
感谢你耐心的看到这里ღ( ´・ᴗ・` )比心,如有哪里有错误请踢一脚作者o(╥﹏╥)o!

给个三连再走嘛~
相关文章:

图论中的最小生成树:Kruskal与Prim算法深入解析
🎬慕斯主页:修仙—别有洞天 ♈️今日夜电波:アンビバレント—Uru 0:24━━━━━━️💟──────── 4:02 🔄 ◀️ ⏸ ▶️ ☰ …...
)
uniapp 之 实现商品详情的锚点跳转(类似京东商品详情-点击顶部按钮跳转的对应的页面的内容区域)
类似京东商品详情-点击顶部详情跳转到页面对应的详情区域,点击评价跳转到页面对应的评价区域等。 照例,先封装方法: 封装方法 util.js /*** 锚点跳转(如:商品详情页面跳转)* param {string} targetId 目…...
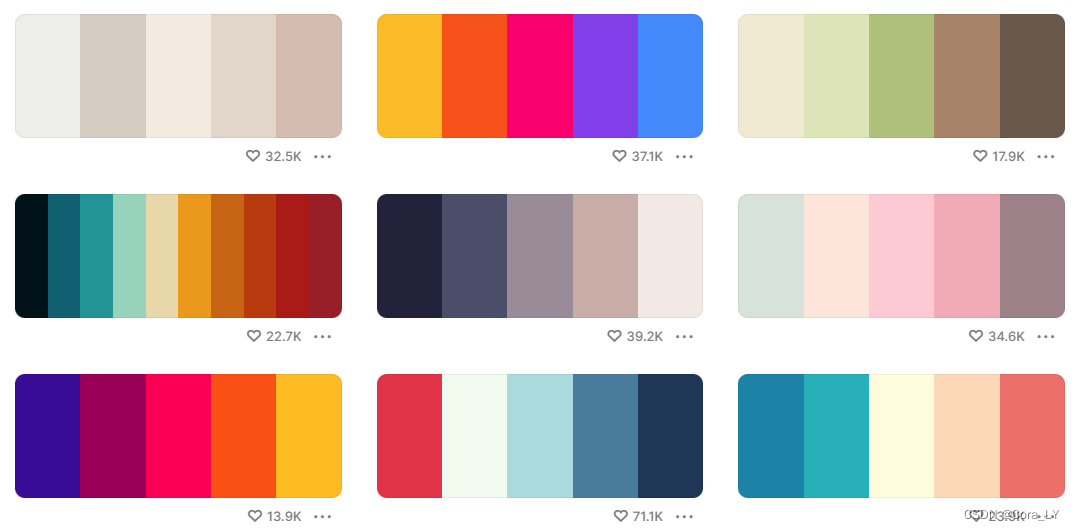
PPT好看配色
放几个链接!画图时候可以参考!转自知乎 Color Hunt ColorDrop 中国色 Flat UI Colors Coolors...
与浏览器环境有何不同)
微信小程序执行环境(微信端)与浏览器环境有何不同
微信小程序执行环境与浏览器环境有很多不同之处,以下是一些例子: 全局对象: 浏览器环境中的 JavaScript 有一个全局对象 window,而微信小程序中的 JavaScript 没有 window 对象,取而代之的是 wx 对象,wx …...

Java小项目--满汉楼
Java小项目–满汉楼 项目需求 项目实现 1.实现对工具包的编写 先创建libs包完成对jar包的拷贝和添加入库 德鲁伊工具包 package com.wantian.mhl.utils;import com.alibaba.druid.pool.DruidDataSourceFactory;import javax.sql.DataSource; import java.io.FileInputStream…...
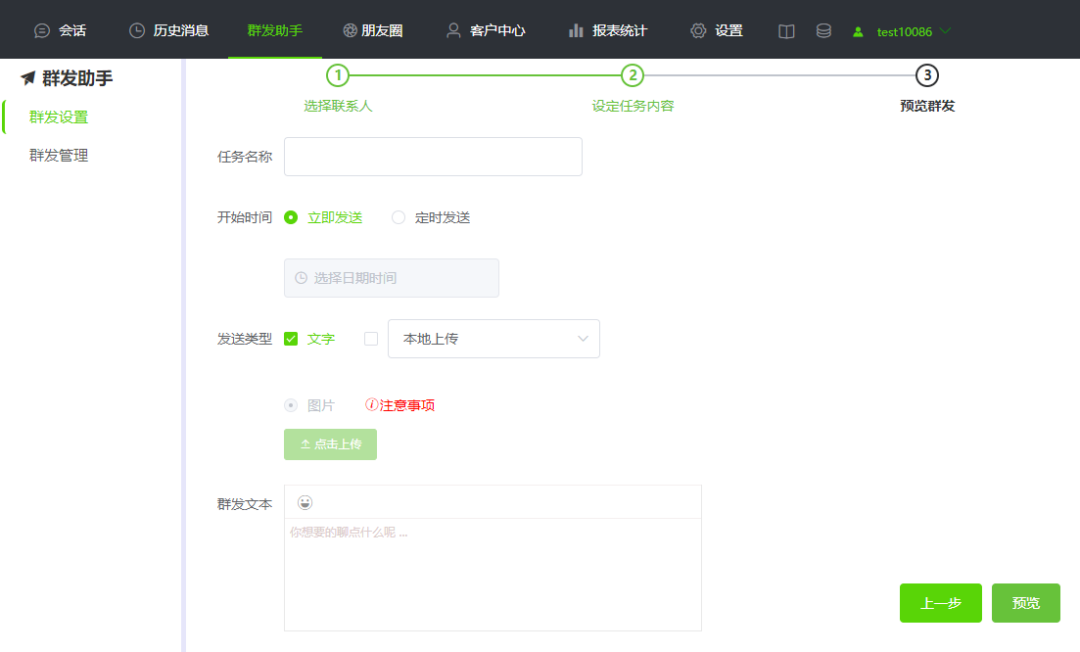
微信怎样群发更高效?
群发是指通过微信平台对特定受众进行大规模信息发布的过程,如节日祝福、活动促销等。随着科技的不断发展,群发的定义已不再仅限于手机信息群发或短信群发。如今,微信内置的群发功能也被广泛应用。 一、微信群发的操作步骤 1. 进入微信&…...
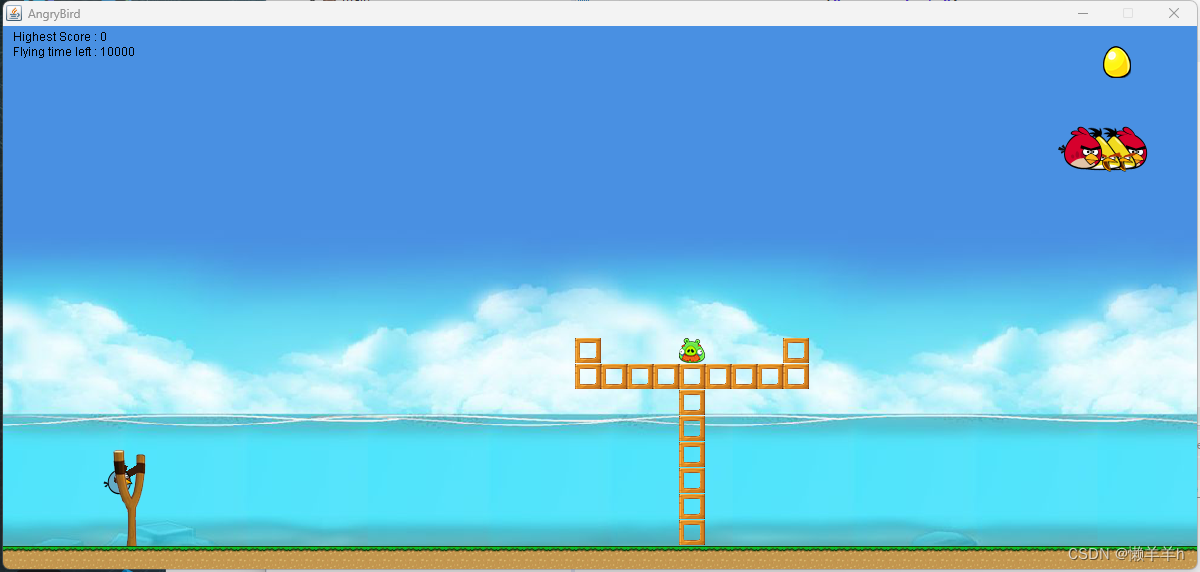
javaSwing愤怒的小鸟
一、简介 游戏名称是“愤怒的小鸟”,英文称为“AngryBird”。 “愤怒的小鸟”是著名游戏公司Rovio偶然间开发出来的益智游戏,从2009年12月上市到iOS。,讲述了鸟类和猪因为猪偷鸟蛋反生的一系列故事。游戏的类型版本是横向版本的水平视角&…...
)
10 开源鸿蒙中芯片与开发板对应的源码(硬件相关的部分)
开源鸿蒙中芯片与开发板对应的源码(硬件相关的部分) 作者将狼才鲸日期2024-03-20 开源鸿蒙通过芯片仓存放指定芯片和指定开发板的代码,硬件相关的代码和纯逻辑代码是分开存放的 源码模块的组织结构在manifest这个Git仓库,这也是拉…...
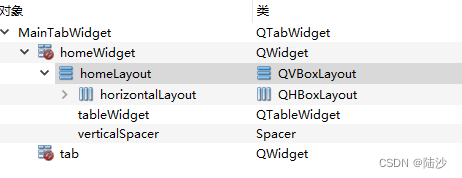
qt5-入门-标签页部件QTabWidget-1
参考: C GUI Programming with Qt 4, Second Edition 本地环境: win10专业版,64位,Qt5.12 目录 效果实现Qt Designer操作代码addStretch()解释 效果 首页有三个按钮和最近文件列表。 拖动窗口,按钮和文件列表仍然处…...

GOPS全球运维大会2024深圳站亮点抢先看!
2024年4月25-26日,博睿数据将受邀出席第二十二届 GOPS 全球运维大会深圳站。本次大会上,博睿数据AIOps首席专家兼产品总监贺安辉将亮相AIOps最佳实践及解决方案专场,分享《一体化智能可观测平台的两翼:数据模型AI算法》的主题演讲…...

给wordpress添加自定义字段的分类筛选功能
要为WordPress添加自定义字段的筛选功能,你需要使用WordPress的查询参数(query parameters)和WP_Query类来构建自定义查询。以下是一个详细的示例代码,展示了如何添加自定义字段的筛选功能。 首先,你需要在你的主题或插件的functions.php文件…...
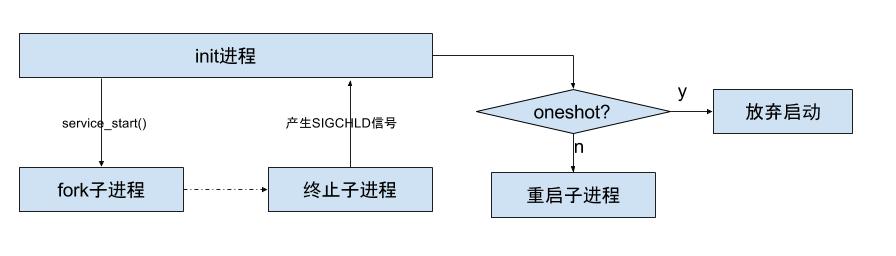
Android 系统的启动过程
Android 系统的启动流程: RomBoot(只读存储器引导程序):这是设备上电时运行的初始软件。RomBoot执行基本的硬件初始化,确保硬件处于可以运行后续启动阶段的状态。这一阶段非常重要,因为它为整个启动过程奠定…...
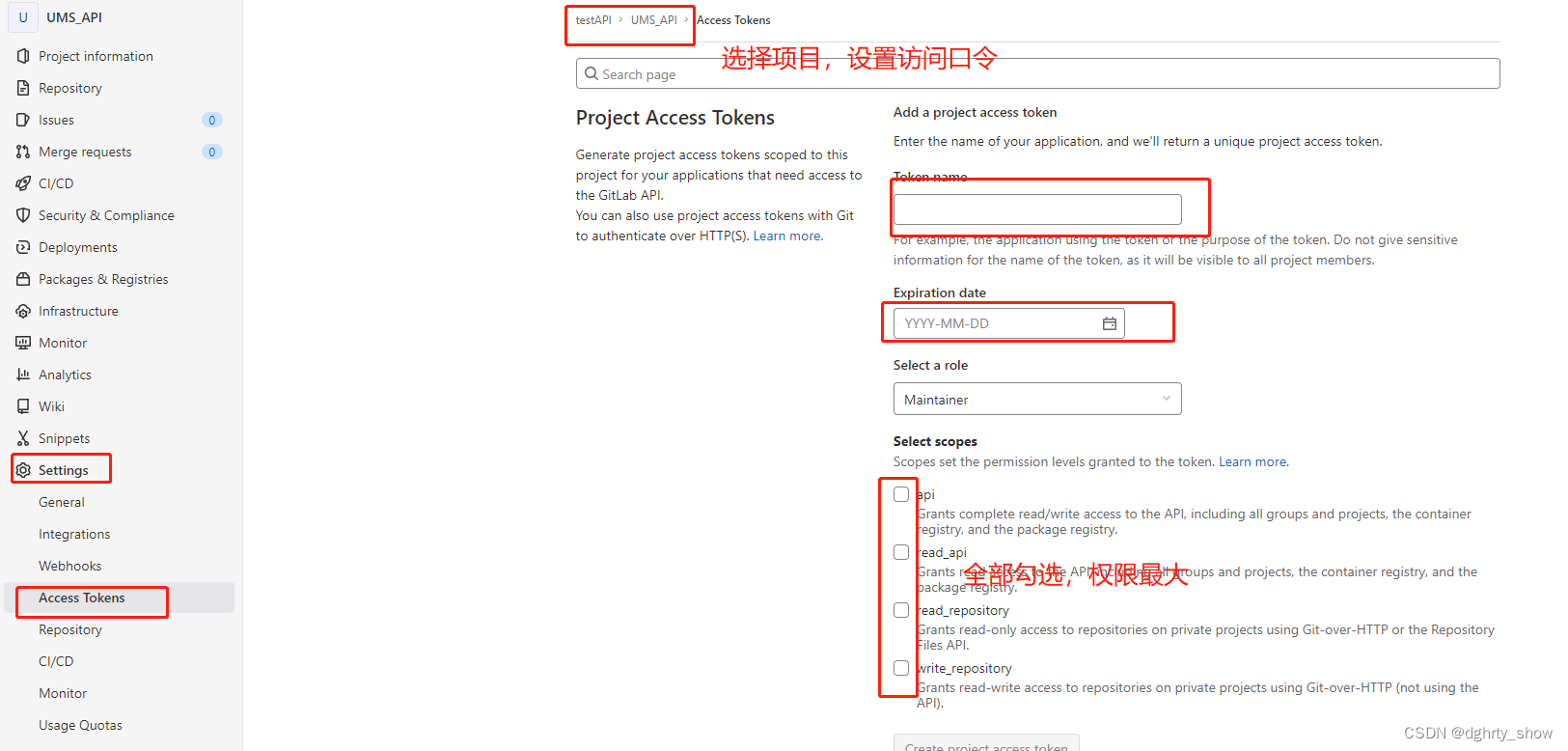
jenkins配置源码管理的git地址时,怎么使用不了 credential凭证信息
前提 Jenkins使用docker部署 问题 (在jenlins中设置凭证的方式)在Jenkins的任务重配置Git地址,并且设置了git凭证,但是验证不通过,报错; 无法连接仓库:Command "git ls-remote -h -- http://192.1XX.0.98:X02/…...

Emotion Prompt-LLM能够理解并能通过情感刺激得以增强
Large Language Models Understand and Can be Enhanced by Emotional Stimuli 情感智能对我们的日常行为和互动产生了显著的影响。尽管大型语言模型(LLMs)被视为向人工通用智能迈进的一大步,在许多任务中表现出色,但目前尚不清楚…...
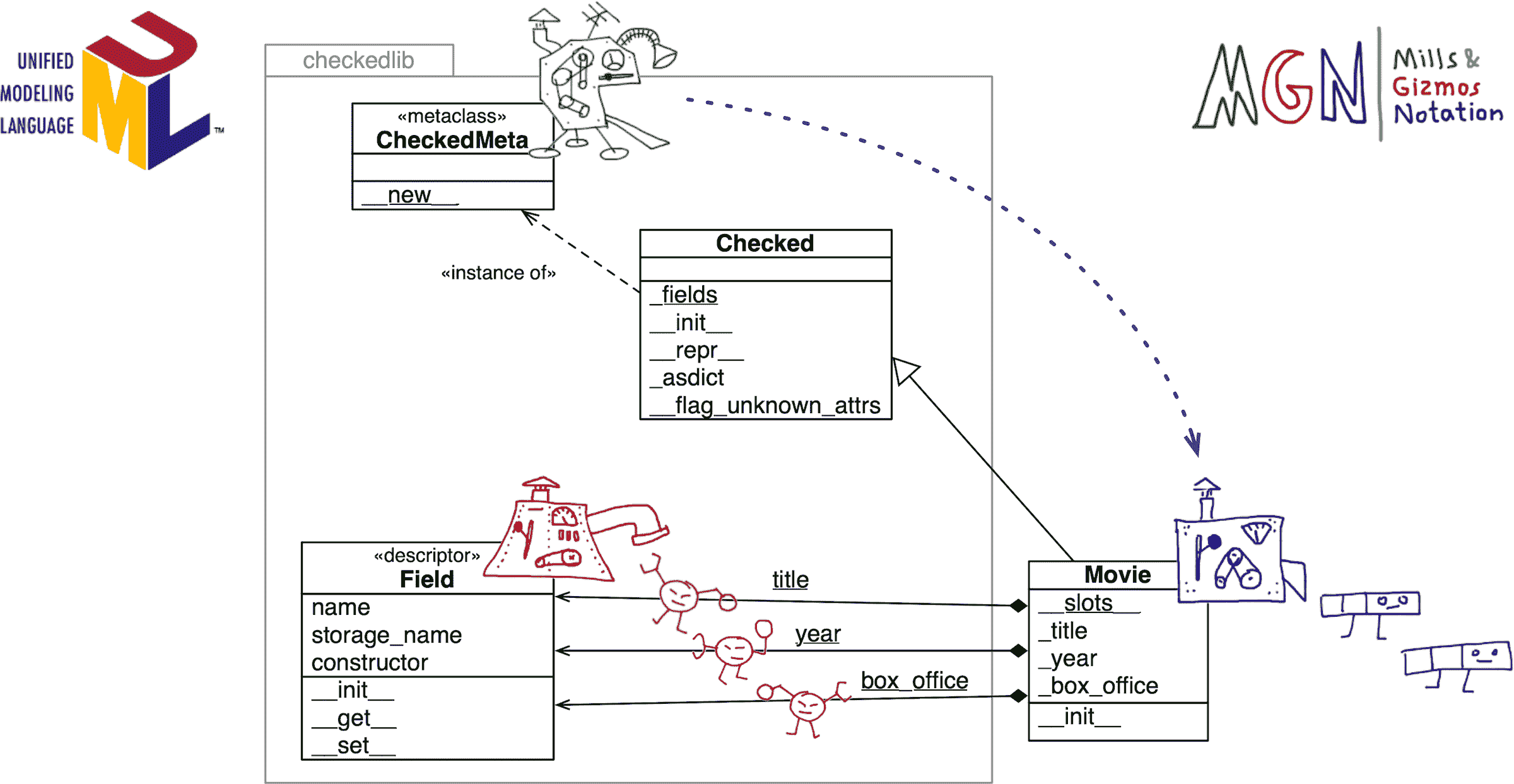
流畅的 Python 第二版(GPT 重译)(十三)
第二十四章:类元编程 每个人都知道调试比一开始编写程序要困难两倍。所以如果你在编写时尽可能聪明,那么你将如何调试呢? Brian W. Kernighan 和 P. J. Plauger,《编程风格的要素》 类元编程是在运行时创建或自定义类的艺术。在 P…...

C/C++炸弹人游戏
参考书籍《啊哈,算法》,很有意思的一本算法书,小白也可以看懂,详细见书,这里只提供代码和运行结果。 这里用到的是枚举思想,还有更好地搜索做法。 如果大家有看不懂的地方或提出建议,欢迎评论区…...

③【Docker】Docker部署Nginx
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ ③【Docker】Docker部署Nginx docker拉取nginx…...
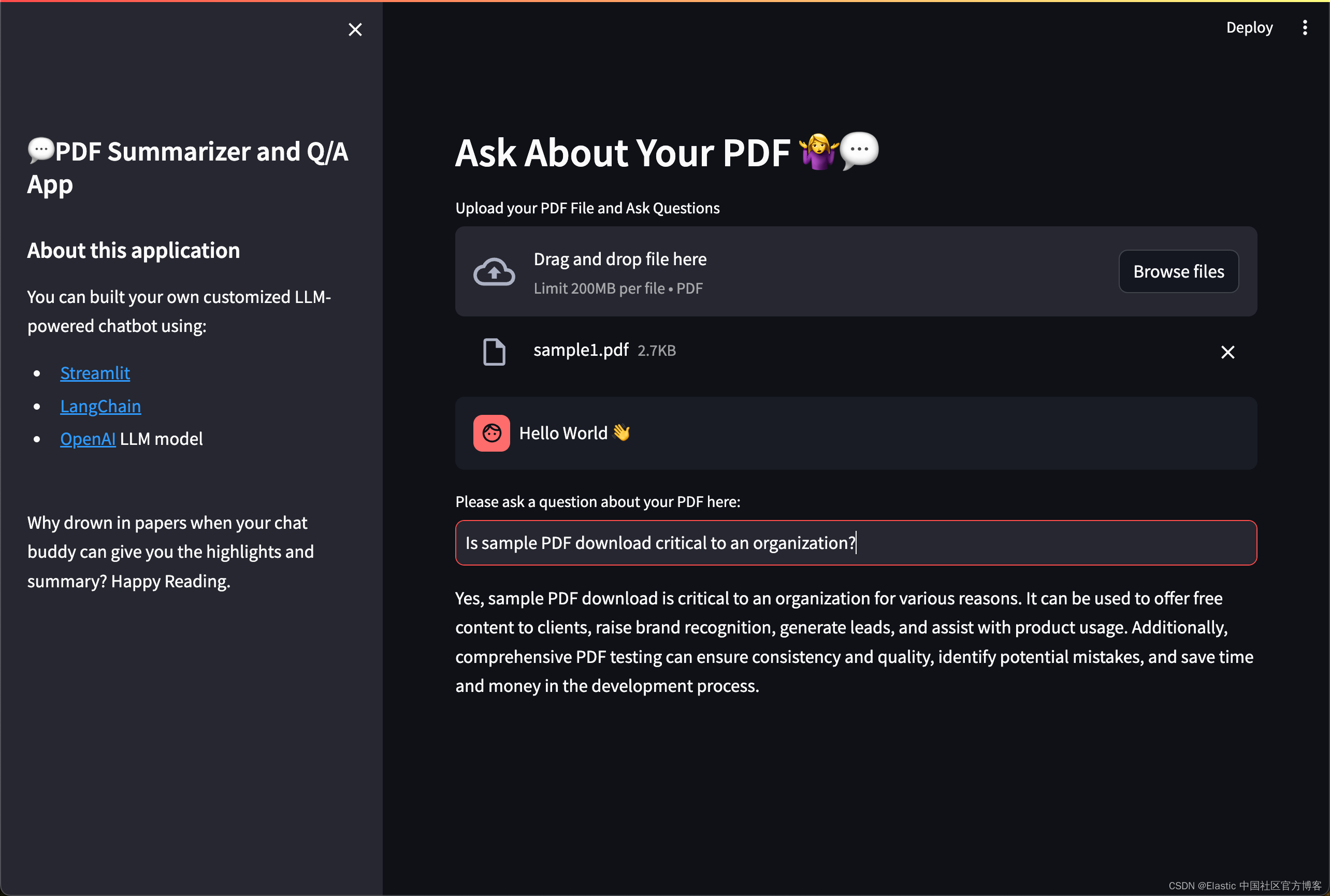
Elasticsearch:使用 OpenAI、LangChain 和 Streamlit 的基于 LLM 的 PDF 摘要器和 Q/A 应用程序
嘿! 您是否曾经感觉自己被淹没在信息的海洋中? 有这么多的书要读,而时间却这么少,很容易就会超负荷,对吧? 但猜猜怎么了? 你可以使用大型语言模型创建自定义聊天机器人,该模型可以帮…...

Linux课程____进程管理
记录工作日志 script 240319.log CTRLd 退出 cat 240319.log //查看 一、查看进程 1.静态 ps -aux 显示所有包含其他使用者的行程 ps -elf 2.动态 top 3.pgrep 查看特定条件的进程 pgrep -l “log” 搜索特定的程序 pgrep -l "ssh" pgrep -l -U…...
算法设计与分析-动态规划算法的应用——沐雨先生
一、实验目的 1. 掌握动态规划算法的基本思想,包括最优子结构性质和基于表格的最优值计算方法。 2.熟练掌握分阶段的和递推的最优子结构分析方法。 3. 学会利用动态规划算法解决实际问题 。 二、实验内容 1. 问题描述 &#…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
