【链表】Leetcode 19. 删除链表的倒数第 N 个结点【中等】
删除链表的倒数第 N 个结点
- 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
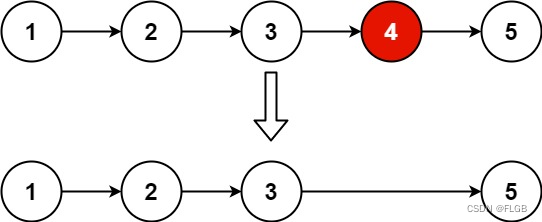
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
解题思路
- 1、使用快慢指针找到要删除节点的前一个节点。
- 2、删除目标节点。
具体步骤
- 初始化两个指针 first 和 second,都指向链表的头节点。
- 将 first 移动到第 n 个节点。
- 然后同时移动 first 和 second,直到 first 指向链表末尾。
- 此时 second 的下一个节点就是要删除的节点,
- 将 second.next 指向 second.next.next
java实现
public class RemoveNthFromEnd {public ListNode removeNthFromEnd(ListNode head, int n) {ListNode dummy = new ListNode(0);dummy.next = head;ListNode first = dummy;ListNode second = dummy;// 将 first 移动到第 n 个节点for (int i = 0; i <= n; i++) {first = first.next;}// 同时移动 first 和 second,直到 first 指向末尾while (first != null) {first = first.next;second = second.next;}// 删除倒数第 n 个节点second.next = second.next.next;return dummy.next;}public static void main(String[] args) {// 构造链表 1 -> 2 -> 3 -> 4 -> 5ListNode head = new ListNode(1);head.next = new ListNode(2);head.next.next = new ListNode(3);head.next.next.next = new ListNode(4);head.next.next.next.next = new ListNode(5);int n = 2;// 调用 removeNthFromEnd 方法删除倒数第 n 个节点RemoveNthFromEnd solution = new RemoveNthFromEnd();ListNode result = solution.removeNthFromEnd(head, n);// 打印删除后的链表while (result != null) {System.out.print(result.val + " ");result = result.next;}// 输出:1 -> 2 -> 3 -> 5}
}
class ListNode {int val;ListNode next;ListNode(int x) {val = x;next = null;}
}
时间空间复杂度
- 时间复杂度:O(n),其中 n 是链表的长度,需要遍历一次链表。
- 空间复杂度:O(1),只需要使用常数级别的额外空间。
相关文章:

【链表】Leetcode 19. 删除链表的倒数第 N 个结点【中等】
删除链表的倒数第 N 个结点 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 示例 1: 输入:head [1,2,3,4,5], n 2 输出:[1,2,3,5] 解题思路 1、使用快慢指针找到要删除节点的前一个节点。2、删…...

亚马逊认证考试系列 - 知识点 - 安全组简介
AWS安全组是一种虚拟防火墙,用于控制实例进出网络流量。安全组是一个实例级别的防火墙,可以定义哪些流量可以进入或离开特定的EC2实例。 功能:安全组可以用于限制特定类型的流量,如HTTP或SSH,允许特定IP地址范围的流量…...
)
同向双指针合集(力扣)
283. 移动零 代码 class Solution { public:void moveZeroes(vector<int>& nums) {int n nums.size();int l 0, r 0;while(r < n){if(nums[r]){swap(nums[l],nums[r]);l;}r;}} };209. 长度最小的子数组 代码 class Solution { public:int minSubArrayLen(i…...

G - Find a way
题目分析 1.双重bfs,遍历两个起点求最短路再计算总和即可 2.唯一的坑点在于对于一个KFC,两人中可能有一个到不了,所以还要对到不了的点距离做处理 #include <bits/stdc.h> using namespace std; using ll long long; const int N 220;struct pos…...

AJAX 02 案例、Bootstrap框架
AJAX 学习 AJAX 2 综合案例黑马 API01 图书管理Bootstrap 官网Bootstrap 弹框图书管理-渲染列表图书管理-添加图书图书管理-删除图书图书管理 - 编辑图书 02 图片上传03 更换图片04 个人信息设置信息渲染头像修改补充知识点:label扩大表单的范围 AJAX 2 综合案例 黑…...
SinoDB客户端工具dbaccess
类似Oracle的客户端工具sqlplus,Mysql的客户端工具mysql,SinoDB数据库也有自带的命令行客户端工具dbaccess。 dbaccess 识别用户输入,将用户输入的 SQL 语句打包发送给 SinoDB 数据库服务器执行,然后接收服务器的执行结果…...

postman学习
一、如何学习postman工具 1、下载和安装 Postman: 首先,从 Postman 官方网站(https://www.postman.com)下载并安装 Postman 应用程序。 2、了解基本概念: 在开始学习之前,了解一些基本概念,…...
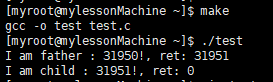
【Linux】初识进程
目录 操作系统是什么 设计操作系统的目的 操作系统的定位 如何理解管理 管理的本质 管理的例子 计算机的管理概念图 操作系统管理逻辑的六字真言 系统调用和库函数的概念 进程 进程的概念 什么是PCB? PCB的主要内容 如何查看进程? 通过系统…...

有关Theano和PyTensor库
根据Github里面的介绍,PyTensor是源于Theano, Theano目前应该已经不再开发了,更新都是很多年前。 因此PyTensor在背景介绍中说 PyTensor is a fork of Aesara, which is a fork of Theano. Theano和PyTensor都是计算相关的库,可以…...

用 Open-Sora 高效创作视频,让创意触手可及
近年来,视频内容以爆炸式增长席卷了我们的生活。从短视频平台到直播带货,视频正成为人们获取信息和娱乐的主要方式。然而,传统视频制作流程往往耗时费力,对于普通用户来说门槛较高。 为了降低视频创作门槛,让更多人享…...
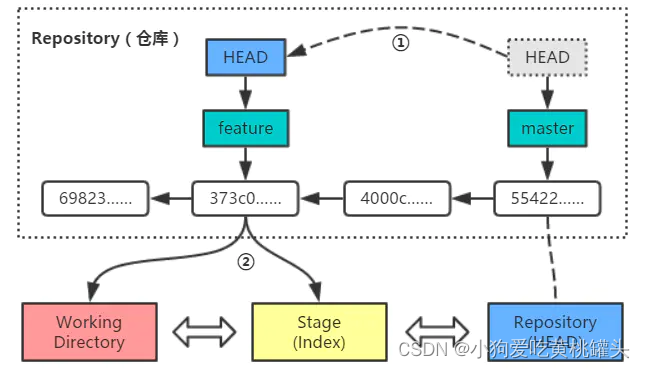
Git版本管理工具
前言: 本文记录学习使用 Git 版本管理工具的学习笔记,通过阅读参考链接中的博文和实际操作,快速的上手使用 Git 工具。 本文参考了引用链接博文里的内容。 引用: Git使用教程-配置管理 git reset详解-CSDN博客 3、Git使用不完全指南&am…...
微信小程序选择器picker的使用(省市区)
index.wxml picker中的 moderegion模式,这里同element中的select不同的是,不需要自己在绑定数据原,默认就包含了省市区的整体数据 <view class"section"><view class"section__title">省市区选择器</vie…...
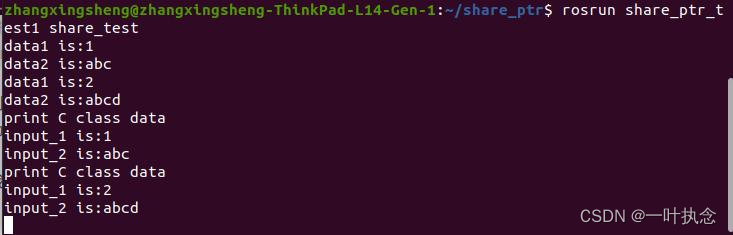
std::shared_ptr与std::make_unique在类函数中的使用
在最近学习cartographer算法的时候,发现源码中大量的使用了std::shared_ptr与std::make_unique,对于这些东西之前不是很了解,为了更好的理解源代码,因此简单学习了一下这块内容的使用,在这里简单记个笔记。 std::shar…...
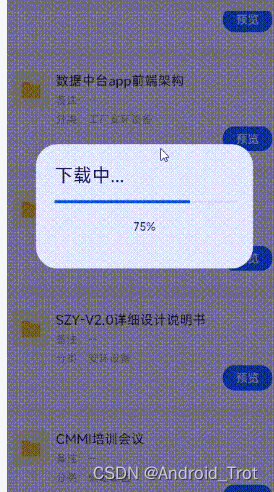
flutter 局部view更新,dialog更新进度,dialog更新
局部更新有好几种方法,本次使用的是 StatefulBuilder 定义 customState去更新对话框内容 import package:flutter/cupertino.dart; import package:flutter/material.dart;class ProgressDialog {final BuildContext context;BuildContext? dialogContext;double _…...

Lombok:@Delegate优化代码利器
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 一、Delegate介绍 二、示例 三、使用场景 四、使用注意事项 总结 提示:以下是本篇文章正文内容,下面案例可供参考 一、Delegate介绍 Dele…...

【C语言】对称密码——栅栏的加密和解密
栅栏密码的原理: 栅栏层数n ①把将要传递的信息中的字母交替排成上下n行。 ②再将下面每一行字母排依次在上面一行的后边,从而形成一段密码。 ③例如:栅栏层数为2 明文:THE LONGEST DAY MUST HAVE AN END 加密: …...
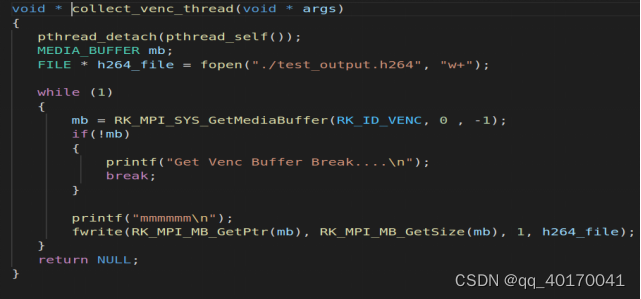
一、rv1126开发之视频输入和视频编码
RV1126 H264/HEVC编码流程 一、RV1126编码的流程图: 二、每个代码模块详细讲解 2.1. VI模块的创建 VI模块的初始化:关键在于VI_CHN_ATTR_S结构体,这个结构体是VI设置的结构体。这个结构体的成员变量包括:pcVideoNode࿰…...
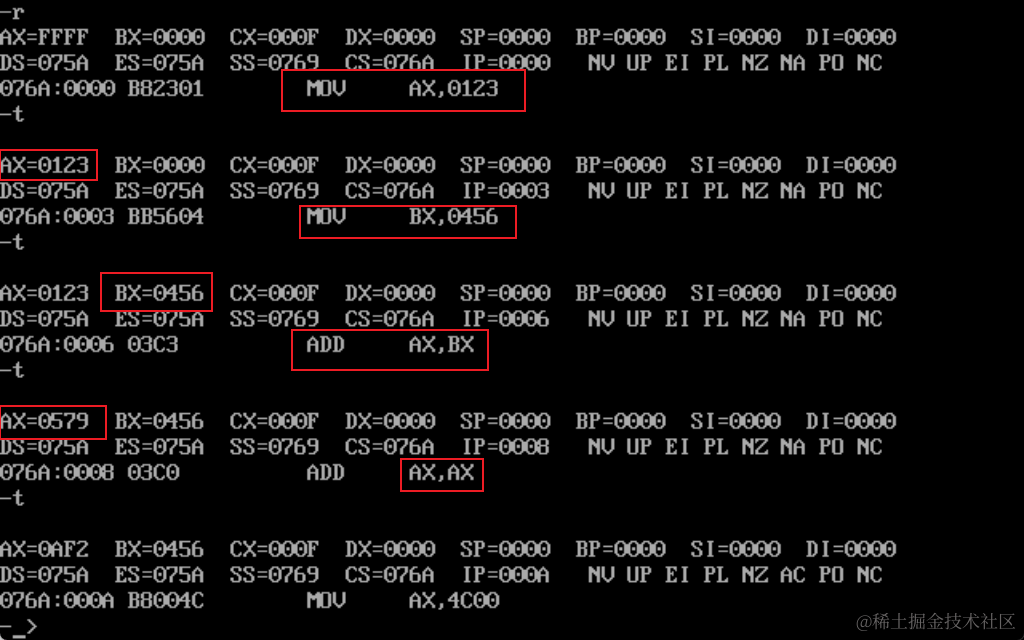
4.1 用源文件写汇编代码
汇编语言 1. 源程序 1.1 伪指令 汇编指令是有对应的机器码的指令,可以被编译为机器指令,最终为CPU所执行伪指令没有对应的机器指令,最终不被CPU所执行伪指令是由编译器来执行的指令,编译器根据伪指令来进行相关的编译工作 1.2…...

Linux TCP参数——tcp_abort_on_overflow
文章目录 tcp_abort_on_overflow全连接队列是什么?如何改变队列大小?内核源码流程命令查看总结 tcp_abort_on_overflow 英文翻译理解:溢出中止 所以,溢出指的是什么溢出? Linux中会维护socket全连接队列,所…...

jupyter notebook设置代码提示方法
在命令行运行以下代码: pip install jupyter_contrib_nbextensionsjupyter contrib nbextension install --userpip install jupyter_nbextensions_configuratorjupyter nbextensions_configurator enable --user (有时安装第一行后会自动执行第二行&a…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
