刷题DAY24 | LeetCode 77-组合
1 回溯法理论基础
回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。
所以以下讲解中,回溯函数也就是递归函数,指的都是一个函数。
1.1 回溯法的效率
回溯法的性能如何呢,这里要和大家说清楚了,虽然回溯法很难,很不好理解,但是回溯法并不是什么高效的算法。
因为回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,如果想让回溯法高效一些,可以加一些剪枝的操作,但也改不了回溯法就是穷举的本质。
那么既然回溯法并不高效为什么还要用它呢?因为没得选,一些问题能暴力搜出来就不错了,撑死了再剪枝一下,还没有更高效的解法。
1.2 回溯法解决的问题
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
1.3 如何理解回溯法
回溯法解决的问题都可以抽象为树形结构,是的,我指的是所有回溯法的问题都可以抽象为树形结构!因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,都构成的树的深度。
递归就要有终止条件,所以必然是一棵高度有限的树(N叉树)。
1.4 回溯法模板
在讲二叉树的递归 (opens new window)中我们说了递归三部曲,这里我再给大家列出回溯三部曲。
- 回溯函数模板返回值以及参数
习惯是函数起名字为backtracking,回溯算法中函数返回值一般为void。
再来看一下参数,因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来,所以一般是先写逻辑,然后需要什么参数,就填什么参数。
回溯函数伪代码如下:
void backtracking(参数)
- 回溯函数终止条件
既然是树形结构,那么我们在讲解二叉树的递归 (opens new window)的时候,就知道遍历树形结构一定要有终止条件。所以回溯也有要终止条件。
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
所以回溯函数终止条件伪代码如下:
if (终止条件) {存放结果;return;
}
- 回溯搜索的遍历过程
在上面我们提到了,回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。
集合大小和孩子的数量是相等的!
回溯函数遍历过程伪代码如下:
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果
}
for循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个for循环就执行多少次。
backtracking这里自己调用自己,实现递归。
大家可以从图中看出for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了。
分析完过程,回溯算法模板框架如下:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}
1.5 总结
本篇我们讲解了,什么是回溯算法,知道了回溯和递归是相辅相成的。
接着提到了回溯法的效率,回溯法其实就是暴力查找,并不是什么高效的算法。
然后列出了回溯法可以解决几类问题,可以看出每一类问题都不简单。
最后我们讲到回溯法解决的问题都可以抽象为树形结构(N叉树),并给出了回溯法的模板。
77 组合(medium)
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
思路:
本题是回溯法的经典题目。把组合问题抽象为如下树形结构:
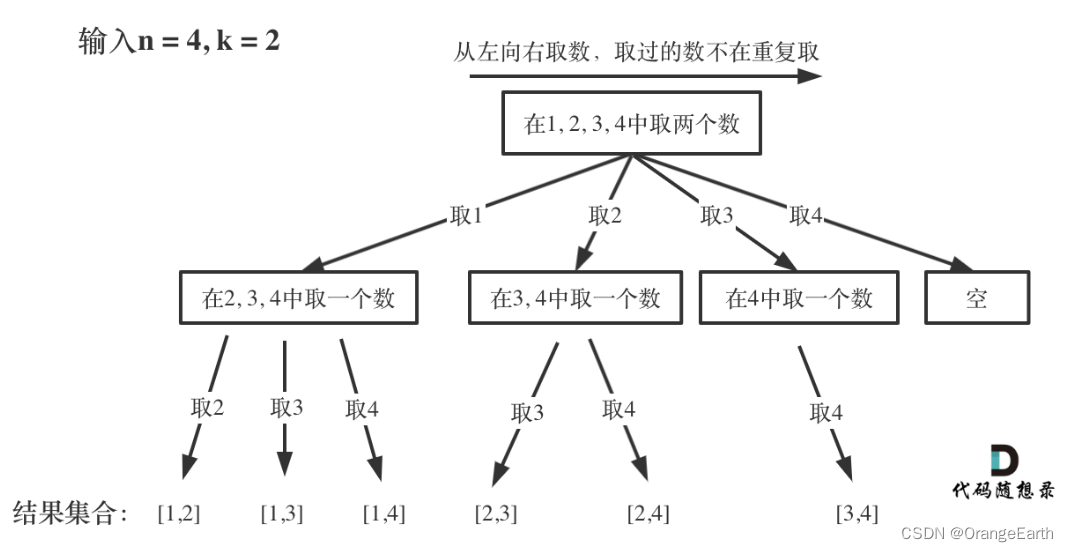
可以看出这棵树,一开始集合是 1,2,3,4, 从左向右取数,取过的数,不再重复取。
第一次取1,集合变为2,3,4 ,因为k为2,我们只需要再取一个数就可以了,分别取2,3,4,得到集合[1,2] [1,3] [1,4],以此类推。
每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围。
图中可以发现n相当于树的宽度,k相当于树的深度。那么如何在这个树上遍历,然后收集到我们要的结果集呢?
图中每次搜索到了叶子节点,我们就找到了一个结果。
相当于只需要把达到叶子节点的结果收集起来,就可以求得 n个数中k个数的组合集合。
回溯法三部曲
- 递归函数的返回值以及参数
在这里要定义两个全局变量,一个用来存放符合条件单一结果,一个用来存放符合条件结果的集合。
代码如下:
vector<vector<int>> result; // 存放符合条件结果的集合
vector<int> path; // 用来存放符合条件结果
其实不定义这两个全局变量也是可以的,把这两个变量放进递归函数的参数里,但函数里参数太多影响可读性,所以我定义全局变量了。
函数里一定有两个参数,既然是集合n里面取k个数,那么n和k是两个int型的参数。
然后还需要一个参数,为int型变量startIndex,这个参数用来记录本层递归的中,集合从哪里开始遍历(集合就是[1,…,n] )。
为什么要有这个startIndex呢?startIndex 就是防止出现重复的组合。
从下图中红线部分可以看出,在集合[1,2,3,4]取1之后,下一层递归,就要在[2,3,4]中取数了,那么下一层递归如何知道从[2,3,4]中取数呢,靠的就是startIndex。
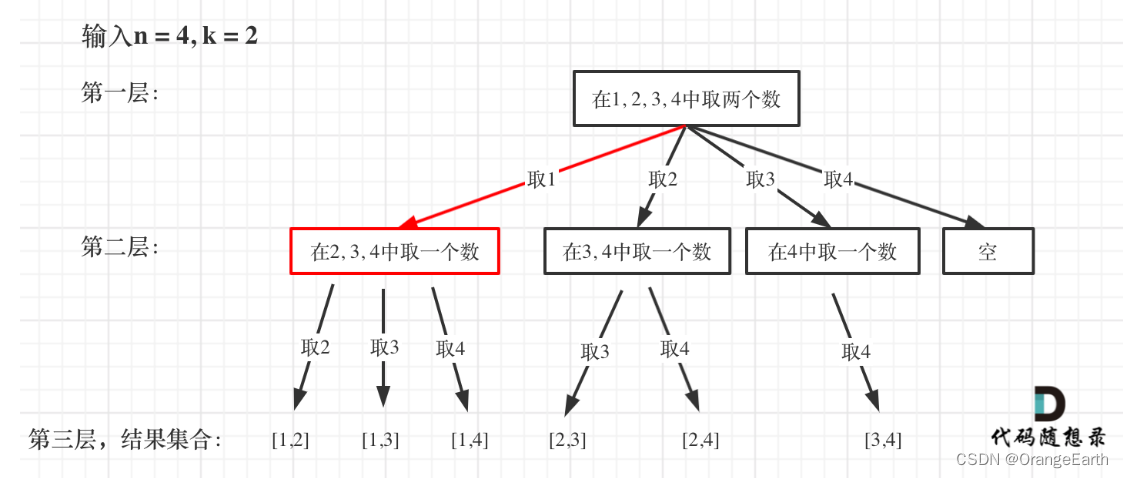
所以需要startIndex来记录下一层递归,搜索的起始位置。
那么整体代码如下:
vector<vector<int>> result; // 存放符合条件结果的集合
vector<int> path; // 用来存放符合条件单一结果
void backtracking(int n, int k, int startIndex)
- 回溯函数终止条件
什么时候到达所谓的叶子节点了呢?
path这个数组的大小如果达到k,说明我们找到了一个子集大小为k的组合了,在图中path存的就是根节点到叶子节点的路径。此时用result二维数组,把path保存起来,并终止本层递归。
所以终止条件代码如下:
if (path.size() == k) {result.push_back(path);return;
}
- 单层搜索的过程
回溯法的搜索过程就是一个树型结构的遍历过程,for循环用来横向遍历,递归的过程是纵向遍历。
for循环每次从startIndex开始遍历,然后用path保存取到的节点i。
代码如下:
for (int i = startIndex; i <= n; i++) { // 控制树的横向遍历path.push_back(i); // 处理节点backtracking(n, k, i + 1); // 递归:控制树的纵向遍历,注意下一层搜索要从i+1开始path.pop_back(); // 回溯,撤销处理的节点
}
可以看出backtracking(递归函数)通过不断调用自己一直往深处遍历,总会遇到叶子节点,遇到了叶子节点就要返回。
backtracking的下面部分就是回溯的操作了,撤销本次处理的结果。
剪枝优化
我们说过,回溯法虽然是暴力搜索,但也有时候可以有点剪枝优化一下的。
在遍历的过程中有如下代码:
for (int i = startIndex; i <= n; i++) {path.push_back(i);backtracking(n, k, i + 1);path.pop_back();
}
这个遍历的范围是可以剪枝优化的,怎么优化呢?
来举一个例子,n = 4,k = 4的话,那么第一层for循环的时候,从元素2开始的遍历都没有意义了。 在第二层for循环,从元素3开始的遍历都没有意义了。
这么说有点抽象,如图所示:
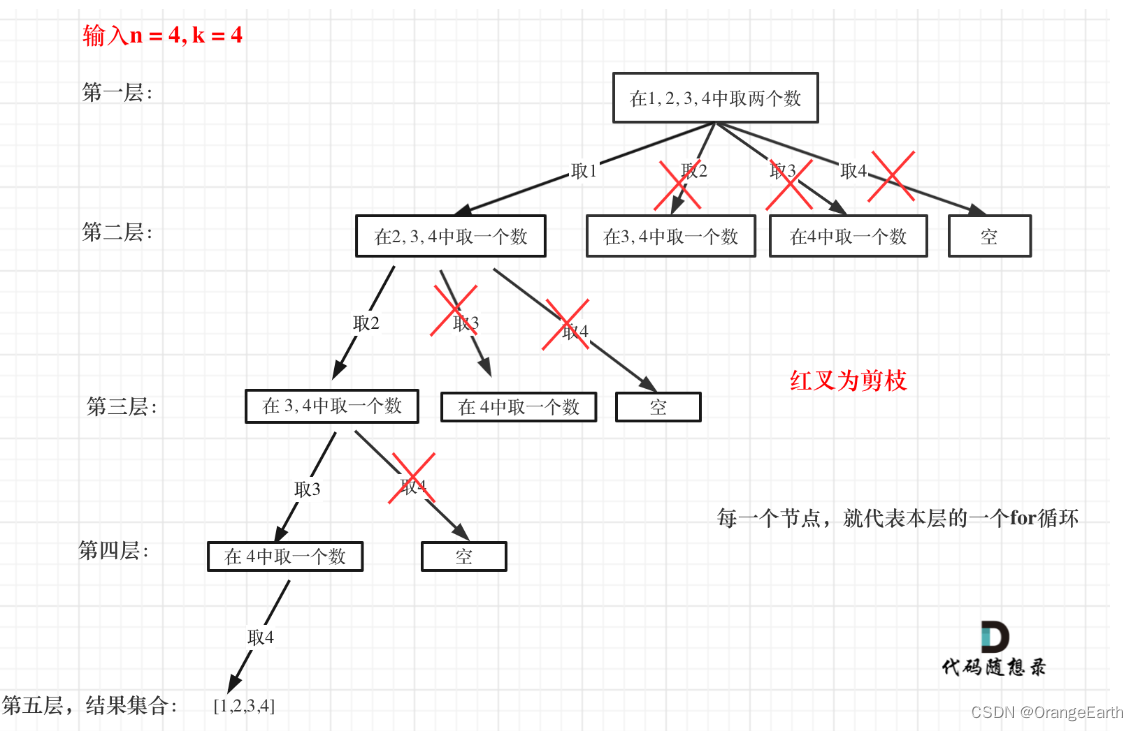
图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。所以,可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。
如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了。
注意代码中i,就是for循环里选择的起始位置。
for (int i = startIndex; i <= n; i++) {
接下来看一下优化过程如下:
-
已经选择的元素个数:path.size();
-
还需要的元素个数为: k - path.size();
-
在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
所以优化之后的for循环是:
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
代码实现1:
class Solution {
private:vector<vector<int>> result; // 存放符合条件结果的集合vector<int> path; // 用来存放符合条件结果void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.push_back(path);return;}for (int i = startIndex; i <= n; i++) {path.push_back(i); // 处理节点backtracking(n, k, i + 1); // 递归path.pop_back(); // 回溯,撤销处理的节点}}
public:vector<vector<int>> combine(int n, int k) {result.clear(); // 可以不写path.clear(); // 可以不写backtracking(n, k, 1);return result;}
};
代码实现2(剪枝):
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.push_back(path);return;}for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 优化的地方path.push_back(i); // 处理节点backtracking(n, k, i + 1);path.pop_back(); // 回溯,撤销处理的节点}}
public:vector<vector<int>> combine(int n, int k) {backtracking(n, k, 1);return result;}
};
详细解析:
思路视频1
思路视频2
代码实现文章
相关文章:

刷题DAY24 | LeetCode 77-组合
1 回溯法理论基础 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。 所以以下讲解中,回溯函数也就是递归函数,指的都是一个函数。 1.1 回溯法的效率 回溯法的性能如何呢࿰…...

Spring Boot为什么默认使用CGLIB动态代理
兼容性: 1. CGLIB 动态代理可以代理任何类型的目标类,无论它是否实现了接口;[注意的是,类被 final 修饰,那么该不可被继承,即不可被代理;同样,类中 final 修饰的方法&am…...

算法详解——Dijkstra算法
Dijkstra算法的目的是寻找单起点最短路径,其策略是贪心加非负加权队列 一、单起点最短路径问题 单起点最短路径问题:给定一个加权连通图中的特定起点,目标是找出从该起点到图中所有其他顶点的最短路径集合。需要明确的是,这里关心…...

利用GANs进行图像生成
生成对抗网络(GANs)是一种深度学习模型,由两部分组成:生成器(Generator)和判别器(Discriminator)。它们通过相互竞争来提高生成器生成高质量图像的能力。以下是如何利用GANs进行图像…...

Flutter-底部弹出框(Widget层级)
需求 支持底部弹出对话框。支持手势滑动关闭。支持在widget中嵌入引用。支持底部弹出框弹出后不影响其他操作。支持弹出框中内容固定头部和下面列表时,支持触摸头部并在列表不在头部的时候支持滑动关闭 简述 通过上面的需求可知,就是在界面中可以支持…...

聚焦两会:数字化再加速,VR全景助力制造业转型
近年来,随着信息技术、人工智能、VR虚拟现实等新兴技术的不断涌现,数字化正日益成为推动当今经济发展的新驱动力。在不久前的两会上,数字化经济和创新技术再度成为热门话题: 国务院总理李强作政府工作报告: 要深入推…...
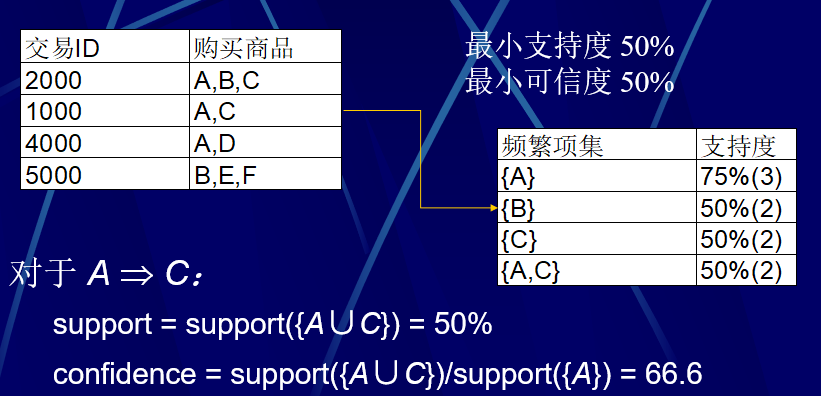
数据挖掘之关联规则
“啤酒和尿布的荣誉” 概念 项 item:单个的事物个体 ,I{i1,i2…im}是所有项的集合,|I|m是项的总数项集(item set)/模式(pattern):项的集合,包含k个项的项集称为k-项集数据集(data set)/数据库…...

java:java.util.BitSet对象的Jackson序列化和反序列化实现
java.util.BitSet是个非常方便的比特位数据存储和操作类,一个 bit 具有2个值:0和1,正好可以用来表示 false 和 true,适用于判断“数据是否存在”的场景。 但是,这个从JDK1.0版本就存在的类,Jackson,Fastjso…...

Go语言学习01-基本程序结构
文章目录 Go语言学习01-基本程序结构基本程序结构应用程序入口退出返回值编写测试程序快速设置连续值基本数据类型类型的预定义值指针类型运算符算数运算符比较运算符用 比较数组 逻辑运算符位运算符&^ 按位 置零 Go语言学习01-基本程序结构 基本程序结构 package main …...
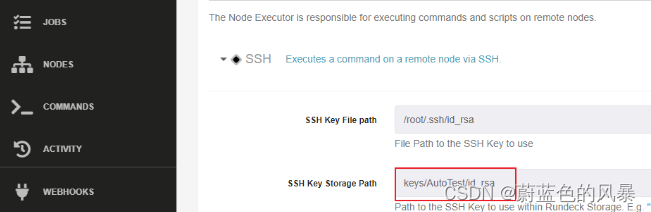
rundeck k8s部署踩坑
1、镜像启动后原来的定时任务无法运行 参考: https://github.com/rundeck/rundeck/issues/4275 https://stackoverflow.com/questions/60942785/env-variable-for-rundeck-feature-joblifecycleplugin-enabled/60959605#60959605 结论: (1&…...
架构设计类)
每天学习几道面试题|Kafka(二)架构设计类
文章目录 1. Kafka 是如何保证高可用性和容错性的?2. Kafka 的存储机制是怎样的?它是如何处理大量数据的?3. Kafka 如何处理消费者的消费速率低于生产者的生产速率?4. Kafka 集群中的 Controller 是什么?它的作用是什么…...

Spring 实现 OAuth2 授权之解决方案
Spring Security OAuth2 - 已经废弃的项目 早期的Spring 使用 Spring Security OAuth2 实现 OAuth 2.0 的认证服务器和资源服务器。OAuth2是一个授权框架,它允许第三方应用获取有限的访问权限,而无需获取用户的账号和密码等敏感信息。通过这种方式,OAuth2协议实现了安全的用…...
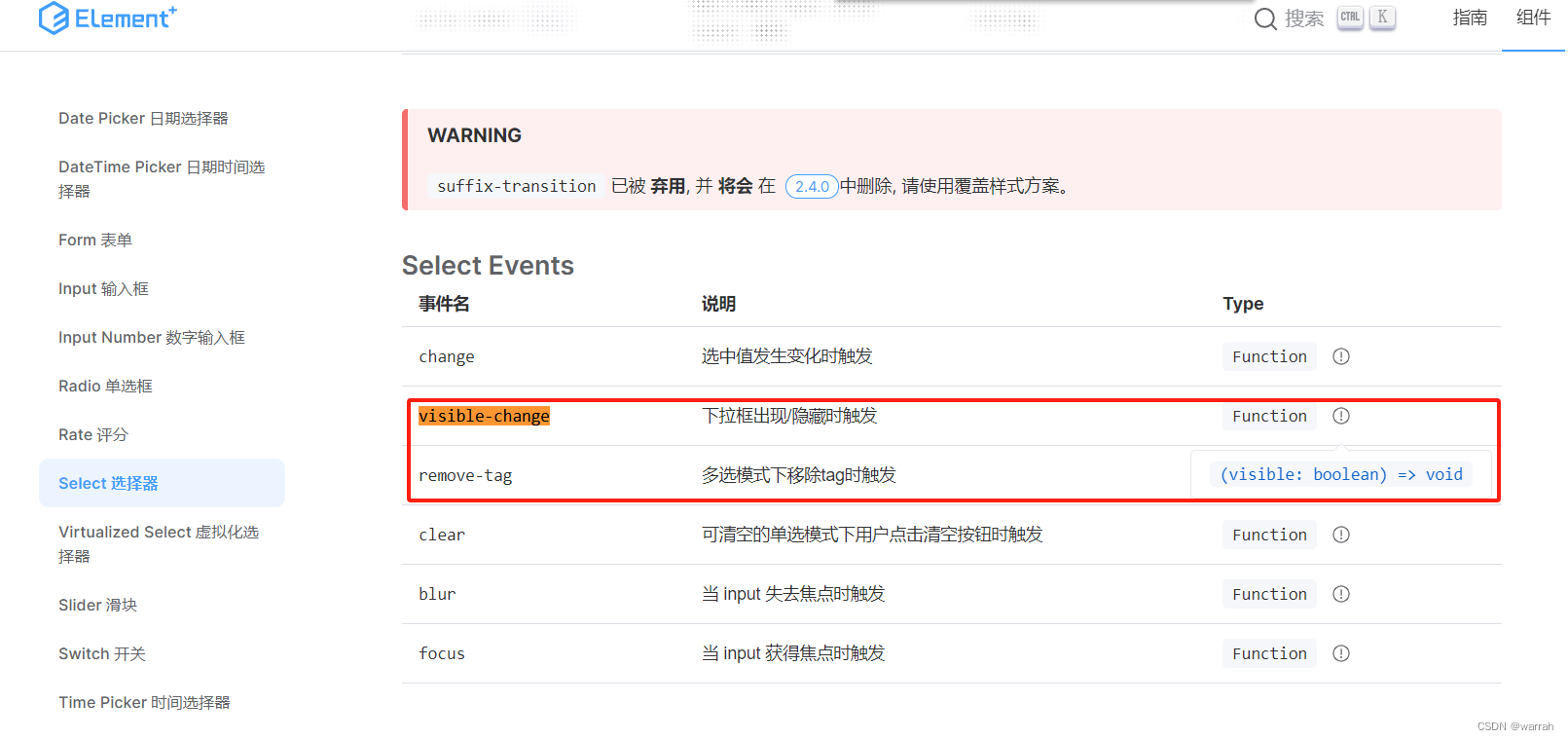
el-select使用filterable下拉无法关闭得问题
这里推荐一个前端框架 sakuya / SCUI,他里面有个formTable,可以解决很多订单明细保存得问题。基本沿用element-plus的前端使用模式,让表单表格变的非常容易。 这个的供应商插件,当使用filterable后,点击表格重的选项&…...

基于javaweb(springboot)城市地名地址信息管理系统设计和实现
基于javaweb(springboot)城市地名地址信息管理系统设计和实现 博主介绍:多年java开发经验,专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 央顺技术团队 Java毕设项目精品实战案例《1000套》 欢迎点赞 收藏 ⭐留言…...
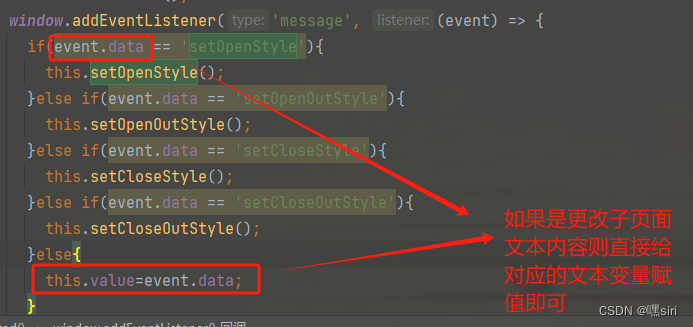
vue iframe实现父页面实时调用子页面方法和内容
父页面标签添加鼠标按下事件 父页方法中建立iframe通信 实时调用子页面方法 实时更改子页面文本内容...
HarmonyOS ArkTS 开发基础/语言
目录 一、ArkUI (方舟开发框架) 概述 1.1 基本概念 1.2 两种开发范式 1.3 不同应用类型支持的开发范式 二、ArkTS 声明式开发范式 2.1 开发能力 2.2 整体架构 三、ArkTS 基础类型 3.1 Any 类型 3.2 数字类型 3.3 字符串类型 3.4 布尔类型 3.5 联合类型 3.6 数组类…...

AI大模型学习
AI大模型学习 在当前技术环境下,AI大模型学习不仅要求研究者具备深厚的数学基础和编程能力,还需要对特定领域的业务场景有深入的了解。通过不断优化模型结构和算法,AI大模型学习能够不断提升模型的准确性和效率,为人类生活和工作…...
2024年【T电梯修理】考试内容及T电梯修理作业考试题库
题库来源:安全生产模拟考试一点通公众号小程序 T电梯修理考试内容根据新T电梯修理考试大纲要求,安全生产模拟考试一点通将T电梯修理模拟考试试题进行汇编,组成一套T电梯修理全真模拟考试试题,学员可通过T电梯修理作业考试题库全真…...
2.vscode 配置python开发环境
vscode用着习惯了,也不想再装别的ide 1.安装vscode 这一步默认已完成 2.安装插件 搜索插件安装 3.选择调试器 Ctrl Shift P(或F1),在打开的输入框中输入 Python: Select Interpreter 搜索,选择 Python 解析器 选择自己安…...

[蓝桥杯 2015 省 B] 生命之树
题目链接 [蓝桥杯 2015 省 B] 生命之树 题目描述 在 X 森林里,上帝创建了生命之树。 他给每棵树的每个节点(叶子也称为一个节点)上,都标了一个整数,代表这个点的和谐值。 上帝要在这棵树内选出一个节点集合 S S S&…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
