二叉树试题解析
一、单项选择题
01.下列关于二叉树的说法中,正确的是( C ).
A.度为2的有序树就是二叉树
B.含有n个结点的二叉树的高度为
C.在完全二叉树中,若一个结点没有左孩子,则它必是叶结点
D.含有n个结点的完全二叉树的高度为
解析:A 二叉树中,若某结点只有一个孩子,则这个孩子的左右次序是确定的,而在度为2 的有序树中,若某节点只有一个孩子,则这个孩子就无需区分其左右次序
B仅当是完全二叉树时才有意义,对于任意一颗二叉树,高度可能为~n
C在完全二叉树中,若有度为1的结点,则只可能有一个,且该结点只有左孩子而没有右孩子
D完全二叉树的高度为或
02.“二叉树为空”意味着二叉树( C ).
A.根结点没有子树 B.不存在
C.没有结点 D.由一些没有赋值的空结点构成
03.以下说法中,正确的是( A)。
A.在完全二叉树中,叶结点的双亲的左兄弟(若存在)一定不是叶结点
B.任何一棵二叉树中,叶结点数为度为2的结点数减1,即n0=n2-1
C.完全二叉树不适合顺序存储结构,只有满二叉树适合顺序存储结构
D.结点按完全二叉树层序编号的二叉树中,第i个结点的左孩子的编号为2i
解析:在完全二叉树中,叶结点的双亲的左兄弟的孩子一定在其前面(且一定存在),所以双亲的左兄弟(若存在)一定不是叶结点,选项A正确。n应等于n2+ 1,选项B错误。完全二叉树和满二叉树均可以采用顺序存储结构,选项C错误。第i个结点的左孩子不一定存在,选项D错误。
04.具有10个叶结点的二叉树中有( B )个度为2的结点。
A.8 B.9 C. 10 D.11
解析:由二叉树的性质n0=n2+1,得n2=n0-1=10-1=9
05.设高度为h的二叉树上只有度为0和度为2的结点,则此类二叉树中所包含的结点数至
少为( B ).
A. h B.2h-1 C. 2h+1 D.h+1
解析:结点最少的情况如下图所示。除根结点层只有1个结点外,其他h-1层均有两个结点,点总数=2(h-1)+1= 2h-1。
06.具有n个结点且高度为n的二叉树的数目为( D )。
A.logn B.n/2 C. n D.2n-1
解析:除根结点外,在其余n -1个结点中,每个结点要么是其父结点的左孩子,要么是其父结点的右孩子,每个结点都有两种可能,n-1个结点共有2^n-1种不同的组合形态。
07.假设一棵二叉树的结点个数为50,则它的最小高度是(C).
A.4 B.5 C. 6 D.7
解析:第一层1个,第二层2个,第三层4个,第四层8个,第五层16个,第六层50-31=19个
08.设二叉树有2n个结点,且m<n,则不可能存在(C)的结点。
A. n个度为0 B.2m个度为0 C. 2m个度为1 D. 2m个度为2
解析:由二叉树的性质1可知n0=n2+1,结点总数=2n=n0+n1+n2=n1+2n2+1,则n1=2(n-n2)-1,所以n1为奇数,说明该二叉树中不可能有2m个度为1的结点
09.一个具有1025个结点的二叉树的高h为( C )。
A.11 B.10 C.11 ~1025 D.10~1024
解析:j当二叉树为单支树时具有最大高度,即每层上只有一个结点,最大高度为1025。而当树为完全二叉树时,其高度最小,最小高度为log2n+1= 11。
10.设二叉树只有度为0和2的结点,其结点个数为15,则该二叉树的最大深度为( C )
A.4 B.5 C.8 D.9
解析:最大深度即第一层有一个结点,其余h-1层都有2个结点,结点总数=1+2(h-1)=15,h=8
11.高度为h的完全二叉树最少有( C )个结点。
A.2^h B.2^h+1 C. 2^(h-1) D.2^h-1
12.已知一棵完全二叉树的第6层(设根为第1层)有8个叶结点,则完全二叉树的结点
数最少是( A )。
A.39 B.52 C.111 D.119
解析:第6层有叶结点说明完全二叉树的高度可能为6或7,显然树的高度为6时结点最少,若第六层有8个叶结点,则前面5层为满二叉树,所以完全二叉树的结点个数最少为2^5-1+8=39个结点
13.若一棵深度为6的完全二叉树的第6层有3个叶结点,则该二叉树共有( A )个叶结点
A.17 B.18 C. 19 D.20
解析:第五层共有2^4=16个结点,第六层的3个叶结点对应第五层最左边的两个结点,所以第五层剩下的14个结点都是叶结点,加上第六层的3个一共17个叶结点
14.一棵完全二叉树上有1001个结点,其中叶结点的个数是( D )。
A.250 B.500 C. 254 D.501
解析:完全二叉树叶子结点>1001/2
15.若一棵二叉树有126个结点,在第7层(根结点在第1层)至多有( C )个结点。
A.32 B.64 C. 63 D、不存在第7层
解析:第七层最多2^6-1 = 63个结点,七层满二叉树共2^7-1=127个结点 所以第七层只少一个结点
16.一棵有124个叶结点的完全二叉树,最多有( B )个结点。
A.247 B.248 C.249 D.250
解析:非空二叉树度为0和2的结点数关系n0=n2+1,n2=123,总结点数n=n0+n1+n2=124+n1+123,根据完全二叉树的特性,n1等于0或1,n1=1时结点最多,所以最多248个结点
17.一棵有n个结点的二叉树采用二叉链存储结点,其中空指针数为( B )。
A. n B.n+1 C. n-1 D. 2n
解析:树中1个指针对应1个分支,n个结点的树共n-1个分支,即n-1个非空指针,每个结点都有两个指针域,所以空指针的个数为2n-(n-1)=n+1
18.设有n(n≥1)个结点的二叉树采用三叉链表表示,其中每个结点包含三个指针,分别
指向其左孩子、右孩子及双亲(若不存在,则置为空),则下列说法中正确的是 ( A )
Ⅰ树中空指针的数量为n+2
Ⅱ.所有度为2的结点均被三个指针指向
Ⅲ每个叶结点均被一个指针所指向
A. I B. I、Ⅱ C.I、Ⅲ D.II、Ⅲ
解析:二叉链表表示的二叉树空指针数量为n+1,三叉链表表示的二叉树多了一个根节点指向双亲的空指针,所以树中空指针的数量为n+2,Ⅰ正确。若根结点的度为2,则只有左右两个孩子指向它,Ⅱ错,若整棵树只有一个根结点,则没有指针指向它,Ⅲ错
19.在一棵完全二叉树中,其根的序号为1,( A ) 可判定序号为p和q的两个结点是否在同一层。![]()
 20.在一个用数组表示的完全二叉树中,根结点的下标为[i/2],那么下标为17和19的结点的最近公共祖先的下标是( C ).
20.在一个用数组表示的完全二叉树中,根结点的下标为[i/2],那么下标为17和19的结点的最近公共祖先的下标是( C ).
A.1 B.2 C.4 D.8
解析:下标为17的祖先有8、4、2、1。下标为19的祖先有9、4、2、1,最近的为4
21.假定一棵三叉树的结点数为50,则它的最小高度为( C ).
A.3 B.4 C.5 D. 6
解析:假设满足条件的是一颗完全三叉树,这棵树第i层最多3^(i-1)个结点。第一层1个,第二层3个,第三层9个,第四层27个,总结点为50,第五层10个
22.具有n个结点的三叉树用三叉链表表示,则树中空指针域的个数为( B )
A. 3n+ 1 B.2n+1 C.3n - 1 D. 3n
解析:三叉树用三叉链表表示,每个结点均有3个指针域指向3个孩子,共有3n个指针域,n个结点构成的一棵树只需要n-1个指针,所以空指针域=3n-(n-1)=2n+1
23.对于一棵满二叉树,共有n个结点和m个叶结点,高度为h,则( D )
A. n=h+m B. n+m=2h C. m=h-1 D. n=2^h-1
解析:高度为h的二叉树总结点树n=2^0+2^1+...+2^(h-1),m=2^(h-1)
24.【2009统考真题】已知一棵完全二叉树的第6层(设根为第1层)有8个叶结点,则该
完全二叉树的结点个数最多是( C ).
A. 39 B.52 C.111 D.119
解析:完全二叉树的叶结点在最后两层,第六层8个叶结点,最多情况下第七层也有叶结点,缺少第六层的16个叶节点,结点个数最多为2^7-1-2*8=111
25.【2011统考真题】若一棵完全二叉树有768个结点,则该二叉树中叶结点的个数是( C )
A.257 B.258 C.384 D.385
解析:最后一个分支结点的编号为[768/2]=384,所以叶结点的个数为768-384
26.【2018统考真题】设一棵非空完全二叉树T的所有叶结点均位于同一层,且每个非叶结
点都有2个子结点。若T有k个叶结点,则T的结点总数是( A )。
A.2k-1 B.2k C.R D.2^k-1
解析:每个叶结点都有两个子结点,说明结点个数为奇数
27.【2020统考真题】对于任意一棵高度为5且有10个结点的二叉树,若采用顺序存储结构保存,每个结点占1个存储单元(仅存放结点的数据信息),则存放该二叉树需要的存储单元数量至少是(A)。
A.31 B.16 C.15 D. 10
解析:二叉树用顺序存储时需要用数组来表示结点间的父子关系,所以高度为5的二叉树,前五层的结点都要存起来,需要存储的数量为1+2+4+8+16=31,或2^5-1
28.【2022统考真题】若三叉树T中有244个结点(叶结点的高度为1),则T的高度至少是( C )。
A.8 B.7 C. 6 D.5
解析:高度为5的满三叉树的结点个数为1+3+9+27+81=121,所以至少要6层
相关文章:

二叉树试题解析
一、单项选择题 01.下列关于二叉树的说法中,正确的是( C ). A.度为2的有序树就是二叉树 B.含有n个结点的二叉树的高度为 C.在完全二叉树中,若一个结点没有左孩子,则它必是叶结点 D.含有n个结点的完全二叉树的高度为解析:A 二叉树…...

计算机服务器中了faust勒索病毒怎么办,faust勒索病毒解密工具流程
网络是一把利剑,可以方便企业开展各项工作业务,为企业提供极大的便利,但随着网络技术的不断发展与应用,网络数据安全威胁也在不断增加,给企业的正常生产运营带来了极大困扰,近日,云天数据恢复中…...

初次部署麒麟V10系统需要的配置,快速完成测试环境的搭建
配置麒麟V10 设置“root”登录密码 sudo su -passwd # 设置登录密码允许“root”远程登录 sudo vim /etc/ssh/sshd_configsshd_config # ↓↓↓↓修改的内容↓↓↓↓ PermitRootLogin yes # ↑↑↑↑修改的内容↑↑↑↑重启服务 sudo systemctl restart sshd允许通过图像界…...

DOcker in Docker 原理与实战代码详解
Docker in Docker(DinD)指的是在Docker容器内部运行另一个Docker守护进程和客户端。这种技术可以用于创建嵌套的Docker环境,例如在持续集成/持续部署(CI/CD)管道中构建和测试Docker镜像。然而,需要注意的是…...

公司系统中了.rmallox勒索病毒如何恢复数据?
早晨上班时刻: 当阳光逐渐洒满大地,城市的喧嚣开始涌动,某公司的员工们纷纷踏入办公大楼,准备开始新的一天的工作。他们像往常一样打开电脑,准备接收邮件、查看日程、浏览项目进展。 病毒悄然发作: 就在员…...
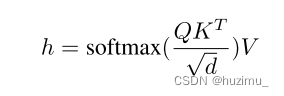
论文阅读:Forget-Me-Not: Learning to Forget in Text-to-Image Diffusion Models
Forget-Me-Not: Learning to Forget in Text-to-Image Diffusion Models 论文链接 代码链接 这篇文章提出了Forget-Me-Not (FMN),用来消除文生图扩散模型中的特定内容。FMN的流程图如下: 可以看到,FMN的损失函数是最小化要消除的概念对应的…...

html5cssjs代码 036 CSS默认值
html5&css&js代码 036 CSS默认值 一、代码二、解释 CSS默认值(也称为浏览器默认样式)是指当HTML元素没有应用任何外部CSS样式时,浏览器自动为这些元素赋予的一组基本样式。这些样式是由浏览器的默认样式表(User Agent sty…...

小米路由器4A千兆版刷回官方固件
原文链接:小米路由器4A千兆版刷回官方固件及修改SN绑定APP-小米无线路由器及小米网络设备-恩山无线论坛 (right.com.cn) 进入breed 由于openwrt工作不稳定,决定重新刷回官方固件。 由于当前路由器已经刷过breed,不再重新刷入。 如何刷入b…...
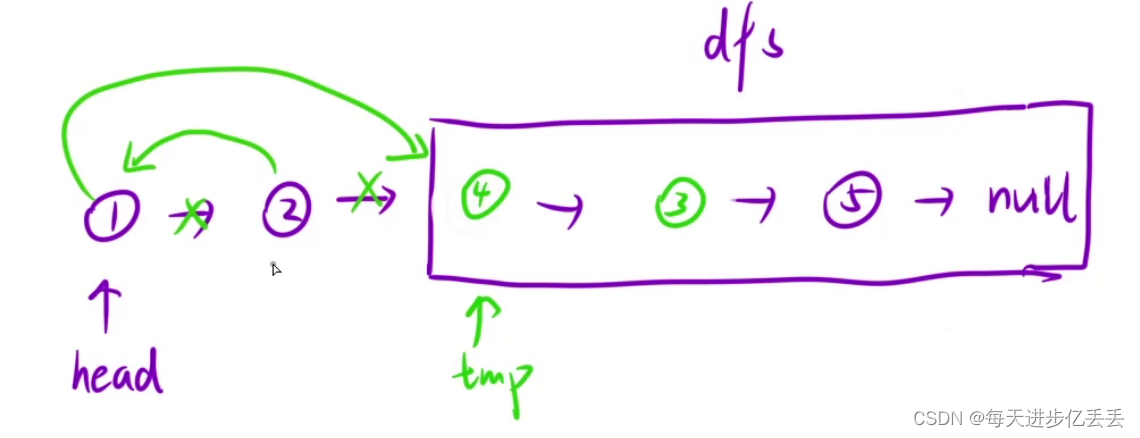
【Leetcode每日一题】 递归 - 两两交换链表中的节点(难度⭐)(38)
1. 题目解析 题目链接:24. 两两交换链表中的节点 这个问题的理解其实相当简单,只需看一下示例,基本就能明白其含义了。 2.算法原理 一、理解递归函数的含义 首先,我们需要明确递归函数的任务:给定一个链表…...
如何部署GPT模型至自有服务器:从零开始搭建你的智能聊天机器人
引言 GPT模型是自然语言处理领域的重要突破,它能够通过生成式的文本生成方式,实现与用户的智能交互。本文将详细介绍如何将GPT模型部署到自有服务器上,并编写一个基本的API接口来实现与聊天机器人的交互。 目录 引言 一、准备工作 首先&am…...
)
uniapp 之 一些常用方法的封装(页面跳转,页面传参等)
util.js 提示:permission.js是uniapp插件市场由官方DCloud_heavensoft提供的App权限判断和提示插件。 import permision from "/js_sdk/wa-permission/permission.js"/*** uni.toast 封装* param {String} msg toast 提示内容* param {Number} duration …...

flutter 单列选择器
引入 flutter_pickers: ^2.1.9 import package:flutter_pickers/pickers.dart; import package:flutter_pickers/style/default_style.dart; import package:flutter_pickers/style/picker_style.dart;List<String> _numberList [99,98,97,96,95,94,93,92,91,90,89,88,…...

管理类联考–复试–英文面试–问题–WhatWhyHow--纯英文汇总版
文章目录 Do you have any hobbies? What are you interested in? What do you usually do in your spare time? Could you tell me something about your family? Could you briefly introduce your family? What is your hometown like? Please tell me so…...
亮数据代理IP轻松解决爬虫数据采集痛点
文章目录 一、爬虫数据采集痛点二、为什么使用代理IP可以解决?2.1 爬虫和代理IP的关系2.2 使用代理IP的好处 一、爬虫数据采集痛点 爬虫数据采集可能会面临一些挑战和痛点,其中包括: 爬虫代码维护难:网站的结构可能会经常变化&am…...
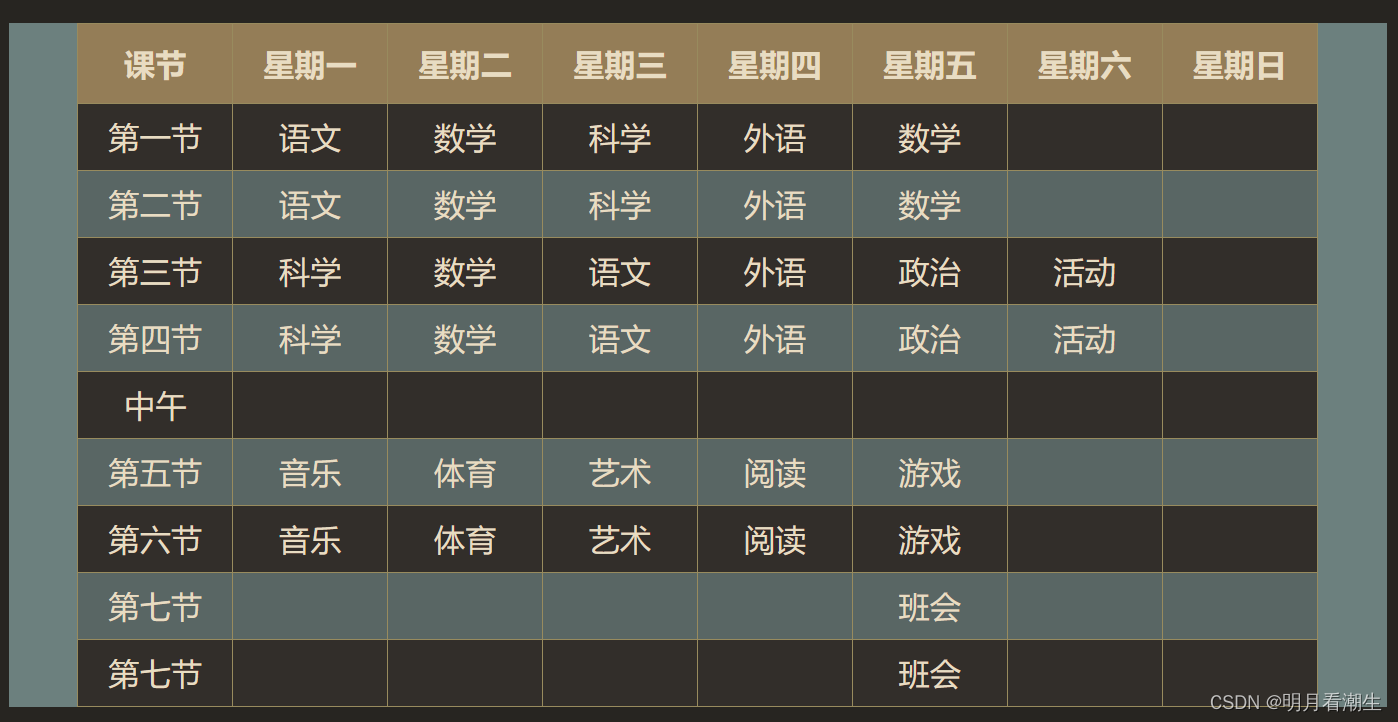
html5cssjs代码 035 课程表
html5&css&js代码 035 课程表 一、代码二、解释基本结构示例代码常用属性样式和装饰响应式表格辅助技术 一个具有亮蓝色背景的网页,其中包含一个样式化的表格用于展示一周课程安排。表格设计了交替行颜色、鼠标悬停效果以及亮色表头,并对单元格设…...
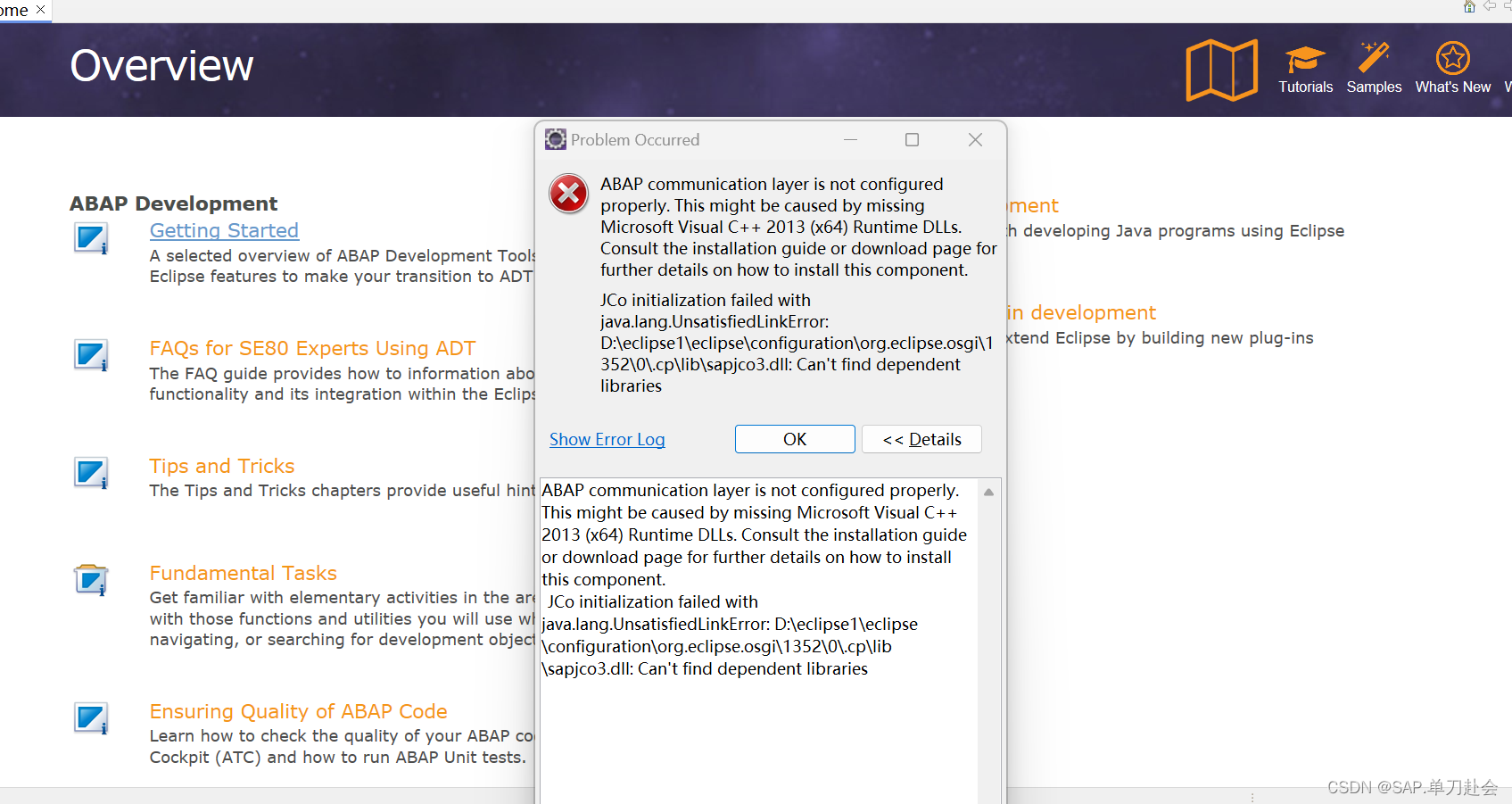
Eclipse For ABAP:安装依赖报错
1.安装好Eclipse后需要添加依赖,这里的地址: https://tools.hana.ondemand.com/latest 全部勾选等待安装结束; 重启后报错:ABAP communication layer is not configured properly. This might be caused by missing Microsoft Visual C++ 2013 (x64) Runtime DLLs. Consu…...

C++特性三:多态---纯析构和纯虚析构
多态使用时,如果子类中有属性开辟到堆区,那么父类指针在释放时无法调用到子类的析构代码 解决方式:将父类中的析构函数改为虚析构或者纯虚析构 虚析构和纯虚析构共性: 1.可以解决父类指针释放子类对象 2.都需要有具体的函数实现…...

创建可引导的 macOS 安装器
你可以将外置驱动器或备用宗卷用作安装 Mac 操作系统的启动磁盘。 以下高级步骤主要适用于系统管理员以及其他熟悉在“终端”中输入命令的经验丰富的用户。 升级 macOS 或重新安装 macOS 不需要可引导安装器,但如果你要在多台电脑上安装 macOS,而又不…...

ssm+vue的公廉租房维保系统(有报告)。Javaee项目,ssm vue前后端分离项目。
演示视频: ssmvue的公廉租房维保系统(有报告)。Javaee项目,ssm vue前后端分离项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构&…...
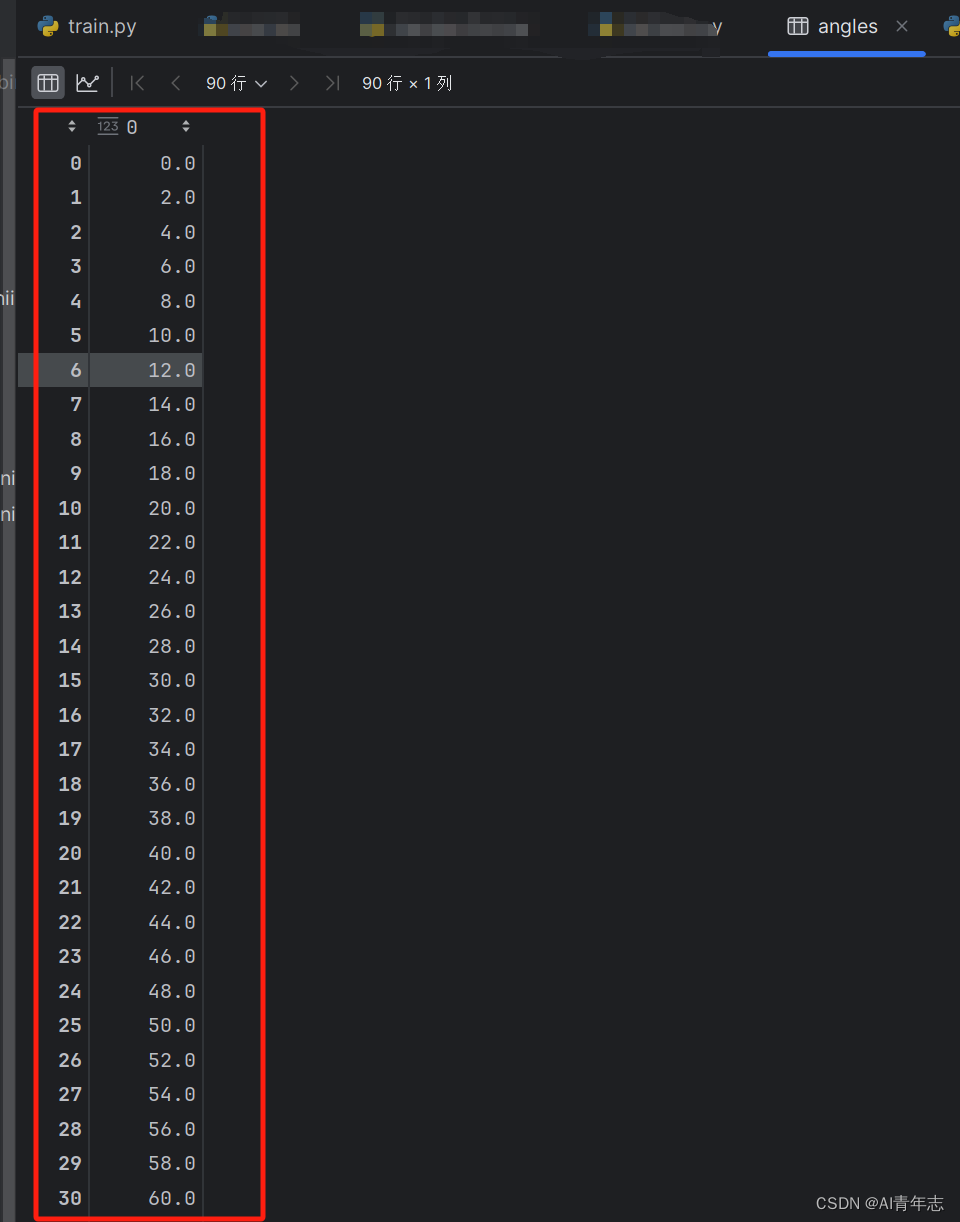
【pycharm】作为Array查看出现数据无法显示问题(已解决)
【pycharm】作为Array查看出现数据无法显示问题(已解决) 当我们在调试代码的时候,需要对某个变量进行查看,就如同在matlab中,我们可以直接在工作区对某个变量进行双击查看矩阵变量的具体数值 在这里我遇到一个问题&am…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
