Transformer的前世今生 day02(神经网络语言模型、词向量)
神经网络语言模型
- 使用神经网络的方法,去完成语言模型的两个问题,下图为两层感知机的神经网络语言模型:
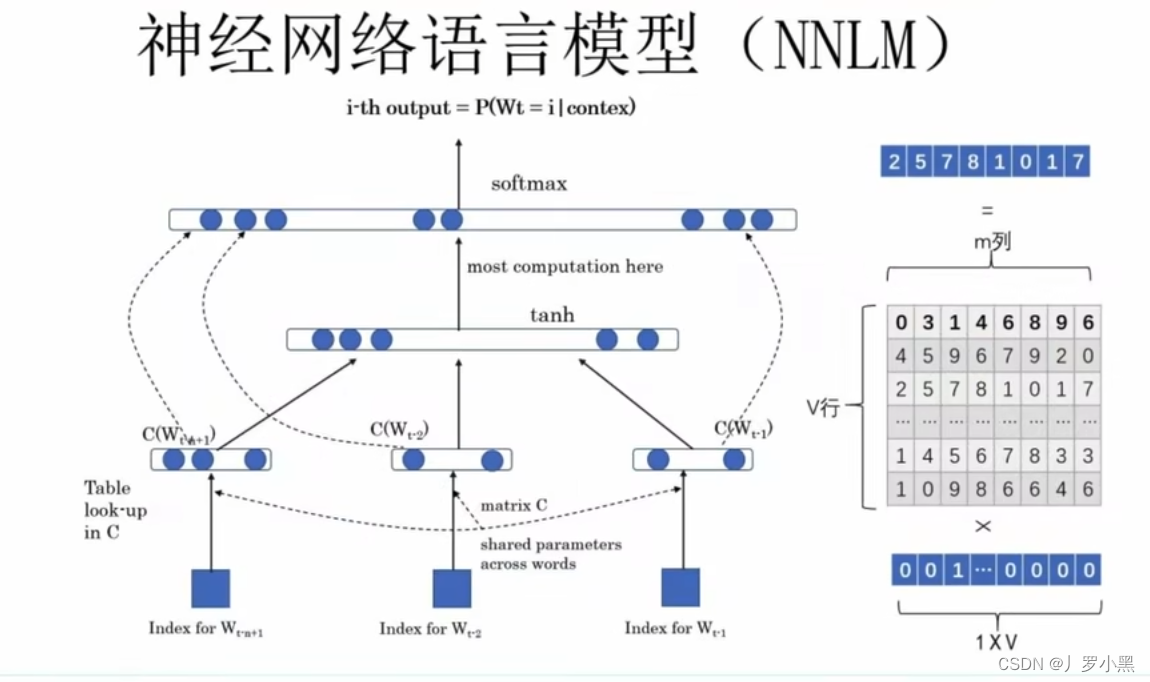
- 假设词典V内有五个词:
“判断”、“这个”、“词”、“的”、“词性”,且要输出P(w_next | “判断”、“这个”、“词”、“的”)的概率,即要解决哪一个词放在这句话后面的概率最大的问题。 - 输入为:W1、W2、W3、W4(前四个单词的独热编码),分别乘随机矩阵,再将结果拼接起来得到C,如下:
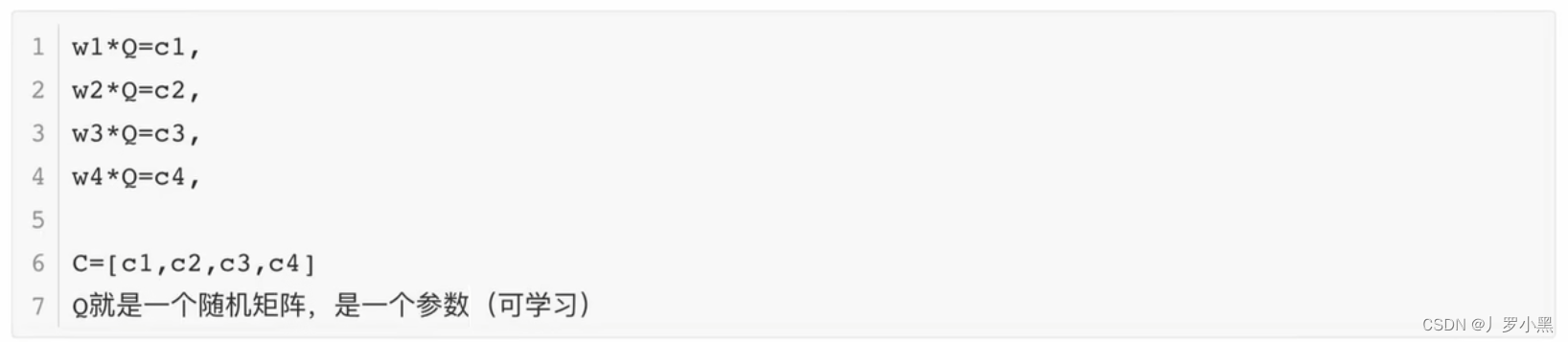
- 再经过两层隐藏层,最后通过一个softmax函数,得到输出结果为词库中所有词,分别填在这个位置的概率。得出最大概率的就是最后一个词“词性”,如下:

词向量
- 用一个向量表示一个单词,独热编码也属于词向量,但是独热编码有两个缺点:尺寸大,不好计算相似度。
- 但是词向量通过随机矩阵Q可以解决这两个缺点。
- 获得词向量的过程如下:

- 假设c1的计算过程如下:
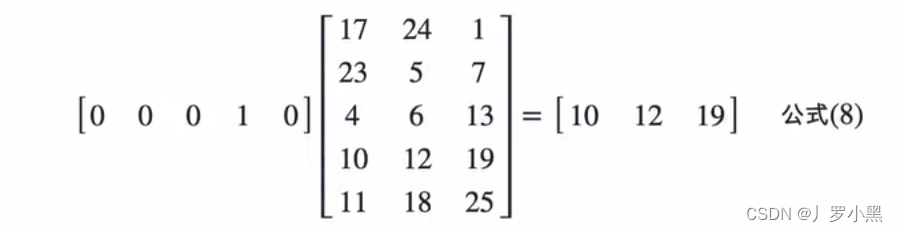
- 由于之前我们拿独热编码来表示单词,但是我们将独热编码乘Q(随机矩阵)得到的一个向量,也可以表示这个单词
- 且由于我们的Q矩阵是一个参数,可以学习,即随着模型训练的越来越好,通过Q得到的向量也就越能准确的代表这个单词。
- 同时我们可以通过矩阵Q来控制输出向量的大小
- 如上图,c1就是“判断”这个词的词向量
- 同时,由于两个词的独热编码之间不好计算相似度(有很多0),如采用余弦相似度,结果也为0。但是我们转换成词向量后,结果不再是0,那么就可以一定程度上描述两个词之间的相似度,例如下图:

以下为预备知识
单层感知机
- 单层感知机是一个线性模型,可以用下图来表示:输入经过全连接层(可以有一层或多层,但是多层线性函数最后可以看作是一层线性函数)得到输出,即Y=Wx+b
- 线性层 / 全连接层 / 稠密层:最好叫他为全连接层,因为有时层内会包含非线性函数
- 假设输入有n个,输出有m个,则w、b、y的个数如下:

多层感知机
- 多层感知机使用了隐藏层和激活函数,是非线性模型
- 隐藏层是对于输出层来说的,只有最后一层全连接层对于输出层是可见的,且最后一层的全连接层一般不带激活函数,所以其他全连接层叫隐藏层
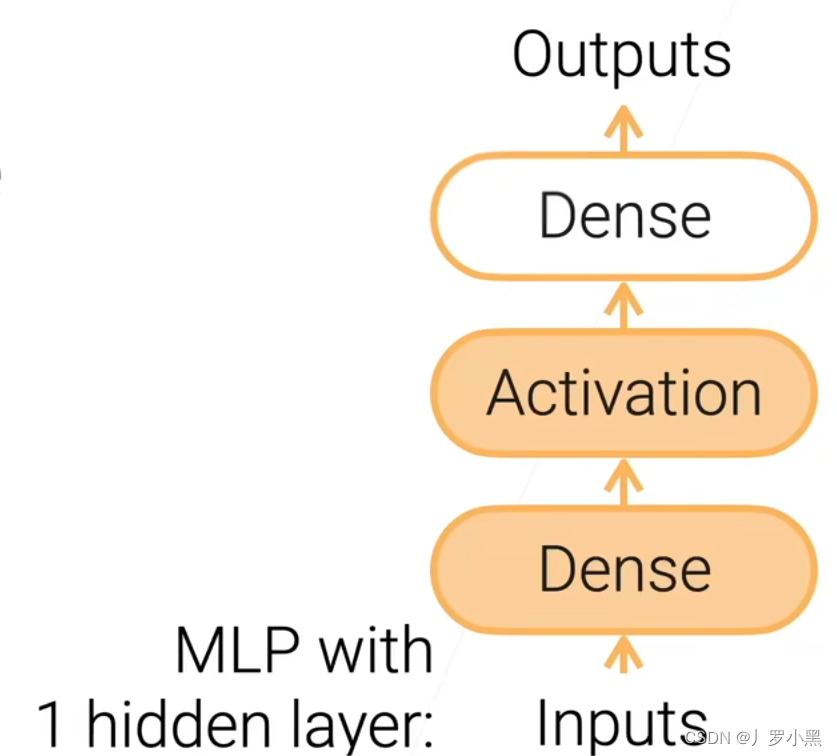
- 激活函数是放在隐藏层中,用来拟合非线性的,常用的激活函数是Sigmoid,Tanh,ReLU,下图为有一层隐藏层的多层感知机:
独热编码
- 目的是让计算机认识单词
- 用矩阵的形式,存储所有单词。且在矩阵中,每一个元素都代表一个单词,这就要求矩阵的行列等于单词数,如下图:
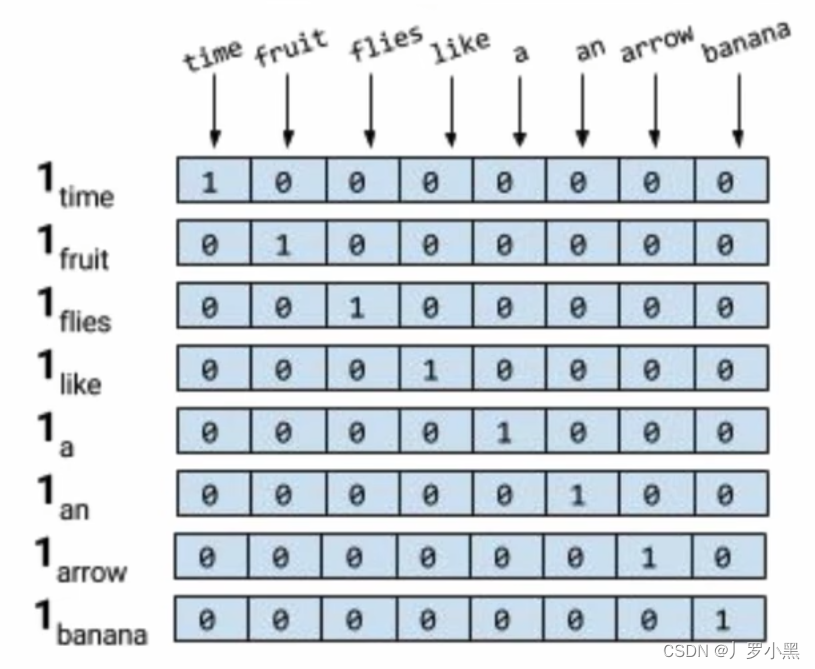
- 独热编码有两个缺点:
- 矩阵的尺寸很容易过大,因为他需要行列等于单词数
- 相似单词之间的独热编码没有任何关联,通常使用余弦相似度来计算文本之间的相似度,但是现实世界中相似单词之间是有关联的
参考文献
- 05 神经网络语言模型(独热编码+词向量的起源)
相关文章:

Transformer的前世今生 day02(神经网络语言模型、词向量)
神经网络语言模型 使用神经网络的方法,去完成语言模型的两个问题,下图为两层感知机的神经网络语言模型: 假设词典V内有五个词:“判断”、“这个”、“词”、“的”、“词性”,且要输出P(w_next | “判断”、“这个”、…...

【Linux】多线程编程基础
💻文章目录 📄前言🌺linux线程基础线程的概念线程的优缺点线程与进程的区别 线程的创建 🌻linux线程冲突概念互斥锁函数介绍加锁的缺点 📓总结 📄前言 无论你是否为程序员,相信多线程这个词汇应…...
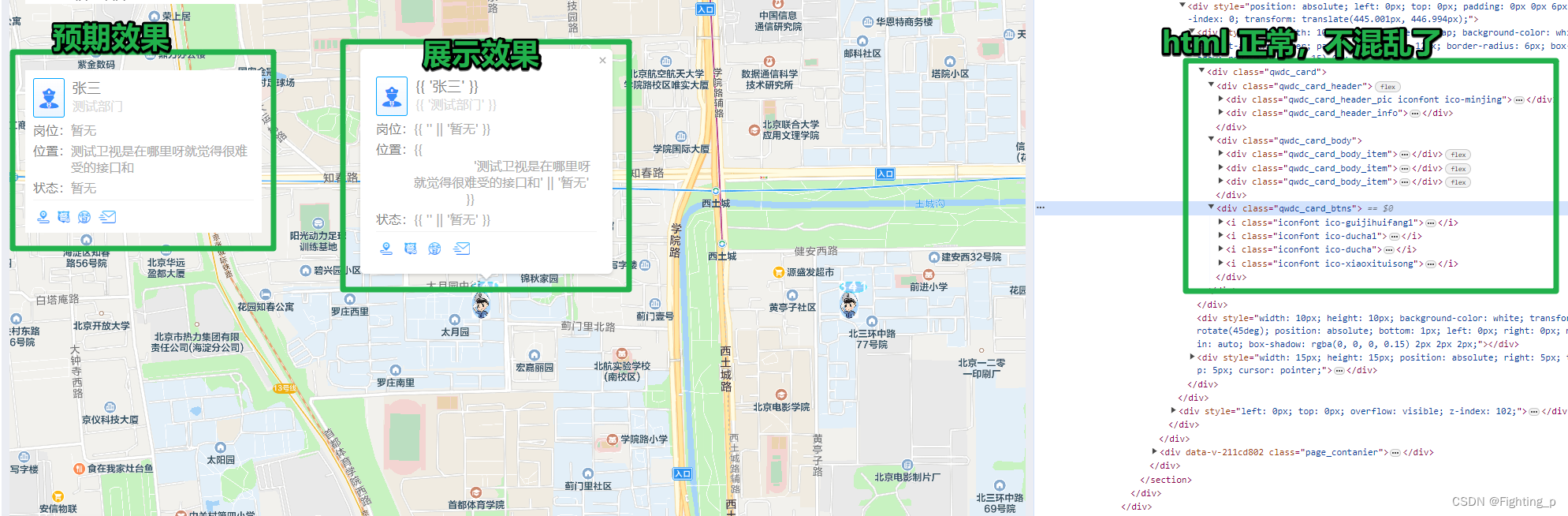
【地图】腾讯地图 - InfoWindow 自定义信息窗口内容时,内容 html 嵌套混乱问题
目录 需求描述问题问题代码页面展示 解决原因解决办法解决代码页面展示 代码汇总注 需求描述 腾讯地图上画点位,点击点位展示弹框信息 问题 问题代码 // 打开弹框 openInfoWindow(position, content) {this.infoWindow new TMap.InfoWindow({map: this.map,posit…...

Vue3、element-plus和Vue2、elementUI的一些转换
插槽 Vue3<template #default"scope"></template> <template #footer></template>Vue2<template slot-scope"scope"></template> <template slot"footer"></template>JS定义 Vue3 <script…...
Go语言gin框架中加载html/css/js等静态资源
Gin框架没有内置静态文件服务,但可以使用gin.Static或gin.StaticFS中间件来提供静态文件服务。 效果图如下: 一、gin 框架加载 Html 模板文件的方法 方式1:加载单个或多个html文件,需要指明具体文件名 r.LoadHTMLFiles("vie…...

#鸿蒙生态创新中心#揭幕仪式在深圳湾科技生态园举行
3 月 19 日,#鸿蒙生态创新中心#揭幕仪式在深圳湾科技生态园举行。 现场,深圳市南山区人民政府副区长李志娜发布《2024 年南山区支持鸿蒙原生应用发展首批政策措施清单》,从加强鸿蒙原生应用供给能力、推动鸿蒙原生应用产业集聚、完善鸿蒙原生…...

flask 继续学习
group_by group_by是一种在数据库查询或数据处理中常用的操作,它用于将数据按照指定的列进行分组。通过group_by操作,可以将数据集按照某个列的值进行分类,然后对每个分类进行聚合计算或其他操作。 在SQL语言中,group_by通常与聚…...

DockerFile遇到的坑
CMD 命令的坑 dockerfile 中的 CMD 命令在docker run -it 不会执行 CMD 命令。 FROM golang WORKDIR / COPY . ./All-in-one CMD ["/bin/sh","-c","touch /kkk.txt && ls -la"] RUN echo alias ll"ls -la" > ~/.bashrc(不…...
)
并网型风光储微电网日前优化调度(MATLAB实现)
考虑了光伏发电、风力发电、电池储能和负荷需求等因素,与主网相连不考虑向主网售电情况。 % 微电网日前优化调度示例代码% 定义时间步长(例如,每小时) time_steps 24;% 生成模拟数据:光伏发电量,风力发电…...
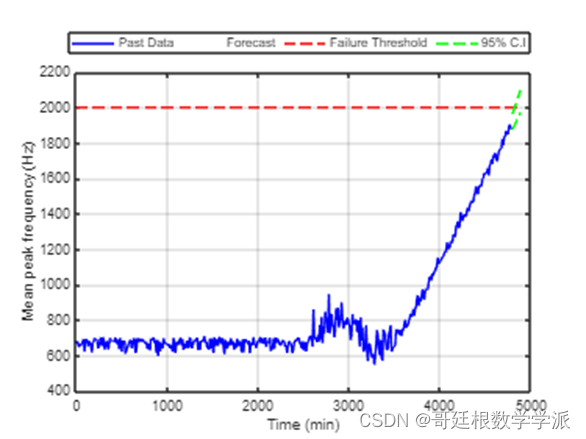
MATLAB环境下基于振动信号的轴承状态监测和故障诊断
故障预测与健康管理PHM分为故障预测和健康管理与维修两部分,PHM首先借助传感器采集关键零部件的运行状态数据,如振动信号、温度图像、电流电压信号、声音信号及油液分析等,提取设备的运行监测指标,进而实现对设备关键零部件运行状…...
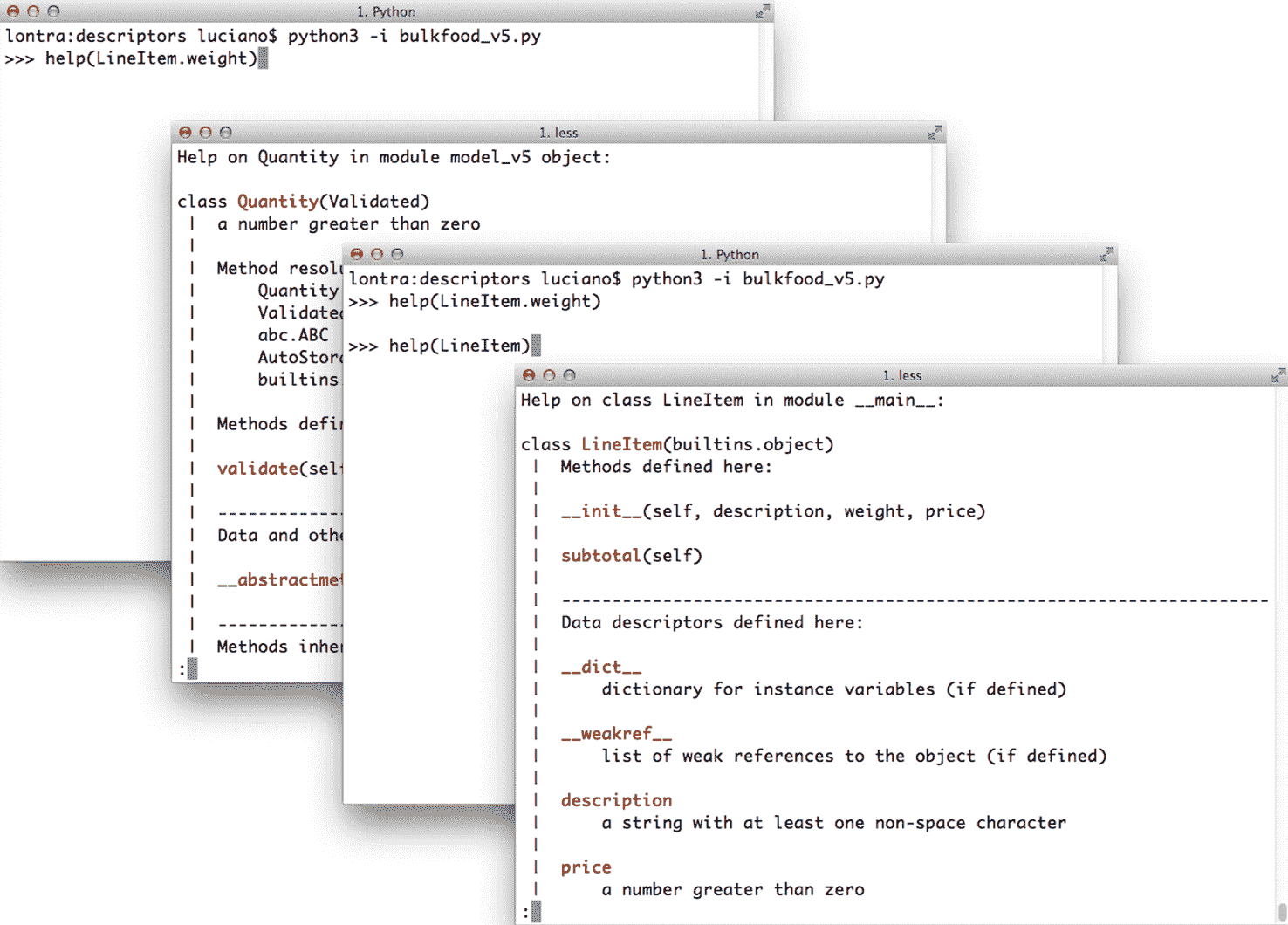
流畅的 Python 第二版(GPT 重译)(十二)
第五部分:元编程 第二十二章:动态属性和属性 属性的关键重要性在于,它们的存在使得将公共数据属性作为类的公共接口的一部分完全安全且确实可取。 Martelli、Ravenscroft 和 Holden,“为什么属性很重要” 在 Python 中࿰…...

【Python 48小时速成 2】关键字
文章目录 01. and :逻辑运算符,表示逻辑与操作。02. exec :内置函数,用于执行存储在字符串或文件中的 Python 代码。03. not :逻辑运算符,表示逻辑非操作。04. assert :断言语句,用于…...

小程序socket 全局代码
在微信小程序中,为了实现在整个应用范围内共享一个WebSocket连接,通常会将WebSocket的创建、打开、关闭以及消息收发等功能封装在一个全局模块中,然后在各个需要使用WebSocket功能的页面中引入并调用这个模块的方法。以下是一个简化的全局Web…...

数据挖掘|数据集成|基于Python的数据集成关键问题处理
数据挖掘|数据集成|基于Python的数据集成关键问题处理 1. 实体识别2. 数据冗余与相关性分析3. 去除重复记录4. 数据值冲突的检测与处理5. 基于Python的数据集成5.1 merge()方法5.2 Concat()方法 数据集成是把来自多个数据库或文件等不同数据源的数据整合成一致的数据存储。其中…...
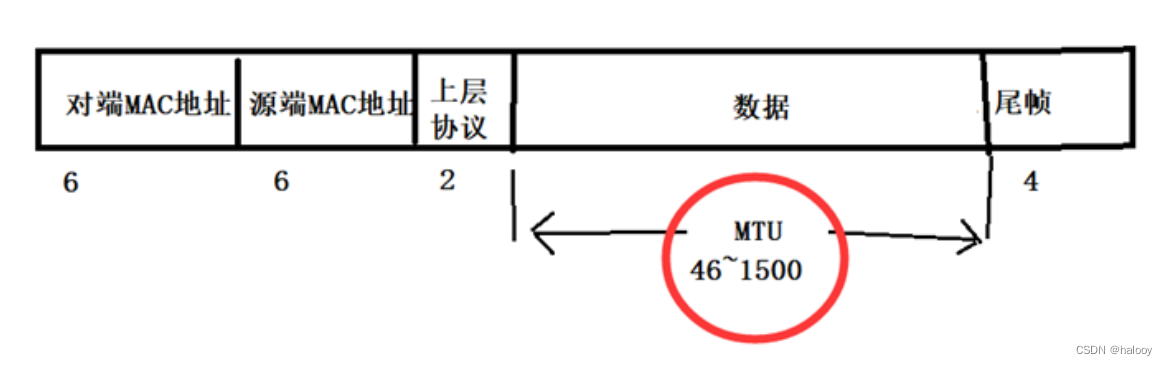
Linux-网络层IP协议、链路层以太网协议解析
目录 网络层:IP协议地址管理路由选择 链路层 网络层: 网络层:负责地址管理与路由选择 — IP协议,地址管理,路由选择 IP协议 数据格式: 4位协议版本:4-ipv4协议版本 4位首部长度:以…...

后端开发辅助
maven仓库手动添加jar命令 mvn install:install-file -DfileD:\\spire.xls-4.6.5.jar -DgroupIde-iceblue -DartifactIdspire.xls -Dversion4.6.5 -Dpackagingjaroracle调用存储过程示例 DECLAREPO_ERRCODE VARCHAR2(100);PO_ERRMSG VARCHAR2(100);BEGIN-- Call the procedure…...

插件电阻的工艺结构原理及选型参数总结
🏡《总目录》 目录 1,概述2,工作原理3,结构特点3.1,引脚设计3.2,电阻体3.3,封装4,工艺流程4.1,材料准备4.2,电阻体制作4.3,引脚焊接4.4,绝缘处理4.5,测试与筛选4.6,包装与存储...
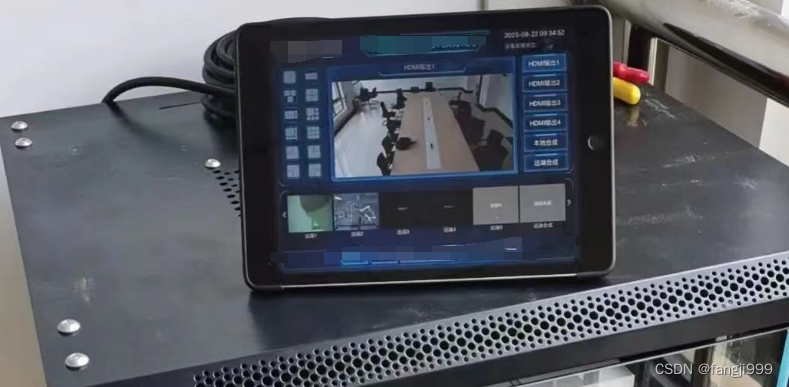
视频私有云,HDMI/AV多硬件设备终端接入,SFU/MCU视频会议交互方案。
在视频业务深入的过程中越来越多的硬件设备接入视频交互的视频会议中远程交互,有的是视频采集,有的是医疗影像等资料,都需要在终端承显,这就需要我们的设备终端能多设备,多协议接入,设备接入如下。 1&#…...

mac os 配置两个github账号
1. 清空git全局配置的username和email git config --global --unset user.name git config --global --unset user.emailgit config --list 可以查看是否清空了 2. 定义两个标识符,这两个标识符以后会被用来代替“github.com”来使用。 假设两个账号的邮箱地址分别是a@gmai…...
【SpringBoot】登录校验之会话技术、统一拦截技术
真正的登录功能应该是: 登陆后才能访问后端系统页面,不登陆则跳转登陆页面进行登陆。 当我们没有设置登录校验,可以直接通过修改地址栏直接进入管理系统内部,跳过登录页。而后端系统的增删改查功能,没有添加判断用户是…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
