Linux docker3--数据卷-nginx配置示例
一、因为docker部署服务都是以最小的代价部署,所以通常在容器内部很多依赖和命令无法执行。进入容器修改配置的操作也比较麻烦。本例介绍的数据卷作用就是将容器内的配置和宿主机文件打通,之后修改宿主机的配置文件就相当于修改了docker进程的配置文件,不用在进入容器内修改。
本例依旧通过nginx示例
二、数据卷使用
1、查看已有的数据卷
命令:docker volume ls

2、创建数据卷
命令:docker volume create nginx_html
注:nginx我们一般需要修改配置文件,html的文件页,日志目录。所以这里我们创建三个数据卷。如果是其他服务根据需求创建对应数量的数据卷即可。

3、查看数据卷的详情
命令:docker volume inspect nginx_html
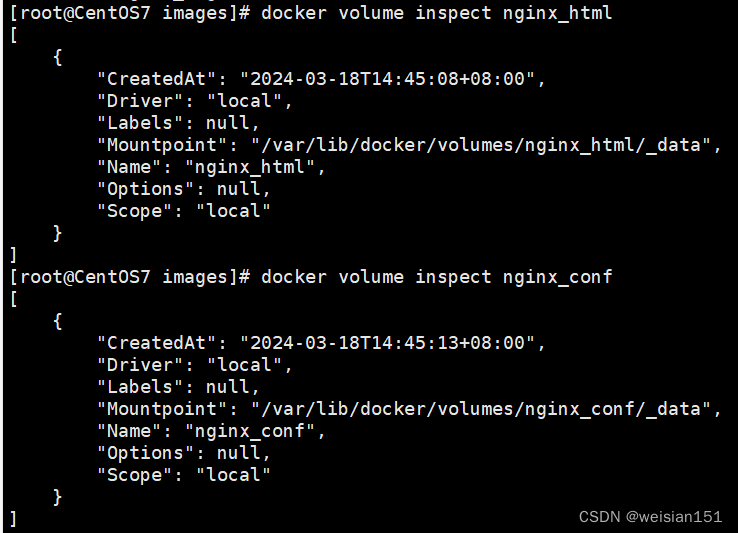
注:通过详情我们可以查看难道数据卷挂载到宿主机的实际路径(Mountpoint)。
4、删除数据卷
命令:docker volume rm nginx_test

5、关联数据卷创建容器运行nginx
docker run --name nginx_1 -p 80:80 -d -v nginx_html:/usr/share/nginx/html -v nginx_conf:/etc/nginx -v nginx_log:/var/log/nginx nginx:latest

注意:-v指定数据卷对应容器内的目录
-v nginx_html:/usr/share/nginx/html
-v nginx_conf:/etc/nginx
-v nginx_log:/var/log/nginx
6、查看和修改数据卷的挂载配置
(1)、通过上诉的详情命令,可以查看到挂载点下面已经出现了nginx的配置文件
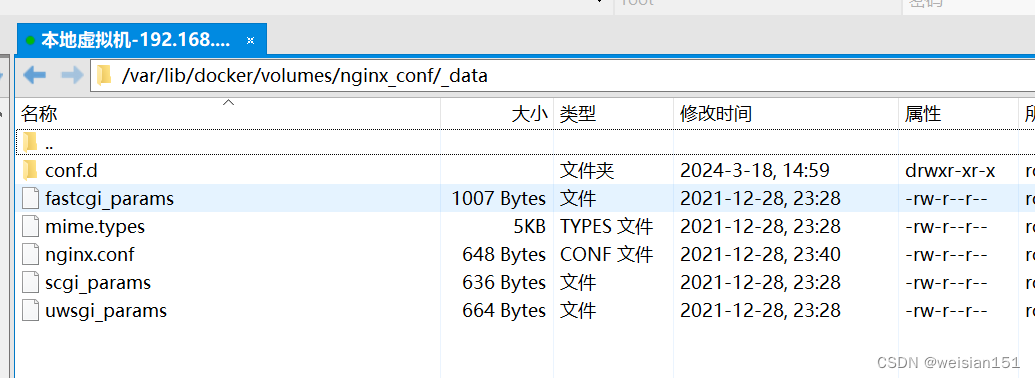
(2)、修改html的配置添加111,之后重启nginx服务
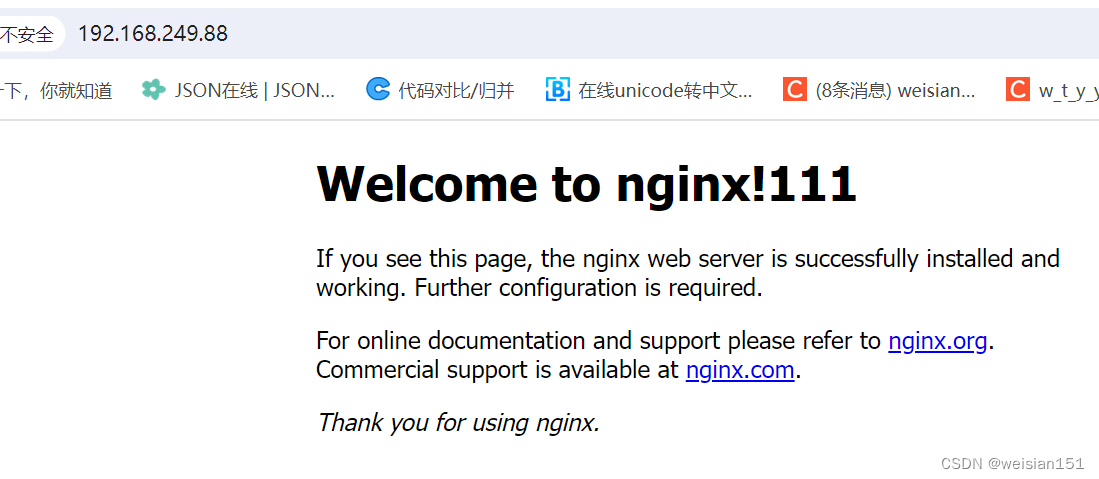
修改配置后,使用stop和start停止和重启即可。

(3)、修改配置。/baidu时,直接跳转到百度页面
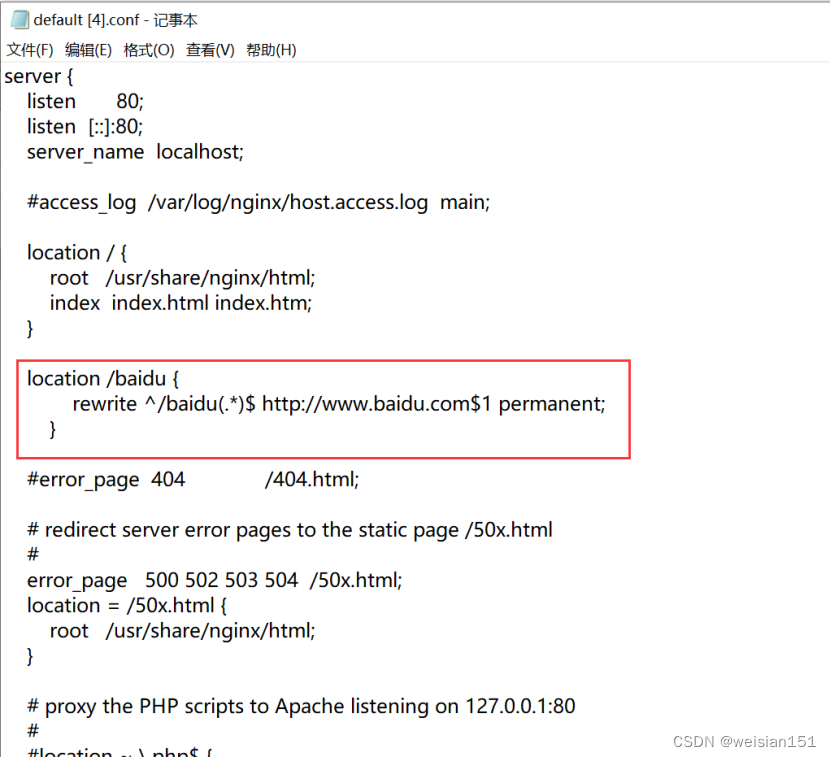
访问:192.168.248.88/baidu

以上完成了数据卷的创建,以及使用数据卷打通容器和宿主机的文件隔离,方便修改配置和重启的过程。
学海无涯苦作舟!!!
相关文章:

Linux docker3--数据卷-nginx配置示例
一、因为docker部署服务都是以最小的代价部署,所以通常在容器内部很多依赖和命令无法执行。进入容器修改配置的操作也比较麻烦。本例介绍的数据卷作用就是将容器内的配置和宿主机文件打通,之后修改宿主机的配置文件就相当于修改了docker进程的配置文件&a…...

力扣454. 四数相加 II
思路:把四个数组拆成两对,两个分别相加,记录第一对的相加结果进map里,再把第二对数组 0-nums2-nums4 去map里面找出现了几次,这题不用对重复的四元组去重,所以出现多次都有效。 class Solution {public int…...
vulnstack1 渗透分析 红日靶场(一)
环境搭建 ip段设置 kali (coleak):192.168.145.139 Windows 7 (stu1):192.168.10.181、192.168.145.140 Winserver 2008 (owa):192.168.10.180 Win2k3 (root-tvi862ubeh):192.168.10.182复制 kali可以访问win7,但不能…...
外包干了6天,技术明显进步。。。
我是一名大专生,自19年通过校招进入湖南某软件公司以来,便扎根于功能测试岗位,一晃便是近四年的光阴。今年8月,我如梦初醒,意识到长时间待在舒适的环境中,已让我变得不思进取,技术停滞不前。更令…...

比较好的知识点
2023年Java超全面试题及答案解析---https://blog.csdn.net/qq_42301302/article/details/128785274 7分钟带你细致解析4个Java算法必刷题---https://blog.csdn.net/hcxy2022/article/details/127963797 50道JAVA基础算法编程题【内含分析、程序答案】---https://blog.csdn.net/…...
抖音开放平台的订单类API接口调用测试指南(内含详细步骤)
一、什么是抖音开放平台 抖音开放平台基于抖音母体,提供抖音服务基础设施和创新行业解决方案的平台。同时满足各类各类机构、创作者及服务商对于内容获取、分享的个性化需求,我们诚邀各个行业、不同阶段的合作伙伴与我们一起,共建内容良性生…...

HiveSQL一本通 - 案例实操
文章目录 0.HiveSQL一本通使用说明6.综合案例练习之基础查询6.1 环境准备创建数据表数据准备加载数据 6.2 简单查询练习1.查询姓名中带“山”的学生名单2.查询姓“王”老师的个数3.检索课程编号为“04”且分数小于60的学生的分数信息,结果按分数降序排列4.查询数学成…...
Axure RP 8中文---快速原型设计工具,一站式解决方案
Axure RP 8是一款专业的快速原型设计工具,以其直观易用的界面和丰富的功能受到广大用户的青睐。它支持用户通过拖放操作快速创建交互式原型,包括线框图、流程图等,并具备高保真度的设计能力。Axure RP 8还提供了团队协作和共享功能࿰…...

Available platform plugins are: minimal, offscreen, webgl, windows.
我在运行pyqt5开发的代码时,报错: This application failed to start because no Qt platform plugin could be initialized, Reinstalling the application may fix this problem. Available platform plugins are: minimal, offscreen, webgl, windows…...

创意无限,风险有度:2024愚人节海外网红营销策略解析
2024年愚人节即将到来,这个充满趣味与惊喜的节日,既是人们展示幽默与创意的舞台,也是品牌进行营销活动的绝佳时机。在这个特殊的日子里,通过海外网红营销来推广品牌或产品,无疑是一种富有创意的营销策略,但…...

深入理解 Session、Cookie 和 Token:网络安全和身份验证的重要概念
深入理解 Session、Cookie 和 Token:网络安全和身份验证的重要概念 在当今数字化的世界中,网络安全和身份验证是至关重要的议题。为了实现这些目标,我们常常使用诸如 Session、Cookie 和 Token 等概念。这些概念在 Web 开发、网络通信和安全…...

镜像站汇总
软件镜像站 查看linux版本,常见有centos, ubuntu, Debian cat /etc/os-release去清华软件源帮助页面,查找对应源设置方案(需要结合具体的系统版本),常用: Debian https://mirrors.tuna.tsinghua.edu.cn/help/debian/ 需要选则系…...

设计模式之抽象工厂模式解析
抽象工厂模式 1)问题 工厂方法模式中的每个工厂只生产一类产品,会导致系统中存在大量的工厂类,增加系统的开销。 2)概述 a)产品族 和 产品等级结构 产品等级结构:产品的继承结构; 产品族&…...

【毕设级项目】基于ESP8266的家庭灯光与火情智能监测系统——文末源码及PPT
目录 系统介绍 硬件配置 硬件连接图 系统分析与总体设计 系统硬件设计 ESP8266 WIFI开发板 人体红外传感器模块 光敏电阻传感器模块 火焰传感器模块 可燃气体传感器模块 温湿度传感器模块 OLED显示屏模块 系统软件设计 温湿度检测模块 报警模块 OLED显示模块 …...
UnityShader(十九) AlphaBlend
上代码: Shader "Shader入门/透明度效果/AlphaBlendShader" {Properties{_MainTex ("Texture", 2D) "white" {}_AlphaScale("AlphaScale",Range(0,1))1.0}SubShader{Tags { "RenderType""Transparent&quo…...

3D Tiles语义分割流水线
Dylan Chua 和 Anne Lee 开发了一个处理管线,用于对 3D Tiles 中包含的 GL 传输格式 (glTF) 模型进行语义分割。 该管道读取并遍历 3D Tileset,以输出包含元数据的经过转换的划分对象集。 该项目为 3D 语义分割器提供了最小可行产品,作为各种…...
txt、pdf等文件转为一行一行的doccano数据集输入格式
文章目录 doccano 数据集导入简介代码实现代码运行结果代码公开 doccano 数据集导入 在Doccano 导入数据集时,使用TextLine的文件格式,导入的文件需要为一行一行文本的数据格式,每一行文本在导入Doccano后就是一条数据。 简介 主要工作说明…...
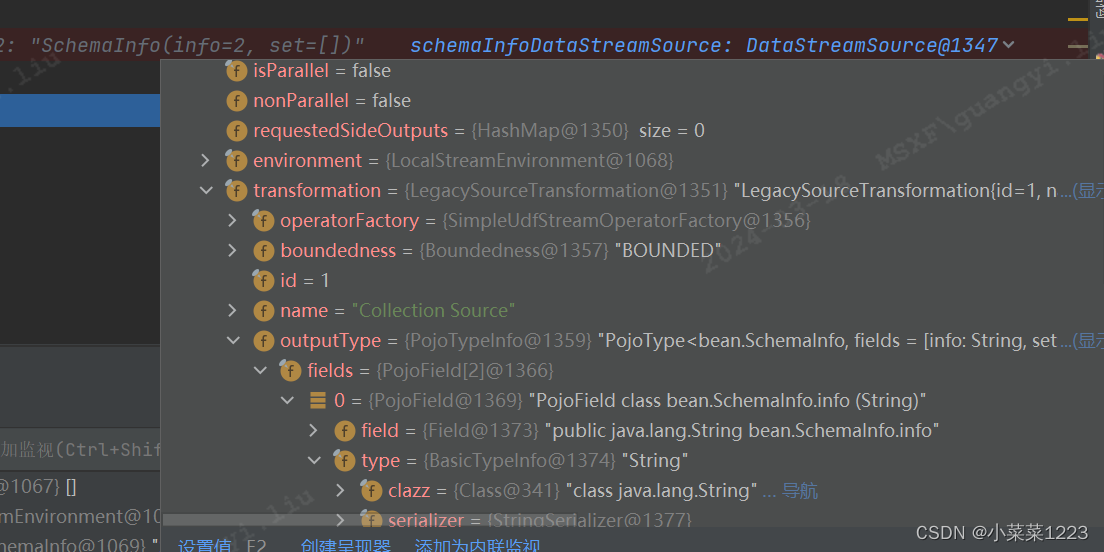
java Flink(四十二)Flink的序列化以及TypeInformation介绍(源码分析)
Flink的TypeInformation以及序列化 TypeInformation主要作用是为了在 Flink系统内有效地对数据结构类型进行管理,能够在分布式计算过程中对数据的类型进行管理和推断。同时基于对数据的类型信息管理,Flink内部对数据存储也进行了相应的性能优化。 Flin…...

社科赛斯考研:二十二载岁月铸辉煌,穿越周期的生命力之源
在考研培训行业的浩瀚海洋中,社科赛斯考研犹如一艘稳健的巨轮,历经二十二载风礼,依然破浪前行。在考研市场竞争白热化与学生对于考研机构要求越来越高的双重影响下,社科赛斯考研却以一种分蘖成长的姿态,扎根、壮大&…...

【视频图像取证篇】模糊图像增强技术之锐化类滤波场景应用小结
【视频图像取证篇】模糊图像增强技术之锐化类滤波场景应用小结 模糊图像增强技术之锐化类滤波场景应用小结—【蘇小沐】 (一)锐化类滤波器 模糊消除类滤波器(Remove blur / Unsharpness)。 通用去模糊滤波器:针对大…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
