【LeetCode: 433. 最小基因变化 + BFS】

| 🚀 算法题 🚀 |
🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀
🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨
🌲 作者简介:硕风和炜,CSDN-Java领域优质创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
🌲 人生如棋,我愿为卒,行动虽慢,可谁曾见我后退一步?🎯🎯
| 🚀 算法题 🚀 |


🍔 目录
- 🚩 题目链接
- ⛲ 题目描述
- 🌟 求解思路&实现代码&运行结果
- ⚡ BFS
- 🥦 求解思路
- 🥦 实现代码
- 🥦 运行结果
- 💬 共勉
🚩 题目链接
- 433. 最小基因变化
⛲ 题目描述
基因序列可以表示为一条由 8 个字符组成的字符串,其中每个字符都是 ‘A’、‘C’、‘G’ 和 ‘T’ 之一。
假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。
例如,“AACCGGTT” --> “AACCGGTA” 就是一次基因变化。
另有一个基因库 bank 记录了所有有效的基因变化,只有基因库中的基因才是有效的基因序列。(变化后的基因必须位于基因库 bank 中)
给你两个基因序列 start 和 end ,以及一个基因库 bank ,请你找出并返回能够使 start 变化为 end 所需的最少变化次数。如果无法完成此基因变化,返回 -1 。
注意:起始基因序列 start 默认是有效的,但是它并不一定会出现在基因库中。
示例 1:
输入:start = “AACCGGTT”, end = “AACCGGTA”, bank = [“AACCGGTA”]
输出:1
示例 2:
输入:start = “AACCGGTT”, end = “AAACGGTA”, bank = [“AACCGGTA”,“AACCGCTA”,“AAACGGTA”]
输出:2
示例 3:
输入:start = “AAAAACCC”, end = “AACCCCCC”, bank = [“AAAACCCC”,“AAACCCCC”,“AACCCCCC”]
输出:3
提示:
start.length == 8
end.length == 8
0 <= bank.length <= 10
bank[i].length == 8
start、end 和 bank[i] 仅由字符 [‘A’, ‘C’, ‘G’, ‘T’] 组成
🌟 求解思路&实现代码&运行结果
⚡ BFS
🥦 求解思路
- 题目要求我们将一个基因序列 A 变化至另一个基因序列 B,在变化的过程中需要满足以下条件:
- 序列 A 与 序列 B 之间只有一个字符不同;
- 变化字符只能从 ‘A’, ‘C’, ‘G’, ‘T‘中进行选择;
- 变换后的序列 B 一定要在字符串数组 bank中。
- 然后,我们通过bfs来尝试所有的可能,具体来说就是,先从A开始,然后判断A中的每一个字符,尝试是否可以替换为 ‘A’, ‘C’, ‘G’, ‘T‘,也就是替换一次后,bank中是否存在,如果存在,加入到队列中,如果不存在,继续向后判断。
- 有了基本的思路,接下来我们就来通过代码来实现一下。
🥦 实现代码
class Solution {public int minMutation(String start, String end, String[] bank) {Set<String> cnt = new HashSet<String>();Set<String> visited = new HashSet<String>();char[] keys = { 'A', 'C', 'G', 'T' };for (String w : bank) {cnt.add(w);}if (start.equals(end)) {return 0;}if (!cnt.contains(end)) {return -1;}Queue<String> queue = new ArrayDeque<String>();queue.offer(start);visited.add(start);int step = 1;while (!queue.isEmpty()) {int sz = queue.size();for (int i = 0; i < sz; i++) {String curr = queue.poll();for (int j = 0; j < curr.length(); j++) {for (int k = 0; k < 4; k++) {if (keys[k] != curr.charAt(j)) {StringBuffer sb = new StringBuffer(curr);sb.setCharAt(j, keys[k]);String next = sb.toString();if (!visited.contains(next) && cnt.contains(next)) {if (next.equals(end)) {return step;}queue.offer(next);visited.add(next);}}}}}step++;}return -1;}
}
🥦 运行结果
💬 共勉
| 最后,我想和大家分享一句一直激励我的座右铭,希望可以与大家共勉! |


相关文章:

【LeetCode: 433. 最小基因变化 + BFS】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
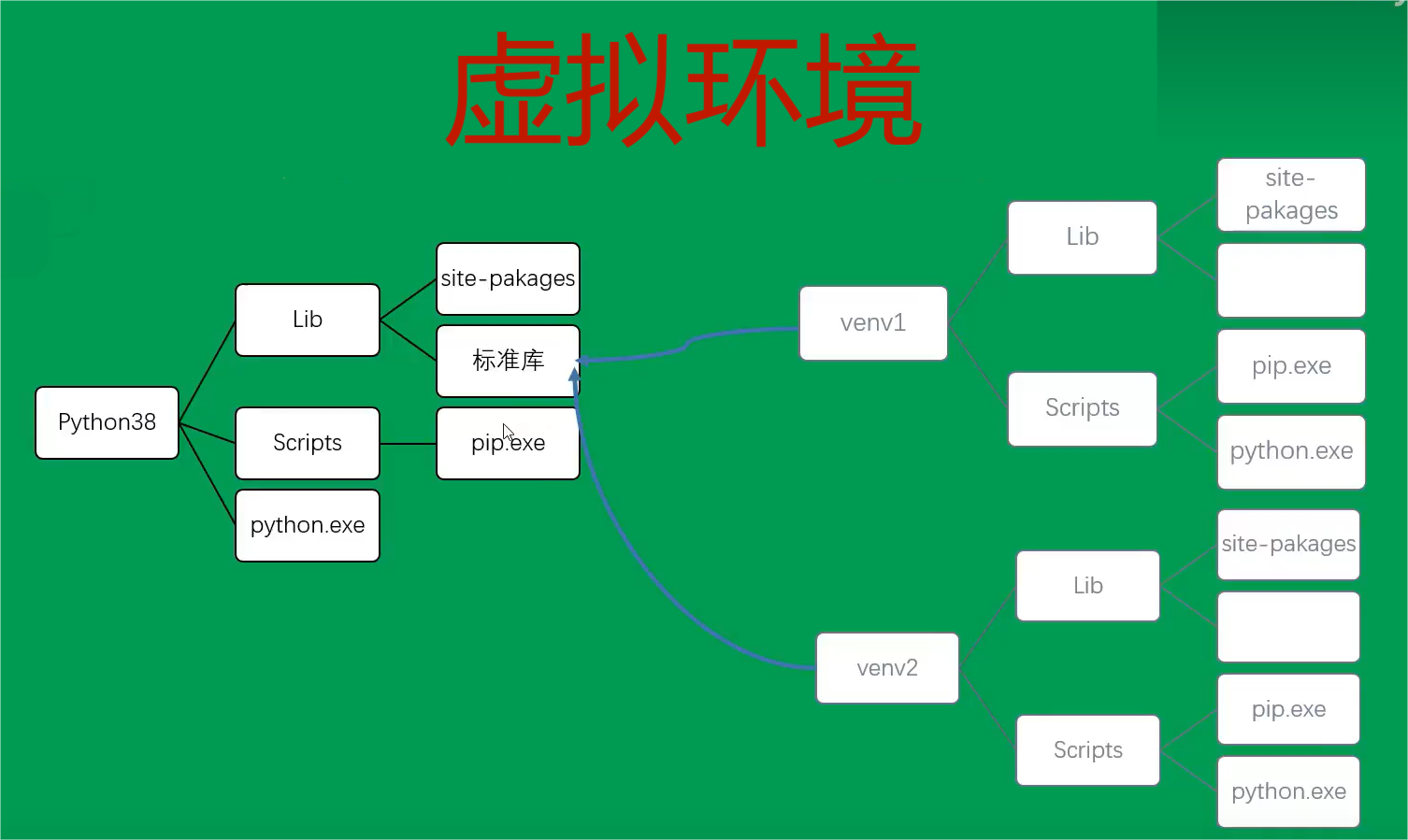
Python 安装目录及虚拟环境详解
Python 安装目录 原文链接:https://blog.csdn.net/xhyue_0209/article/details/106661191 Python 虚拟环境 python 虚拟环境图解 python 虚拟环境配置与详情 原文链接:https://www.cnblogs.com/hhaostudy/p/17321646.html...

linux sh脚本编写
linux中bash Shell 是 Linux 的核心部分,它允许你使用各种诸如 cd、ls、cat 等的命令与 Linux 内核进行交互。Bash脚本和Shell脚本实际上是指同一种类型的脚本,只不过Bash是其中最常用的一种Shell。除了Bash之外,常见的Shell解释器还有C She…...
|28. 实现 strStr()、459.重复的子字符串、KMP算法)
代码随想录笔记|C++数据结构与算法学习笔记-字符串(二)|28. 实现 strStr()、459.重复的子字符串、KMP算法
文章目录 卡码网.右旋字符串28. 实现 strStr()KMP算法(理论)KMP算法(代码)C代码 459.重复的子字符串暴力解法移动匹配KMP解法 卡码网.右旋字符串 卡码网题目链接 略 28. 实现 strStr() 力扣题目链接 文字链接:28. 实现 strStr() 视频链接:帮你把KMP算法…...
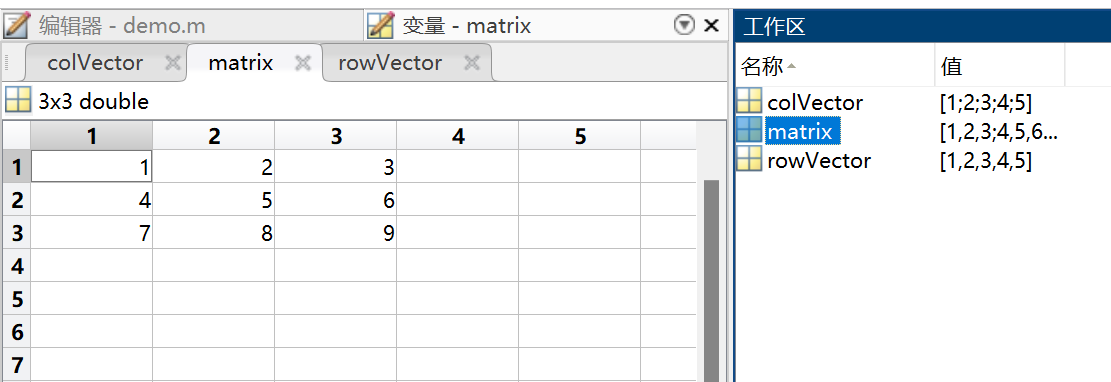
【复杂网络建模】——建模工具Matlab入门
目录 一、认识MATLAB 二、认识工具箱 三、基本操作和函数 3.1 算术操作符 3.2 数学函数 3.3 矩阵操作 3.4 索引和切片 3.5 逻辑操作 3.6 控制流程 3.7 数据输入输出 四、变量和数据类型 4.1 数值类型 4.2 整型 4.3 复数 4.4 字符串 4.5 逻辑类型 4.6 结构体&a…...

JVM面试篇
面试篇就是复习前面学的 什么是JVM 1.定义:JVM指的是Java虚拟机,本质是一个运行在计算机上的程序 2.作用:为了支持Java中Write Once ,Run Anywhere 编写一次 到处运行的跨平台特性 功能: 1.解释和运行 2.内存管理…...
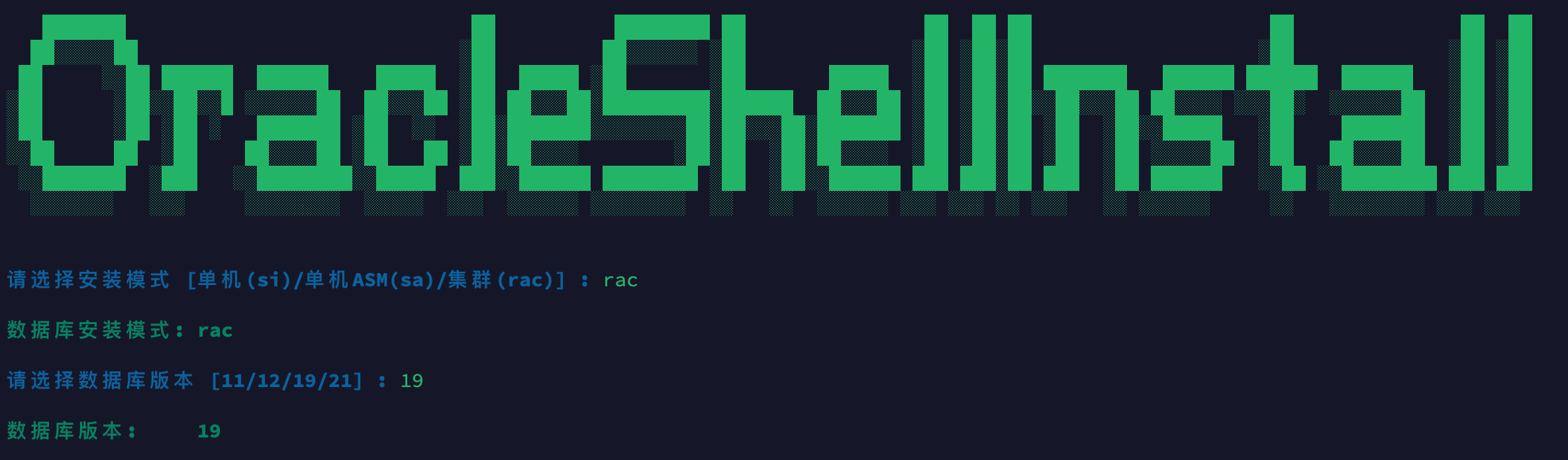
openEuler 22.03(华为欧拉)一键安装 Oracle 19C RAC(19.22) 数据库
前言 Oracle 一键安装脚本,演示 openEuler 22.03 一键安装 Oracle 19C RAC 过程(全程无需人工干预):(脚本包括 ORALCE PSU/OJVM 等补丁自动安装) ⭐️ 脚本下载地址:Shell脚本安装Oracle数据库…...

蓝桥杯刷题记录之数字王国之军训排队
记录 卡了半天,check函数中的temp % ele 0写成了ele % temp 0就挺无语的 思路 这个晚上在补 代码 import java.util.*; public class Main{static List<List<Integer>> que new ArrayList<>();static int MIN Integer.MAX_VALUE;static i…...
Go语言学习Day1:什么是Go?
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 目录 1、走近Go①Go语言的Logo②Go语言的创始人③Go语…...

C语言内存函数之 memcmp函数
memcmp函数的记忆:mem表示内存,单位是字节,表示以单位字节来进行操作;头文件是string.h,cmp是compare的缩写,表示比较。总的意思就是在规定的内存下以字节为单位一个字节一个字节的进行比较。 memcmp函数的…...

3. C++ 常见的段错误及对策
常见的 C/C 段错误及对策 一、指针没有指向一块合法的内存 定义了指针变量,但是没有为指针分配内存,即指针没有指向一块合法的内存。这里举几个比较隐蔽的例子。 结构体成员指针未初始化;没有为结构体指针分配足够的内存;函数的…...

推荐的Kubernetes 学习资料
官方文档: Kubernetes 官方文档:https://kubernetes.io/docs/Kubernetes 教程:https://kubernetes.io/docs/tutorials/ 书籍: Kubernetes in Action,Marko Luksa 著Kubernetes Up and Running,Kelsey Hi…...
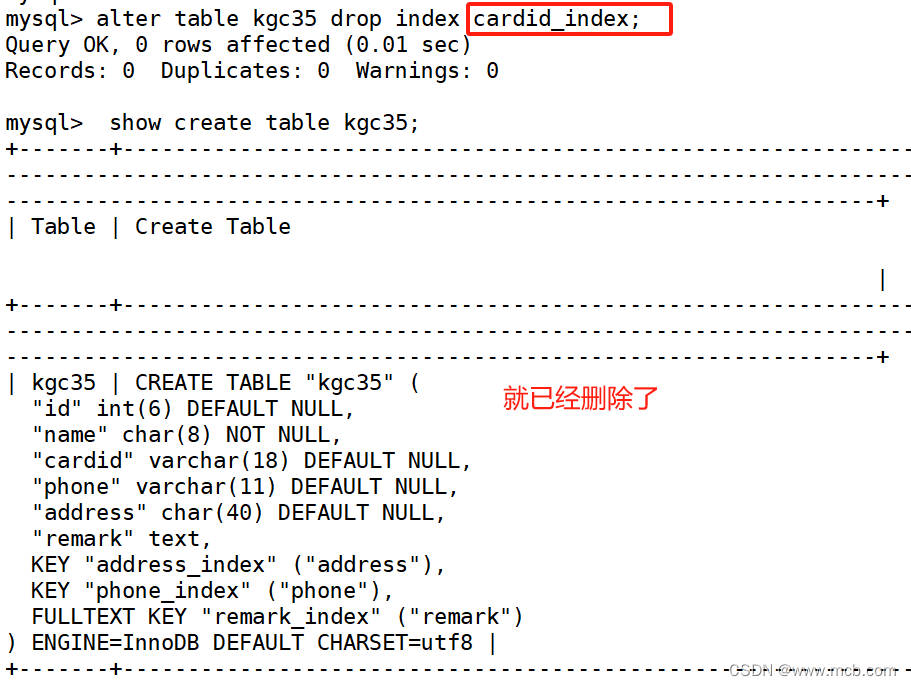
MySQL之索引与事务
一 索引的概念 一种帮助系统查找信息的数据 数据库索引 是一个排序的列表,存储着索引值和这个值所对应的物理地址无须对整个表进行扫描,通过物理地 址就可以找到所需数据是表中一列或者若干列值排序的方法 需要额外的磁盘空间 索引的作用 1 数据库…...

Linux的基本使用
1.Linux的背景 1.1什么Linux Linux是⼀个操作系统.和Windows是"并列"的关系. 1.2Linux系统的优势 1. 开源(意味着免费,便宜) 2. 稳定(Linux可以运⾏很多年,都不会发⽣重⼤问题) 3. 安全(Linux只有管理员或者特定⽤⼾才能访问Linux内核) 4. ⾃由(不会被强加商业产品和…...

亚信安慧AntDB全景观察:数据库领域的创新者
随着大数据时代的到来,对数据库的需求愈发强烈。在这一背景下,国产数据库逐渐崭露头角,亚信安慧AntDB作为重要的代表产品之一正积极参与到激烈的市场竞争中。亚信安慧AntDB不仅追求技术的革新和突破,同时也致力于满足用户日益增长…...
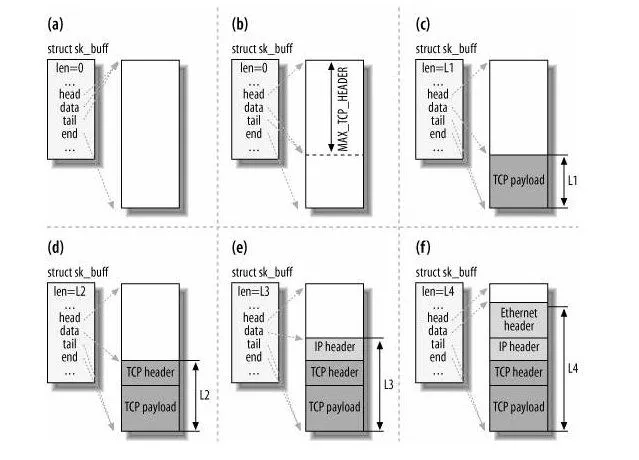
Linux 系统是如何收发⽹络包的
Linux 系统是如何收发⽹络包的? ⽹络模型 为了使得多种设备能通过⽹络相互通信,和为了解决各种不同设备在⽹络互联中的兼容性问题,国际标准化组织制定了开放式系统互联通信参考模型(Open System Interconnection Reference Mode…...

飞跃前端瓶颈:技术进阶指南精华篇
引言: 在互联网的快车道上,前端技术日新月异。对于前端工程师而言,技术水平达到一定高度后,往往会遭遇成长的天花板。本文将探讨如何识别并突破这些技术瓶颈,分享实用的进阶策略和实践案例。 一、技术等级概览…...
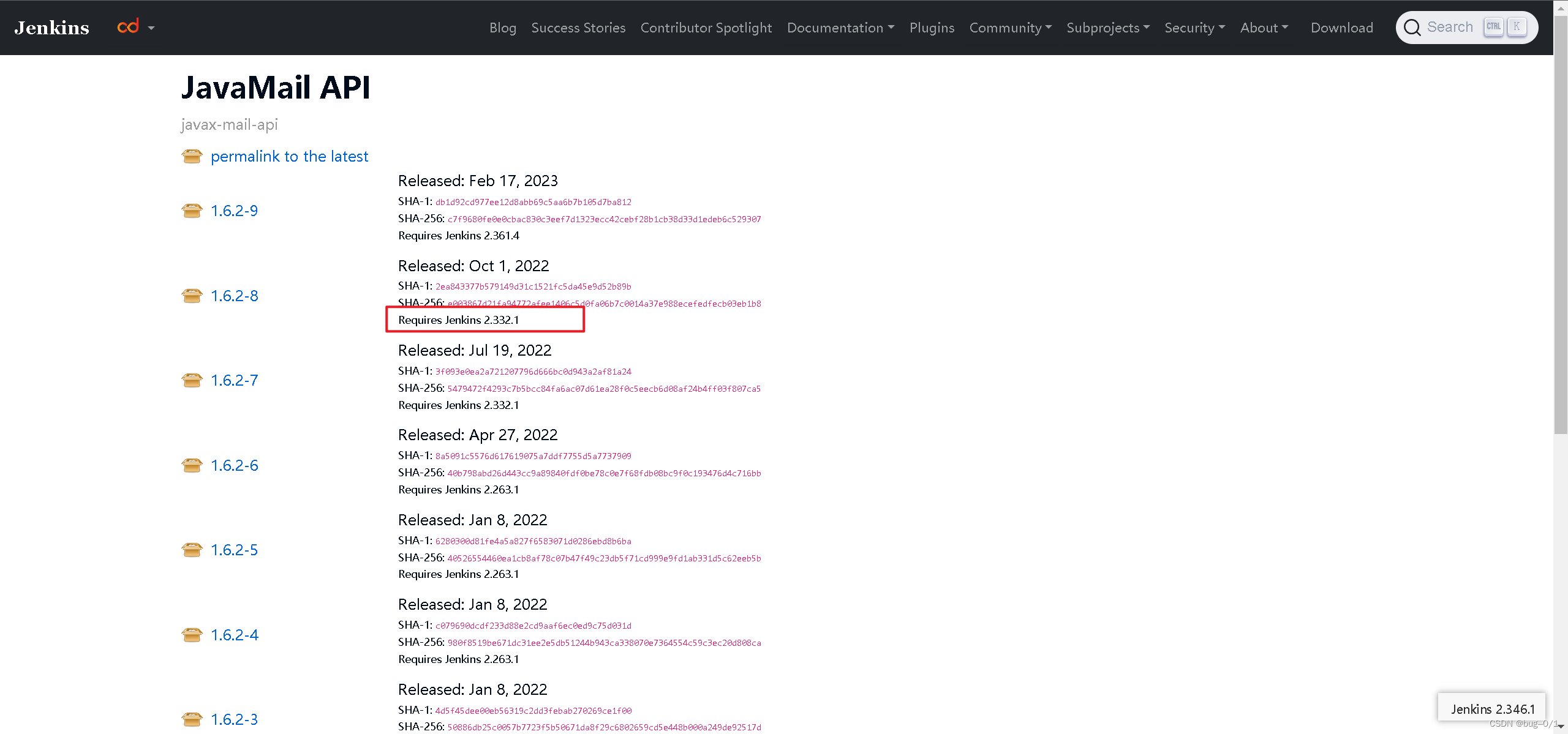
Jenkins安装 Linux 更换镜像 安装插件
Jenkins安装 Linux 更换镜像 安装插件 前言 下面叙述了三种jenkins安装的方式,jenkins安装之前必须有java环境因为他是java写的… yum安装只能安装最新版本的jenkins,但是jenkins是java写的所以他强依赖java版本,当你的服务器的java版本与jenkins版本冲突时还需要给jenkins重…...
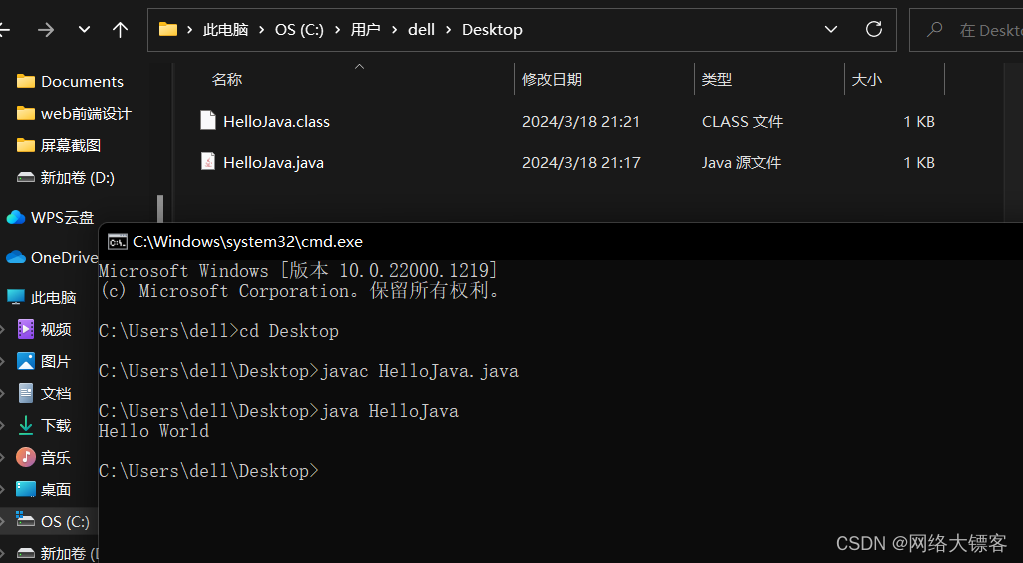
(一)基于IDEA的JAVA基础1
Java是一门面向对象的编程语言,不仅吸收了C语言的各种优点,还摒弃了C里难以理解的多继承、指针等概念,因此Java语言具有功能强大和简单易用两个特征。Java语言作为静态面向对象编程语言的代表,极好地实现了面向对象理论࿰…...

FPGA开源项目分享——基于FPGA加速的热扩散模拟器
导语 今天继续分享康奈尔大学FPGA课程ECE 5760的典型案例——基于FPGA加速的热扩散模拟器。 (更多其他案例请参考网站: Final Projects ECE 5760) 1. 项目概述 项目网址 https://people.ece.cornell.edu/land/courses/ece5760/FinalProje…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
