力扣由浅至深 每日一题.10 最后一个单词的长度
日子都是崭新的,我们下一章见 ——24.3.21
最后一个单词的长度
给你一个字符串
s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。单词 是指仅由字母组成、不包含任何空格字符的最大
子字符串
示例 1:
输入:s = "Hello World" 输出:5 解释:最后一个单词是“World”,长度为5。示例 2:
输入:s = " fly me to the moon " 输出:4 解释:最后一个单词是“moon”,长度为4。示例 3:
输入:s = "luffy is still joyboy" 输出:6 解释:最后一个单词是长度为6的“joyboy”。
方法一:反向遍历
题目要求得到字符串中最后一个单词的长度,可以反向遍历字符串,寻找最后一个单词并计算其长度。
由于字符串中至少存在一个单词,因此字符串中一定有字母。首先找到字符串中的最后一个字母,该字母即为最后一个单词的最后一个字母。
从最后一个字母开始继续反向遍历字符串,直到遇到空格或者到达字符串的起始位置。遍历到的每个字母都是最后一个单词中的字母,因此遍历到的字母数量即为最后一个单词的长度。
class Solution {public int lengthOfLastWord(String s) {//寻找最后一个字符串数组中最后一个字符串(单词)的起始位置int index = s.length() - 1;//找到最后一个单词的起始位置while (s.charAt(index) == ' ') {index--;}//定义最后一个单词的长度int wordLength = 0;//判断字符串数组位置是否合法,且中途不会遇到空格while (index >= 0 && s.charAt(index) != ' ') {//记录最后一个单词的长度的变量++wordLength++;//最后一个单词遍历的次数--index--;}return wordLength;}
}方法二:split方法
split方法简介:http://t.csdnimg.cn/4NMo6
split方法:在日常代码编写中,通过split方法来确定分隔符然后分割字符串,将字符串分割为一个个字符
此题用split方法将字符串分割为一个个单词并存入一个字符串数组,再取字符串数组的最后一个元素的下标,.length方法求最后一个字符串的长度,对题目进行求解
class Solution {public int lengthOfLastWord(String s) {//split方法,将字符串用split()中的符号分割开,组成字符串数组String[] cnt=s.split(" ");//.length方法找到最后字符串数组中最后一个字符串并计算长度return cnt[cnt.length-1].length();}
}方法三:拆分后再遍历
用split()方法分割字符串,用数组下标记录最后一个字符串,定义一个存储最后一个字符串长度的变量,当遍历到最后一个字符串的最后一个字符时,证明已经记录完毕,返回变量所记录的值
class Solution {public int lengthOfLastWord(String s) {String[] s1 = s.split(" ");s=s1[s1.length-1];int count=0;for(int i=0;i<s.length();i++){if(s.charAt(i)!=' '){count++;}}return count;}
}
相关文章:

力扣由浅至深 每日一题.10 最后一个单词的长度
日子都是崭新的,我们下一章见 ——24.3.21 最后一个单词的长度 给你一个字符串 s,由若干单词组成,单词前后…...
21 OpenCV 直方图均衡化
文章目录 直方图概念均衡的目的equalizeHist 均衡化算子示例 直方图概念 图像直方图,是指对整个图像像在灰度范围内的像素值(0~255)统计出现频率次数,据此生成的直方图,称为图像直方图-直方图。直方图反映了图像灰度的分布情况。 均衡的目的…...
对七层代理、四层代理、正向代理、反向代理的认识
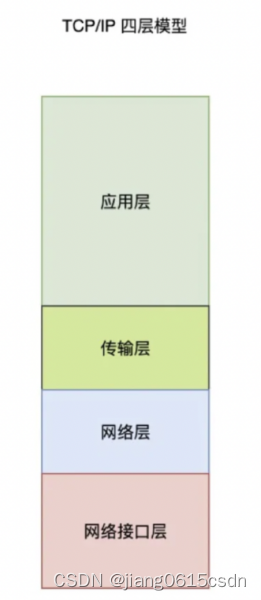
一、理解nginx服务代理 Nginx代理有正向和反向代理两种类型,可以基于osi七层模型中的第四层(传输层)和第七层(应用层)进行代理 注: nginx 一般支持的是7层代理,支持四层代理一般使用 lvs 或者ha…...
网络: 五种IO模型
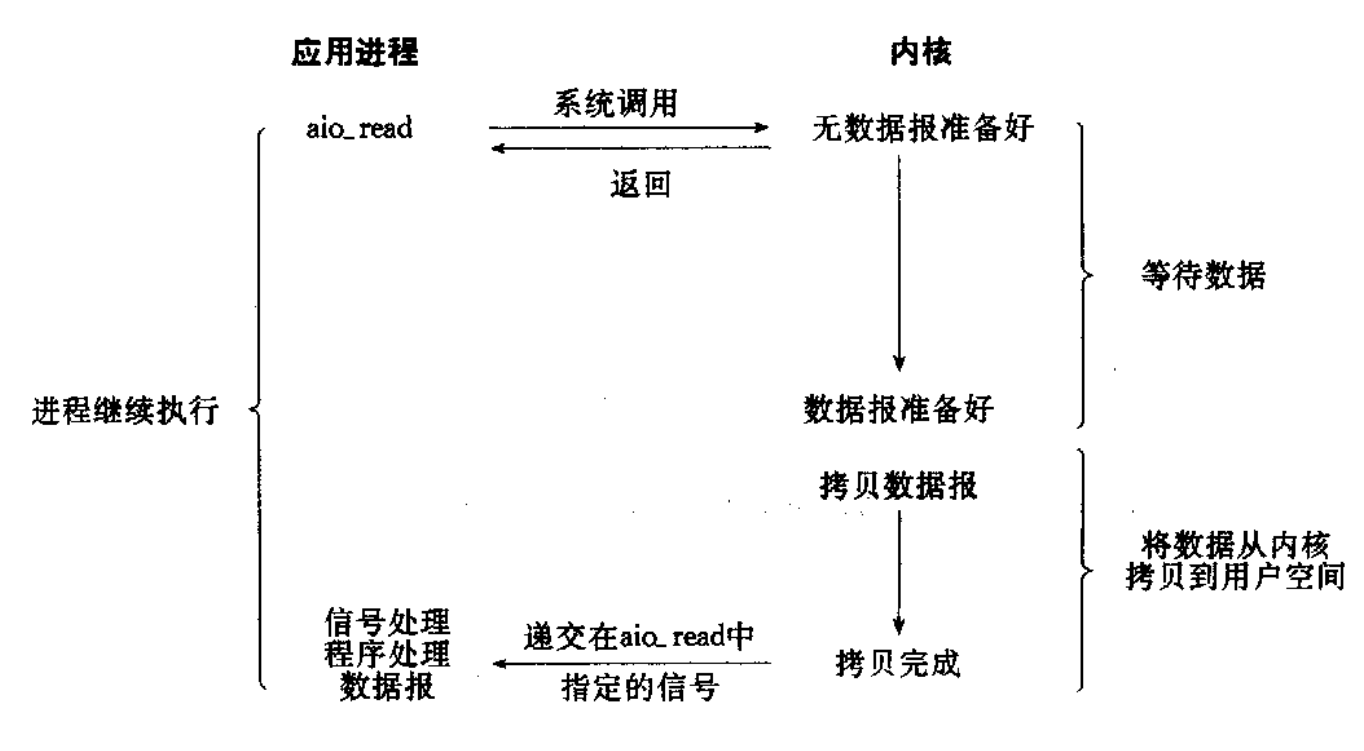
阻塞IO: 在内核将数据准备好之前, 系统调用会一直等待. 所有的套接字, 默认都是阻塞方式 非阻塞IO:若内核还未将数据准备好, 系统调用仍然会直接返回, 并且返回EWOULDBLOCK错误码. 信号驱动: 内核将数据准备好的时候, 使用SIGIO信号通知应用程序进行IO操作 多路转接: 能够同时等…...

AI大模型学习在当前技术环境下的重要性与发展前景
目录 前言1 学科基础与技能要求1.1 数学基础的深厚性1.2 编程能力的必要性1.3 对特定领域业务场景的了解 2 模型结构与算法的优化2.1 模型结构的不断演进2.2 算法优化的重要性2.3 准确性与效率的提升 3 AI大模型学习的应用场景3.1 自然语言处理3.2 计算机视觉3.3 推荐系统 结语…...

【呼市经开区建设服务项目水、电能耗监测 数采案例】
实施方案 针对能耗采集中的水、电能源数据采集,因客观因素条件,数据采集方面存在较大难度。大多数国网电表485接口由于封签限制,不能实施采集,不让拆机接线,采集实施存在困难。水量能耗采集,存在类似问题&a…...

深度学习算法工程师面试常见问题及解答
基础知识和理论: 解释什么是深度学习以及它与机器学习的关系。描述神经网络的基本结构和工作原理。什么是反向传播算法,它是如何工作的?激活函数的作用是什么?常见的激活函数有哪些?什么是损失函数?常见的损…...

OKR与敏捷开发、精益创业等方法如何协同工作?
在快速变化的市场环境中,企业需要更加灵活和高效地应对各种挑战。目标与关键成果法(OKR)、敏捷开发以及精益创业等方法,作为现代企业管理的重要工具,各自在推动企业发展、提高团队效率、优化产品迭代等方面发挥着不可或…...

【ESP32 Arduino】定时器的使用
文章目录 前言一、ESPTIMER定时器的介绍1.1 定时器是什么 二、分频系数2.1 为什么需要分频系数2.2 分频系数怎么计算 三、定时器的使用3.1 初始化定时器对象3.2 设置中断时间3.3 设置回调函数3.4 使能定时器 四、示例代码总结 前言 在嵌入式系统中,定时器是一项重要…...
网络基础(一)初识
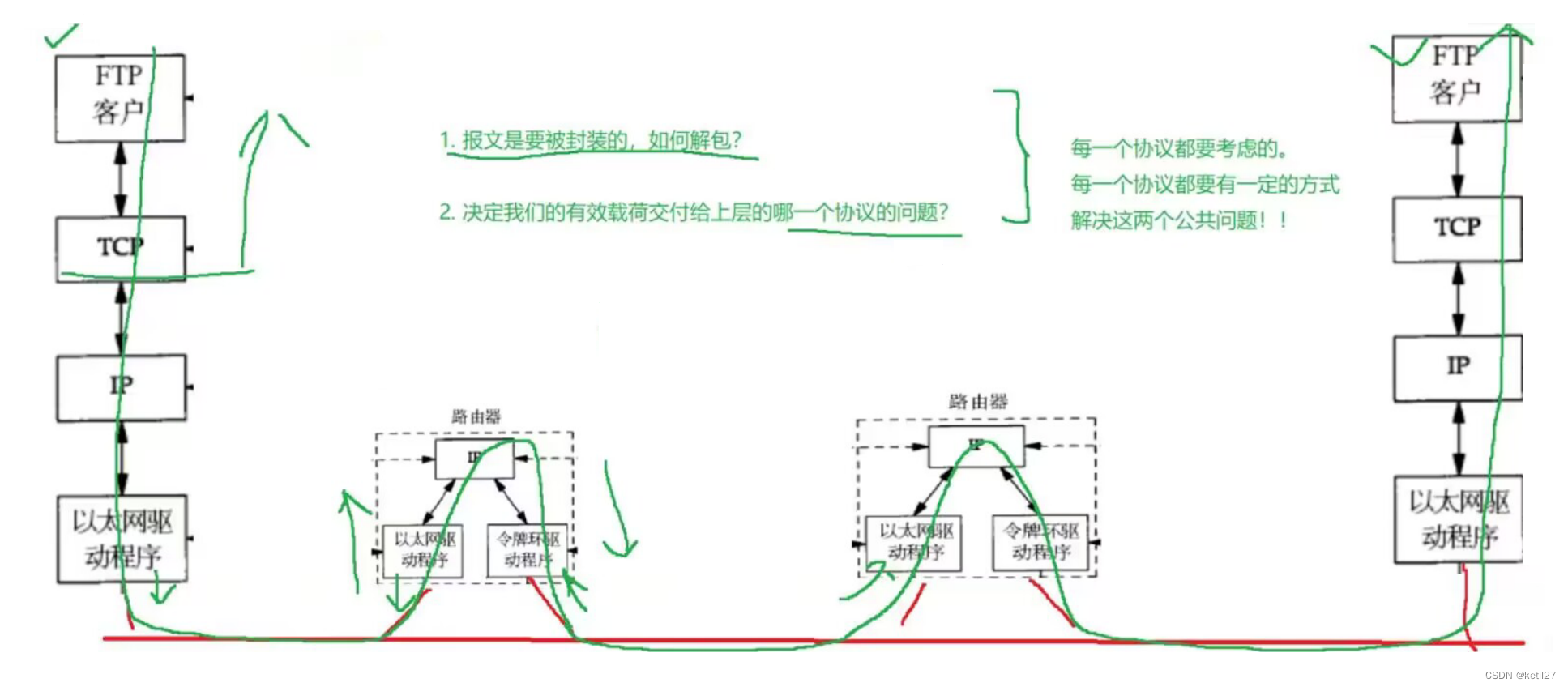
1、计算机网络背景 1.1、网络发展 1. 独立模式: 计算机之间相互独立; 2. 网络互联: 多台计算机连接在一起,完成数据共享; 3. 局域网LAN: 计算机数量更多了, 通过交换机和路由器连接在一起; 4. 广域网WAN: 将远隔千里的计算机都连在一起;…...

作业:基于udp的tftp文件传输实例
#include <head.h> #include <sys/types.h> #include <sys/socket.h> #include <arpa/inet.h> #include <errno.h>#define PORT 69 //服务器绑定的端口号 #define IP "192.168.1.107" //服务器的IP地址int do_download(i…...

【数据结构和算法】-贪心算法
贪心算法(又称贪婪算法)是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是全局最好或最优的算法。贪心算法在有最优子结构的问题中尤为有效,它通过将问题分解为一系列…...

路由器里如何设置端口映射?
在互联网时代,我们经常需要将内部网络的服务暴露到公网以便其他人访问。直接将内部网络暴露在公网上存在一定的安全风险。为了解决这个问题,我们可以利用路由器里设置端口映射来实现将特定端口的访问请求转发到内部网络的特定设备上。 端口映射的原理 端…...

M3C芯片——支持工业级HMI应用,集成2D加速、4路串口及2路CAN
M3C芯片是一款基于 RISC-V 的高性能、国产自主、工业级高清显示与智能控制 MCU,配备强大的 2D 图形加速处理器、PNG/JPEG 解码引擎、丰富的接口,支持工业宽温,具有高可靠性、高开放性,可广泛应用于工业自动化控制、HMI人机交互、 …...
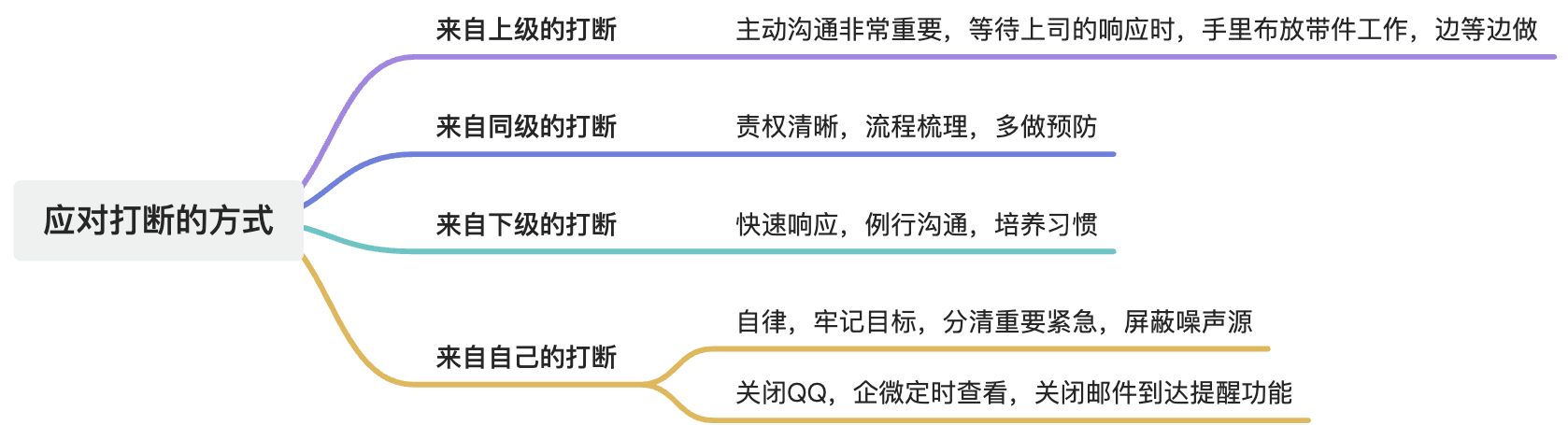
如何做时间管理?
前言 本篇是最近学习工作提效系列课程的第一篇,如何做时间管理?关于时间管理的内容老生常谈了,我自己之前也分享过针对时间管理的一些思考,比如 近期对「时间管理」的一些思考, 还有高效能人士的七个习惯的分享【读书…...

三级数据库技术考点(详解!!)
1、 答疑:【解析】分布式数据库系统按不同层次提供的分布透明性有:分片透明性;②位置透明性;③局部映像透明性,位置透明性是指数据分片的分配位置对用户是透明的,用户编写程序时只需 要考虑数据分片情况,不需要了解各分片在各个场地的分配情…...
【技术栈】Redis 企业级解决方案
SueWakeup 个人主页:SueWakeup 系列专栏:学习技术栈 个性签名&…...
(一)Linux+Windows下安装ffmpeg
一丶前言 FFmpeg是一个开源的音视频处理工具集,由多个命令行工具组成。它可以在跨平台的环境中处理、转换、编辑和流媒体处理音视频文件。 FFmpeg支持多种常见的音视频格式和编解码器,可以对音视频文件进行编码、解码、转码、剪辑、合并等操作。它具有广…...
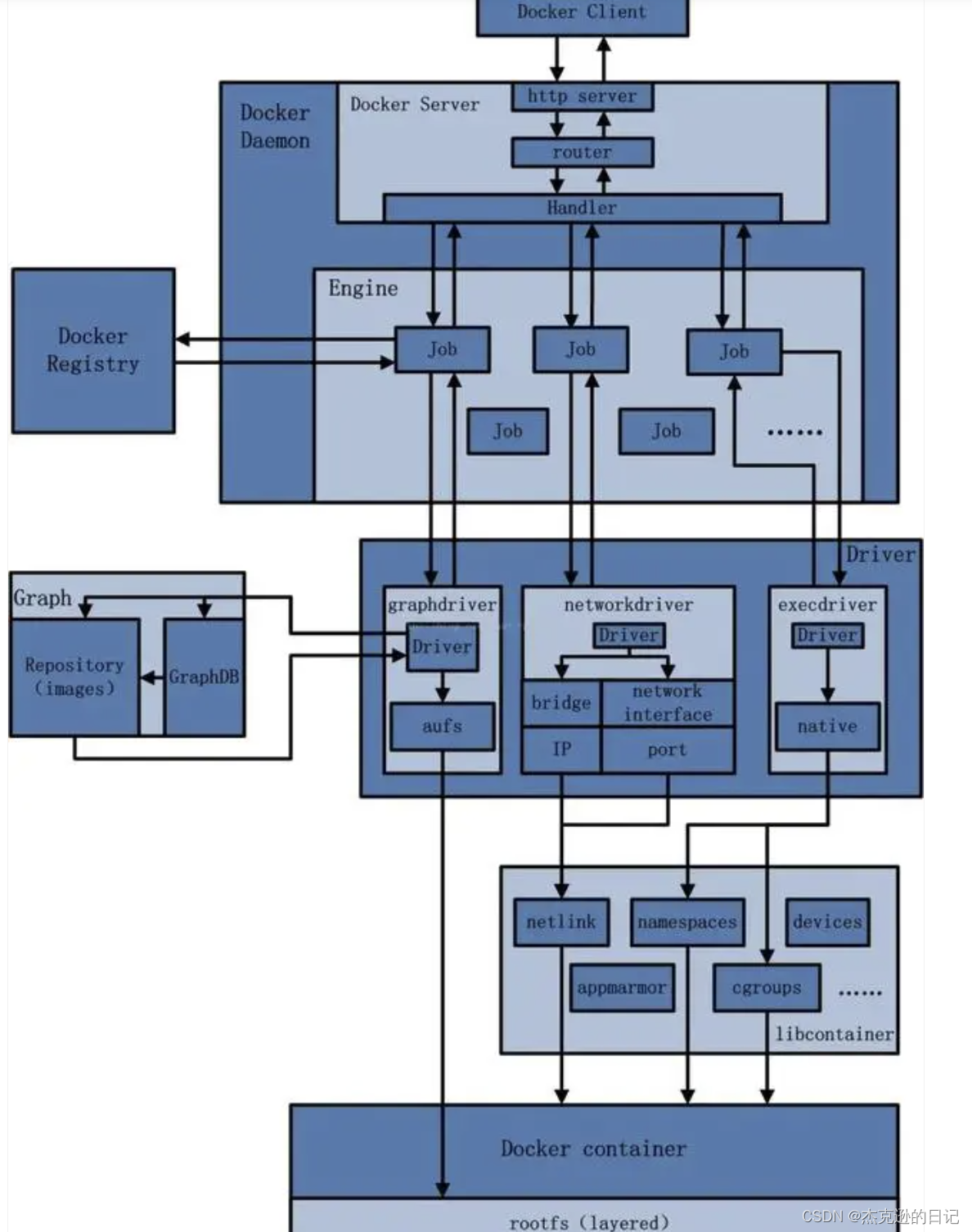
docker的部署与安装以及部署一个docker(容器)应用及docker容器常出现的问题
docker 架构图 一、docker的部署与安装 1、在 CentOS 上安装 Docker 移除旧版本(如果有的话):sudo yum remove docker docker-client docker-client-latest docker-common docker-latest docker-latest-logrotate docker-logrotate docker-…...

harmonyOS简介及背景
harmonyOS的场景模式18n: 1(入口手机)8(电脑、VR、手环、iPad、智慧屏、)–wifi—n(车载、智能家居等所有)harmonyOS不需要考虑软硬件的差异,是一个兼容N种的超级终端harmonyOS干了两件事: (1&a…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
