【每日一题】好子数组的最大分数
Tag
【单调栈】【暴力枚举】【数组】【2024-03-19】
题目来源
1793. 好子数组的最大分数

解题思路
本题和 84. 柱状图中最大的矩形 一样,计算的都是最大矩形的面积。只不过多了一个约束:矩形必须包含下标 k。
以下的方法一和方法二是 84. 柱状图中最大的矩形 的解法。我将在方法二中增加一个判断条件即可解答本题。
方法一:暴力枚举
思路
为了找出柱状图中最大的矩形,我们可以枚举矩形的宽和高。
如果我们枚举「宽」,我们需要用到两层循环来固定矩形的边界,并在矩形的边界中找出最小的高度。这样的操作总的时间复杂度为 O ( n 2 ) O(n^2) O(n2), n n n 为数组 heights 的高度,对于本题 1 0 5 10^5 105 的数据规模,一定超时。
如果我们枚举「高」,需要将数组 heights 中的每一个高度 heights[i] 作为矩形的高,并在这个高度左侧和右侧分别找到 最近的高度小于 heights[i] 的柱子,这两个柱子之间(不包括本身)的所有柱子高度均小于 heights,就是 i 能扩展的最远距离。 这样操作总的时间复杂度为 O ( n 2 ) O(n^2) O(n2),也会超时。
方法二:单调栈
思路
方法二就是将方法一种枚举「高」当中的找到 “最近的高度小于 heights[i] 的柱子” 利用单调栈的方法先计算出来,从来降低时间复杂度。
维护两个数组 left 和 right,left[i] 和 right[i] 分别表示柱子 i 左侧且最近的小于其高度的柱子和柱子 i 右侧且最近的小于其高度的柱子。这样以 heighet[i] 为高度的矩形宽度为
r i g h t [ i ] − 1 − ( l e f t [ i ] + 1 ) + 1 = r i g h t [ i ] − l e f t [ i ] − 1 right[i] - 1 - (left[i] + 1) + 1 = right[i] - left[i] - 1 right[i]−1−(left[i]+1)+1=right[i]−left[i]−1
首先定义一个单调栈 mono_stack 用来存放柱子在数组中的位置,接着从前往后枚举数组 heights 来更新 left 以及单调栈 mono_stack:
- 将栈顶的元素与当前枚举的元素值 heights[i] 比较,如果栈非空并且栈顶的元素值大于或者等于 heights[i],就出栈,直到栈为空或者找到比 heights[i] 小的栈中元素;
- 如果栈为空了,说明 heights[i] 左侧没有比它小的元素,更新left[i] = -1;否则就是找到了heights[i] 左侧比它小的元素;
- 将 nums2[i] 加入栈中。
按照以上操作可以计算出数组 left,同理可以得到 right。
最后,依次枚举数组 heights 中的高度,计算以每个高度为矩形的高的最大值。因为题目要求 “好子数组中间必须包含下标 k”,即矩形必须包含下标 k,于是需要增加一条判断:left[i] < k && k < right[i],在该条件成立的情况下,计算矩形的最大面积,即本题的好子数组的最大可能分数。
实现代码
class Solution {
public:int maximumScore(vector<int>& heights, int k) {int n = heights.size();vector<int> left(n), right(n);stack<int> mono_stack;for (int i = 0; i < n; ++i) {while (!mono_stack.empty() && heights[mono_stack.top()] >= heights[i]) {mono_stack.pop();}left[i] = mono_stack.empty() ? -1 : mono_stack.top();mono_stack.push(i);}mono_stack = stack<int>();for (int i = n-1; i >= 0; --i) {while(!mono_stack.empty() && heights[mono_stack.top()] >= heights[i]) {mono_stack.pop();}right[i] = mono_stack.empty() ? n : mono_stack.top();mono_stack.push(i);}int res = 0;for (int i = 0; i < n; ++i) {if (left[i] < k && k < right[i])res = max(res, (right[i] - left[i] - 1) * heights[i]);}return res;}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n), n n n 为数组 heights 的高度。
空间复杂度: O ( n ) O(n) O(n)。
写在最后
如果您发现文章有任何错误或者对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度的方法,欢迎评论区交流。
最后,感谢您的阅读,如果有所收获的话可以给我点一个 👍 哦。
相关文章:

【每日一题】好子数组的最大分数
Tag 【单调栈】【暴力枚举】【数组】【2024-03-19】 题目来源 1793. 好子数组的最大分数 解题思路 本题和 84. 柱状图中最大的矩形 一样,计算的都是最大矩形的面积。只不过多了一个约束:矩形必须包含下标 k。 以下的方法一和方法二是 84. 柱状图中最…...
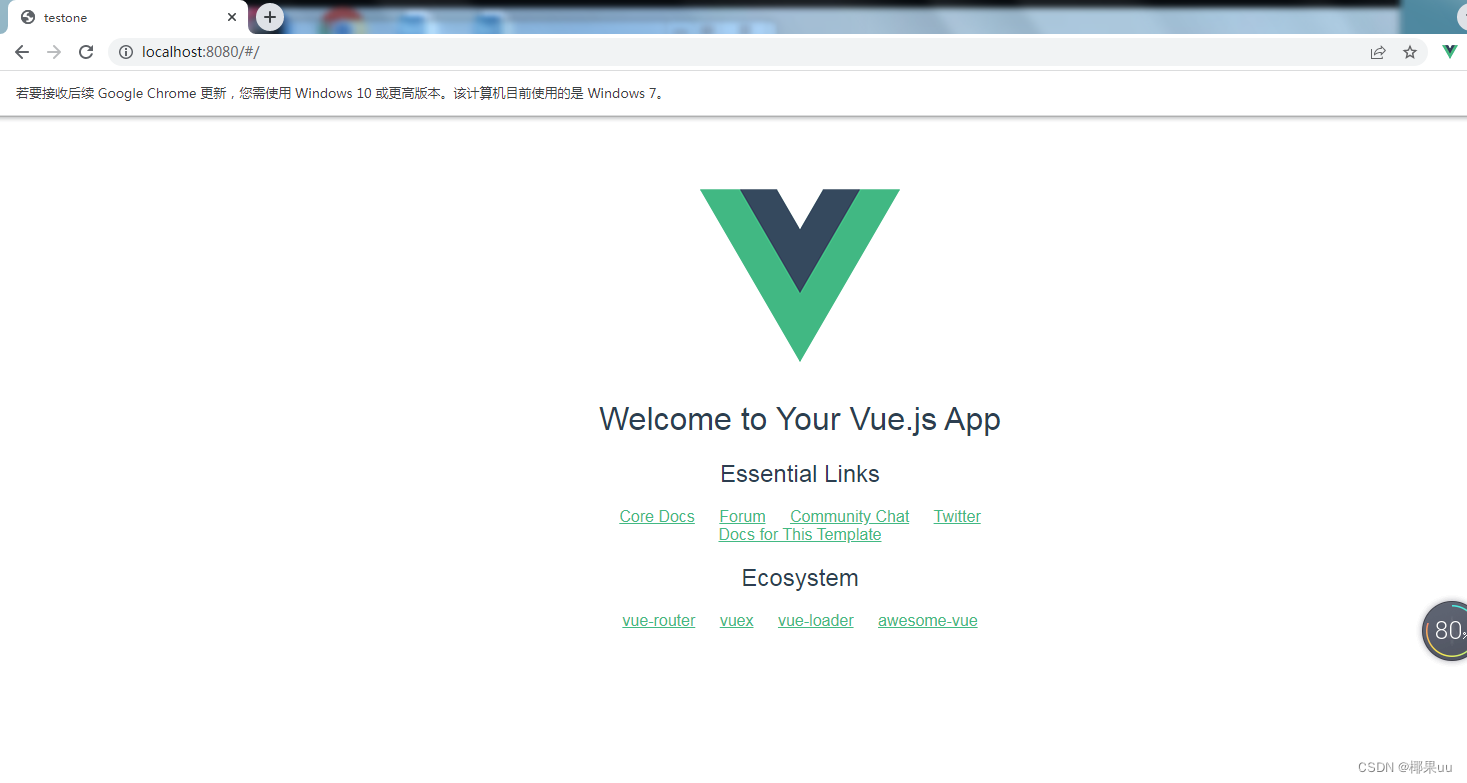
Vue2(七):超详细vue开发环境搭建(win7),nodejs下载与安装,安装淘宝镜像(报错已解决),配置脚手架
一、安装node.js 本来想粗略写一下的,但是搭建脚手架的时候,遇到了很多问题,浪费快两天时间,记录一下自己的解决办法希望对你们有帮助! 1.下载nodejs 安装包下载链接【CNPM Binaries Mirror】 下载我划线的这个&am…...
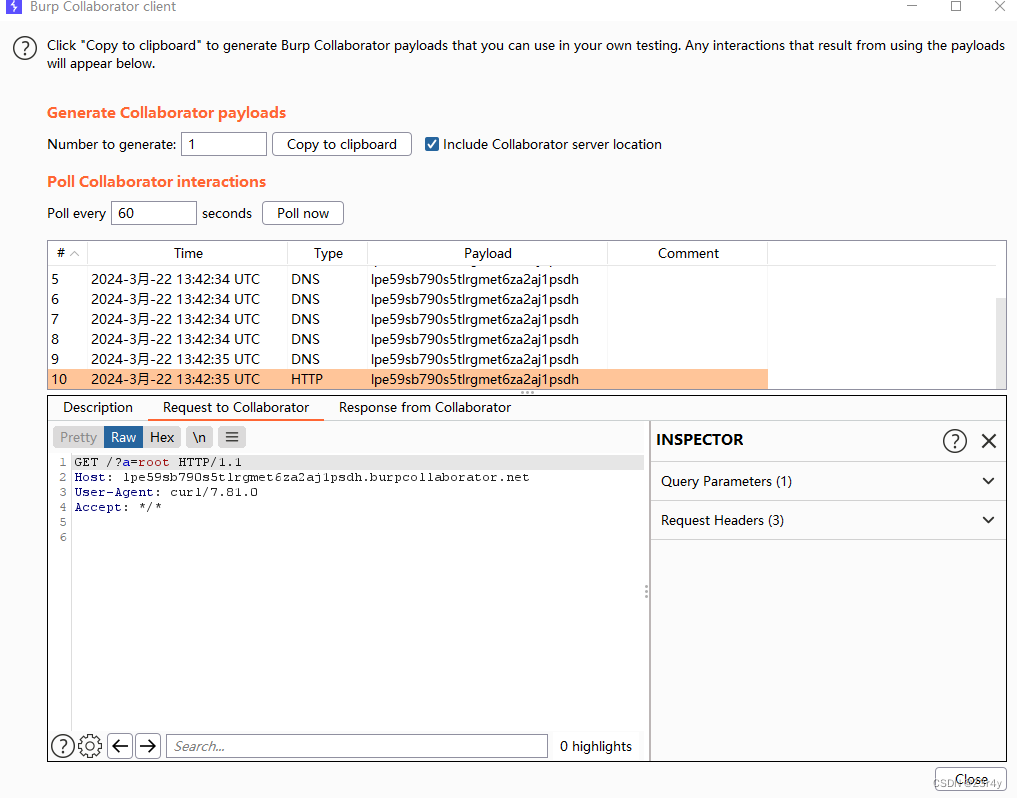
【Web】记录CISCN 2021 总决赛 ezj4va题目复现——AspectJWeaver
目录 前言 原理分析 step 0 step 1 EXP 前文:【Web】浅聊Java反序列化之AspectJWeaver——任意文件写入-CSDN博客 前言 这就是当年传说中的零解题嘛😭,快做🤮了 有了之前的经验,思路顺挺快的,中间不…...
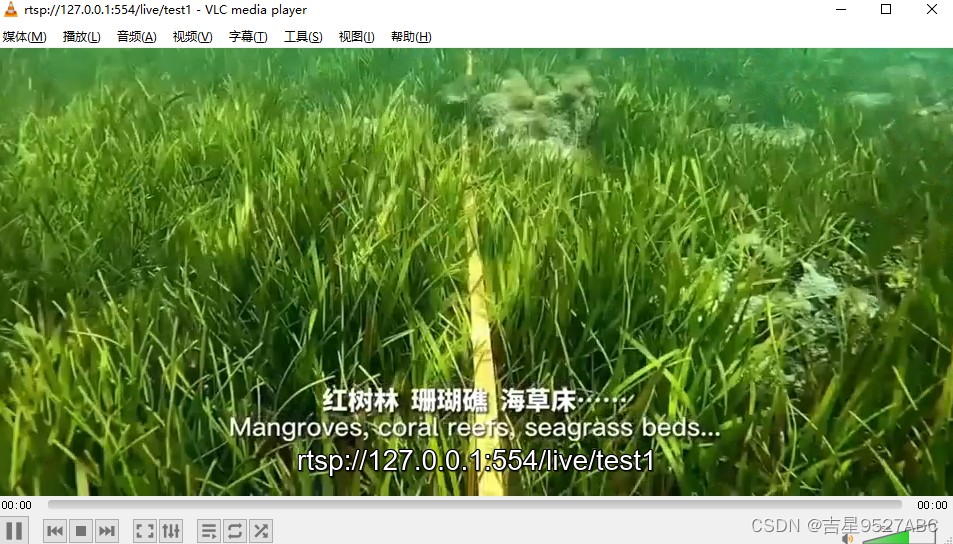
视频技术1:使用ABLMediaServer推流rtsp
ABLMediaServer定位是高性能、高稳定、开箱即用、商用级别的流媒体服务器 下边展示了如何把1个mp3作为输入源,转换为rtsp流的过程。 作用:用rtsp模拟摄像头的视频流 1、启动ABLMediaServer ABLMediaServer-2024-03-13\WinX64\ABLMediaServer.exe 配…...

HTML5+CSS3+JS小实例:创意罗盘时钟
实例:创意罗盘时钟 技术栈:HTML+CSS+JS 效果: 源码: 【HTML】 <!DOCTYPE html> <html lang="zh-CN"><head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=…...

设计数据库之内部模式:SQL基本操作
Chapter4:设计数据库之内部模式:SQL基本操作 笔记来源: 1.《漫画数据库》—科学出版社 2.SQL | DDL, DQL, DML, DCL and TCL Commands 设计数据库的步骤: 概念模式 概念模式(conceptual schema)是指将现实世界模型化的阶段进而&…...
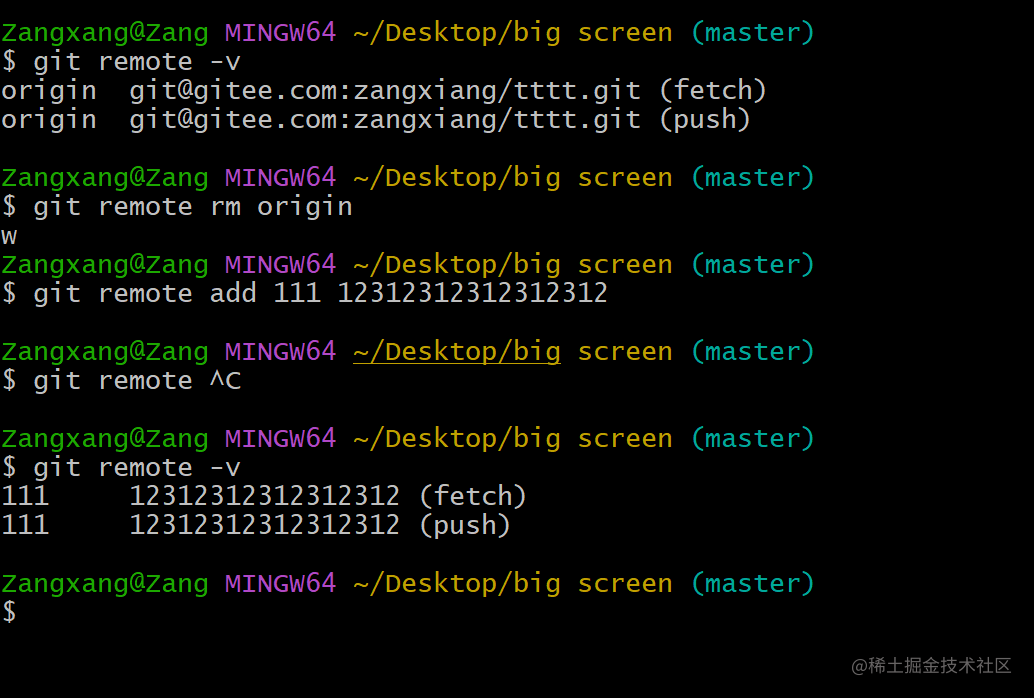
Git浅谈配置文件和免密登录
一、文章内容 简述git三种配置ssh免密登录以及遇见的问题git可忽略文件git remote 相关操作 二、Git三种配置 项目配置文件(局部):项目路径/.git/config 文件 git config --local user.name name git config --local user.email 123qq.cc全局配置文(所有用户): …...

【好玩的经典游戏】Docker环境下部署RPG网页小游戏
【好玩的经典游戏】Docker环境下部署RPG网页小游戏 一、react-tetris小游戏介绍1.1 react-tetris小游戏简介1.2 项目预览二、本次实践介绍2.1 本地环境规划2.2 本次实践介绍三、本地环境检查3.1 安装Docker环境3.2 检查Docker服务状态3.3 检查Docker版本3.4 检查docker compose…...

前端逻辑错误或UI崩溃解决问题
全屏错误覆盖层或UI崩溃 VueReact(错误边界) Vue Vue的全屏错误覆盖层解决,其实只需要配置Error就好,在开发服务器的client.overlay中设置关闭全屏覆盖层 module.exports {devServer: {client: {overlay: {warnings: false,error…...
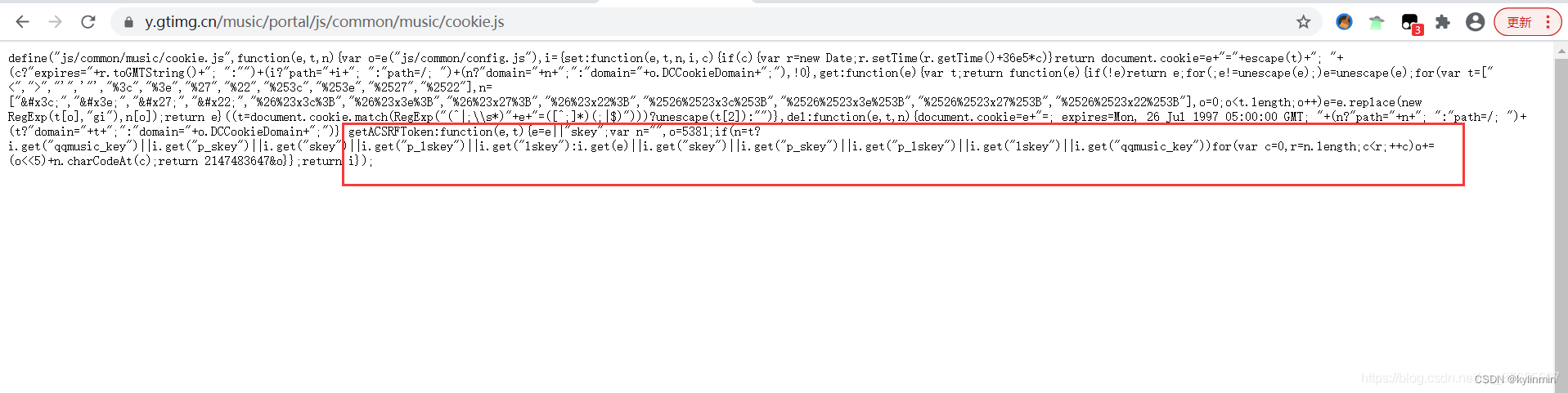
python爬取QQ音乐评论信息
python爬取QQ音乐评论信息 python爬取QQ音乐评论信息1.随便选个音乐python爬取QQ音乐评论信息 1.随便选个音乐 https://y.qq.com/n/yqq/song/0039MnYb0qxYhV.html 当前的后台调试页面显示如下: 找到评论的数据接口: https://c.y.qq.com/base/fcgi-bin/fcg_global_comme…...
——SBP介绍)
Unity构建详解(1)——SBP介绍
【前言】 Unity的资源工作流程分为导入、创建、构建、分发、加载。我们说的是其中的构建步骤。 构建是指将项目工程中的资源文件和代码整合程可执行文件的过程,构建的结果是生成可执行文件,在win平台上是exe,在Android平台上是apkÿ…...
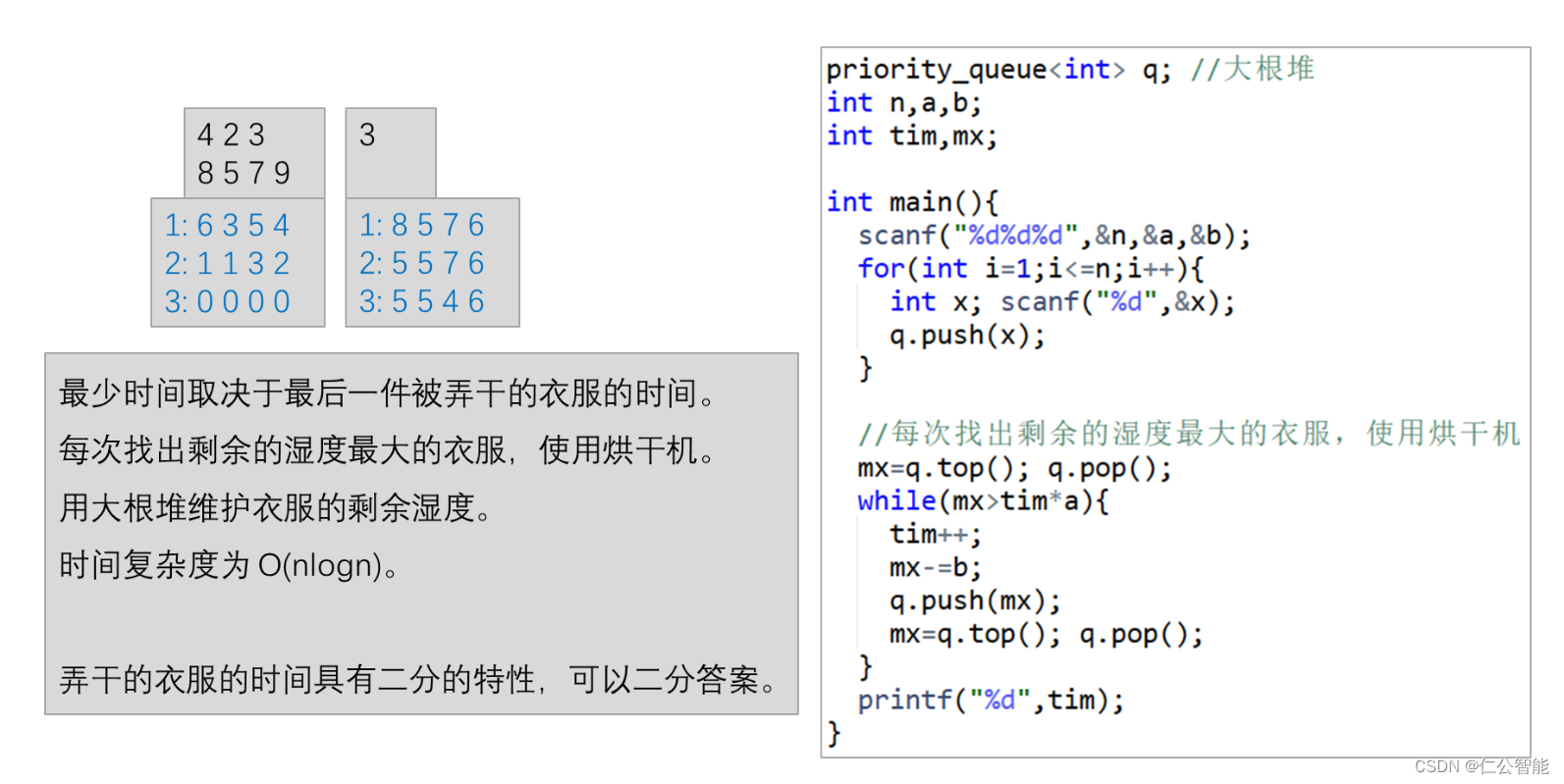
贪心算法(算法竞赛、蓝桥杯)--奶牛晒衣服
1、B站视频链接:A28 贪心算法 P1843 奶牛晒衣服_哔哩哔哩_bilibili 题目链接:奶牛晒衣服 - 洛谷 #include <bits/stdc.h> using namespace std; priority_queue<int> q;//用大根堆维护湿度的最大值 int n,a,b; int tim,maxn;int main(){s…...

Redis列表:高效消息通信与实时数据处理的利器
Redis是一个强大的开源内存数据库,被广泛应用于缓存、会话存储、队列等各种场景中。在Redis中,列表(List)是一种非常重要的数据结构,它提供了存储、获取、操作有序元素集合的功能。本文将深入探讨Redis列表的特性、使用…...
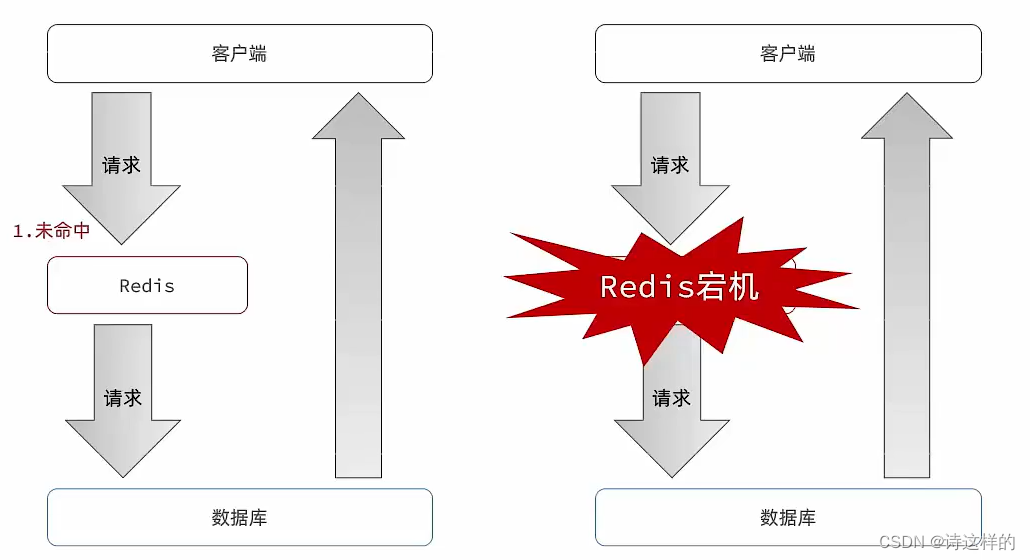
Redis中的缓存雪崩
缓存雪崩 🤔现象分析 缓存雪崩是指在同一时段大量的缓存key同时失效或者缓存服务(Redis等)宕机,导致大量请求到达数据库,带来巨大压力。 👊 解决方案 利用Redis集群提高服务的可用性,避免缓存服务宕机给缓存业务添…...
使用远程工具连接Mysql
(若想要远程连接Mysql需要下面解决四个问题) 1、目标地址 直接查询 2、端口号 3306 3、防火墙关闭 [rootlocalhost date]# systemctl stop firewalld.service 4、授权mysql数据库root用户权限(因为mysql开始不允许其他IP访问࿰…...

2024不起眼的“致富”野路子,不想打工了,做做这些暴利创业项目。2024个人创业做什么项目好;最适合白手起家的创业项目
经济大环境差,并不代表就没有机会。相反,主流经济不好正是另一些人所看重的千载难逢的机会。就像股票市场一样,有人靠做多赚钱,有人靠做空赚钱。下面我们就来分析一下哪些行业会在这个时候崛起。 首先二手行业会迅速崛起ÿ…...
从后端获取文件数据并导出
导出文件的公共方法 export const download (res, tools) > {const { message, hide } tools;const fileReader: any new FileReader();console.log(fileReader-res>>>, res);fileReader.onload (e) > {if (res?.data?.type application/json) {try {co…...

哲♂学家带你深♂入了♂解结构体及结构体内存大小问题
目录 概要 一、结构体的声明 二、结构体变量的创建和初始化 三、结构体的特殊声明 四、结构体内存对齐 1、对齐原则 2、例一 对齐数 计算方法 3、例二 总结 概要 结构体是我们日常编程中经常要用到的一种自定义类型,使用起来也是十分的方便。接下来就由…...
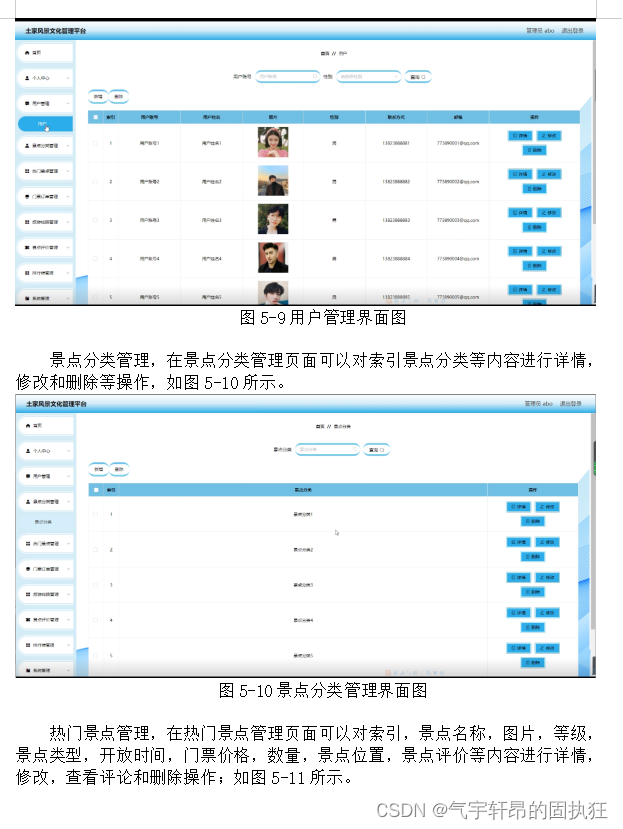
基于SSM的土家风景文化管理平台(有报告)。Javaee项目。ssm项目。
演示视频: 基于SSM的土家风景文化管理平台(有报告)。Javaee项目。ssm项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构,通过Spri…...

2024年03月CCF-GESP编程能力等级认证C++编程一级真题解析
本文收录于专栏《C++等级认证CCF-GESP真题解析》,专栏总目录:点这里。订阅后可阅读专栏内所有文章。 一、单选题(每题 2 分,共 30 分) 第 1 题 C++表达式 (3 - 2) * 3 + 5 的值是( )。 A. -13 B. 8 C. 2 D. 0 答案:B 第 2 题 C++语句 cout << “5%2=” <&l…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...
