[ABC206E] Divide Both 解题记录
[ABC206E] Divide Both 解题记录
题意简述
给定整数 L , R L,R L,R,求满足以下条件的数对 ( x , y ) (x,y) (x,y) 的数量。
- x , y x,y x,y 不互质
- x ∤ y x \nmid y x∤y 且 y ∤ x y \nmid x y∤x
题目分析
正难则反,考虑用所有的满足第一条性质的数对的数量减去不满足第二条性质的数量。
容易想到,如果不考虑第二条性质,那么我们可以枚举因子 i ∈ [ 2 , r ] i \in [2,r] i∈[2,r],求解出 [ l , r ] [l,r] [l,r] 区间内的 i i i 的倍数的个数 s s s,然后用加法原理,两两配对,累加到答案中。
如何求解 s s s?
不妨设 x = k × i + b x=k \times i+b x=k×i+b,则 i ∣ ( x − b ) i \mid (x-b) i∣(x−b),即对于每个 j ∈ [ 1 , k ] j \in [1,k] j∈[1,k] 都有 i ∣ ( x − b − j × i ) i \mid (x-b-j \times i) i∣(x−b−j×i),一共 k k k 个数,而这个 k k k 就是 ⌊ r i ⌋ \lfloor\frac{r}{i}\rfloor ⌊ir⌋,对于 k k k 个数字两两配对,即可求解出 s = k × ( k − 1 ) 2 s=\frac{k \times (k-1)}{2} s=2k×(k−1)。但是这样会有重复,如:当 i = 2 , 3 , 6 i=2,3,6 i=2,3,6 时,均会有数对 ( 6 , 12 ) (6,12) (6,12),这个时候就需要我们标记了。可以设 c n t i cnt_i cnti 表示 i i i 的质因子的个数,如果 c n t i cnt_i cnti 为偶数,就减去当前贡献,否则加上。那么我们对于 i = 2 , 3 i=2,3 i=2,3 的时候加上了 ( 6 , 12 ) (6,12) (6,12) 的贡献,在 i = 6 i=6 i=6 的时候就会减去一个,这样就保证了贡献不会重复(不清楚的可以手模)。
最后减去不满足第二条限制的贡献:对于每个因子 i ∈ [ 2 , r ] i \in [2,r] i∈[2,r],减去 [ l , r ] [l,r] [l,r] 中除 i i i 外 i i i 的倍数,即: ⌊ r i ⌋ − 1 \lfloor\frac{r}{i}\rfloor -1 ⌊ir⌋−1。
AC Code
#include<bits/stdc++.h>
#define arrout(a,n) rep(i,1,n)std::cout<<a[i]<<" "
#define arrin(a,n) rep(i,1,n)std::cin>>a[i]
#define rep(i,x,n) for(int i=x;i<=n;i++)
#define dep(i,x,n) for(int i=x;i>=n;i--)
#define erg(i,x) for(int i=head[x];i;i=e[i].nex)
#define dbg(x) std::cout<<#x<<":"<<x<<" "
#define mem(a,x) memset(a,x,sizeof a)
#define all(x) x.begin(),x.end()
#define arrall(a,n) a+1,a+1+n
#define PII std::pair<int,int>
#define m_p std::make_pair
#define u_b upper_bound
#define l_b lower_bound
#define p_b push_back
#define CD const double
#define CI const int
#define int long long
#define il inline
#define ss second
#define ff first
#define itn int
CI N=1e6+5;
int l,r,ans,cnt[N];
void init() {rep(i,2,r) {if(cnt[i]!=0) {continue;}for(int j=i;j<=r;j+=i) {if(cnt[j]>=0) {cnt[j]++;}}for(int j=i*i;j<=r;j+=i*i) {cnt[j]=-1;}}
}
signed main() {std::cin>>l>>r;init();rep(i,2,r) {if(cnt[i]<0) {continue;}int s=r/i-(l-1)/i;s=s*(s-1)/2;if(cnt[i]%2) {ans+=s;} else {ans-=s;}}rep(i,std::max(l,2ll),r) {ans-=r/i-1;}std::cout<<ans*2;return 0;
}
相关文章:

[ABC206E] Divide Both 解题记录
[ABC206E] Divide Both 解题记录 题意简述 给定整数 L , R L,R L,R,求满足以下条件的数对 ( x , y ) (x,y) (x,y) 的数量。 x , y x,y x,y 不互质 x ∤ y x \nmid y x∤y 且 y ∤ x y \nmid x y∤x 题目分析 正难则反,考虑用所有的满足第一条性质的…...

常见的服务器技术和服务器技术的重要性
服务器技术是指一系列用于构建、维护和管理服务器的技术和工具,旨在确保服务器能够高效、稳定、安全地运行,以满足客户端的请求并提供各种服务。它涵盖了服务器硬件、操作系统、网络协议、数据存储和安全等多个方面的知识和技能。今天,德迅云…...
MATLAB中的数学建模:基础知识、实例与方法论
前言 在当今科技高速发展的时代,数学建模成为了解析复杂世界的关键工具,而MATLAB作为一种专业的科学计算软件,为我们提供了强大的数学建模平台。MATLAB不仅仅是Matrix Laboratory的简称,更是一个集数值分析、矩阵计算、算法开发和…...

Flutter与Xamarin跨平台APP开发框架的区别
嘿,各位亲爱的朋友们!大家好,我是咕噜铁蛋!今天我们要探讨的话题是:Flutter与Xamarin这两款热门的跨平台APP开发框架。我深知选择合适的开发工具对于开发者来说有多么重要。那么,当我们需要开发跨平台应用时…...

【JAVA】Springboot集成Proguard完成jar包混淆
目录 一、需求背景 二、具体实现 一、需求背景 某些情况下需要将jar包交付给第三方,担心第三方会将代码进行反编译,故需要将jar包进行处理。 jar包源码混淆工具有多种,但真正能投入使用的产品并不多。 比如 ClassFinal (ClassFinal: Jav…...
全流程ArcGIS Pro技术应用
GIS是利用电子计算机及其外部设备,采集、存储、分析和描述整个或部分地球表面与空间信息系统。简单地讲,它是在一定的地域内,将地理空间信息和 一些与该地域地理信息相关的属性信息结合起来,达到对地理和属性信息的综合管理。GIS的…...

4.windows ubuntu 子系统:微生物宏基因组测序和分析流程概括。
微生物宏基因组测序和分析流程大致可以分为以下几个步骤: DNA提取:需要从微生物样本中提取DNA。2.建库构建:提取到的DNA需要进行建库构建,包括DNA片段的断裂、末端修复、连接连接适配器等操作。3.高通量测序:建库构建完…...
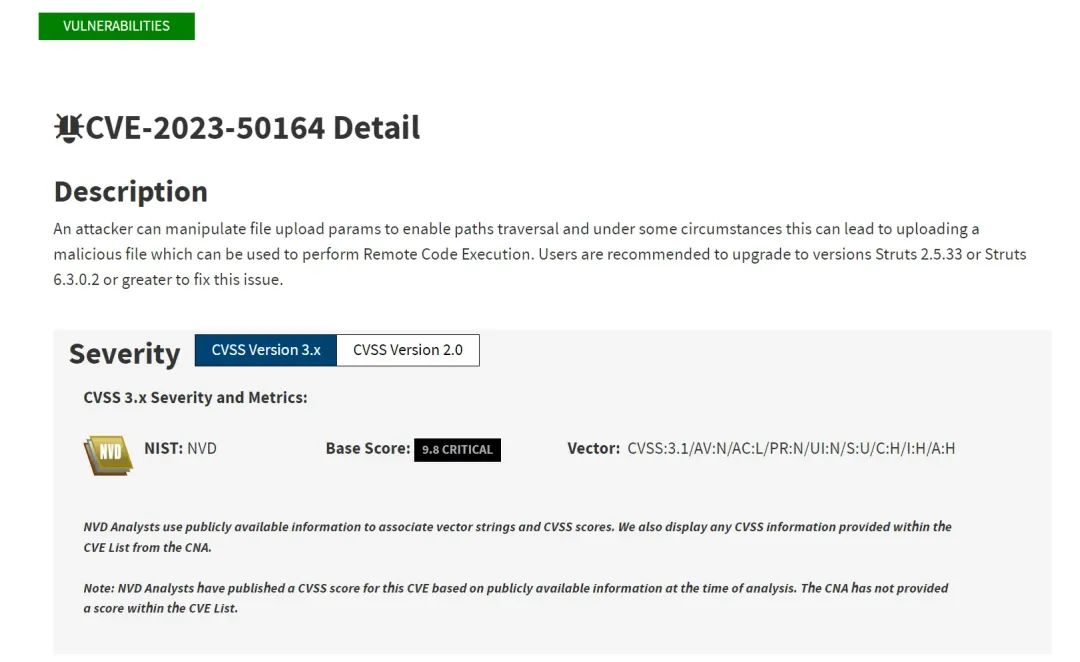
S2-066分析与复现
Foreword 自struts2官方纰漏S2-066漏洞已经有一段时间,期间断断续续地写,直到最近才完成,o(╥﹏╥)o。羞愧地回顾一下官方通告: 2023.12.9发布,编号CVE-2023-50164,主要影响版本是 2.5.0-2.5.32 以及 6.0.…...

让天下没有难学的大模型!我整理一份大模型技术知识图谱!
最近陆续有一些同学反馈,感觉大模型知识点太多了,找不到头绪。 今天我整理一份大模型技术以及应用的知识图谱,让大家轻松学习大模型,喜欢点赞、收藏、关注。 另外,技术交流可以文末加入我们。 大模型的预训练技术 …...

大屏动效合集更更更之实现百分比环形
实现效果 参考链接: https://pslkzs.com/demo/pie/demo1.php 写在最后🍒 源码,关注🍥苏苏的bug,🍡苏苏的github,🍪苏苏的码云...

基于springboot的反诈宣传平台
技术:springbootmysqlvue 一、系统背景 反欺诈平台可以对公交信息进行集中管理,可以真正避免传统管理的缺陷。反欺诈平台是一款运用软件开发技术设计实现的应用系统,在信息处理上可以达到快速的目的,不管是针对数据添加ÿ…...

面试算法-82-不同路径
题目 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 问总共有多少条不同的路径? …...
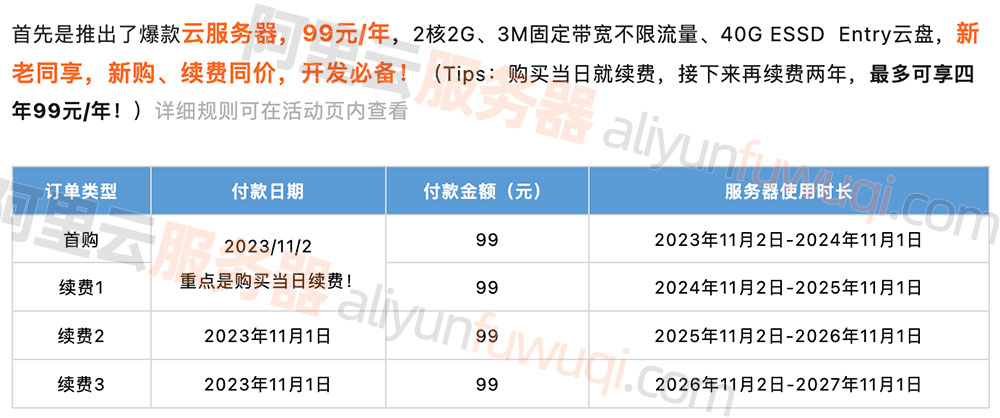
阿里云ECS经济型e实例,2核2G配置、3M固定带宽和40G ESSD Entry系统盘
阿里云服务器99元一年配置为云服务器ECS经济型e实例,2核2G配置、3M固定带宽和40G ESSD Entry系统盘,新用户和老用户均可买,续费不涨价依旧是99元一年,阿里云服务器网aliyunfuwuqi.com来详细说下阿里云99元服务器性能测评ÿ…...
)
Java基础知识总结(13)
数据结构 链表 优点:随机增删元素效率高(因为增删元素不涉及到大量元素的位移) 缺点:查询效率较低,每一次查找某个元素的时候都需要从头结点开始往下遍历 LinkedList集合 /* 链表的优点: 由于链表的元…...
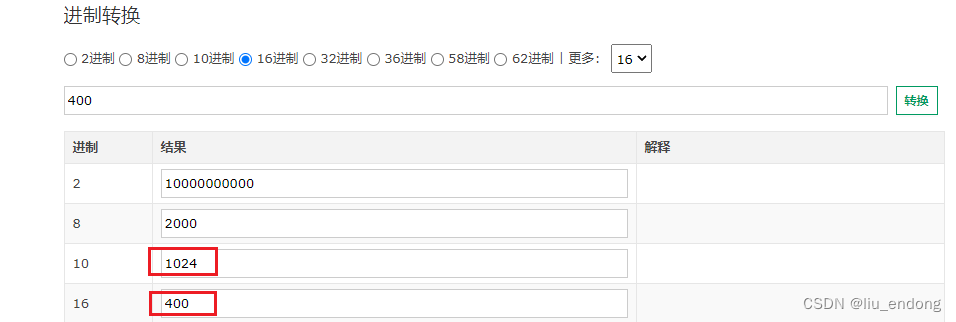
杰发科技AC7801——Keil编译的Hex大小如何计算
编译结果是Keil里面前三个数据的总和: 即CodeRoDataRWData的总和。 通过ATCLinkTool工具查看内存,发现最后一个字节正好是5328 注意读内存数据时候需要强转成32位,加1000的 增加1024的地址只需要加256即可...
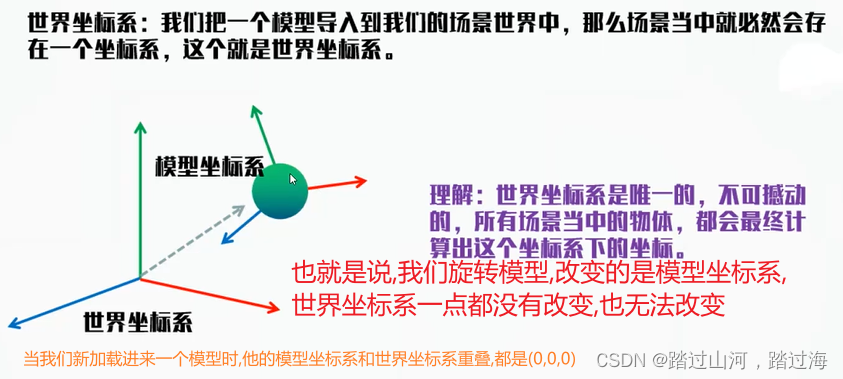
opengl 学习(六)-----坐标系统与摄像机
坐标系统与摄像机 分类引言坐标系统摄像机教程在CMake中使用全局定义预编译宏,来控制是否开启错误检查补充 分类 opengl c 引言 OpenGL希望在每次顶点着色器运行后,我们可见的所有顶点都为标准化设备坐标(Normalized Device Coordinate, NDC)。也就是说ÿ…...
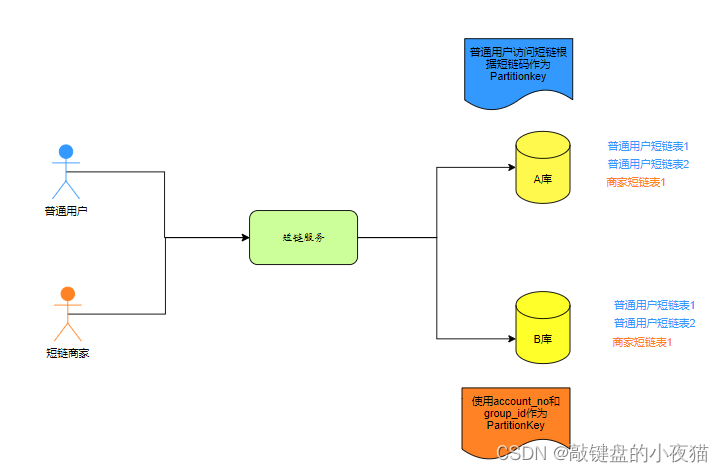
分库分表场景下多维查询解决方案(用户+商户)
在采用分库分表设计时,通过一个PartitionKey根据散列策略将数据分散到不同的库表中,从而有效降低海量数据下C端访问数据库的压力。这种方式可以缓解单一数据库的压力,提升了吞吐量,但同时也带来了新的问题。对于B端商户而言&#…...

vue学习日记14:工程化开发脚手架Vue CLI
一、概念 二、安装 1.全局安装&查看版本 注意启动cmd输入命令 要以管理员运行哦 安装了一次就行以后不用再创建了 yarn global addvue/cli vue --version 显示了版本号即可 2.创建项目架子 创建项目的路径在哪 项目就在哪 项目名字不能用中文 vue create project-n…...
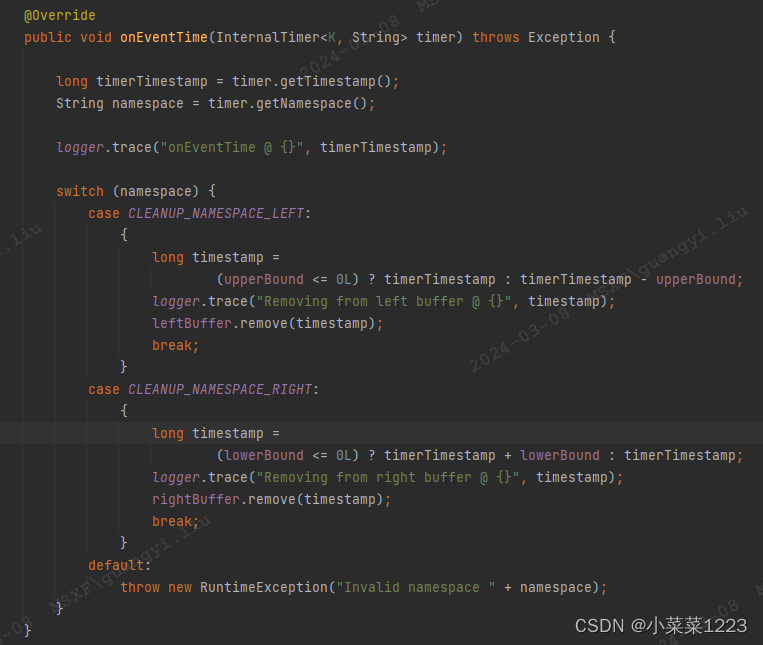
java Flink(四十三)Flink Interval Join源码解析以及简单实例
背景 之前我们在一片文章里简单介绍过Flink的多流合并算子 java Flink(三十六)Flink多流合并算子UNION、CONNECT、CoGroup、Join 今天我们通过Flink 1.14的源码对Flink的Interval Join进行深入的理解。 Interval Join不是两个窗口做关联,…...
JsonUtility.ToJson 和UnityWebRequest 踩过的坑记录
项目场景: 需求:我在做网络接口链接,使用的unity自带的 UnityWebRequest ,数据传输使用的json,json和自定义数据转化使用的也是unity自带的JsonUtility。使用过程中发现两个bug。 1.安全验证失败。 报错为:…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
