MATLAB中的数学建模:基础知识、实例与方法论
前言
在当今科技高速发展的时代,数学建模成为了解析复杂世界的关键工具,而MATLAB作为一种专业的科学计算软件,为我们提供了强大的数学建模平台。MATLAB不仅仅是Matrix Laboratory的简称,更是一个集数值分析、矩阵计算、算法开发和可视化于一体的软件环境。
数学建模的核心基础知识:MATLAB入门
数学建模的基础是对模型中使用的数学和物理概念的深入了解。在MATLAB中建模,首先要熟悉其环境。MATLAB的界面包括命令窗口、工作区、路径管理器和文件编辑器等几个主要部分,每一部分都为模型的开发和测试提供了便利。
数据和函数的基本操作
在MATLAB中,数据管理和函数的应用是编程的核心内容。为了充分利用MATLAB的强大功能进行数据分析和数学建模,必须掌握对数组和矩阵的基本操作以及编写和调用函数的方法。
数据操作
数组和矩阵的创建与操作:
矩阵是MATLAB中最基本的数据结构。操作矩阵的基础功能非常强大,可以涵盖从基础算术到复杂的数学运算。
示例代码:创建和转置矩阵
% 创建一个3x3的矩阵
A = [1, 2, 3; 4, 5, 6; 7, 8, 9];% 转置矩阵
A_transposed = A';
向量的创建与索引:
向量可以是行向量或列向量,并且在数学建模中经常用作数据集合或参数列表。
示例代码:创建等差向量并访问元素
% 创建一个包含从1到10的等差序列的向量,步长为0.1
v = 1:0.1:10;% 访问向量的第五个元素
fifth_element = v(5);
函数操作
函数定义与调用:
函数允许我们定义可重复使用的代码块,这在执行重复或标准计算时非常方便。
示例代码:定义一个计算圆的面积的函数
function area = calculateCircleArea(radius)% 计算圆的面积area = pi * radius^2;
end% 调用函数计算半径为5的圆的面积
circleArea = calculateCircleArea(5);
常用内置函数使用示例
MATLAB的一个重要特性是它提供的大量内置函数,能够覆盖不同领域的需求,从基本的数学运算到复杂的数据分析和工程计算。
数学函数
平方根、和、平均值计算:
这些常用的数学函数可以帮助我们快速对数据进行基本分析。
示例代码:使用内置函数处理向量
% 计算数字16的平方根
sqrt_result = sqrt(16);% 计算向量元素的和
vector_sum = sum([1, 2, 3, 4]);% 计算向量元素的平均值
vector_mean = mean([1, 2, 3, 4]);
数据分析函数
最大值、最小值和排序:
处理矩阵和向量时,常常需要找到最大值、最小值,或对数据进行排序。
示例代码:寻找向量的最大值和排序
% 创建向量
data_vector = [10, 3, 7, 5, 9, 1];% 找到向量中的最大值
[max_value, max_index] = max(data_vector);% 对向量进行升序排序
sorted_vector = sort(data_vector);数学建模的方法论:如何建模?
问题定义
数学建模启动于一个问题或研究课题。在科研中,明确你的目标和所需解答的问题是初步阶段。接下来,将实际问题抽象成数学问题,确定关键参数和边界条件。
模型的假设
您需要基于问题制定相应的假设来简化现实情况。例如,一个行星的运动模型通常会忽略非主要天体的影响,或者假设轨道为圆形而非椭圆。
数学工具和技巧的选择
依据问题的类型和建立的假设,决定使用代数、微积分、统计、几何或其他数学工具。例如,在动力系统分析中,微分方程是描述系统行为的主要工具。
MATLAB中的实例展示
我们通过一个太阳系简化模型来展示这个过程,当中,地球绕太阳公转的运动通过经典的二体问题来近似模拟。
下面的代码展示了如何在MATLAB中创建一个简化版的太阳系模型,其中只考虑太阳和地球。这个模型使用二体近似,在这个假设下,太阳可以被视为系统的中心,而地球绕它的运动轨迹可以通过牛顿的万有引力定律和运动方程来计算。
我们定义了地球与太阳之间的平均距离、地球的初始位置和速度向量,然后使用ode45这一MATLAB内置的常微分方程求解器来计算地球在一定时间跨度内的运动。
function solar_system_model% 定义了常数和初始条件G = 6.67430e-11; % 万有引力常数,m^3/kg/s^2M_sun = 1.989e30; % 太阳的质量,kgM_earth = 5.972e24; % 地球的质量,kgR = 1.496e11; % 地球和太阳之间平均距离,m% 地球绕太阳公转的角速度(简化为圆形轨道)omega = sqrt(G * M_sun / R^3);% 时间跨度:一年tspan = linspace(0, 2*pi/omega, 1000); % 分为1000个时间点% 初始位置和速度 [x0, y0, vx0, vy0]% 地球在x轴上,初始速度方向为y轴Y0 = [R, 0, 0, R * omega];% 使用ode45求解[t, Y] = ode45(@(t, y) two_body_equation(t, y, G, M_sun), tspan, Y0);% 画出轨道figure;plot(Y(:,1), Y(:,2));xlabel('x (m)');ylabel('y (m)');title('Earth orbit around the Sun using Two-Body Problem Simplification');axis equal;grid on;hold on;% 标记太阳的位置plot(0, 0, 'ro', 'MarkerSize', 15, 'MarkerFaceColor', 'r');
end% 本地函数 - 两体问题的微分方程
function dYdt = two_body_equation(t, Y, G, M_sun)% 提取位置和速度x = Y(1);y = Y(2);vx = Y(3);vy = Y(4);% 计算到太阳的距离r = sqrt(x^2 + y^2);% 根据万有引力定律计算加速度ax = -G * M_sun * x / r^3;ay = -G * M_sun * y / r^3;% 返回位置的导数(速度)和速度的导数(加速度)dYdt = [vx; vy; ax; ay];
end 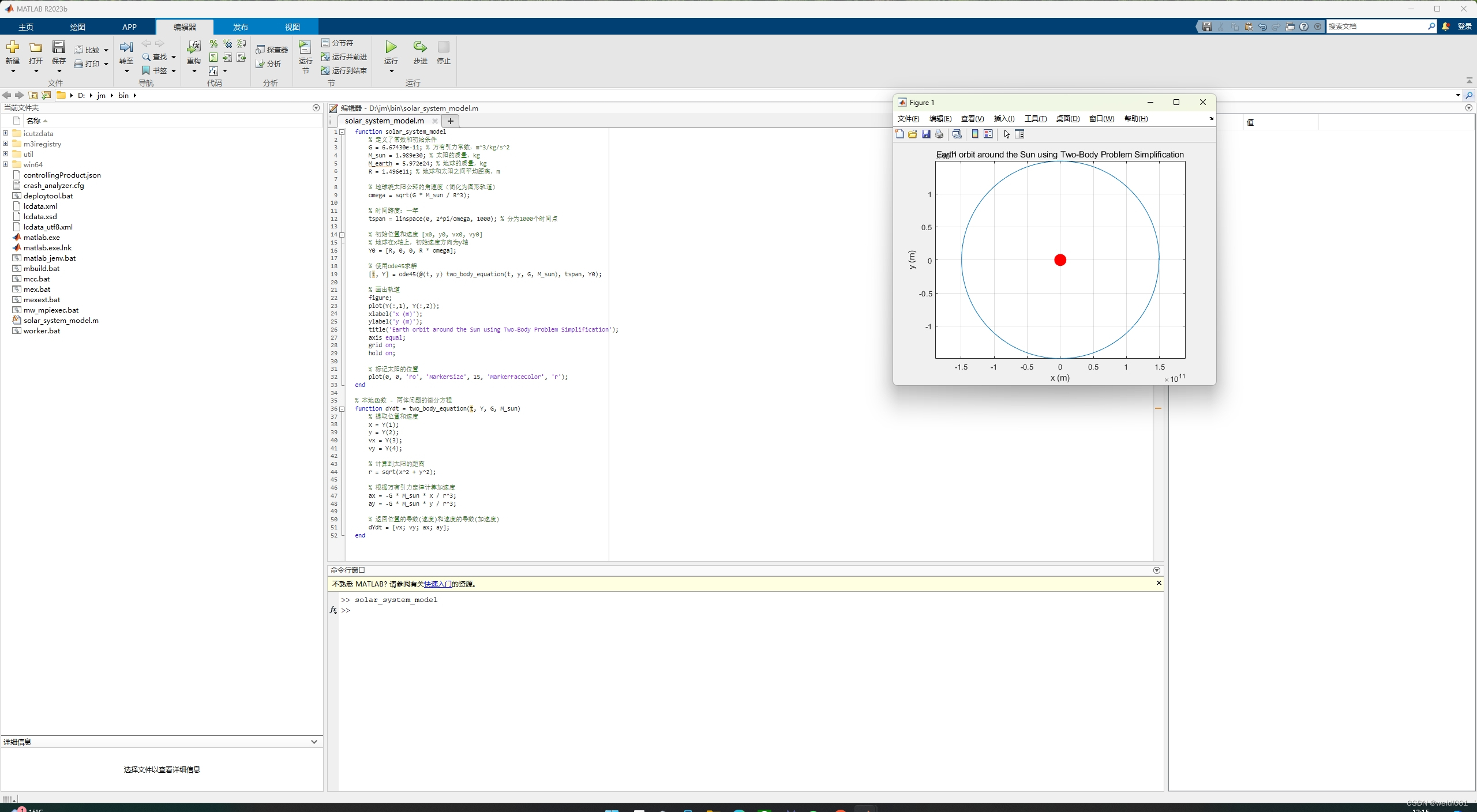
在这个模型中,我们使用的ode45求解器是基于Runge-Kutta方法的,适用于求解非刚性微分方程。它在科学和工程领域的数学建模中非常普遍,因为许多物理过程都可通过常微分方程进行描述。
此模型的输出是绘制了地球在一年内绕太阳运行的轨迹图。它非常直观地展示了MATLAB在数学建模方面的可视化和计算能力。
结论
MATLAB提供了一个用户友好、功能强大的环境,使数学建模既便捷又精确。它允许用户从最简单的线性模型到最复杂的动态系统模型,覆盖各种数学建模的需求。无论是学术研究还是工程实践,MATLAB都不可或缺。通过掌握编程和算法开发技能,并深入理解研究领域的数学和物理原理,学习和实践是发挥MATLAB全部潜力的关键。
附:进阶模型
function solar_system_model% 定义太阳的质量和万有引力常数G = 6.67430e-11; % m^3/kg/s^2M_sun = 1.989e30; % kg% (此处省略了前面已经提供的定义行星质量的代码)% 定义行星的初始位置和速度(以下的位置和速度数据应从天文资料获取精确值)% 地球R_earth = 1.496e11; % mV_earth = 29.78e3; % m/s% 水星 MercuryR_mercury = 5.79e10; % mV_mercury = 47.87e3; % m/s% 金星 VenusR_venus = 1.082e11; % mV_venus = 35.02e3; % m/s% 火星 MarsR_mars = 2.279e11; % mV_mars = 24.07e3; % m/s% 考虑椭圆轨道,初始化位置需要调整,以下是简化的圆形轨道% 时间跨度:一年,足够长以观察行星运动tspan = [0, 365*24*3600]; % 以秒为单位% 初始化位置和速度向量(此处省略初始化其他行星的代码)% 初始时刻假设所有行星都在太阳的右侧,并沿着y轴方向运动init_conditions = [R_mercury, 0, 0, V_mercury, % 水星R_venus, 0, 0, V_venus, % 金星R_earth, 0, 0, V_earth, % 地球R_mars, 0, 0, V_mars, % 火星% 为木星、土星、天王星、海王星添加初始条件...];% 使用ode45求解器进行数值积分options = odeset('RelTol', 1e-5, 'AbsTol', 1e-6);[t, Y] = ode45(@(t, y) n_body_problem(t, y, G, M_sun, M_mercury, M_venus, M_earth, M_mars), tspan, init_conditions, options);% 绘制位置和轨道的后续代码(此处省略)
end% N体问题的微分方程
function dYdt = n_body_problem(t, Y, G, M_sun, M_mercury, M_venus, M_earth, M_mars)% 提取各个行星的位置和速度x_mercury = Y(1); y_mercury = Y(2); vx_mercury = Y(3); vy_mercury = Y(4);x_venus = Y(5); y_venus = Y(6); vx_venus = Y(7); vy_venus = Y(8);x_earth = Y(9); y_earth = Y(10); vx_earth = Y(11); vy_earth = Y(12);x_mars = Y(13); y_mars = Y(14); vx_mars = Y(15); vy_mars = Y(16);% 为木星、土星、天王星、海王星添加位置和速度变量...% 计算太阳对每个行星的引力作用% 对于水星Mercuryr_mercury = sqrt(x_mercury^2 + y_mercury^2);ax_mercury = -G * M_sun * x_mercury / r_mercury^3;ay_mercury = -G * M_sun * y_mercury / r_mercury^3;% 对于金星Venusr_venus = sqrt(x_venus^2 + y_venus^2);ax_venus = -G * M_sun * x_venus / r_venus^3;ay_venus = -G * M_sun * y_venus / r_venus^3;% 对于地球Earthr_earth = sqrt(x_earth^2 + y_earth^2);ax_earth = -G * M_sun * x_earth / r_earth^3;ay_earth = -G * M_sun * y_earth / r_earth^3;% 对于火星Marsr_mars = sqrt(x_mars^2 + y_mars^2);ax_mars = -G * M_sun * x_mars / r_mars^3;ay_mars = -G * M_sun * y_mars / r_mars^3;% 为木星、土星、天王星、海王星添加加速度计算...% 计算行星间的引力作用(略)% 将速度和加速度组合成导数向量返回dYdt = [vx_mercury; vy_mercury; ax_mercury; ay_mercury;vx_venus; vy_venus; ax_venus; ay_venus;vx_earth; vy_earth; ax_earth; ay_earth;vx_mars; vy_mars; ax_mars; ay_mars;% 为木星、土星、天王星、海王星添加导数...];
end相关文章:

MATLAB中的数学建模:基础知识、实例与方法论
前言 在当今科技高速发展的时代,数学建模成为了解析复杂世界的关键工具,而MATLAB作为一种专业的科学计算软件,为我们提供了强大的数学建模平台。MATLAB不仅仅是Matrix Laboratory的简称,更是一个集数值分析、矩阵计算、算法开发和…...

Flutter与Xamarin跨平台APP开发框架的区别
嘿,各位亲爱的朋友们!大家好,我是咕噜铁蛋!今天我们要探讨的话题是:Flutter与Xamarin这两款热门的跨平台APP开发框架。我深知选择合适的开发工具对于开发者来说有多么重要。那么,当我们需要开发跨平台应用时…...

【JAVA】Springboot集成Proguard完成jar包混淆
目录 一、需求背景 二、具体实现 一、需求背景 某些情况下需要将jar包交付给第三方,担心第三方会将代码进行反编译,故需要将jar包进行处理。 jar包源码混淆工具有多种,但真正能投入使用的产品并不多。 比如 ClassFinal (ClassFinal: Jav…...
全流程ArcGIS Pro技术应用
GIS是利用电子计算机及其外部设备,采集、存储、分析和描述整个或部分地球表面与空间信息系统。简单地讲,它是在一定的地域内,将地理空间信息和 一些与该地域地理信息相关的属性信息结合起来,达到对地理和属性信息的综合管理。GIS的…...

4.windows ubuntu 子系统:微生物宏基因组测序和分析流程概括。
微生物宏基因组测序和分析流程大致可以分为以下几个步骤: DNA提取:需要从微生物样本中提取DNA。2.建库构建:提取到的DNA需要进行建库构建,包括DNA片段的断裂、末端修复、连接连接适配器等操作。3.高通量测序:建库构建完…...
S2-066分析与复现
Foreword 自struts2官方纰漏S2-066漏洞已经有一段时间,期间断断续续地写,直到最近才完成,o(╥﹏╥)o。羞愧地回顾一下官方通告: 2023.12.9发布,编号CVE-2023-50164,主要影响版本是 2.5.0-2.5.32 以及 6.0.…...

让天下没有难学的大模型!我整理一份大模型技术知识图谱!
最近陆续有一些同学反馈,感觉大模型知识点太多了,找不到头绪。 今天我整理一份大模型技术以及应用的知识图谱,让大家轻松学习大模型,喜欢点赞、收藏、关注。 另外,技术交流可以文末加入我们。 大模型的预训练技术 …...

大屏动效合集更更更之实现百分比环形
实现效果 参考链接: https://pslkzs.com/demo/pie/demo1.php 写在最后🍒 源码,关注🍥苏苏的bug,🍡苏苏的github,🍪苏苏的码云...

基于springboot的反诈宣传平台
技术:springbootmysqlvue 一、系统背景 反欺诈平台可以对公交信息进行集中管理,可以真正避免传统管理的缺陷。反欺诈平台是一款运用软件开发技术设计实现的应用系统,在信息处理上可以达到快速的目的,不管是针对数据添加ÿ…...

面试算法-82-不同路径
题目 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 问总共有多少条不同的路径? …...
阿里云ECS经济型e实例,2核2G配置、3M固定带宽和40G ESSD Entry系统盘
阿里云服务器99元一年配置为云服务器ECS经济型e实例,2核2G配置、3M固定带宽和40G ESSD Entry系统盘,新用户和老用户均可买,续费不涨价依旧是99元一年,阿里云服务器网aliyunfuwuqi.com来详细说下阿里云99元服务器性能测评ÿ…...
)
Java基础知识总结(13)
数据结构 链表 优点:随机增删元素效率高(因为增删元素不涉及到大量元素的位移) 缺点:查询效率较低,每一次查找某个元素的时候都需要从头结点开始往下遍历 LinkedList集合 /* 链表的优点: 由于链表的元…...
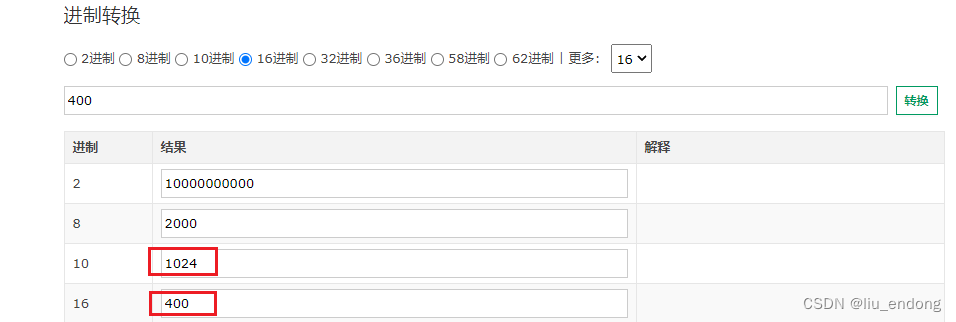
杰发科技AC7801——Keil编译的Hex大小如何计算
编译结果是Keil里面前三个数据的总和: 即CodeRoDataRWData的总和。 通过ATCLinkTool工具查看内存,发现最后一个字节正好是5328 注意读内存数据时候需要强转成32位,加1000的 增加1024的地址只需要加256即可...
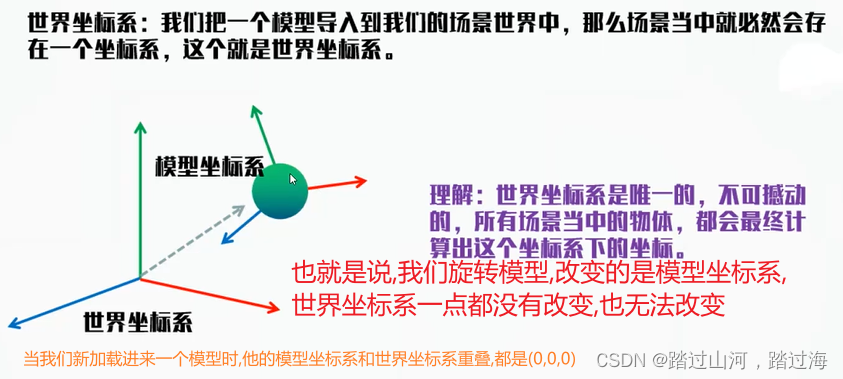
opengl 学习(六)-----坐标系统与摄像机
坐标系统与摄像机 分类引言坐标系统摄像机教程在CMake中使用全局定义预编译宏,来控制是否开启错误检查补充 分类 opengl c 引言 OpenGL希望在每次顶点着色器运行后,我们可见的所有顶点都为标准化设备坐标(Normalized Device Coordinate, NDC)。也就是说ÿ…...
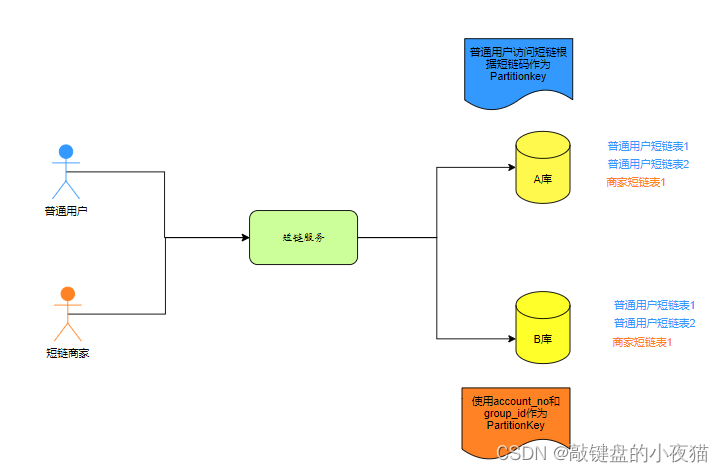
分库分表场景下多维查询解决方案(用户+商户)
在采用分库分表设计时,通过一个PartitionKey根据散列策略将数据分散到不同的库表中,从而有效降低海量数据下C端访问数据库的压力。这种方式可以缓解单一数据库的压力,提升了吞吐量,但同时也带来了新的问题。对于B端商户而言&#…...

vue学习日记14:工程化开发脚手架Vue CLI
一、概念 二、安装 1.全局安装&查看版本 注意启动cmd输入命令 要以管理员运行哦 安装了一次就行以后不用再创建了 yarn global addvue/cli vue --version 显示了版本号即可 2.创建项目架子 创建项目的路径在哪 项目就在哪 项目名字不能用中文 vue create project-n…...
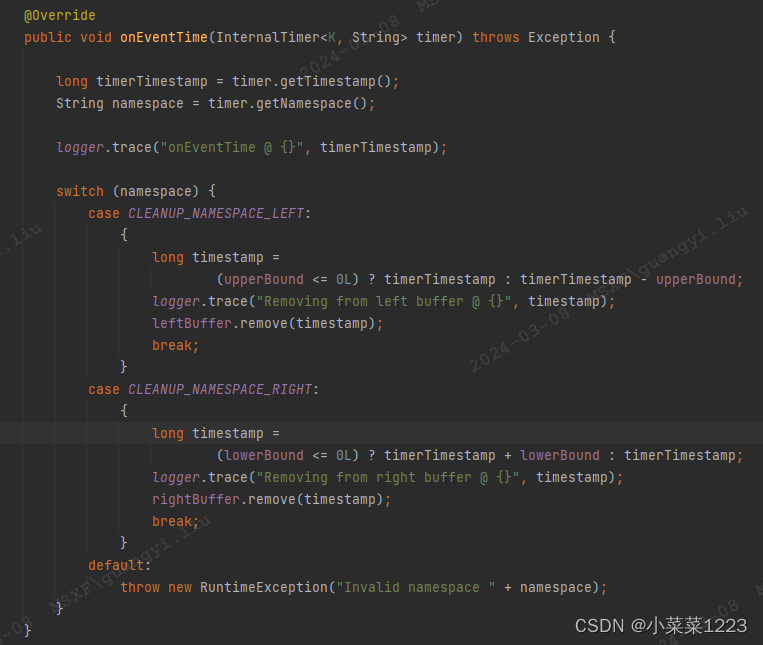
java Flink(四十三)Flink Interval Join源码解析以及简单实例
背景 之前我们在一片文章里简单介绍过Flink的多流合并算子 java Flink(三十六)Flink多流合并算子UNION、CONNECT、CoGroup、Join 今天我们通过Flink 1.14的源码对Flink的Interval Join进行深入的理解。 Interval Join不是两个窗口做关联,…...
JsonUtility.ToJson 和UnityWebRequest 踩过的坑记录
项目场景: 需求:我在做网络接口链接,使用的unity自带的 UnityWebRequest ,数据传输使用的json,json和自定义数据转化使用的也是unity自带的JsonUtility。使用过程中发现两个bug。 1.安全验证失败。 报错为:…...

面试算法-69-三角形最小路径和
题目 给定一个三角形 triangle ,找出自顶向下的最小路径和。 每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那…...
流畅的 Python 第二版(GPT 重译)(九)
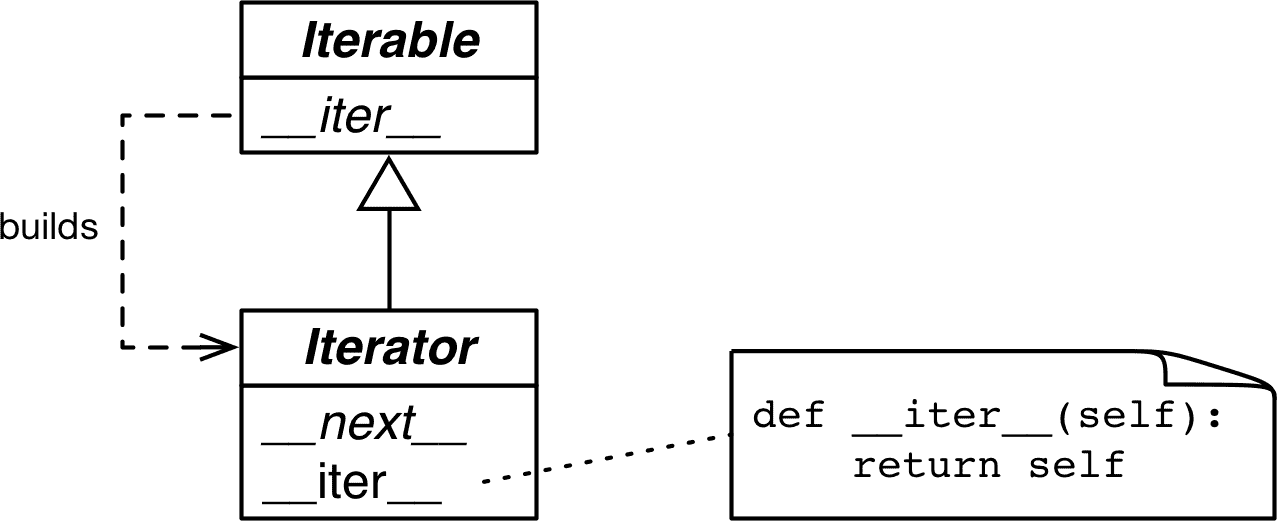
第四部分:控制流 第十七章:迭代器、生成器和经典协程 当我在我的程序中看到模式时,我认为这是一个麻烦的迹象。程序的形状应该只反映它需要解决的问题。代码中的任何其他规律性对我来说都是一个迹象,至少对我来说,这表…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...
