面试算法-69-三角形最小路径和
题目
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
示例 1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出:11
解释:如下面简图所示:
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
解
class Solution {public int minimumTotal(List<List<Integer>> triangle) {int n = triangle.size();int[][] dp = new int[n][n];dp[0][0] = triangle.get(0).get(0);for (int i = 1; i < n; i++) {for (int j = 0; j <= i; j++) {if (j == 0) {dp[i][0] = dp[i - 1][0] + triangle.get(i).get(0);} else if (i == j) {dp[i][j] = dp[i - 1][j - 1] + triangle.get(i).get(j);} else {dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j]) + triangle.get(i).get(j);}}}int min = Integer.MAX_VALUE;for (int i = 0; i < n; i++) {min = Math.min(min, dp[n - 1][i]);}return min;}
}
相关文章:

面试算法-69-三角形最小路径和
题目 给定一个三角形 triangle ,找出自顶向下的最小路径和。 每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那…...
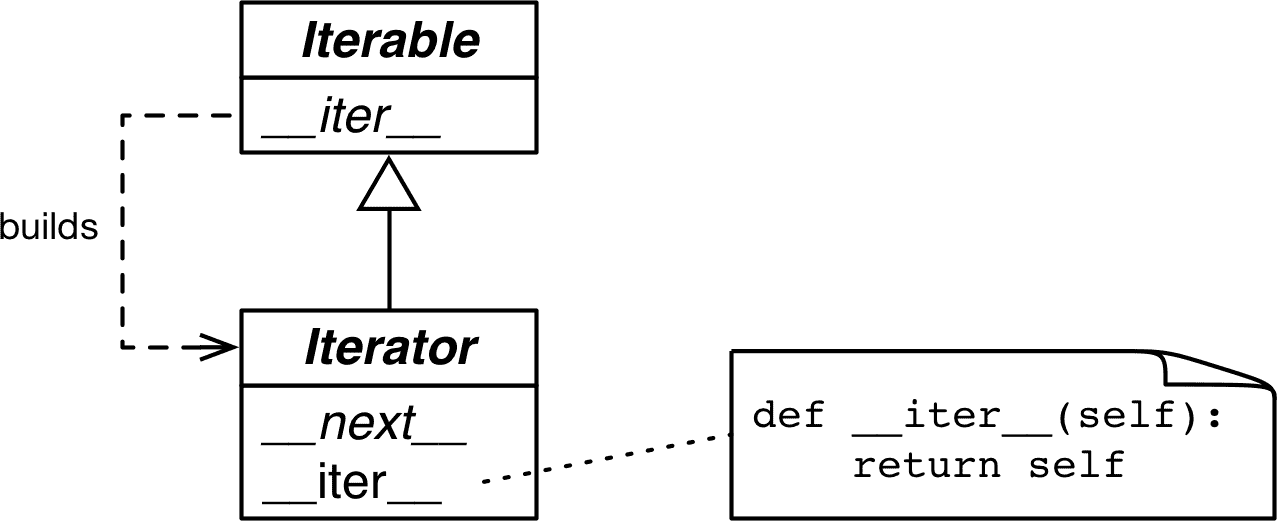
流畅的 Python 第二版(GPT 重译)(九)
第四部分:控制流 第十七章:迭代器、生成器和经典协程 当我在我的程序中看到模式时,我认为这是一个麻烦的迹象。程序的形状应该只反映它需要解决的问题。代码中的任何其他规律性对我来说都是一个迹象,至少对我来说,这表…...

单片机学到什么程度才可以去工作?
单片机学到什么程度才可以去工作? 如果没有名校或学位的加持,你还得再努力一把,才能从激烈的竞争中胜出。以下这些技能可以给你加分,你看情况学,不同行业对这些组件会有取舍: . Cortex-M内核:理解MCU内核各部件的工作机制&#…...

内网穿透方案
内网穿透 有几种流行的内网穿透软件可供选择,它们都能帮助你在内网环境中建立与外部网络的连接。以下是其中一些常用的内网穿透软件: Ngrok:Ngrok 是一个简单易用的内网穿透工具,可以快速创建安全的公共 URL,让你可以…...

WordPress菜单函数wp_nav_menu各参数
wordpress主题制作时,常常会在不同的位置调用不同的菜单,使用下面的这个代码,再加上CSS给菜单做新的样式,可满足wordpress模板制作时对菜单调用的所有需求。 wp_nav_menu( array( theme_location > ,//导航别名 menu > , /…...
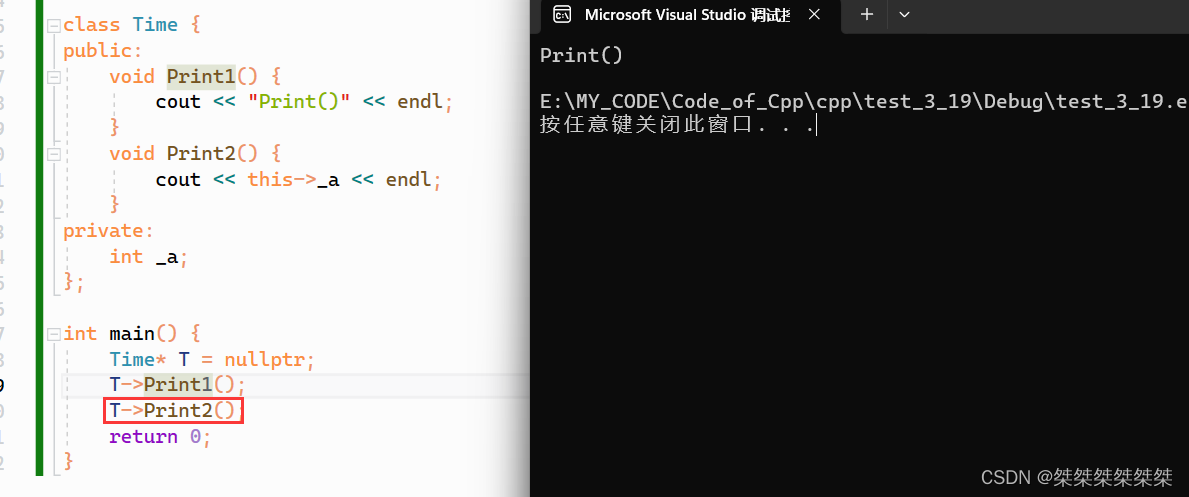
类于对象(上)--- 类的定义、访问限定符、计算类和对象的大小、this指针
在本篇中将会介绍一个很重要和很基础的Cpp知识——类和对象。对于类和对象的篇目将会有三篇,本篇是基础篇,将会介绍类的定义、类的访问限定符符和封装、计算类和对象的大小、以及类的 this 指针。目录如下: 目录 1. 关于类 1.1 类的定义 2 类…...
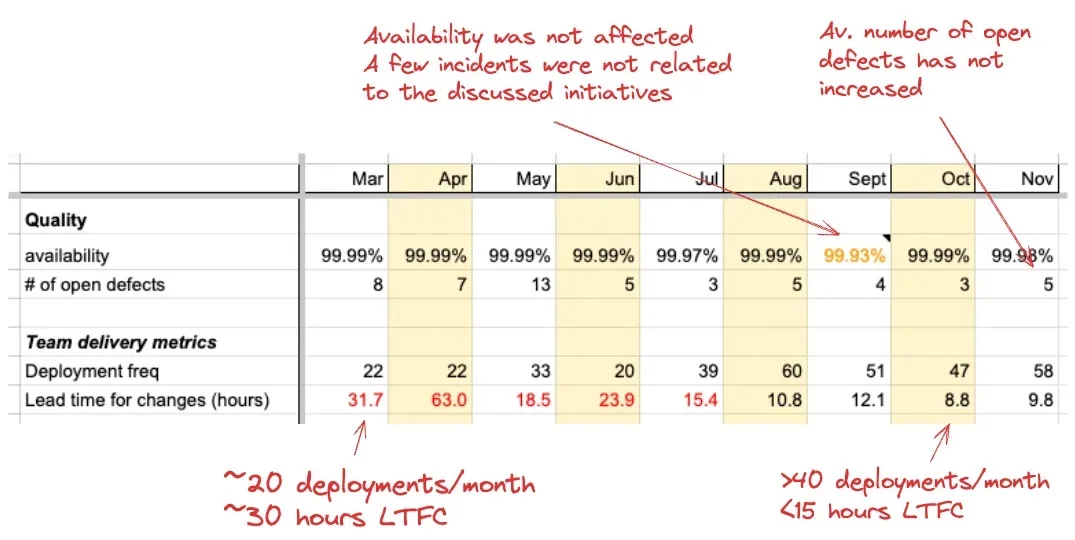
提升交付效率:Booking.com 金融技术团队的成功实践
Booking.com 金融技术业务部门的团队对其平台的后端和前端实施了一系列改进措施,并通过 DORA 指标将交付性能提高了一倍。此外,还使用了微前端 (MFE) 模式,将单体 FE 应用程序分解为多个可单独部署的分解应用程序。 2022 年年中,B…...

【消息队列开发】 实现ConsumerManager类——消费消息的核心逻辑
文章目录 🍃前言🌴扫描线程的实现🌲实现消费消息🌳实现addConsumer()方法🎋VirtualHost类订阅消息的完善⭕总结 🍃前言 本次开发目标 实现消费消息的核心逻辑 🌴扫描线程的实现 我们先给Cons…...

【Three.js】使用精灵图Sprite创建面朝相机的文本标注
目录 🐝前言 🐝canvas创建文字 🐝将canvas作为纹理贴图加载到sprite中 🐝封装方法 🐝前言 在Three.js中精灵Sprite是一个总是面朝摄像机的平面,它通常和纹理贴图结合使用,贴图可以是一张图…...

C++中的类模板
C中的类模板 类模板 类模板在C中是一种非常强大的工具,它允许程序员编写与数据类型无关的代码。简单来说,类模板允许你定义一个蓝图,这个蓝图可以用来生成具体类型的类。使用类模板可以提高代码的复用性,减少重复代码࿰…...

【每日一题】好子数组的最大分数
Tag 【单调栈】【暴力枚举】【数组】【2024-03-19】 题目来源 1793. 好子数组的最大分数 解题思路 本题和 84. 柱状图中最大的矩形 一样,计算的都是最大矩形的面积。只不过多了一个约束:矩形必须包含下标 k。 以下的方法一和方法二是 84. 柱状图中最…...
Vue2(七):超详细vue开发环境搭建(win7),nodejs下载与安装,安装淘宝镜像(报错已解决),配置脚手架
一、安装node.js 本来想粗略写一下的,但是搭建脚手架的时候,遇到了很多问题,浪费快两天时间,记录一下自己的解决办法希望对你们有帮助! 1.下载nodejs 安装包下载链接【CNPM Binaries Mirror】 下载我划线的这个&am…...
【Web】记录CISCN 2021 总决赛 ezj4va题目复现——AspectJWeaver
目录 前言 原理分析 step 0 step 1 EXP 前文:【Web】浅聊Java反序列化之AspectJWeaver——任意文件写入-CSDN博客 前言 这就是当年传说中的零解题嘛😭,快做🤮了 有了之前的经验,思路顺挺快的,中间不…...
视频技术1:使用ABLMediaServer推流rtsp
ABLMediaServer定位是高性能、高稳定、开箱即用、商用级别的流媒体服务器 下边展示了如何把1个mp3作为输入源,转换为rtsp流的过程。 作用:用rtsp模拟摄像头的视频流 1、启动ABLMediaServer ABLMediaServer-2024-03-13\WinX64\ABLMediaServer.exe 配…...

HTML5+CSS3+JS小实例:创意罗盘时钟
实例:创意罗盘时钟 技术栈:HTML+CSS+JS 效果: 源码: 【HTML】 <!DOCTYPE html> <html lang="zh-CN"><head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=…...

设计数据库之内部模式:SQL基本操作
Chapter4:设计数据库之内部模式:SQL基本操作 笔记来源: 1.《漫画数据库》—科学出版社 2.SQL | DDL, DQL, DML, DCL and TCL Commands 设计数据库的步骤: 概念模式 概念模式(conceptual schema)是指将现实世界模型化的阶段进而&…...
Git浅谈配置文件和免密登录
一、文章内容 简述git三种配置ssh免密登录以及遇见的问题git可忽略文件git remote 相关操作 二、Git三种配置 项目配置文件(局部):项目路径/.git/config 文件 git config --local user.name name git config --local user.email 123qq.cc全局配置文(所有用户): …...

【好玩的经典游戏】Docker环境下部署RPG网页小游戏
【好玩的经典游戏】Docker环境下部署RPG网页小游戏 一、react-tetris小游戏介绍1.1 react-tetris小游戏简介1.2 项目预览二、本次实践介绍2.1 本地环境规划2.2 本次实践介绍三、本地环境检查3.1 安装Docker环境3.2 检查Docker服务状态3.3 检查Docker版本3.4 检查docker compose…...

前端逻辑错误或UI崩溃解决问题
全屏错误覆盖层或UI崩溃 VueReact(错误边界) Vue Vue的全屏错误覆盖层解决,其实只需要配置Error就好,在开发服务器的client.overlay中设置关闭全屏覆盖层 module.exports {devServer: {client: {overlay: {warnings: false,error…...
python爬取QQ音乐评论信息
python爬取QQ音乐评论信息 python爬取QQ音乐评论信息1.随便选个音乐python爬取QQ音乐评论信息 1.随便选个音乐 https://y.qq.com/n/yqq/song/0039MnYb0qxYhV.html 当前的后台调试页面显示如下: 找到评论的数据接口: https://c.y.qq.com/base/fcgi-bin/fcg_global_comme…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
