2016年认证杯SPSSPRO杯数学建模B题(第二阶段)多帧图像的复原与融合全过程文档及程序
2016年认证杯SPSSPRO杯数学建模
B题 多帧图像的复原与融合
原题再现:
数码摄像技术被广泛使用于多种场合中。有时由于客观条件的限制,拍摄设备只能在较低的分辨率下成像。为简单起见,我们只考虑单色成像。假设成像的分辨率为 32 × 64,成像方式是将整个矩形视野划分成 32 × 64 个相同大小的矩形格子,图像中每个像素的取值为对应格子的亮度平均值。每间隔一定时间拍摄一帧图像,运动的画面体现为图像的序列。
第二阶段问题: 对一副静态的图像而言,每个像素对应于视野中的一个格子,每个格子内部的细节信息已经无法还原。但如果在视野移动的过程中拍摄系列图像,我们通过对多帧图像进行对比分析,仍然有可能还原出来一些在单张照片中无法体现的细节。请建立合理的数学模型和算法,通过对多帧图像进行分析,尽可能多地还原出被摄物的细节。
整体求解过程概述(摘要)
随着计算机技术的发展,人们对于图像美观的需求越来越高,图像处理技术也逐渐成为了一个热点问题。然而,人们所得到的图像并不一定是清晰而且完整的。在对图像的进行收集时,有众多的因素会引起所收集图像的分辨率的下降和图像失真,其主要表现为模糊、噪声和丢失像素点。造成模糊的因素有很多,例如由被拍摄的运动对象所带来的运动模糊现象、拍摄仪器的大光圈所带来的散焦现象以及当矢量图转化为位图时所导致的失真现象等。为了解决以上问题,我们对多种算法进行了分析比较:
对于低分辨率下运动图片中的细节缺失问题,我们使用了基于维纳滤波器的几何均值滤波算法作为基础的复原模型。我们对多张合适的单色、模糊图片进行统计分析并优化得到合适的算法。通过实验我们发现:要保证模型所匹配到缺失细节的数量和准确度,需要重点考虑两点因素:相邻两幅运动图像的相似程度和特征块匹配及其融合。对于前者,我们使用了交叉熵和峰值信噪比作为评判指标;对于后者,我们在不同情况分别使用了傅里叶变换、小波变换的方式择优进行融合。
在模型的对比验证阶段,我们分别利用了传统滤波算法和本文提出的多帧图像复原与融合模型进行图像复原,并通过实验体现了我们提出模型的效率;最后,我们使用峰值信噪比、信息熵、均方差等数据进行实验结果分析并验证了模型的健壮性。
问题分析:
题目要求研究单色成像,那么每一个像素点的区别就是用格子的亮度来表示。对于一个32×64 的矩阵格子,我们可以生成一个大小为32×64 的亮度矩阵来模拟视野中观察到的图像。随着物体在视野区域向某个方向移动,亮度矩阵会随之有规律的变化。
题目没有明确规定间隔多少时间拍摄一帧图像。由于视野向某个方向缓慢运动,不同的时间间隔拍摄图像,在同一帧中视野区域内容也不一样。将拍摄时间间隔作为变量,建立的算法要求在足够大的拍摄时间间隔下实现较高的识别度。
题目要求通过多帧图像对比分析还原出在单张照片中无法体现的细节。在建立模型的过程中,我们仍需考虑现有的单张图片还原算法处理模糊图片,再将本文的算法模型进行对比,体现出多帧图像处理的优势。题目要求尽可能多的还原出被摄物的细节。即在不限定算法时间复杂度的前提下(电脑能够运行完成算法即可),还原出被摄物最多的细节。
被摄物的细节可以由主观评价和客观评价组成。主观评价可以由多准则决策方法实现。但由于该题需要客观地评价被摄物的细节,我们的模型通过大量客观的图像评价指标评价算法细节还原效率以及准确度,主观评价部分展示经过算法处理的图片,文中不作主观评价。
模型假设:
1. 假设计算机能接受的亮度的范围为0至255。那么亮度矩阵表示为由0至255构成,大小为32×64 的亮度矩阵。
2. 假设原始的图像噪声足够少,使得肉眼能够分辨出图片的部分细节。
3. 假设拍摄的时间间隔足够小,使相邻两组视野中图像有相同的特征便于算法提取。
4. 假设相机在运动过程拍摄的照片会产生模糊,从而导致照片细节不清晰。
5. 假设选取的进行实验的20张随机图片样本可以代表总体。
6. 假设算法运行的实验环境相同。
论文缩略图:


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
1 clc
2 clear all
3 close all
4 %for i=1:2
5 I=imread(’7.png’);
6 %subplot(231);
7 figure(1)
8 imshow(I);
9 I=rgb2gray(I);
10 %subplot(232);
11 figure(2)
12 imshow(I);
13 noise=0.1*randn(size(I));
14 PSF=fspecial(’motion’,21,11);
15 Blurred=imfilter(I,PSF,’circular’);
16 BlurredNoisy=im2uint8(Blurred);
17 NP=abs(fftn(noise)).ˆ2;
18 NPOW=sum(NP(:)/prod(size(noise)));
19 NCORR=fftshift(real(ifftn(NP)));
20 IP=abs(fftn(I)).ˆ2;
21 IPOW=sum(IP(:)/prod(size(noise)));
22 ICORR=fftshift(real(ifftn(IP)));
23 ICORR1=ICORR(:,ceil(size(I,1)/2));
24 NSR=NPOW/IPOW;
25 %subplot(233);
26 figure(3)
27 imshow(BlurredNoisy,[]);
28 %title(’第一帧’);
29 %subplot(234);
30 figure(4)
31 imshow(deconvwnr(BlurredNoisy,PSF),[]);
32 %title(’deconbwnr(A,PSF,NSR)’);
33 %subplot(235);
34 figure(5)
35 imshow(deconvwnr(BlurredNoisy,PSF,NCORR,ICORR),[]);
36 %title(’deconbwnr(A,PSF,NCORR,ICORR)’);
37 %subplot(236);
38 figure(6)
39 pic=imshow(deconvwnr(BlurredNoisy,PSF,NPOW,ICORR1),[]);
40 %title(’deconbwnr(A,PSF,NPOW,ICORR_1_D)’);
41 %end
1 load wbarb; X1 = X; map1 = map; subplot( 2,2,1) ;
2 image( X1) ; colormap( map1) ; title( ’图像wbarb’) ;
3 load woman; X2 = X; map2 = map; subplot( 2,2,2) ;
4 image( X2) ; colormap( map2) ; title( ’图像woman’) ;
5 [C1,L1]= wavedec2( X1,2,’sym4’) ; [C2,L2]=wavedec2( X2,2,’sym4’) ; C = C1
+ C2;
6 XX = waverec2( C,L1,’sym4’) ; subplot( 2,2,3) ; image( XX) ; colormap(map1) ; title( ’小波融
合1’) ;
7 Csize1 = size( C1) ;
8 for i = 1: Csize1( 2)
9 C1( i) = 1.2*C1( i) ;
10 end
11 Csize2 = size( C2) ;
12 for j = 1: Csize2( 2)
13 C2( j) = 0.8* C2( j) ;
14 end
15 C = 0.5* ( C1 + C2) ; XXX = waverec2( C,L2,’sym4’) ;
16 subplot( 2,2,4) ; image( XXX) ; colormap( map2) ; title( ’小波融合2’);
全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2016年认证杯SPSSPRO杯数学建模B题(第二阶段)多帧图像的复原与融合全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 B题 多帧图像的复原与融合 原题再现: 数码摄像技术被广泛使用于多种场合中。有时由于客观条件的限制,拍摄设备只能在较低的分辨率下成像。为简单起见,我们只考虑单色成像。假设成像的分辨率为 32 64&#x…...
WMI接口设计实现
WMI是Windows操作系统管理数据和操作的基础设施,系统管理员可以使用VB Script、PowerShell及Windows API(C、C#等)管理本地或远程计算机。 使用WMI框架应用程序可以直接访问EC RAM、 I/O端口、Memory地址、寄存器、Setup NV设定值,…...
前端项目,个人笔记(二)【Vue-cli - 引入阿里矢量库图标 + 吸顶交互 + setup语法糖】
目录 1、项目中引入阿里矢量库图标 2、实现吸顶交互 3、语法糖--<script setup> 3.1、无需return 3.2、子组件接收父组件的值-props的使用 3.3、注册组件 1、项目中引入阿里矢量库图标 步骤一:进入阿里矢量库官网中:iconfont-阿里巴巴矢量…...

OpenCV 介绍使用
返回:OpenCV系列文章目录(持续更新中......) 上一篇:OpenCV4.9.0开源计算机视觉库使用简要说明 下一篇: OpenCV(开源计算机视觉库:http://opencv.org)是一个开源库,包含数百种计算机视觉算法。…...

Python 10个面试题实例
当然!以下是10个Python面试题及其示例解决方案的中题目: 1.反转字符串: string "Hello, World!" reversed_string string[::-1] print(reversed_string)2.检查字符串是否为回文: def is_palindrome(string):return string string[::-1]r…...
Python:熟悉简单的skfuzzy构建接近生活事件的模糊控制器”(附带详细注释说明)+ 测试结果
参考资料:https: // blog.csdn.net / shelgi / article / details / 126908418 ————通过下面这个例子,终于能理解一点模糊理论的应用了,感谢原作。 熟悉简单的skfuzzy构建接近生活事件的模糊控制器 假设下面这样的场景, 我们希望构建一套…...

opencv函数使用查找
opencv官方文档地址:https://docs.opencv.org/4.x/index.html 先选对应的版本opencv-python 以这个函数为例子 model cv2.face.LBPHFaceRecognizer.create() 点开后找face类的LBP里面就有create函数的用法...

使用 pypdf 快速切分 PDF 文件
categories: [Python] tags: Python MacOS 写在前面 最近有小伙伴问我怎么把 PDF 文档切分成两个大小相近的 PDF文档, 要是在 mac 上, 直接无脑预览就行了, 但是这样不够跨平台, 之后我也尝试过 pymupdf, 但是奈何不支持 arm 架构, 后来还是用 Python 原生的 pypdf 了. 有 AI…...

Avalonia(11.0.2)+.NET6 打包运行到银河麒麟V10桌面系统
操作系统配置 项目结构 .net版本 这次我们是在银河麒麟V10系统上打包运行Avalonia(11.0.2)+.NET6.0的程序 开始打包 准备Linux下的桌面快捷方式以及图标 调整AvaloniaApplication2.Desktop.csproj的配置项,重点看下图红色线圈出来的部分,里面涉及到了LinuxPath的设置。完整的配…...
Mac nvm install failed python: not found
报错 $>./configure --prefix/Users/xxx/.nvm/versions/node/v12.22.12 < ./configure: line 3: exec: python: not found nvm: install v12.22.12 failed!解决方法 到 App 文件夹,并且打开 cd /System/Applications/Utilities/ open .记得改完 Rosetta 之…...

C语言基础知识复习(考研)
(1)C语言文件操作 1 什么是文件 文件有不同的类型,在程序设计中,主要用到两种文件: (1)程序文件。包括源程序文件(后缀为.c)、目标文件(后缀为.obj)、可执行这种文件的内容是程序代码。 (2)数据文件。文件的内容不是…...

Prometheus Grafana 配置仪表板
#grafana# 其实grafana提供了丰富的Prometheus数据源的仪表板,基本上主流的都有,通过下面官方地址可查阅 Dashboards | Grafana Labs 这里举例说明,配置node_exporter仪表板 首先,在上面的网站搜索 node 可以查到蛮多的仪表板…...
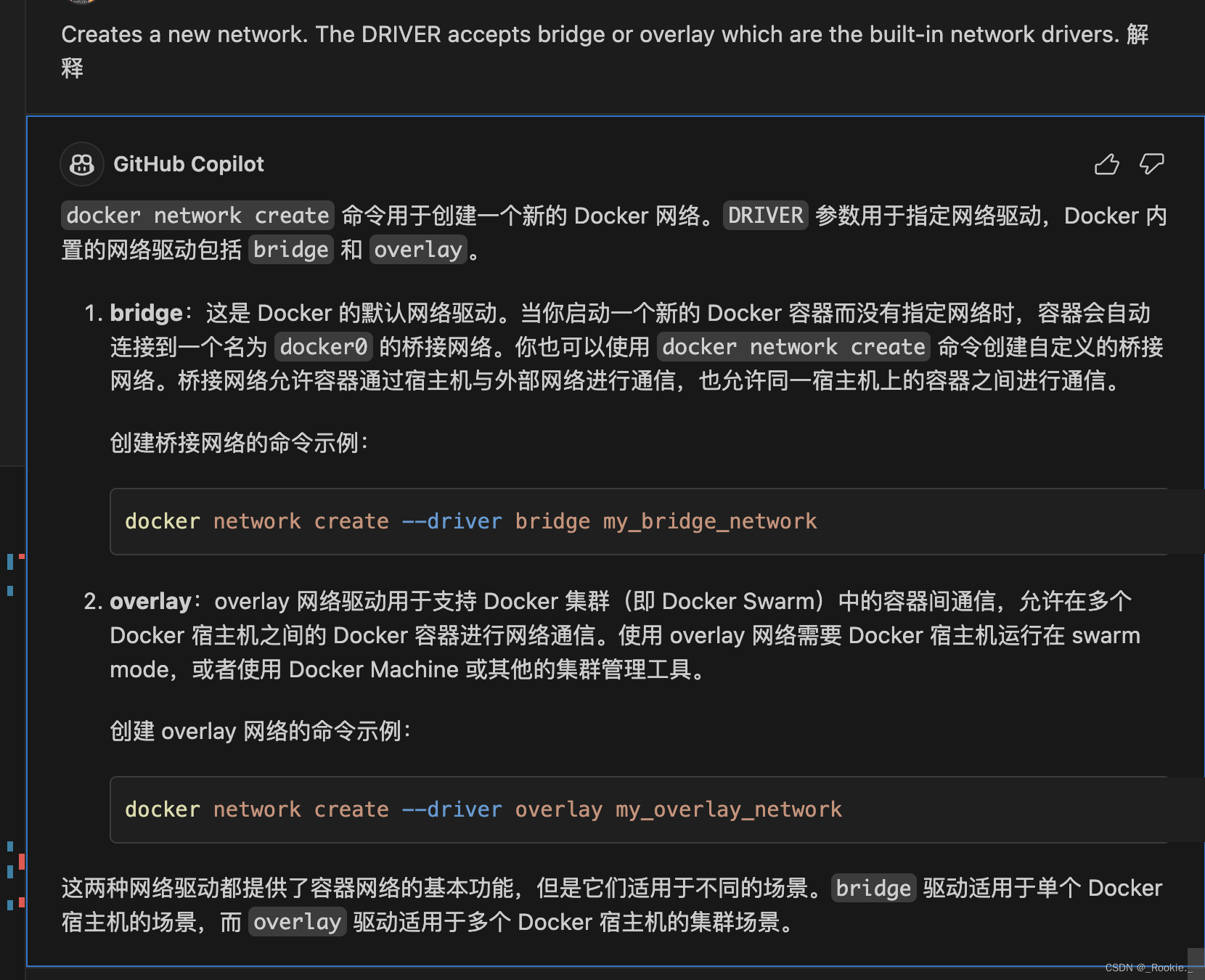
docker 哲学 - 网络桥接器、容器网络接口 、容器间的通信方式
1、解释 docker0 veth eth 2、vethXX 和 ethXX 是肯定一一对应吗 比如 eth1 对应 veth1 3、如果 A容器使用 默认创建方式 。定义他内部网络为 eth0,容器B使用 --network 连上 已创建的网络 172.89.2.1 。此时假设 B的 ip是 172.89.2.2 ,容器网络接口是 e…...
Python 将HTML转为PDF、图片、XML、XPS格式
网页内容是信息传播的主要形式之一。在Web开发中,有时候我们需要将HTML文件以不同的格式保存或分享,比如PDF、图片(如PNG或JPEG)、XML或XPS等。这些格式各有优势,适合不同的用途。在这篇文章中,我们将介绍如…...
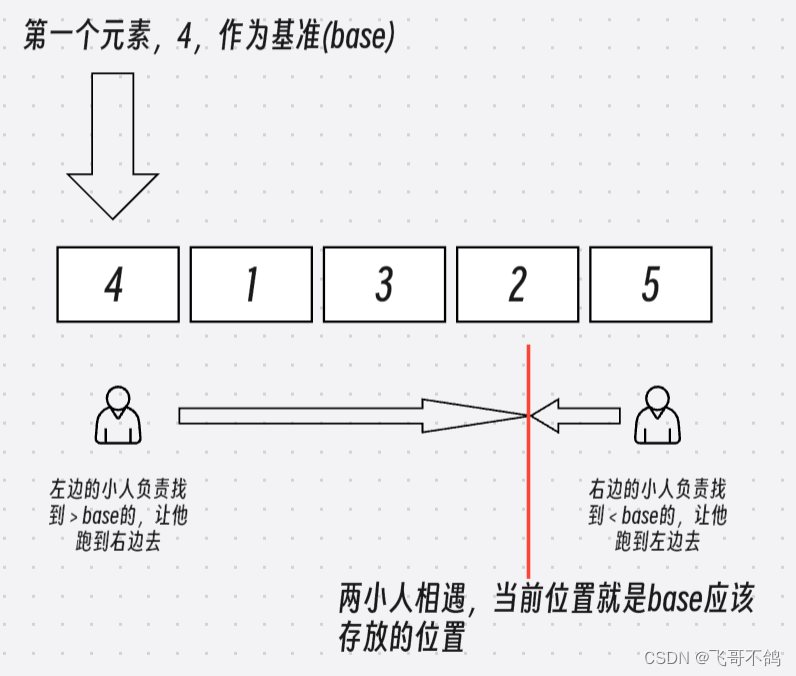
排序算法记录(冒泡+快排+归并)
文章目录 前言冒泡排序快速排序归并排序 前言 冒泡 快排 归并,这三种排序算法太过经典,但又很容易忘了。虽然一开始接触雀氏这些算法雀氏有些头大,但时间长了也还好。主要是回忆这些算法干了啥很耗时间。 如果在笔试时要写一个o(nlogn)的…...

简单聊聊如何更优雅地初始化对象:构造函数、Builder模式和静态工厂方法比较
大家好,我是G探险者。 在平时的java编程中,你肯定会有过对一些实体对象进行初始化的set操作,有的对象的属性较少可能还好点,当一个对象拥有许多属性时,通常的初始化方式可能显得笨拙而不直观,代码写的很不…...

跳过mysql权限验证来修改密码-GPT纯享版
建议重新配置一遍,弄成功好多次了,每次都出bug,又要重新弄,不是过期就是又登不进去了,我服了 电脑配置MySQL环境(详细)这个哥们的10min配完,轻轻松松, 旧方法ÿ…...

Vue3快速上手(十七)Vue3之状态管理Pinia
一、简介 Pinia官网:https://pinia.vuejs.org/zh/ 从官网截图里可以直接看到,pinia是一个vuejs的状态(数据)管理工具。功能性同vuex。logo是小菠萝。它是一个集中式状态管理工具。就是将多个组件共用的数据管理起来,重复利用。有点类似缓存的意思。 二、Pinia环境搭建 …...
时序预测 | Matlab实现BiTCN-GRU双向时间卷积神经网络结合门控循环单元时间序列预测
时序预测 | Matlab实现BiTCN-GRU双向时间卷积神经网络结合门控循环单元时间序列预测 目录 时序预测 | Matlab实现BiTCN-GRU双向时间卷积神经网络结合门控循环单元时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.Matlab实现BiTCN-GRU双向时间卷积神经网络结…...

学习笔记Day14:Linux下软件安装
软件安装 Anaconda 所有语言的包(package)、依赖(dependency)和环境(environment)管理器,类似应用商店 Conda < Miniconda < Anaconda(有交互界面) Linux下Miniconda即可 安装Miniconda 搜索北外/清华miniconda镜像网站ÿ…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
