【React 】React 性能优化的手段有哪些?
1. 是什么
React凭借virtual DOM和diff算法拥有高效的性能,但是某些情况下,性能明显可以进一步提高
在前面文章中,我们了解到类组件通过调用setState方法,就会导致render ,父组件一旦发生render渲染,子组件一定也会执行render渲染
2. 如何做
在React中如何避免不必要的render中,我们了解到如何避免不必要的render来应付上面的问题,主要手段是通过shouldComponentUpdate、PureComponent 、React.memo ,这三种形式这里就不再复述
除此之外,常见性能优化常见的手段有如下:
- 避免使用内联函数
- 使用React Fragments避免额外标记
- 使用Immutable
- 懒加载组件
- 事件绑定方式
- 服务端渲染
2.1 避免使用内联函数
如果我们使用内联函数,则每次调用render函数时都会创建一个新的函数实例,如下:
import React from "react";
export default class InlineFunctionComponent extends React.Component {render() {return ( <div> <h1>Welcome RUI </h1> <input type="button" onClick={(e) => { this.setState({inputValue: e.target.value}) }} value="Click For Inline Function" /></div> ) }
}
我们应该在组件内部创建一个函数,并将事件绑定到该函数本身。这样每次调用render时就不会创建单独的函数实例,如下:
import React from "react";
export default class InlineFunctionComponent extends React.Component {setNewStateData = (event) => {this.setState({inputValue: e.target.value}) }render() {return ( <div> <h1>Welcome Guest</h1> <input type="button" onClick={this.setNewStateData} value="Click For Inline Function" /></div> ) }
}
2.2 使用React Fragments避免额外标记
用户创建新组件时,每个组件应具有单个父标签。父级不能有两个标签,所以顶部要有一个公共标签,所以我们经常在组件顶部添加额外标签div
这个额外标签除了充当父标签之外,并没有其他作用,这时候则可以使用fragement <> 其不会向组件引入任何额外标记,但它可以作为父级标签的作用
2.3 事件绑定方式
在事件绑定方式中,我们了解到四种事假绑定的方式
从性能方面考虑,在render方法中使用bind和render方法中使用箭头函数这两种形式在每次组件render的时候都会生成新的方法实例,性能欠缺
而constructor中bind事件与定义阶段使用箭头函数绑定这两种形式只会生成一个方法实例,性能方面会有所改善
2.4 使用Immutable
我们了解到使用Immutable可以给React应用带来性能的优化,主要体现在减少渲染的次数在做react性能优化的时候,为了避免重复渲染,我们会在shouldComponentUpdate()中做对比,当返回true执行render方法Immutable通过is方法则可以完成对比,而无需像一样通过深度比较的方式比较
2.5 懒加载组件
从工程方面考虑,webpack存在代码拆分能力,可以为应用创建多个包,并在运行时动态加载,减少初始包的大小
而在react中使用到了Suspense和lazy组件实现代码拆分功能,基本使用如下:
const johanComponent = React.lazy(() => import(/* webpackChunkName: "johanC
omponent" */ './myAwesome.component'));
export const johanAsyncComponent = props => ( <React.Suspense fallback={<Spinner />}> <johanComponent {...props} /></React.Suspense>
);
2.6 服务端渲染
采用服务端渲染端方式,可以使用户更快的看到渲染完成的页面
服务端渲染,需要起一个node服务,可以使用express、koa等,调用react的renderToString方法,将根组件渲染成字符串,再输出到响应中
2.7 其他
除此之外,还存在的优化手段有组件拆分、合理使用hooks等性能优化手段…
3. 总结
通过上面初步学习,我们了解到react常见的性能优化可以分成三个层面:
- 代码层面
- 工程层面
- 框架机制层面
通过这三个层面的优化结合,能够使基于react项目的性能更上一层楼
相关文章:

【React 】React 性能优化的手段有哪些?
1. 是什么 React凭借virtual DOM和diff算法拥有高效的性能,但是某些情况下,性能明显可以进一步提高 在前面文章中,我们了解到类组件通过调用setState方法,就会导致render ,父组件一旦发生render渲染,子组件一定也会执…...
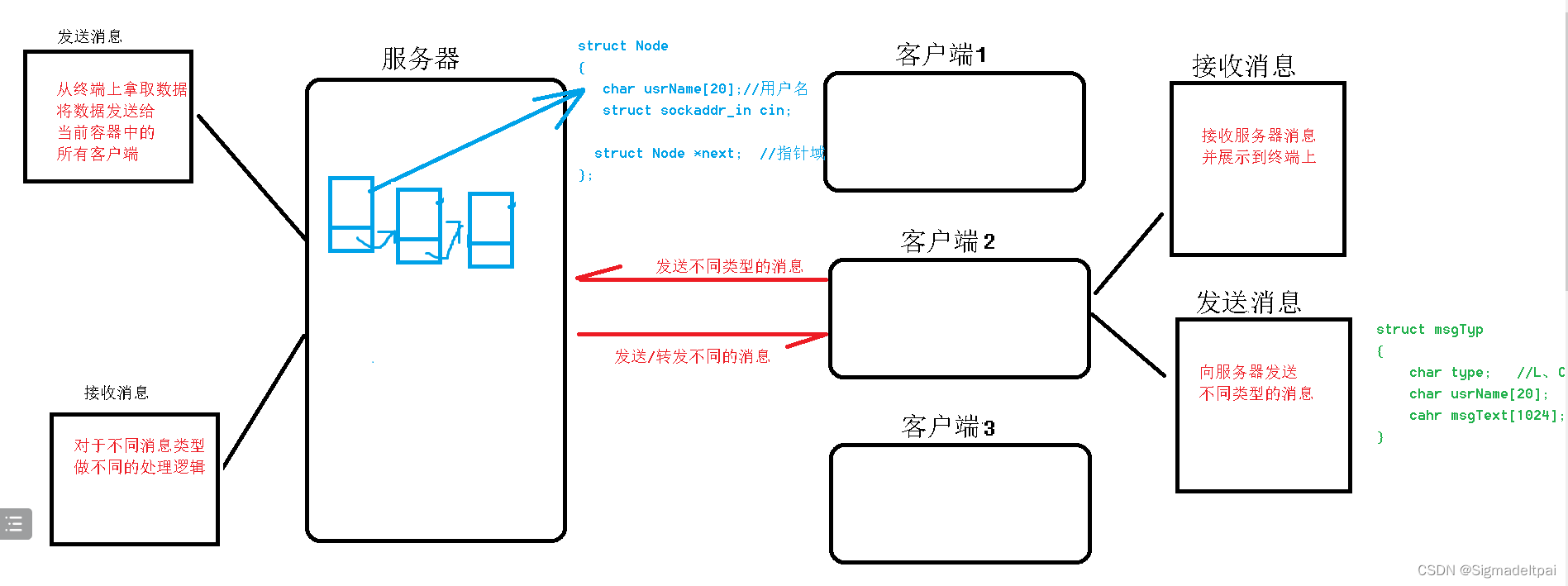
3.22网络编程小项目
基于UDP的网络聊天室 项目需求: 如果有用户登录,其他用户可以收到这个人的登录信息如果有人发送信息,其他用户可以收到这个人的群聊信息如果有人下线,其他用户可以收到这个人的下线信息服务器可以发送系统信息 服务器 #includ…...
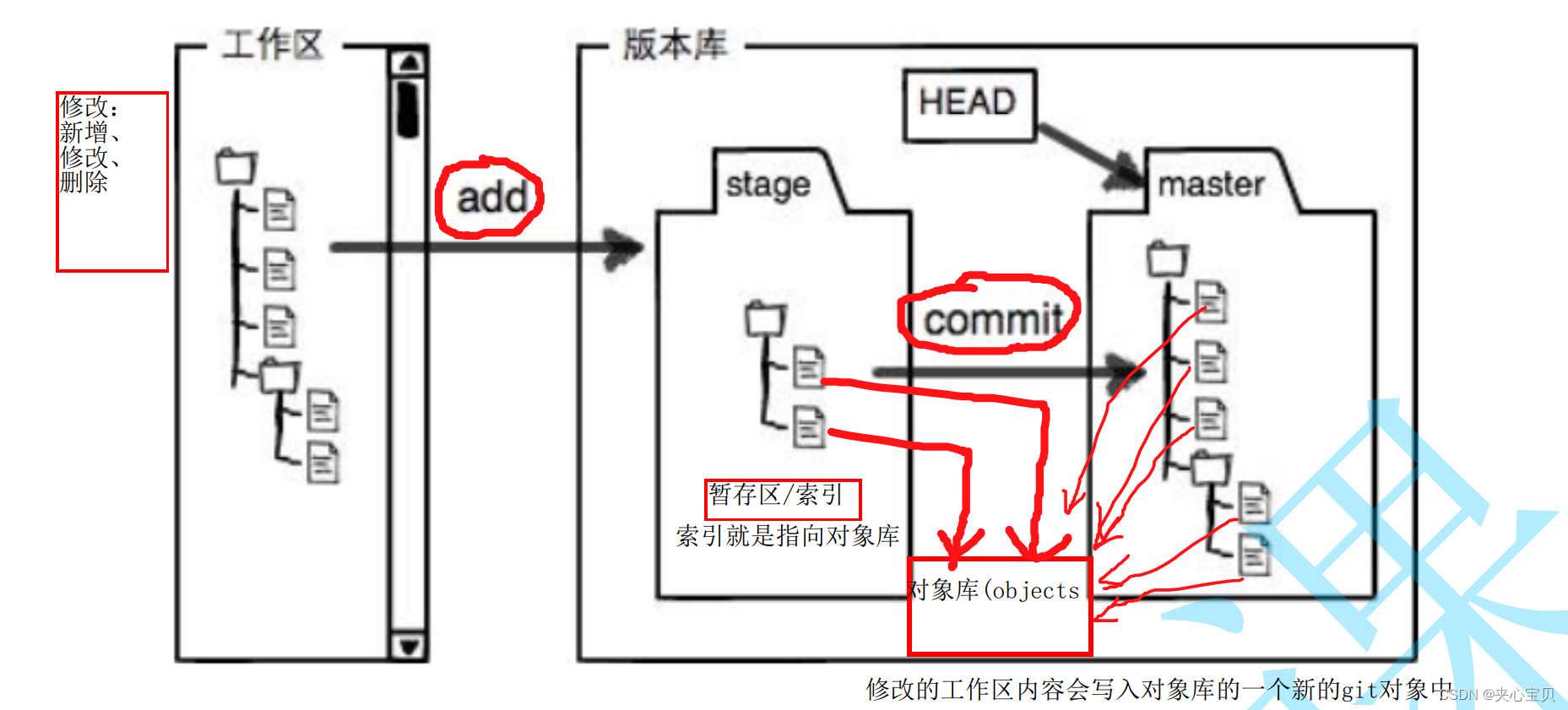
Git原理及使用
1、Git初识 Git是一种版本控制器: 对于同一份文件,做多次改动,Git会记录每一次改动前后的文件。 通俗的讲就是⼀个可以记录⼯程的每⼀次改动和版本迭代的⼀个管理系统,同时也⽅便多⼈协同作业。 注意: Git其实只能跟踪⽂本⽂件的改动,⽐如TXT⽂件,⽹⻚,所有的程序代码…...
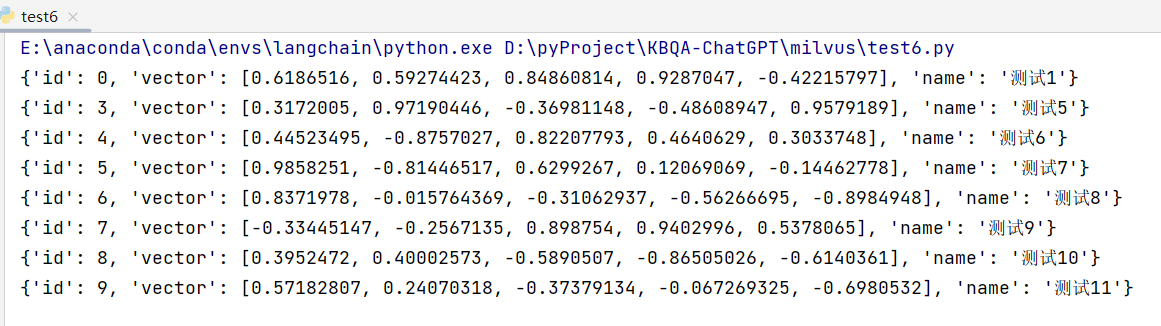
Milvus 向量数据库介绍及使用
一、Milvus 介绍及安装 Milvus 于 2019 年创建,其目标只有一个:存储、索引和管理由深度神经网络和其他机器学习 (ML) 模型生成的大量嵌入向量。它具备高可用、高性能、易拓展的特点,用于海量向量数据的实时召回。 作为专门为处理输入向量查…...
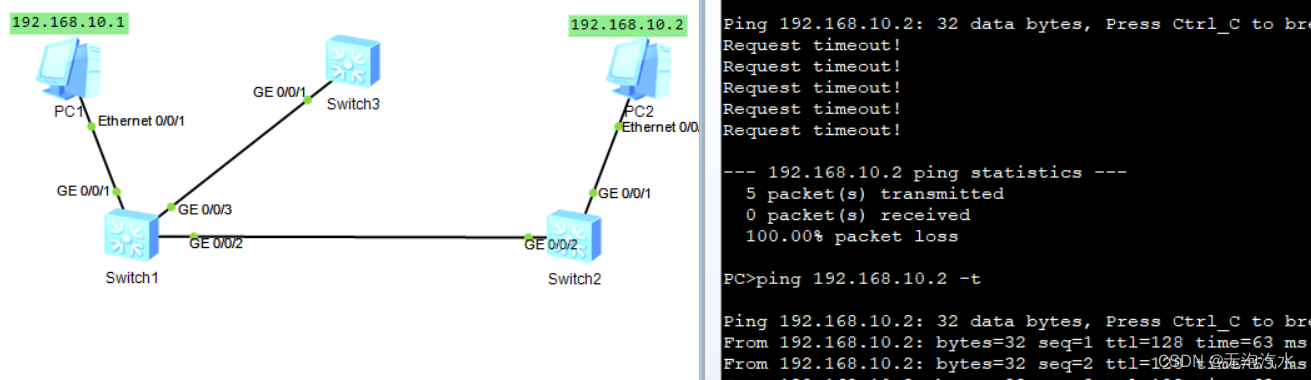
STP环路避免实验(华为)
思科设备参考:STP环路避免实验(思科) 一,技术简介 Spanning Tree Protocol(STP),即生成树协议,是一种数据链路层协议。主要作用是防止二层环路,并自适应网络变化和故障…...

二、SpringBoot3 配置文件
本章概要 统一配置管理概述属性配置文件使用YAML 配置文件使用批量配置文件注入多环境配置和使用 2.1 统一配置管理概述 SpringBoot工程下,进行统一的配置管理,你想设置的任何参数(端口号、项目根路径、数据库连接信息等等)都集中到一个固定…...
二、阅读器的开发(初始)-- 2、阅读器开发
1、epubjs核心工作原理 1.1 epubjs的核心工作原理解析 epub电子书,会通过epubjs去实例化一个Book对象,Book对象会对电子书进行解析。Book对象可以通过renderTo方法去生成一个Rendition对象,Rendition主要负责电子书的渲染,通过R…...
【QT入门】 Qt自定义信号后跨线程发送信号
往期回顾: 【QT入门】 lambda表达式(函数)详解-CSDN博客 【QT入门】 Qt槽函数五种常用写法介绍-CSDN博客 【QT入门】 Qt实现自定义信号-CSDN博客 【QT入门】 Qt自定义信号后跨线程发送信号 由于Qt的子线程是无法直接修改ui,需要发送信号到ui线程进行修改…...
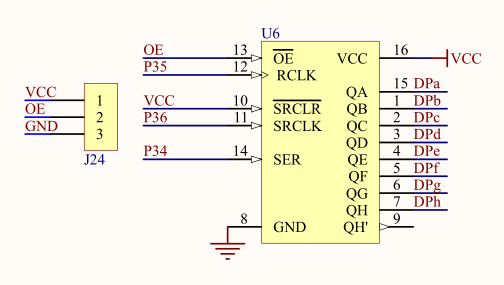
51单片机学习笔记7 串转并操作方法
51单片机学习笔记7 串转并操作方法 一、串转并操作简介二、74HC595介绍1. **功能**:2. **引脚**:3. **工作原理**:4. 开发板原理图(1)8*8 LED点阵:(2)74HC595 串转并: 三…...
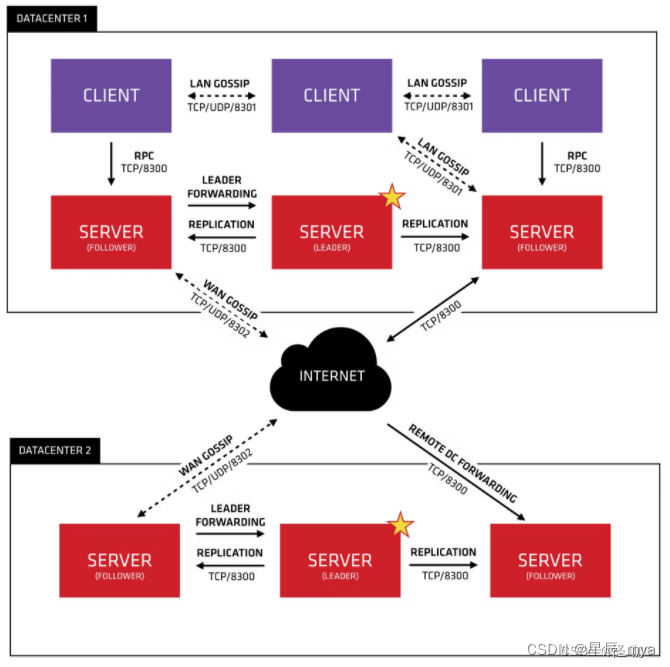
微服务cloud--抱团取暖吗 netflix很多停更了
抱团只会卷,卷卷也挺好的 DDD 高内聚 低耦合 服务间不要有业务交叉 通过接口调用 分解技术实现的复杂性,围绕业务概念构建领域模型;边界划分 业务中台: 数据中台: 技术中台: 核心组件 eureka&#x…...

牛客笔试|美团2024春招第一场【测试方向】
第一题:小美的数组询问 小美拿到了一个由正整数组成的数组,但其中有一些元素是未知的(用 0 来表示)。 现在小美想知道,如果那些未知的元素在区间 [l, r] 范围内随机取值的话,数组所有元素之和的最小值和最大…...
:前言)
Docker搭建LNMP环境实战(一):前言
缘起:不久前学习了Docker相关知识,并在Docker环境下学习了LNMP环境的搭建。由于网上的文章大多没有翔实、可行的案例,很多文章都是断章取义,所以,期间踩了太多太多的坑,初学者想要真正顺利地搭建一套环境起…...

SCI一区 | Matlab实现PSO-TCN-BiGRU-Attention粒子群算法优化时间卷积双向门控循环单元融合注意力机制多变量时间序列预测
SCI一区 | Matlab实现PSO-TCN-BiGRU-Attention粒子群算法优化时间卷积双向门控循环单元融合注意力机制多变量时间序列预测 目录 SCI一区 | Matlab实现PSO-TCN-BiGRU-Attention粒子群算法优化时间卷积双向门控循环单元融合注意力机制多变量时间序列预测预测效果基本介绍模型描述…...
界面控件DevExpress ASP.NET Ribbon组件 - 完美复刻Office 365体验!
无论用户是喜欢传统工具栏菜单外观、样式,还是想在下一个项目中复制Office 365 web UI,DevExpress ASP.NET都提供了所需要的工具,帮助用户打造更好的应用程序界面。 P.S:DevExpress ASP.NET Web Forms Controls拥有针对Web表单&a…...

vue2【详解】mixins —— 抽离公共逻辑
mixins 用于在 Vue 中便捷复用变量、方法、组件引用、生命周期等 使用方法 创建文件myMixin.js export const myMixin {data() {return {webName: 朝阳的博客}},created() {alert(欢迎来到${this.webName})},methods: {hi() {alert(欢迎来到${this.webName})}} }vue文件中引入…...

ArrayList的常用方法
ArrayList是Java中常用的动态数组类,它提供了一系列用于操作和管理数组的方法。下面是一些ArrayList常用方法的介绍: add()方法:向ArrayList中添加元素,可以指定位置添加元素或者在末尾添加元素。 ArrayList<String> list …...

ES-Hadoop:将Elasticsearch与Hadoop无缝集成的开源工具
hadoop 大数据技术之Hive(3)PyHive pyhdfs ES,Elasticsearch https://zhuanlan.zhihu.com/p/595505475?utm_id0 Hadoop hdfs 、hive、spark https://blog.51cto.com/u_16099278/6901638 ES-Hadoop:将Elasticsearch与Hadoop无缝集成的开源工…...

质量模型、软件测试流程和测试用例
质量模型 衡量一个优秀软件的维度 可以从功能性、性能、兼容性、易用性、安全、可靠性、可维护性、可移植性这几个方面去做软件测试,但咱们在正常测试中一般是选取前五项进行测试 测试流程 1、需求评审:确保各部门对需求的理解一致 2、测试计划编写&a…...
集简云新增“文本语音转换”功能,实现智能语音交互
为丰富人工智能领域的应用集成,为用户提供更便捷和智能化的信息获取和视觉创作方式,本周集简云上线了内置应用—文本语音转换。目前支持OpenAI TTS和TTS HD模型,实现文本语音高效智能转换,也可根据你的产品或品牌创建独特的神经网…...

图像处理领域专业术语
图像处理中的一些常见术语,涵盖了从基础概念到高级处理技术的各个方面。 以下是一些图像处理领域常用的专业术语及其解释: 像素(Pixel): 图像的最基本单元,每个像素都有一个或多个与其关联的数值࿰…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
