数据结构(三)复杂度的深层次剖析
之前发布了数据结构(一),很多同学反响不够清晰,那今天就发一篇对复杂度专题的博客,希望对大家理解复杂度提供一些帮助。
时间复杂度
我们先来一个理解一个复杂度,二分查找的复杂度(之前写过二分查找的专题博客,感兴趣的可以看一看) CSDN![]() https://mp.csdn.net/mp_blog/creation/editor/135742310
https://mp.csdn.net/mp_blog/creation/editor/135742310
我们在数据结构(一)中讲解了,但是没有画图,现在为了方便大家的理解现在我重新讲解一下。
我们先把代码拿出来看看
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n-1;
// [begin, end]:begin和end是左闭右闭区间,因此有=号
while (begin <= end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid-1;
else
return mid;
}
return -1;
}这时候大家会好奇该如何计算其复杂度,其实搞清楚原理也比较容易理解。
二分查找的原理就不在过多的讲解了,不懂的小伙伴可以去看看上面的链接。
我们还是老样子画图来为大家演示:



当我们在不断地缩减,直到缩减到只剩下一个值的时候。

那么这就是最坏的一个情况,如果这个值是我们想要找的那个值,那么就找到了,如果不是那么我们输出找不到。
随之而来的疑问就是,我们一共找了多少次呢?
假设我们有N个值,我们每次都缩减一半,那么就是N/2,这是一次。那么我们一共找了多少次呢?
N/2/2/2/2/2/2.............=1 直到我们找到那个数为止。 这是最坏情况,那么我们除了多少个2呢?
不难看出,其实我们找了多少次就除了多少个2。
关键点拨:假设我找了X次,那么我们 就可以得到表达式。
第一步:N/2/2/2/2/2/2/2...............=1
第二步:N=1*2^x (等式两边同时乘2)
第三步:2^x=N
第四步:化简

基本操作执行最好1次,最坏O(logN)次,时间复杂度为 O(logN) ps:logN在算法分析中表示是底
数为2,对数为N。有些地方会写成logN 。(由于对数在键盘中不好敲出来,所以我们通常省略2)。
补充时间复杂度例题:
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{
if(0 == N)
return 1;
return Fac(N-1)*N;
}大家看到这串代码时一定有想骂街的冲动,但是有我在大家不用担心,我来为大家搞定它。

那么开始进入正题:
上面的代码是 N 的阶乘的原码,之前我的博客也写过,感兴趣的小伙伴可以去看看地址就放在这里了-用C语言实现阶乘的相加-CSDN博客文章浏览阅读373次,点赞11次,收藏9次。i=3 ret=1*2*3 此时的ret=6 可以理解为1*2*3。i=2 ret=1*2 此时ret=2 可以理解为1*2。当n=2时ret=1*2 同样把值存在sum中 此时的ret=2。ret开始变化 例如:当for循环运行到i=3时,i=1 ret=1*1 此时ret=1。那么我们有没有其他方案呢,答案是有的我们可以这样在求2的阶乘时直接在1的阶乘上乘2 1*2。关键点拨:ret=ret*n 当n=1时ret=1*1 并把值存在sum中。https://blog.csdn.net/weixin_73496371/article/details/135739915。
这里我们就直接开始,我们先思考一个问题,阶乘调用了多少次函数?
老样子画图解释:

我们不断调用FAC从N次到N-1次再到N-2次...........直到0次
我们把它们相加起来就可以得到。
计算分析发现基本操作递归了N次,时间复杂度为O(N)。
我们再来看难度比较大的一道题:
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}斐波那契我们用简单的图片来理解一下

理解起来有点像细胞分化的意思。
那么问题来了,一共有多少次调用呢?有个简易的方法来看一下

我们观察最左边的数 2^0 2^1 2^2 2^3..........它们实际上是一个等比数列。
我们使用等比数列求和的方式求和. 这就用到了我们的高中知识。

通过计算分析发现基本操作递归了2^N次,时间复杂度为O(2^N)。
接下来为大家详解空间复杂度
空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
实例1:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}结论: 实例1使用了常数个额外空间,所以空间复杂度为 O(1)
解释:空间复杂度是我们一个算法在运行时额外(由于逻辑的需要)开辟的空间。
上述代码算法(排序过程)额外开辟的有 size_t end size_t i exchange它们开辟的空间都是常数,所以使用大O渐进法不难算出空间复杂度。 O(1)
如果大家对这道题有疑问的话我们再来看一道题,相信你的问题不在是问题了。

实例2:
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if(n==0)
return NULL;
long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}我们观察在算法的运行中只动态开辟了(n+1)的空间。 ---------malloc((n+1)
那么我们使用大O渐进表示法:
动态开辟了N个空间,空间复杂度为 O(N)。
到这里我想大家对空间复杂度有了全新的理解了吧。
常见复杂度对比
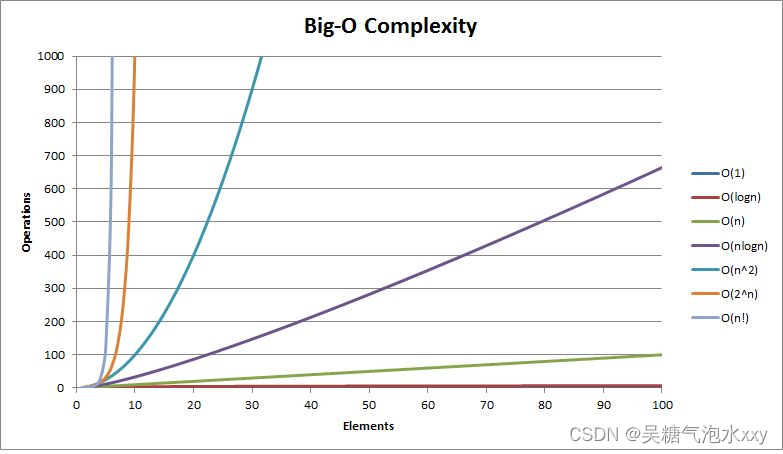
一般算法常见的复杂度如下:

复杂度的oj练习
消失的数字OJ链接:. - 力扣(LeetCode). - 备战技术面试?力扣提供海量技术面试资源,帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。![]() https://leetcode-cn.com/problems/missing-number-lcci
https://leetcode-cn.com/problems/missing-number-lcci
感谢你的观看
后续更新更多数据结构的相关知识
相关文章:
数据结构(三)复杂度的深层次剖析
之前发布了数据结构(一),很多同学反响不够清晰,那今天就发一篇对复杂度专题的博客,希望对大家理解复杂度提供一些帮助。 时间复杂度 我们先来一个理解一个复杂度,二分查找的复杂度(之前写过二…...
JavaWeb -- HTTP -- WEB服务器TOMCAT
一.HTTP介绍: HTTP(Hyper Text Protocol) 实际上是一种超文本传输的协议,规定了浏览器跟服务器之间的一些数据传输的规则 例如B/S 对于浏览器的请求,以及相应服务器的响应,都必须依靠这种协议,规范,才能够彼此之间相互 理解 HTTP的协议特点: 1.基于TCP协议: 面向连接 更加安全…...

GitHub与Git命令使用笔记
GitHub与Git命令使用笔记 文章目录 GitHub与Git命令使用笔记上传本地的新项目到github1. 创建新的GitHub仓库2. 初始化本地项目目录3. 将本地仓库关联到GitHub4. 推送本地代码到GitHub上传本地项目到GitHub时发生冲突 将默认分支名称从master改为maingit 把远程项目拉到本地&am…...
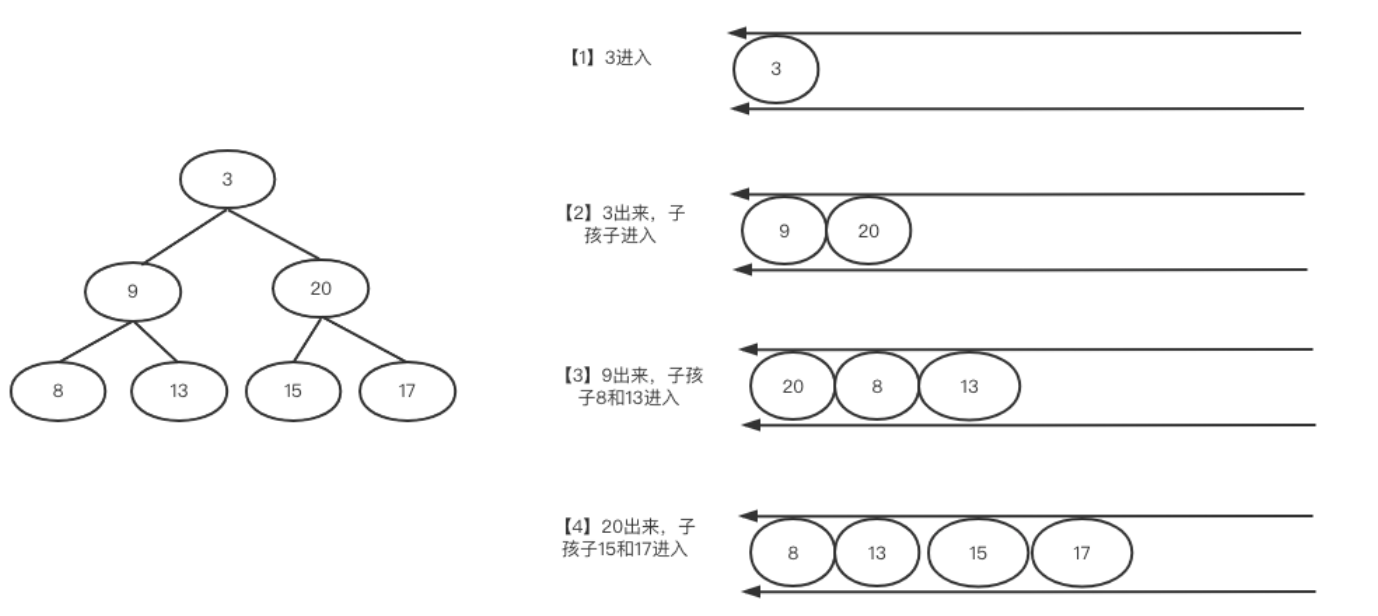
二叉树的层次遍历经典问题-算法通关村
二叉树的层次遍历经典问题-算法通关村 1 层次遍历简介 广度优先在面试里出现的频率非常高,整体属于简单题。广度优先又叫层次遍历,基本过程如下: 层次遍历就是从根节点开始,先访问根节点下面一层全部元素,再访问之后…...

SQLiteC/C++接口详细介绍sqlite3_stmt类(十二)
返回:SQLite—系列文章目录 上一篇:SQLiteC/C接口详细介绍sqlite3_stmt类(十一) 下一篇: SQLiteC/C接口详细介绍sqlite3_stmt类(十三) 48、sqlite3_stmt_isexplain sqlite3_stmt_is…...

大模型时代如何做安全?
现在应该没人怀疑AI时代的到来了吧,在HUB上每天100的新的预训练模型产生,不夸张的说的,现在稍微有点计算机基础的人都可以训练自己的模型了。 说远了,还是说说那些不争气的安全厂商吧。为啥只说安全厂商?因为国内还是…...

新型储能是什么,储能系统解决方案现状及趋势详细说明
新型储能是指新兴的能够存储电能并在需要时释放的储能技术。其中主要包括光伏储能和商业储能。 光伏储能是指通过光伏电池将太阳能转化为电能,并将其存储起来以供后续使用。光伏储能系统一般由太阳能电池板、储能装置和逆变器组成。光伏储能可以将白天产生的电能存…...
)
掌握Go语言:Go语言中的字典魔法,高效数据检索与应用实例解析(18)
在Go语言中,字典通常指的是map类型,它是一种用于存储键值对的数据结构。字典在Go中非常常见,是一种高效的数据结构,用于快速查找和检索数据。 字典的详细使用方法 创建字典 可以使用make函数来创建字典,并指定键值对…...

Flutter-仿携程首页类型切换
效果 唠叨 闲来无事,不小心下载了携程app,还幻想可以去旅游一番,奈何自己运气不好,自从高考时第一次吹空调导致自己拉肚子考试,物理,数学考了一半就交卷,英语2B铅笔除了问题,导致原…...

C语言 自定义类型:结构体
目录 前言 一、结构体类型 1.1 结构体的声明 1.2 结构体变量的创建和初始化 1.3 结构体的特殊声明 1.4 结构体的自引用 二、结构体的对齐 2.1 对齐规则 2.2 内存对齐的原因 2.3 修改默认对齐数 2.4 结构体传参 三、结构体实现位段 3.1 位段的内存分配 3.2 段的跨平…...

计算机网络拓扑结构
目录 <网络拓扑结构概念> <典型的拓扑结构介绍> 第一种,总线型网络拓扑结构 第二种,星型网络拓扑结构 第三种,树型网络拓扑结构 第四种,环型网络拓扑结构 第五种,网状型网络拓扑结构 第六种&#…...

FPGA通过I2C控制AT24C64
文章目录 前言一、代码设计框图二、IIC_drive模块设计2.1、模块接口:2.2、代码功能描述:2.3、IIC协议实现过程: 三、EEPROM_ctrl模块设计3.1、模块接口:3.2、代码功能描述 四、EEPROM_drive模块五、iic_top模块 前言 继上一篇FPG…...
134. 加油站(力扣LeetCode)
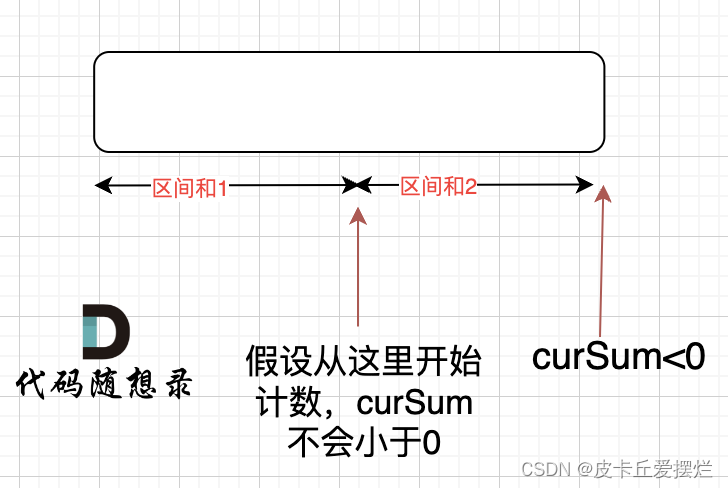
文章目录 134. 加油站题目描述暴力枚举(超时)代码一代码二(优化) 贪心算法方法一方法二 134. 加油站 题目描述 在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车&…...

XSKY 智能存储,助力“数据要素 X”先进制造
3 月 21-22 日,主题为“突破 智行”的 IMC2024 第七届中国智造数字科技峰会在重庆召开。作为在先进制造领域拥有领先存储解决方案以及众多应用实践的企业,星辰天合受邀参加了此次峰会并荣获大会颁发的“最佳存储解决方案奖”。同时,星辰天合先…...

数据挖掘与分析学习笔记
一、Numpy NumPy(Numerical Python)是一种开源的Python库,专注于数值计算和处理多维数组。它是Python数据科学和机器学习生态系统的基础工具包之一,因为它高效地实现了向量化计算,并提供了对大型多维数组和矩阵的支持…...

linux docker镜像初始化
linux docker镜像初始化 简介 有的镜像内部使用的linux系统特别精简,许多常用命令无法安装,导致排查问题较为困难。 可以使用cat /etc/os-release查看容器使用的linux版本,再进行一些常用操作的初始化。 Debian # 设置镜像源 RUN rm -f /…...

专业140+总分410+南京大学851信号与系统考研经验南大电子信息与通信集成,电通,真题,大纲,参考书。
今年分数出来还是有点小激动,专业851信号与系统140(感谢Jenny老师辅导和全程悉心指导,答疑),总分410,梦想的南大离自己越来越近,马上即将复试,心中慌的一p,闲暇之余&…...

. ./ bash dash source 这五种执行shell脚本方式 区别
实际上,., ./, bash, dash, source 是五种不同的方式来执行 shell 脚本,它们之间有一些区别。 .(点号)或 source 命令:这两个命令是等价的,它们都是 Bash shell 内置的命令。它们用于在当前 shell 环境中执行脚本。当使用 . script.sh 或 source script.sh 命令来执行脚本…...

【React 】React 性能优化的手段有哪些?
1. 是什么 React凭借virtual DOM和diff算法拥有高效的性能,但是某些情况下,性能明显可以进一步提高 在前面文章中,我们了解到类组件通过调用setState方法,就会导致render ,父组件一旦发生render渲染,子组件一定也会执…...
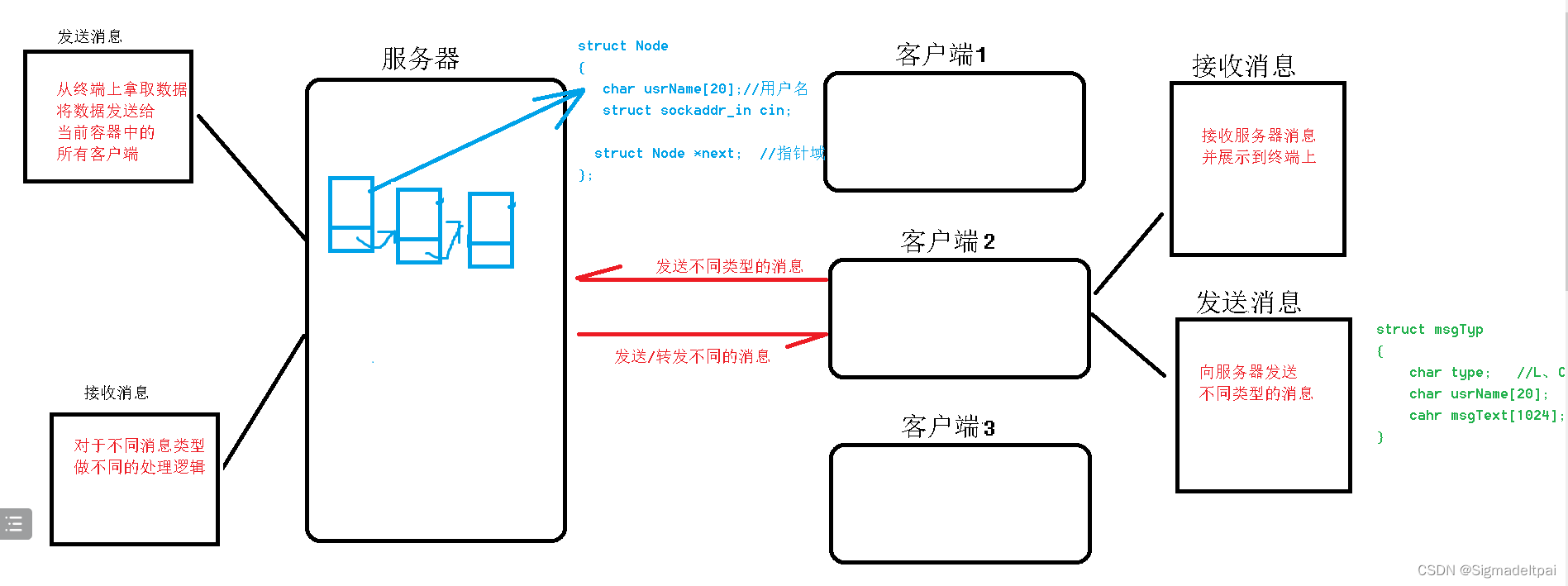
3.22网络编程小项目
基于UDP的网络聊天室 项目需求: 如果有用户登录,其他用户可以收到这个人的登录信息如果有人发送信息,其他用户可以收到这个人的群聊信息如果有人下线,其他用户可以收到这个人的下线信息服务器可以发送系统信息 服务器 #includ…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
