LeetCode---126双周赛
题目列表
3079. 求出加密整数的和
3080. 执行操作标记数组中的元素
3081. 替换字符串中的问号使分数最小
3082. 求出所有子序列的能量和
一、求出加密整数的和

按照题目要求,直接模拟即可,代码如下
class Solution {
public:int sumOfEncryptedInt(vector<int>& nums) {int n=nums.size(),res=0;for(auto x:nums){int s = 0, mx = 0;while(x){mx=max(mx,x%10);s=s*10+1;x/=10;}res+=mx*s;}return res;}
};二、执行操作标记数组中的元素

题目不难,依旧还是只需要模拟,但是代码量不少,要细心,思路如下:
对于每次查询的操作1:只要判断垓下标是否被标记,然后处理即可
对于每次查询的操作2:要把没有标记过的最小的k个数字标记,如果数字相同则下标小的先标记,很显然要排序(两个维度的排序---首先比较数值,其次比较下标),这里讲一个技巧:我们没必要将数值和下标打包在一起(即用pair)排序,我们可以直接对下标进行排序,具体看代码
如何表示一个数是否被标记?可以额外开一个数组,也可以直接在原数组上修改,将标记过的数记为-1
代码如下
class Solution {
public:vector<long long> unmarkedSumArray(vector<int>& nums, vector<vector<int>>& queries) {int n = nums.size(), m = queries.size();vector<long long> ans(m);vector<int>idx(n);long long s = 0;for(int i=0;i<n;i++) {idx[i]=i;s+=nums[i];}sort(idx.begin(),idx.end(),[&](int x,int y){return nums[x]!=nums[y]?nums[x]<nums[y]:x<y;});for(int i=0,j=0;i<m;i++){const auto& v = queries[i];int index = v[0], k = v[1];if(nums[index]>=0){s -= nums[index];nums[index] = -1;}while(k&&j<n){if(nums[idx[j]]<0){j++;continue;}s -= nums[idx[j]];nums[idx[j]]=-1;j++,k--;}ans[i]=s;}return ans;}
};三、替换字符串中的问号使分数最小

这题是思维题:
首先我们要明白字母出现的顺序并不会影响它们对总分数的贡献(因为字母对分数的贡献仅仅只和该字母出现的次数有关,字母与其他字母之间是相互独立的),也就是说我们只要考虑每个 '?' 填哪个字母即可,根据cost的定义,我们优先考虑之前出现次数少的字母对 '?' 进行填充,当出现次数一样少时,我们优先考虑字典序小的字母,然后对选出的字母进行排序,最后按照 '?' 的位置进行替换即可。
代码如下
class Solution {
public:string minimizeStringValue(string s) {int n = s.size();string tmp;int cnt[26] = { 0 },c = 0;for(const auto& e:s){if(e!='?') cnt[e-'a']++;else c++;}auto cmp=[](const pair<int,int>& x,const pair<int,int>& y)->bool{return x.first!=y.first ? x.first > y.first : x.second > y.second;};priority_queue<pair<int,int>,vector<pair<int,int>>,decltype(cmp)> pq(cmp); //小堆for(int i=0;i<26;i++)pq.push({cnt[i],i});while(c--){auto [x,ch] = pq.top();pq.pop();pq.push({x+1,ch});tmp += 'a'+ch;}sort(tmp.begin(),tmp.end());for(int i=0,j=0;i<n;i++){if(s[i]=='?')s[i]=tmp[j++];}return s;}
};四、求出所有子序列的能量和
 这题找子序列中的子序列,看着很绕,其实就是找和为k的子序列能出现在多少个子序列中,即和为k的子序列做出的贡献,拿示例一举例:和为3的子序列有[1,2]和[3],其中[1,2]在2个子序列中出现,[3]在4个子序列中出现,所以答案为2+4=6。很显然每个和为3的子序列的贡献为2^(n-L),其中n为整个数组的长度,L为子序列的长度。
这题找子序列中的子序列,看着很绕,其实就是找和为k的子序列能出现在多少个子序列中,即和为k的子序列做出的贡献,拿示例一举例:和为3的子序列有[1,2]和[3],其中[1,2]在2个子序列中出现,[3]在4个子序列中出现,所以答案为2+4=6。很显然每个和为3的子序列的贡献为2^(n-L),其中n为整个数组的长度,L为子序列的长度。
故答案的表达式为 sum(2^(n-L) * num_K_L) 1<=L<=n,num_K_L表示长为L,和为K的子序列个数
如何求长为L,和为K的子序列的个数?
这是一个背包问题,限制条件有两个:1、长为L 2、和为K
设f[i][L][c]表示前i个数中,长为L,和为c的子序列的个数
1、如果当前的数不在和为c的子序列中,则f[i][L][c]=f[i-1][L][c]
2、如果当前的数在和为c的子序列中,则f[i][L][c]=f[i-1][L-1][c-nums[i]]
所以f[i][L][c]=f[i-1][L][c]+f[i-1][L-1][c-nums[i-1]]
初始化:f[i][0][0]=1,因为长为0,和为0的子序列只能是空,只有一个
代码如下
class Solution {
public:int sumOfPower(vector<int>& nums, int k) {int n=nums.size();const int MOD = 1e9+7;int f[n+1][n+1][k+1];memset(f,0,sizeof(f));//f[i][L][j] = f[i-1][L][j] + f[i-1][L-1][j-nums[i]]for(int i=0;i<=n;i++)f[i][0][0]=1;for(int i=0;i<n;i++){for(int j=1;j<=k;j++){for(int L=1;L<=i+1;L++){f[i+1][L][j] = (f[i][L][j] + (j>=nums[i]?f[i][L-1][j-nums[i]]:0))%MOD;}}}long long ans = 0, pow2 = 1;for(int i=n;i>0;i--){ans = (ans + f[n][i][k]*pow2)%MOD;pow2 = pow2*2%MOD;}return ans%MOD;}
};// 优化空间
class Solution {
public:int sumOfPower(vector<int>& nums, int k) {int n=nums.size();const int MOD = 1e9+7;int f[n+1][k+1];memset(f,0,sizeof(f));f[0][0]=1;for(int i=0;i<n;i++){for(int j=k;j>=nums[i];j--){for(int L=1+i;L>0;L--){f[L][j] = (f[L][j] + f[L-1][j-nums[i]])%MOD;}}}long long ans = 0, pow2 = 1;for(int i=n;i>0;i--){ans = (ans + f[i][k]*pow2)%MOD;pow2 = pow2*2%MOD;}return ans%MOD;}
};当然我们也可以根据题目直接定义状态:f[i][j]表示前i个数为数组的,元素和为k的能量值
1、如果nums[i]不在子序列和为k的序列中,那么它有选和不选两种可能,f[i+1][j]=f[i][j]*2
2、如果nums[i]在子序列和为k的序列中,那么它只能被选,f[i+1][j]=f[i][j-nums[i]]
举个例子[1,2,3],要求和为3,假设遍历到 i = 2 ,如果nums[i]=3不在我们想要的子序列中,那么它可以选,也可以不选,即f[i][j] * 2,如果nums[i]=3在我们想要的子序列中,那么它只能被选,即f[i][j-nums[i]]
所以状态转移方程为 f[i+1][j]=f[i][j] * 2+ f[i][j-nums[i]]
代码如下
class Solution {
public:int sumOfPower(vector<int>& nums, int k) {const int MOD=1e9+7;int n=nums.size();vector<vector<long long>>f(n+1,vector<long long>(k+1));f[0][0]=1;for(int i=0;i<n;i++){for(int j=0;j<=k;j++){f[i+1][j]=(f[i][j]*2+(j>=nums[i]?f[i][j-nums[i]]:0))%MOD;}}return f[n][k];}
};//优化空间
class Solution {
public:int sumOfPower(vector<int>& nums, int k) {const int MOD=1e9+7;int n=nums.size();vector<long long>f(k+1);f[0]=1;for(int i=0;i<n;i++){for(int j=k;j>=0;j--){f[j]=(f[j]*2+(j>=nums[i]?f[j-nums[i]]:0))%MOD;}}return f[k];}
};相关文章:

LeetCode---126双周赛
题目列表 3079. 求出加密整数的和 3080. 执行操作标记数组中的元素 3081. 替换字符串中的问号使分数最小 3082. 求出所有子序列的能量和 一、求出加密整数的和 按照题目要求,直接模拟即可,代码如下 class Solution { public:int sumOfEncryptedInt…...

[python] ETL 工作流程 Prefect
Prefect 是一个用于构建、调度和监控数据流程的 Python 库。它提供了一种简单而强大的方式来管理 ETL(Extract, Transform, Load)工作流程。下面是一个简单的示例,演示了如何使用 Prefect 来创建和运行一个简单的任务: 首先&…...
html第一次作业
常用标签 0, 骨架(!tap) <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><t…...
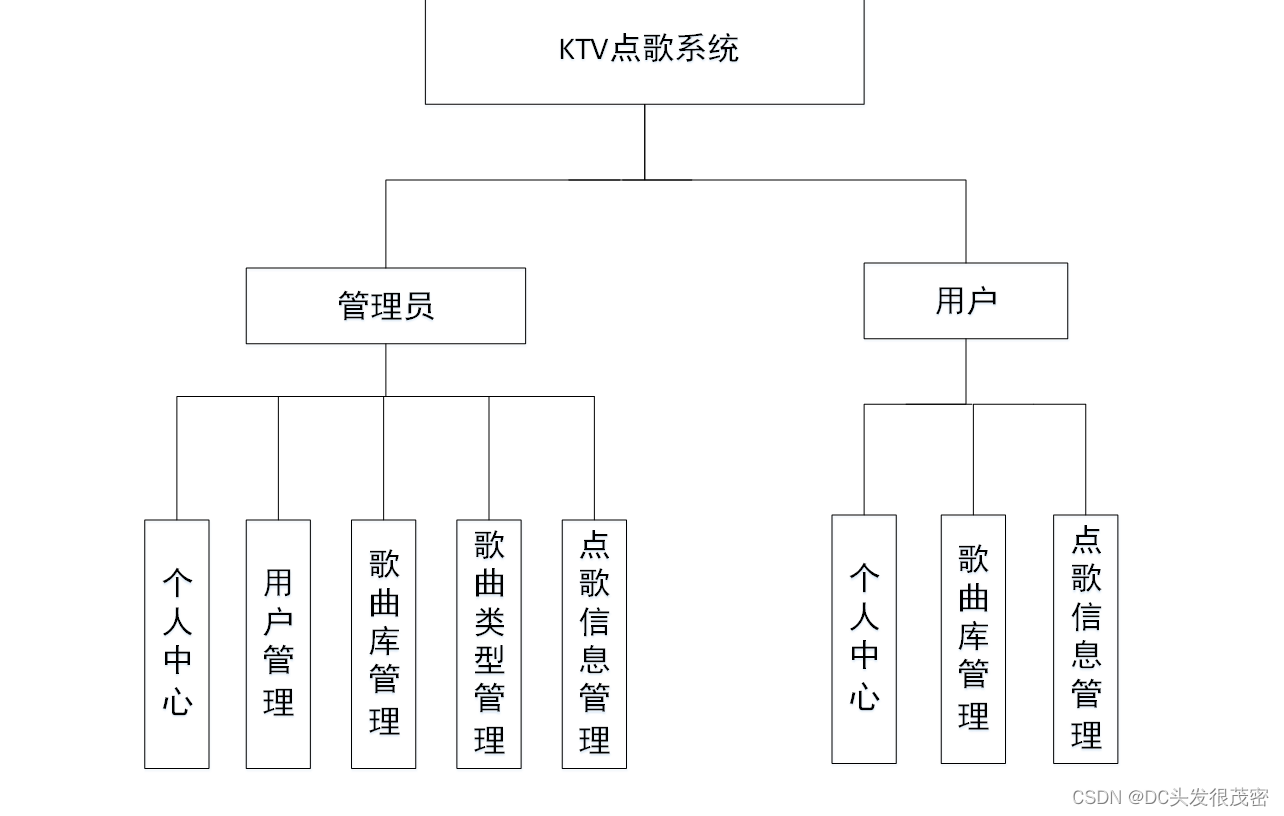
基于java实现的KTV点歌系统
开发语言:Java 框架:ssm 技术:JSP JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件:eclipse/myeclip…...

GPT+向量数据库+Function calling=垂直领域小助手
引言 将 GPT、向量数据库和 Function calling 结合起来,可以构建一个垂直领域小助手。例如,我们可以使用 GPT 来处理自然语言任务,使用向量数据库来存储和管理领域相关的数据,使用 Function calling 来实现领域相关的推理和计算规…...
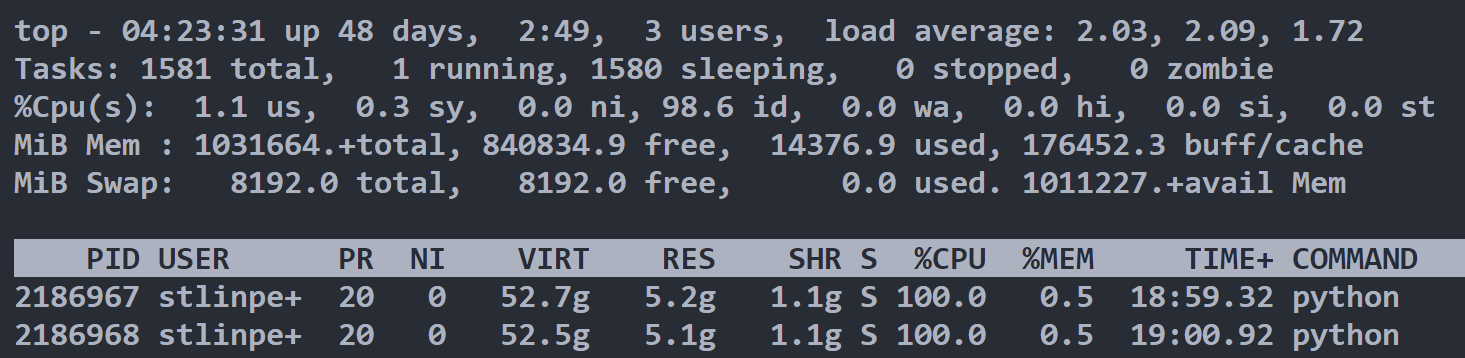
DeepSeek-coder 微调训练记录
简介 微调过程不再细说, 参考link进行即可. 主要是数据集. 1.3b模型微调训练占用资源信息 top信息 评估 根据DeepSeek-coder的Evaluation试进行对微调后的模型进行评估. 其中的评估库主要是evol-teacher和human-eval. 新建一个eval_ins.sh文件, 填入以下内容 LANG"…...
)
【Android】【Bluetooth Stack】蓝牙音乐协议分析之音频控制与信息加载(超详细)
1. 精讲蓝牙协议栈(Bluetooth Stack):SPP/A2DP/AVRCP/HFP/PBAP/IAP2/HID/MAP/OPP/PAN/GATTC/GATTS/HOGP等协议理论 2. 欢迎大家关注和订阅,【蓝牙协议栈】和【Android Bluetooth Stack】专栏会持续更新中.....敬请期待! 目录 1. 音乐信息加载 1.1 歌曲信息 1.1.1 key_c…...
ChatGPT无法登录,提示我们检测到可疑的登录行为?如何解决?
OnlyFans 订阅教程移步:【保姆级】2024年最新Onlyfans订阅教程 Midjourney 订阅教程移步: 【一看就会】五分钟完成MidJourney订阅 GPT-4.0 升级教程移步:五分钟开通GPT4.0 如果你需要使用Wildcard开通GPT4、Midjourney或是Onlyfans的话&am…...

程序员表白
啥?!你说程序员老实,认真工作,根本不会什么表白!那你就错了!(除了我) 那今天我们就来讲一下这几个代码!赶紧复制下来,这些代码肯定有你有用的时候! 1.Python爱心代码 im…...

CSS的使用与方法
什么是CSS CSS是层叠样式表。它是一种用于描述网页或者文档外观和样式的标记语言。 层级样式表:就是给HTML标签加样式的。 如果说HTML是个游戏英雄 、那么CSS就是游戏皮肤。 【一】注释语法 /* 注释 */ 【二】CSS的语法结构 选择符 {样式属性: 样式属性值;样…...
离线安装mongoDB集群)
(保姆级)离线安装mongoDB集群
Docker搭建MongoDB集群 副本集模式(Replica Set) 是一种互为主从的关系, Replica Set 将数据复制多份保存,不同服务器保存同一份数据,在出现故障时自动切换,实现故障转移。 此集群拥有一个主节点和多个从…...
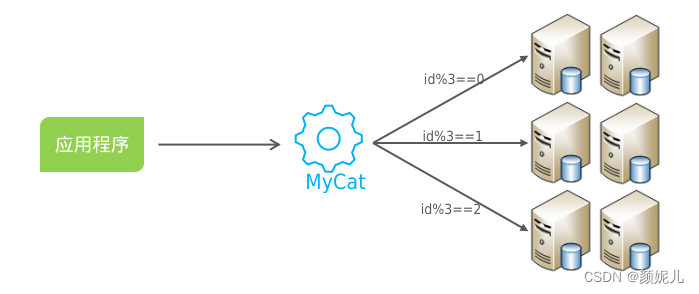
面试笔记——MySQL(主从同步原理、分库分表)
主从同步原理 主从同步结构:主库负责写数据,从库负责读数据,如图—— MySQL主从复制的核心就是二进制日志(BINLOG),它记录了所有的 DDL(数据定义语言)语句和 DML(数据操…...

面试题2.0
目录 css 动画 深拷贝和浅拷贝 ES6新特性 事件循环 vue-router原理 flex布局 session和local storage分别是用来干嘛的? http状态码 原型链 虚拟dom vuex的五个属性 vue路由跳转的四种方式 vue生命周期 link和import的区别 GET 与 POST 的区别 fle…...
(优先队列+快排+快速选择))
【剑指offer】53. 最小的k个数(java选手)(优先队列+快排+快速选择)
题目链接 题目链接 力扣题目链接 题目描述 输入 n个整数,找出其中最小的 k 个数。 注意: 输出数组内元素请按从小到大顺序排序; 数据范围 1≤k≤n≤1000 样例 输入:[1,2,3,4,5,6,7,8] , k4 输出:[1,2,3,4] 题目分析 排序算法…...
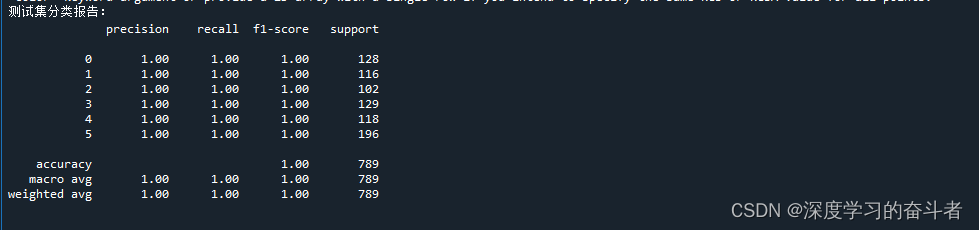
带有GUI界面的电机故障诊断(MSCNN-BILSTM-ATTENTION模型,TensorFlow框架,有中文注释,带有六种结果可视化)
本次创作最主要是在MSCNN-BILSTM-ATTENTION模型(可轻松替换为其它模型)基础上,搭建GUI测试界面,方便对你想要测试的数据的进行测试,同时进行了全面的结果可视化:1.训练集和测试集的准确率曲线,2…...
【技术栈】Spring Cache 简化 Redis 缓存使用
SueWakeup 个人主页:SueWakeup 系列专栏:学习技术栈 个性签名:保留赤子之心也许是种幸运吧 本文封面由 凯楠📸 友情提供 目录 本栏传送门 1. Spring Cache 介绍 2. Spring Cache 常用注解 注:手机端浏览本文章…...
 got an unexpected keyword argument ‘ciphers‘)
解决wrap_socket() got an unexpected keyword argument ‘ciphers‘
看报错本以为是一个简单的传参问题,没想到查到盘丝洞。 # 报错信息 wrap_socket() got an unexpected keyword argument ciphers# 报错代码段 _exception_handler() def connect(self):u"""连接MySQL数据库"""self.config_connect_a…...

【力扣hot100】128.最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1: 输入:nums [100,4,200,1,3,2] 输出:4 解…...

css的text-shadow详解
CSS的text-shadow属性用于为文本添加阴影效果,以增强文本的立体感和印刷品质感。该属性可以接受多个值,每个值通过空格分隔,以定义阴影的各个方面。以下是text-shadow属性的详细介绍: 阴影颜色 (Color): 这是阴影的颜色值。它可以…...

Qt 利用共享内存实现一次只能启动一个程序(单实例运行)
Qt 利用共享内存实现一次只能启动一个程序 文章目录 Qt 利用共享内存实现一次只能启动一个程序摘要利用共享内存实现一次只能启动一个程序示例代码 关键字: Qt、 unique、 单一、 QSharedMemory、 共享内存 摘要 今天接着在公司搞我的屎山代码,按照…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
