【机器学习-05】模型的评估与选择
在前面【机器学习-01】机器学习基本概念与建模流程的文章中我们已经知道了机器学习的一些基本概念和模型构建的流程,本章我们将介绍模型训练出来后如何对模型进行评估和选择等
1、 误差与过拟合
学习器对样本的实际预测结果与真实值之间的差异,我们称之为误差(error)。这个误差在训练集上表现出来的是训练误差(training error),也称为经验误差(empirical error);而在测试集上则是测试误差(test error)。而当我们希望学习器在新样本上也能有良好表现时,需要关注的是其泛化误差(generalization error),即学习器在所有新样本上的误差。
在学习过程中,存在两种可能的问题。一种是学习器对训练集的学习过于深入,以至于把训练样本中的某些特殊性质也当作了普遍规律,这种情况我们称之为过拟合(overfitting)。另一种则是学习器的学习能力不足,连训练集的基本特征都没有完全掌握,这种情况我们称之为欠拟合(underfitting)。
在过拟合的情况下,虽然训练误差很小,但测试误差却可能很大,因为学习器过于依赖训练样本的特殊性质,而无法很好地泛化到新样本。而在欠拟合的情况下,由于学习器连训练集的基本特征都没有学好,因此无论是训练误差还是测试误差都会比较大。
虽然欠拟合问题相对容易解决,例如通过增加迭代次数等方法,但过拟合问题却是机器学习领域面临的一大挑战。目前,我们还没有找到一种完美的解决方案来完全避免过拟合的发生。因此,在机器学习的实践中,我们需要时刻警惕过拟合的可能性,并采取相应的措施来尽可能减少其影响。
2 、评估方法
在现实应用中,我们面临着多种算法的选择,如何确定哪个算法最适合我们的任务呢?我们的目标是找到泛化误差最小的学习器,因为泛化误差可以反映模型在新样本上的性能。但问题是,泛化误差是无法直接获得的,因为它涉及到模型在未知数据上的表现。
为了解决这个问题,我们通常会采用一个与训练集相互独立的“测试集”来评估学习器对新样本的判别能力。我们将测试集上的“测试误差”作为“泛化误差”的一个近似值。这里的关键是,测试集应该尽可能不与训练集重叠,以保证评估的公正性和准确性。
举个例子来说明这个道理:假设老师出了10道练习题供学生们练习,但如果考试的时候还是用这同样的10道题,那么有些学生可能只会做这10道题却能得高分。这样的成绩显然不能真实反映学生的水平。同样地,如果我们用与训练集相同的样本进行测试,那么得到的评估结果就会过于乐观,无法真实反映模型的泛化能力。因此,我们需要一个独立的测试集来评估模型,就像考试需要独立于练习题的试题一样。这样才能更准确地评估模型的性能,选择出最适合我们任务的学习算法。
3、 训练集与测试集的划分方法
如上所述,为了使用“测试集”的“测试误差”来近似“泛化误差”,我们需要对初始数据集进行科学的划分,从而得到相互独立的“训练集”和“测试集”。下面,我们将介绍几种常用的数据集划分方法,这些方法都有助于我们更加准确地评估模型的性能。
3.1 留出法(hold-out)
我们将数据集D分割为两个互不重叠的集合:训练集S和测试集T。这两个集合应满足D=S∪T且S∩T=∅,确保它们之间没有交集。常见的划分比例是,大约2/3到4/5的样本用于训练,而剩下的样本则用于测试。在此过程中,我们要特别注意保持训练集和测试集中数据分布的一致性,避免由于分布差异而引入不必要的偏差。一种常用的做法是采用分层抽样方法。然而,由于划分的随机性,单次划分的结果可能不够稳定。因此,通常我们会进行多次随机划分,并重复实验以获取平均值,从而得到更可靠和稳定的结果。
3.2 交叉验证法
我们将数据集D分割为k个大小相等且互不重叠的子集,确保它们的并集仍为D,且任意两个子集之间无交集。为了保持数据分布的一致性,我们采用分层抽样的策略进行子集的划分。交叉验证法的核心思想在于:每次从k个子集中选择k-1个作为训练集,而剩下的那个子集则作为测试集。这样的划分方式共有k种,因此我们可以进行k次独立的训练和测试。最终,我们将这k次测试的结果取平均值,以得到一个更为稳定和可靠的评估结果。这种方法通常被称为“k折交叉验证”,其中k最常见的取值为10。在下图中,我们给出了10折交叉验证的直观示意图,以便更好地理解这一过程。

与留出法相似,K折交叉验证在划分数据集D为K个子集时也存在随机性。因此,为了提高评估的稳定性,我们通常会进行p次K折交叉验证,这被称为p次k折交叉验证。一个常见的做法是进行10次10折交叉验证,即总共进行100次独立的训练/测试过程。特别地,当我们将数据集D划分为K个子集,且每个子集中仅包含一个样本时,这种方法被称为“留一法”。尽管留一法的评估结果通常更为准确,但由于其计算成本巨大,对计算机资源的消耗也相当显著。
3.3 自助法
我们的目标是评估使用完整数据集D训练出的模型性能。然而,在留出法和交叉验证法中,由于需要保留部分样本作为测试集,实际用于训练的样本规模会小于D,这可能导致因训练样本大小差异而产生的估计偏差。留一法虽然在一定程度上减少了这种影响,但其计算成本过高。为了解决这个问题,我们引入了“自助法”。
自助法的核心思路是这样的:从包含m个样本的数据集D中,我们反复执行以下步骤m次:每次随机挑选一个样本,将其复制到新的数据集D’中,然后将该样本放回原数据集D。这样,经过m次操作后,我们得到了一个同样包含m个样本的数据集D’。值得注意的是,由于样本在每次挑选后都会被放回,因此同一个样本可能在D’中出现多次,也可能一次都不出现。经过计算,我们可以得知在m次采样过程中,某个样本始终不被选中的概率随着m的增大而趋近于一个特定的值。
lim m → ∞ ( 1 − 1 m ) m ⟶ 1 e ≈ 0.368 { \lim_{m\to\infty} \left( 1-\frac{1}{m} \right)^m \longrightarrow\frac{1}{e}\approx0.368 } m→∞lim(1−m1)m⟶e1≈0.368
通过自助采样法,我们可以从初始样本集D中构建一个新的数据集D’,同时保留那些未出现在D’中的样本作为测试集。由于自助采样的随机性,大约36.8%的初始样本将不会出现在D’中,因此这些未被选中的样本可以构成测试集D-D’。自助法在数据集较小,难以有效划分训练集和测试集时尤为实用。然而,需要注意的是,由于自助法是通过随机抽样来构建数据集的,这可能会改变原始数据集的分布,从而引入一定的估计偏差。因此,在初始数据集足够大且易于划分时,留出法和交叉验证法通常更为常用。
4、 调参
学习算法中往往存在需要设定的参数(parameter) ,这些参数的取值对于模型性能的影响至关重要,我们通常称之为“调参”(parameter tuning)。由于很多参数的取值范围可能非常广泛,完全遍历所有可能取值是不现实的。因此,一种常见的做法是为每个参数设定一个合理的取值范围和步长,这样我们就可以在有限的时间内进行有效的参数调整。
例如,假设我们有一个算法包含三个参数,每个参数只考虑五个候选值。那么,对于每一组训练/测试集,我们就需要评估5^3=125个不同的模型。由此可见,找到一个合适的参数组合对于算法研究人员来说是多么的重要和令人欣喜。
最后,当我们的模型和参数调整都完成后,为了确保模型能够达到最佳的学习效果,我们需要用初始数据集D重新训练模型。这意味着,之前用于评估的测试集也将被用于训练,以进一步增强模型的性能。这就像我们在高中时期,每次考试结束后,都会认真复习试卷上的题目,即使有些题目是之前没见过的,这样也能让我们更好地掌握知识,从而更加自信地面对接下来的学习。
5、 性能度量
性能度量(performance measure)是评估模型泛化能力的关键指标,用于比较不同模型的优劣。在对比不同模型时,采用不同的性能度量方法可能会导致不同的评判结果。本节将重点介绍分类模型的性能度量,除了5.1之外的内容,都将围绕这一主题展开。
5.1 最常见的性能度量
在回归任务中,也就是预测连续数值的问题中,我们通常采用“均方误差”(mean squared error)作为主要的性能度量标准。许多经典的算法都将MSE作为评价函数,想必大家对此都不陌生。
E ( f ; D ) = 1 m ∑ i = 1 m ( f ( x i ) − y i ) 2 E(f;D)=\frac{1}{m}\sum ^ m_{i=1}(f(x_i)-y_i)^2 E(f;D)=m1i=1∑m(f(xi)−yi)2
在分类任务中,也就是预测离散值的问题中,我们最常用的评价指标是错误率和精度。错误率指的是分类错误的样本数占总样本数的比例,而精度则是分类正确的样本数占总样本数的比例。显然,错误率和精度之间存在互补关系,即错误率与精度之和等于1。
E ( f ; D ) = 1 m ∑ i = 1 m ∥ ( f ( x i ) ≠ y i ) E(f;D)=\frac{1}{m}\sum ^ m_{i=1}\parallel(f(x_i) \neq y_i) E(f;D)=m1i=1∑m∥(f(xi)=yi)
5.2 查准率/查全率/F1
虽然错误率和精度是分类任务中常用的性能度量方式,但它们并不适用于所有场景。例如,在推荐系统中,我们更关注推送的内容是否真正符合用户的兴趣(即查准率),以及我们是否成功推送了所有用户可能感兴趣的内容(即查全率)。因此,对于这类问题,使用查准率和查全率作为评价指标更为合适。在二分类问题中,我们可以通过构建分类结果的混淆矩阵来明确定义查准率和查全率。

查准率P与查全率R分别定义为:
P = T P T P + F P P = \frac{TP}{TP+FP} P=TP+FPTP
R = T P T P + F N R = \frac{TP}{TP+FN} R=TP+FNTP
初次接触时,FN和FP的概念确实容易混淆。按照常规思维,我们可能会将FN误解为“False预测为Negative”,即错误地预测为错误的情况,但这样的理解实际上颠倒了FN和TN的意义。后来,我找到了一张非常详细的图解,它清晰地解释了这些概念。
正如天下没有免费的午餐,查准率和查全率是一对矛盾的度量。例如,如果我们希望推送的内容能够完全吸引用户的兴趣,那么可能只会选择那些我们非常确定的内容进行推送,这样就会遗漏一些用户可能也感兴趣的内容,导致查全率降低。相反,如果我们希望确保所有用户感兴趣的内容都能被推送,那么可能需要推送更多的内容,甚至包括那些不那么确定的内容,这样做虽然提高了查全率,但也会导致查准率下降,因为推送中包含了更多用户不感兴趣的内容。
为了更直观地描述查准率和查全率之间的变化关系,我们引入了“P-R曲线”。这条曲线是根据学习器的预测结果对测试样本进行排序后绘制的。我们首先将最有可能是“正例”的样本放在前面,最不可能是“正例”的样本放在后面。然后,按照这个顺序逐个将样本作为“正例”进行预测,并计算每次预测后的查准率(P值)和查全率(R值)。通过这种方式,我们可以得到一条描述查准率和查全率之间关系的曲线,从而更全面地评估学习器的性能。如下图所示:

那么,如何评估P-R曲线呢?如果学习器A的P-R曲线完全被学习器B的曲线所包围,那么我们可以断定B的性能要优于A。然而,当A和B的曲线出现交叉时,判断性能优劣就变得复杂了。通常,我们会比较两个曲线下的面积,面积较大的学习器性能更优。不过,由于计算曲线下的面积往往比较困难,因此我们引入了“平衡点”(Break-Event Point,简称BEP)的概念。平衡点即查准率与查全率相等时的取值,平衡点越高,说明学习器的性能越好。
在实际应用中,查准率(P)和查全率(R)有时会出现相互矛盾的情况,这就需要我们综合考虑这两个指标。为此,最常用的方法是计算F-Measure,也称为F-Score。F-Measure实际上是P和R的加权调和平均值,通过这一指标,我们可以更全面地评估学习器的性能。F-Measure是P和R的加权调和平均,即:
1 F β = 1 β 2 . ( 1 P + β 2 R ) \frac{1}{F_\beta}=\frac{1}{\beta^2}.(\frac{1}{P}+\frac{\beta^2}{R}) Fβ1=β21.(P1+Rβ2)
特别地,当β=1时,也就是常见的F1度量,是P和R的调和平均,当F1较高时,模型的性能越好。
1 F β = 1 β 2 . ( 1 P + β 2 R ) \frac{1}{F_\beta}=\frac{1}{\beta^2}.(\frac{1}{P}+\frac{\beta^2}{R}) Fβ1=β21.(P1+Rβ2)
F 1 = 2 ∗ P ∗ R P + R = 2 ∗ T P 样本总数 + T P − T N F1=\frac{2*P*R}{P+R}=\frac{2*TP}{样本总数+TP-TN} F1=P+R2∗P∗R=样本总数+TP−TN2∗TP
当我们面对多个二分类混淆矩阵时,例如在多次训练或不同数据集上训练得到的结果,我们需要一种方法来估算全局性能。常用的方法有宏观和微观两种。宏观方法首先计算每个混淆矩阵的P值和R值,然后求得平均P值(macro-P)和平均R值(macro-R),最后基于这些平均值计算Fβ或F1。而微观方法则是先计算出所有混淆矩阵的TP、FP、TN、FN的平均值,然后再基于这些平均值计算P、R,并最终求得Fβ或F1。两种方法从不同的角度综合了多个混淆矩阵的信息,以得到全局的性能评估。
m a c r o − P = 1 n ∑ i = 1 m P i macro-P=\frac{1}{n}\sum ^ m_{i=1}P_i macro−P=n1i=1∑mPi
m a c r o − R = 1 n ∑ i = 1 m R i macro-R=\frac{1}{n}\sum ^ m_{i=1}R_i macro−R=n1i=1∑mRi
m a c r o − F 1 = 2 ∗ m a c r o − P ∗ m a c r o − R m a c r o − P + m a c r o − R macro-F1=\frac{2*macro-P*macro-R}{macro-P + macro-R} macro−F1=macro−P+macro−R2∗macro−P∗macro−R
5.3 ROC与AUC
如前所述,学习器对测试样本的预测结果通常以实值或概率形式给出。当我们设定一个阈值时,预测值大于这个阈值的样本被判断为正例,小于阈值的则判断为负例。因此,这个实值的准确性直接决定了学习器的泛化能力。若我们将这些实值进行排序,排序的质量则反映了学习器的性能水平。ROC曲线正是基于这一思路来评估学习器的泛化性能。与P-R曲线类似,ROC曲线也是按照预测值的排序顺序,逐一将样本视为正例进行预测。但不同之处在于,ROC曲线以“真正例率”(TPR)作为横轴,以“假正例率”(FPR)作为纵轴。ROC曲线更侧重于研究基于测试样本预测值的排序效果,从而评估学习器的性能。
AUC是ROC曲线下的面积
简单分析图像,可以得知:当FN=0时,TN也必须0,反之也成立,我们可以画一个队列,试着使用不同的截断点(即阈值)去分割队列,来分析曲线的形状,(0,0)表示将所有的样本预测为负例,(1,1)则表示将所有的样本预测为正例,(0,1)表示正例全部出现在负例之前的理想情况,(1,0)则表示负例全部出现在正例之前的最差情况。限于篇幅,这里不再论述。
现实中的任务通常都是有限个测试样本,因此只能绘制出近似ROC曲线。绘制方法:首先根据测试样本的评估值对测试样本排序,接着按照以下规则进行绘制。
同样地,进行模型的性能比较时,若一个学习器A的ROC曲线被另一个学习器B的ROC曲线完全包住,则称B的性能优于A。若A和B的曲线发生了交叉,则谁的曲线下的面积大,谁的性能更优。ROC曲线下的面积定义为AUC(Area Uder ROC Curve),不同于P-R的是,这里的AUC是可估算的,即AOC曲线下每一个小矩形的面积之和。易知:AUC越大,证明排序的质量越好,AUC为1时,证明所有正例排在了负例的前面,AUC为0时,所有的负例排在了正例的前面。
6、比较检验
在比较学习器泛化性能的过程中,统计假设检验(hypothesis test)为学习器性能比较提供了重要依据,即若A在某测试集上的性能优于B,那A学习器比B好的把握有多大。 为方便论述,本篇中都是以“错误率”作为性能度量的标准。
6.1 假设检验
“假设”指的是对样本总体的分布或已知分布中某个参数值的一种猜想,例如:假设总体服从泊松分布,或假设正态总体的期望u=u0。回到本篇中,我们可以通过测试获得测试错误率,但直观上测试错误率和泛化错误率相差不会太远,因此可以通过测试错误率来推测泛化错误率的分布,这就是一种假设检验。


7、 偏差与方差
偏差-方差分解是解释学习器泛化性能的重要工具。在学习算法中,偏差指的是预测的期望值与真实值的偏差,方差则是每一次预测值与预测值得期望之间的差均方。实际上,偏差体现了学习器预测的准确度,而方差体现了学习器预测的稳定性。通过对泛化误差的进行分解,可以得到:
期望泛化误差=方差+偏差
偏差刻画学习器的拟合能力
方差体现学习器的稳定性
易知:方差和偏差具有矛盾性,这就是常说的偏差-方差窘境(bias-variance dilamma),随着训练程度的提升,期望预测值与真实值之间的差异越来越小,即偏差越来越小,但是另一方面,随着训练程度加大,学习算法对数据集的波动越来越敏感,方差值越来越大。换句话说:在欠拟合时,偏差主导泛化误差,而训练到一定程度后,偏差越来越小,方差主导了泛化误差。因此训练也不要贪杯,适度辄止。
相关文章:

【机器学习-05】模型的评估与选择
在前面【机器学习-01】机器学习基本概念与建模流程的文章中我们已经知道了机器学习的一些基本概念和模型构建的流程,本章我们将介绍模型训练出来后如何对模型进行评估和选择等 1、 误差与过拟合 学习器对样本的实际预测结果与真实值之间的差异,我们称之…...
【11】工程化
一、为什么需要模块化 当前端工程到达一定规模后,就会出现下面的问题: 全局变量污染 依赖混乱 上面的问题,共同导致了代码文件难以细分 模块化就是为了解决上面两个问题出现的 模块化出现后,我们就可以把臃肿的代码细分到各个小文件中,便于后期维护管理 前端模块化标准…...

Python中requests、aiohttp、httpx性能对比
在Python中,有许多用于发送HTTP请求的库,其中最受欢迎的是requests、aiohttp和httpx。这三个库的性能和功能各不相同,因此在选择使用哪个库时,需要考虑到自己的需求和应用场景。 首先,让我们来了解一下这三个库的基本…...
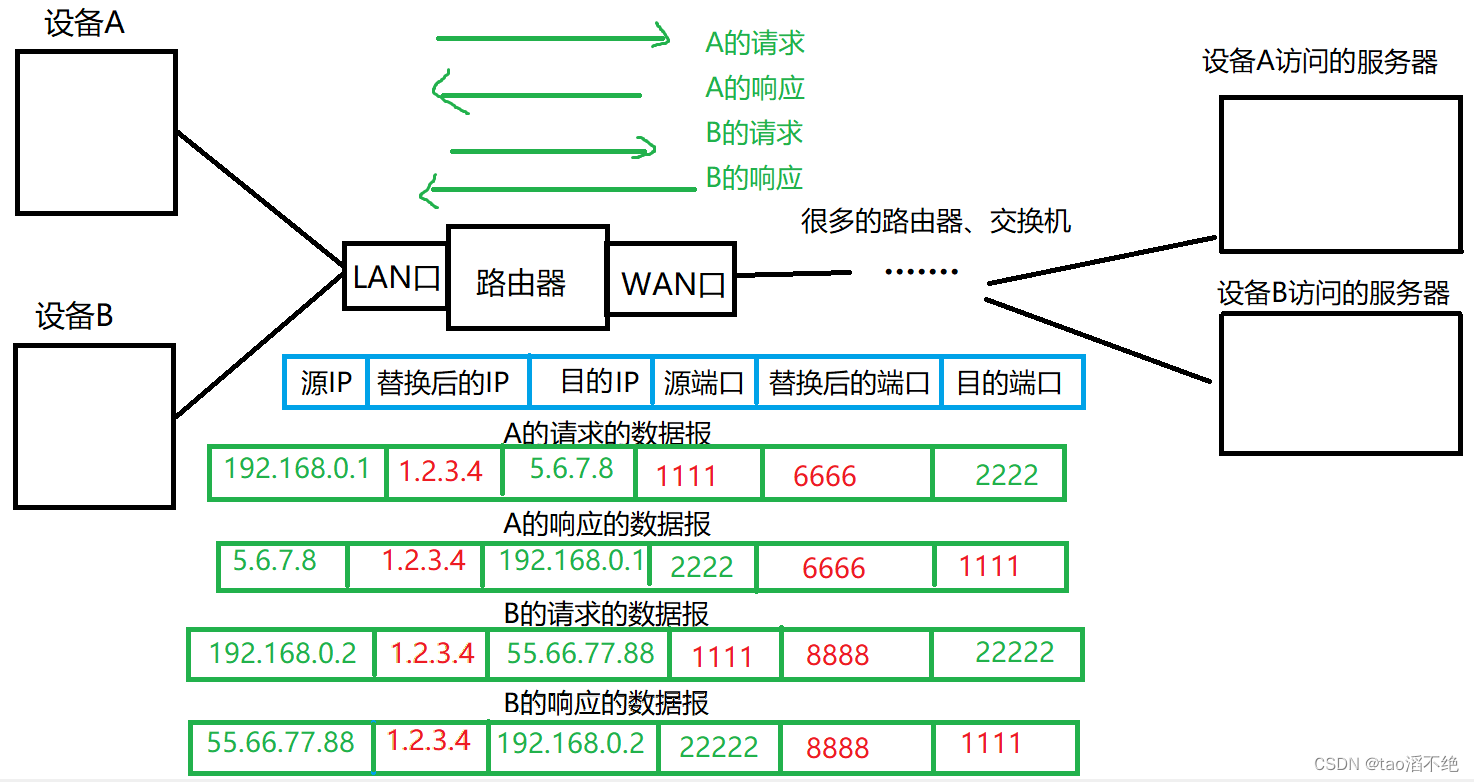
网络原理(5)——IP协议(网络层)
目录 一、IP协议报头介绍 1、4位版本 2、4位首部长度 3、8位服务器类型 4、16位总长度 5、16位标识位 6、3位标志位 7、13位偏移量 8、8位生存空间 9、8位协议 10、16位首部检验和 11、32位源IP地址 12、32位目的IP地址 二、IP协议如何管理地址? 1、动…...

GE IS200AEPAH1BKE IS215WEPAH2BB是两种不同的压力测量模块
GE IS200AEPAH1BKE和IS215WEPAH2BB是两种不同的压力测量模块,它们都属于GE(通用电气)公司的产品。 具体来说,以下是这两种模块的一些特点和应用: IS200AEPAH1BKE:这款模块适用于需要高性价比的压力测量应用…...

Rust 与 C++ ,孰优孰劣?
Rust 与 C 是两种高级系统级编程语言,它们都在追求性能、控制底层硬件细节的同时强调安全性。以下是两者的详细对比: 目标与理念 Rust:由 Mozilla 主导开发,目标是构建一种既快速又安全的系统级编程语言,特别是解决 C…...

MySQL、Oracle的时间类型字段自动更新:insert插入、update更新时,自动更新时间戳
1.MySQL 支持的字段类型:DATETIME、TIMESTAMP drop table if exists test_time_auto_update; create table test_time_auto_update (id bigint auto_increment primary key comment 自增id,name varchar(8) …...
Testng框架集成新业务
总体框架设计见我另一篇博客:httpclienttestng接口自动化整体框架设计 <block:表示测试用例块> block后面是 测试用例的名称 ||接口名,该接口名在URL.txt里维护接口 ||get\post:表示请求的方法 get_1\2\3\4:代表加密 get: …...

springboot 单元测试
Spring Boot 单元测试是确保代码质量的重要部分,它允许我们在不实际启动整个应用的情况下测试我们的代码。在Spring Boot中,我们通常使用Spring Test模块和JUnit测试框架来编写单元测试。以下是一个简单的Spring Boot单元测试的详细代码介绍:…...

LeetCode---126双周赛
题目列表 3079. 求出加密整数的和 3080. 执行操作标记数组中的元素 3081. 替换字符串中的问号使分数最小 3082. 求出所有子序列的能量和 一、求出加密整数的和 按照题目要求,直接模拟即可,代码如下 class Solution { public:int sumOfEncryptedInt…...

[python] ETL 工作流程 Prefect
Prefect 是一个用于构建、调度和监控数据流程的 Python 库。它提供了一种简单而强大的方式来管理 ETL(Extract, Transform, Load)工作流程。下面是一个简单的示例,演示了如何使用 Prefect 来创建和运行一个简单的任务: 首先&…...
html第一次作业
常用标签 0, 骨架(!tap) <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><t…...
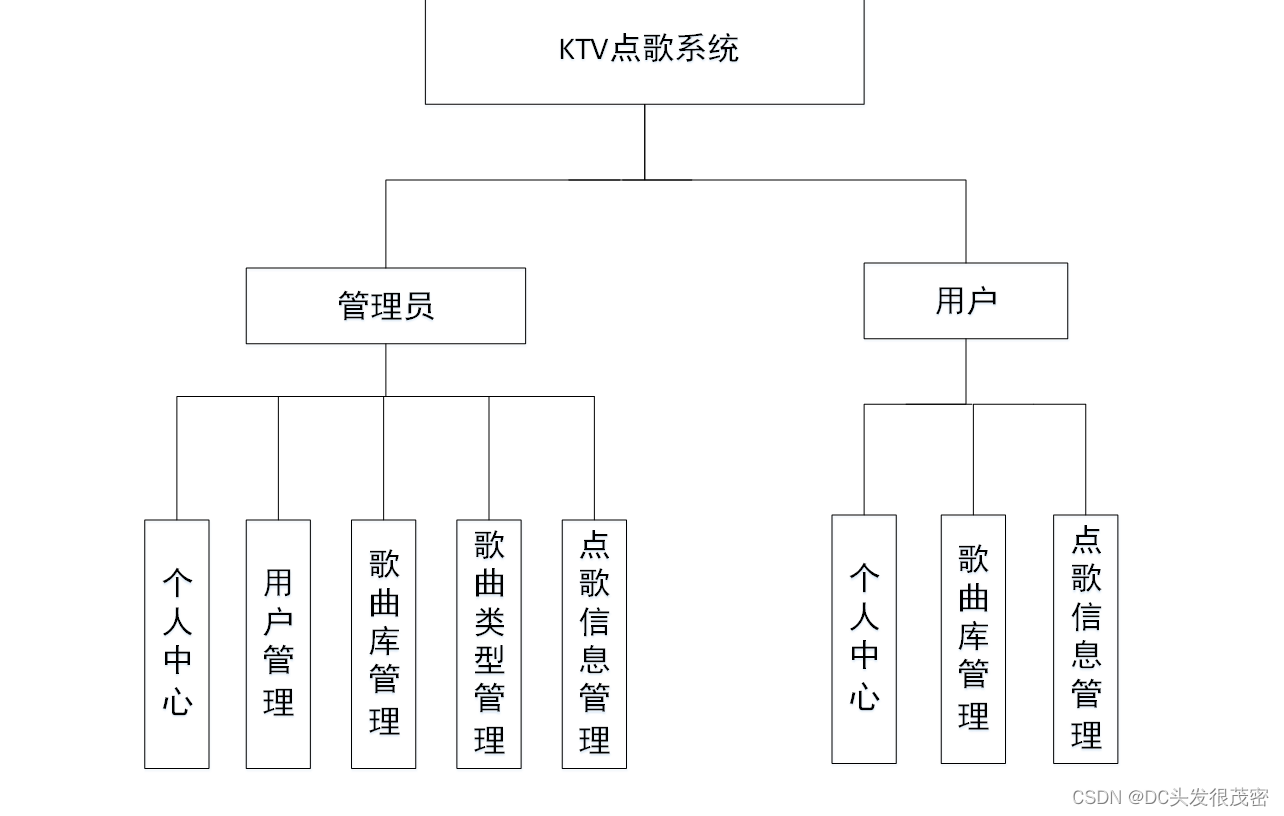
基于java实现的KTV点歌系统
开发语言:Java 框架:ssm 技术:JSP JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件:eclipse/myeclip…...

GPT+向量数据库+Function calling=垂直领域小助手
引言 将 GPT、向量数据库和 Function calling 结合起来,可以构建一个垂直领域小助手。例如,我们可以使用 GPT 来处理自然语言任务,使用向量数据库来存储和管理领域相关的数据,使用 Function calling 来实现领域相关的推理和计算规…...
DeepSeek-coder 微调训练记录
简介 微调过程不再细说, 参考link进行即可. 主要是数据集. 1.3b模型微调训练占用资源信息 top信息 评估 根据DeepSeek-coder的Evaluation试进行对微调后的模型进行评估. 其中的评估库主要是evol-teacher和human-eval. 新建一个eval_ins.sh文件, 填入以下内容 LANG"…...
)
【Android】【Bluetooth Stack】蓝牙音乐协议分析之音频控制与信息加载(超详细)
1. 精讲蓝牙协议栈(Bluetooth Stack):SPP/A2DP/AVRCP/HFP/PBAP/IAP2/HID/MAP/OPP/PAN/GATTC/GATTS/HOGP等协议理论 2. 欢迎大家关注和订阅,【蓝牙协议栈】和【Android Bluetooth Stack】专栏会持续更新中.....敬请期待! 目录 1. 音乐信息加载 1.1 歌曲信息 1.1.1 key_c…...
ChatGPT无法登录,提示我们检测到可疑的登录行为?如何解决?
OnlyFans 订阅教程移步:【保姆级】2024年最新Onlyfans订阅教程 Midjourney 订阅教程移步: 【一看就会】五分钟完成MidJourney订阅 GPT-4.0 升级教程移步:五分钟开通GPT4.0 如果你需要使用Wildcard开通GPT4、Midjourney或是Onlyfans的话&am…...

程序员表白
啥?!你说程序员老实,认真工作,根本不会什么表白!那你就错了!(除了我) 那今天我们就来讲一下这几个代码!赶紧复制下来,这些代码肯定有你有用的时候! 1.Python爱心代码 im…...

CSS的使用与方法
什么是CSS CSS是层叠样式表。它是一种用于描述网页或者文档外观和样式的标记语言。 层级样式表:就是给HTML标签加样式的。 如果说HTML是个游戏英雄 、那么CSS就是游戏皮肤。 【一】注释语法 /* 注释 */ 【二】CSS的语法结构 选择符 {样式属性: 样式属性值;样…...
离线安装mongoDB集群)
(保姆级)离线安装mongoDB集群
Docker搭建MongoDB集群 副本集模式(Replica Set) 是一种互为主从的关系, Replica Set 将数据复制多份保存,不同服务器保存同一份数据,在出现故障时自动切换,实现故障转移。 此集群拥有一个主节点和多个从…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
