算法公式汇总
文章目录
- 三角函数
- 定义式
- 诱导公式
- 平方关系
- 两角和与差的三角函数
- 积化和差公式
- 和差化积公式
- 倍角公式
- 半角公式
- 万能公式
- 其他公式
- 反三角函数恒等式
- 三角函数
- 定义式
三角函数
定义式
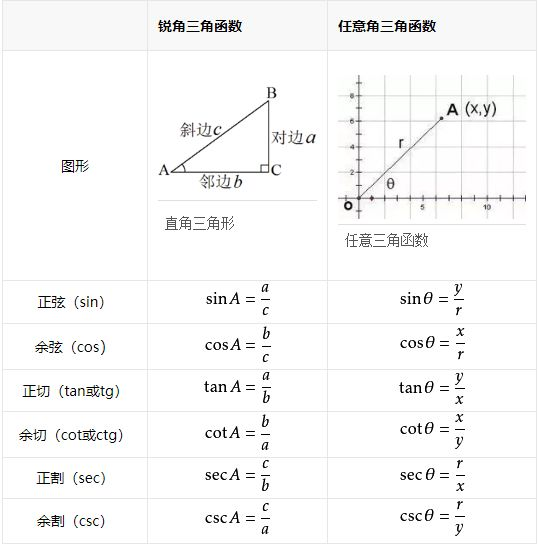
余切: c o t A = 1 t a n A \text { 余切:} \ cotA = \frac{1}{tanA} 余切: cotA=tanA1
正切: s e c A = 1 c o s A \text { 正切:} \ secA = \frac{1}{cosA} 正切: secA=cosA1
余割: c s c A = 1 s i n A \text { 余割:} \ cscA = \frac{1}{sinA} 余割: cscA=sinA1
反正切: a r c t a n ( t a n X ) = t a n ( a r c t a n X ) = X \text { 反正切:} \ arctan(tanX) = tan(arctanX) = X 反正切: arctan(tanX)=tan(arctanX)=X
诱导公式
- sin ( − α ) = − sin α
- cos ( − α ) = cos α
- sin ( π 2 − α ) = cos α
- cos ( π 2 − α ) = sin α
- sin ( π 2 + α ) = cos α
- cos ( π 2 + α ) = − sin α
- sin ( π − α ) = sin α
- cos ( π − α ) = − cos α
- sin ( π + α ) = − sin α
- cos ( π + α ) = − cos α
平方关系
1 + t a n 2 α = s e c 2 α 1 + tan^2α = sec^2α 1+tan2α=sec2α
1 + c o t 2 α = c s c 2 α 1 + cot^2α = csc^2α 1+cot2α=csc2α
s i n 2 α + c o s 2 α = 1 sin^2α + cos^2α = 1 sin2α+cos2α=1
两角和与差的三角函数
s i n ( α + β ) = s i n α c o s β + c o s α s i n β sin ( α + β ) = sin α cos β + cos α sin β sin(α+β)=sinαcosβ+cosαsinβ
c o s ( α + β ) = c o s α c o s β − s i n α s i n β cos ( α + β ) = cos α cos β − sin α sin β cos(α+β)=cosαcosβ−sinαsinβ
s i n ( α − β ) = s i n α c o s β − c o s α s i n β sin ( α − β ) = sin α cos β − cos α sin β sin(α−β)=sinαcosβ−cosαsinβ
c o s ( α − β ) = c o s α c o s β + s i n α s i n β cos ( α − β ) = cos α cos β + sin α sin β cos(α−β)=cosαcosβ+sinαsinβ
t a n ( α + β ) = t a n α + t a n β 1 − t a n α t a n β tan ( α + β ) = \frac{ tan α + tan β}{1 - tan α tan β} tan(α+β)=1−tanαtanβtanα+tanβ
t a n ( α − β ) = t a n α − t a n β 1 + t a n α t a n β tan ( α − β ) = \frac{ tan α - tan β}{1 + tan α tan β} tan(α−β)=1+tanαtanβtanα−tanβ
积化和差公式
c o s α c o s β = 1 2 [ c o s ( α + β ) + c o s ( α − β ) ] cos α cos β = \frac{1}{2} [ cos ( α + β ) + c o s ( α − β ) ] cosαcosβ=21[cos(α+β)+cos(α−β)]
c o s α s i n β = 1 2 [ s i n ( α + β ) − s i n ( α − β ) ] cos α sin β = \frac{1}{2} [ sin ( α + β ) - sin ( α − β ) ] cosαsinβ=21[sin(α+β)−sin(α−β)]
s i n α c o s β = 1 2 [ s i n ( α + β ) + s i n ( α − β ) ] sin α cos β = \frac{1}{2} [ sin ( α + β ) + sin ( α − β ) ] sinαcosβ=21[sin(α+β)+sin(α−β)]
s i n α s i n β = − 1 2 [ c o s ( α + β ) + c o s ( α − β ) ] sin α sin β = -\frac{1}{2} [ cos ( α + β ) + c o s ( α − β ) ] sinαsinβ=−21[cos(α+β)+cos(α−β)]
和差化积公式
s i n α + s i n β = 2 s i n α + β 2 c o s α − β 2 sin α + sin β = 2 sin \frac{α + β}{2} cos \frac{α - β}{2} sinα+sinβ=2sin2α+βcos2α−β
s i n α − s i n β = 2 c o s α + β 2 s i n α − β 2 sin α - sin β = 2 cos \frac{α + β}{2} sin \frac{α - β}{2} sinα−sinβ=2cos2α+βsin2α−β
c o s α + c o s β = 2 c o s α + β 2 c o s α − β 2 cos α + cos β = 2 cos \frac{α + β}{2} cos \frac{α - β}{2} cosα+cosβ=2cos2α+βcos2α−β
c o s α − c o s β = − 2 s i n α + β 2 s i n α − β 2 cos α - cos β = -2 sin \frac{α + β}{2} sin \frac{α - β}{2} cosα−cosβ=−2sin2α+βsin2α−β
倍角公式
s i n 2 α = 2 s i n α c o s α sin 2 α = 2 sin α cos α sin2α=2sinαcosα
c o s 2 α = c o s 2 α − s i n 2 α = 1 − 2 s i n 2 α = 2 c o s 2 α − 1 cos 2 α = cos ^2 α − sin ^2 α = 1 − 2 sin ^2 α = 2 cos ^2 α − 1 cos2α=cos2α−sin2α=1−2sin2α=2cos2α−1
s i n 3 α = − 4 s i n 3 α + 3 s i n α sin 3 α = − 4 sin ^3 α + 3 sin α sin3α=−4sin3α+3sinα
c o s 3 α = 4 c o s 3 α − 3 c o s α cos 3 α = 4 cos ^3 α − 3 cos α cos3α=4cos3α−3cosα
s i n 2 α = 1 − c o s 2 α 2 sin ^2 α = \frac{1 − cos 2 α}{2} sin2α=21−cos2α
c o s 2 α = 1 + c o s 2 α 2 cos ^2 α = \frac{1 + cos 2 α}{2} cos2α=21+cos2α
t a n 2 α = 2 t a n α 1 − t a n 2 α tan 2 α = \frac{2 tan α}{1 − tan ^2 α } tan2α=1−tan2α2tanα
c o t 2 α = c o t 2 α − 1 2 c o t α cot 2 α = \frac{cot ^2 α − 1}{2 cot α} cot2α=2cotαcot2α−1
半角公式
s i n 2 α 2 = 1 − c o s α 2 sin ^2 \frac{α}{2} = \frac{1 − cos α}{2} sin22α=21−cosα
c o s 2 α 2 = 1 + c o s α 2 cos ^2 \frac{α}{2} = \frac{1 + cos α}{2} cos22α=21+cosα
s i n α 2 = ± 1 − c o s α 2 sin \frac{α}{2} = ±\sqrt{\frac{1 - cos α}{2}} sin2α=±21−cosα
c o s α 2 = ± 1 + c o s α 2 cos \frac{α}{2} = ±\sqrt{\frac{1 + cos α}{2}} cos2α=±21+cosα
t a n α 2 = 1 − c o s α s i n α = s i n α 1 + c o s α = ± 1 − c o s α 1 + c o s α tan \frac{α}{2} = \frac{1 - cos α}{sin α} = \frac{sin α}{1 + cos α } = ±\sqrt{\frac{1 - cos α}{1 + cos α}} tan2α=sinα1−cosα=1+cosαsinα=±1+cosα1−cosα
c o t α 2 = s i n α 1 − c o s α = 1 + c o s α s i n α = ± 1 + c o s α 1 − c o s α cot \frac{α}{2} = \frac{sin α}{1 - cos α} = \frac{1 + cos α }{sin α } = ±\sqrt{\frac{1 + cos α}{1 - cos α}} cot2α=1−cosαsinα=sinα1+cosα=±1−cosα1+cosα
万能公式
s i n α = 2 t a n α 2 1 + t a n 2 α 2 sin α = \frac{2tan \frac{α}{2}}{1 + tan ^2 \frac{α}{2}} sinα=1+tan22α2tan2α
c o s α = 1 − t a n 2 α 2 1 + t a n 2 α 2 cos α = \frac{1 - tan ^2 \frac{α}{2}}{1 + tan ^2 \frac{α}{2}} cosα=1+tan22α1−tan22α
其他公式
1 + s i n α = ( s i n α 2 + c o s α 2 ) 2 1 + sin α = ( sin \frac{α}{2} + cos \frac{α}{2}) ^2 1+sinα=(sin2α+cos2α)2
1 − s i n α = ( s i n α 2 − c o s α 2 ) 2 1 - sin α = ( sin \frac{α}{2} - cos \frac{α}{2}) ^2 1−sinα=(sin2α−cos2α)2
反三角函数恒等式
a r c s i n x + a r c c o s x = π 2 arcsin x + arccos x = \frac{π}{2} arcsinx+arccosx=2π
a r c t a n x + a r c c o t x = π 2 arctan x + arccot x = \frac{π}{2} arctanx+arccotx=2π
s i n ( a r c c o s x ) = 1 − x 2 sin ( arccos x ) = \sqrt{1 − x ^2} sin(arccosx)=1−x2
c o s ( a r c s i n x ) = 1 − x 2 cos ( arcsin x ) = \sqrt{1 − x ^2} cos(arcsinx)=1−x2
s i n ( a r c s i n x ) = x sin ( arcsin x ) = x sin(arcsinx)=x
a r c s i n ( s i n x ) = x arcsin ( sin x ) = x arcsin(sinx)=x
c o s ( a r c c o s x ) = x cos ( arccos x ) = x cos(arccosx)=x
a r c c o s ( c o s x ) = x arccos ( cos x ) = x arccos(cosx)=x
a r c c o s ( − x ) = π − a r c c o s x arccos ( − x ) = π − arccos x arccos(−x)=π−arccosx
三角函数
定义式
相关文章:

算法公式汇总
文章目录 三角函数定义式诱导公式平方关系两角和与差的三角函数积化和差公式和差化积公式倍角公式半角公式万能公式其他公式反三角函数恒等式 三角函数定义式 三角函数 定义式 余切: c o t A 1 t a n A \text { 余切:} \ cotA \frac{1}{tanA} 余切&a…...

c语言管理课程信息系统
定制魏:QTWZPW,获取更多源码等 目录 题目要求 数据结构 函数设计 结构设计 管理员功能: 学生功能: 效果展示 总结 主函数代码 题目要求 管理课程信息系统,允许管理员和学生执行不同的操作。管理员可以添加、浏览、查询、删除、修改和排序课程信息。学生可以…...

大模型在天体物理学研究中的辅助作用与案例分析
大模型在天体物理学研究中的辅助作用与案例分析 1. 背景介绍 天体物理学是研究宇宙中各种天体的物理性质和运动规律的科学。随着观测技术的进步,天体物理学家们获得了大量的数据,这些数据往往具有高维度、非线性、非平稳等特点,给传统的数据…...
洛谷_P1873 [COCI 2011/2012 #5] EKO / 砍树_python写法
P1873 [COCI 2011/2012 #5] EKO / 砍树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) n, m map(int,input().split())data list(map(int,input().split())) h 0 def check(mid):h 0for i in data:if i>mid:h (i-mid)if h < m:return Trueelse:return Falsel 0 r …...

Android_NDK调试
第一步: 链接log动态库 在Android.mk文件中添加 LOCAL_LDLIBS -llog 注意:一定要在 include $(BUILD_SHARED_LIBRARY) 之上添加,因为当执行到这句话的时候就表示所有的lib动态库已经加载完毕了,所以当你在这句代码之后再添加…...
)
全量知识系统 概要设计(SmartChat回复)
以下是根据我给出的 系统概要 “提要和纪要”,SmartChat给出的概要设计。我给出的“提要和纪要”可参考链接: https://blog.csdn.net/ChuanfangChen/article/details/136861822 -------------------------------- 概要设计文档 1. 简介 全量知识系统…...
一、SpringBoot基础搭建
本教程主要给初学SpringBoot的开发者,通过idea搭建单体服务提供手把手教学例程,主要目的在于理解环境的搭建,以及maven模块之间的整合与调用 源码:jun/learn-springboot 以商城项目为搭建例子,首先计划建1个父模块&…...

some/ip CAN CANFD
关于SOME/IP的理解 在CAN总线的车载网络中,通信过程是面向信号的 当ECU的信号的值发生了改变,或者发送周期到了,就会发送消息,而不考虑接收者是否需要,这样就会造成总线上出现不必要的信息,占用了带宽 …...

HTTP Header Fields
HTTP(超文本传输协议)中包含多种类型的头部字段(Header Fields),以下是常见的HTTP头部字段及其作用: ### 通用头字段(General Header Fields) - **Cache-Control**: 控制缓存行为&a…...

基于FPGA的FFT图像滤波设计
1.FFT滤波算法介绍 FFT滤波就是通过傅里叶运算将图像转换到频域空间,然后在频域中对图像进行处理,最后将处理后的图像通过傅里叶逆运算将图像转会到时域空间。 在频域空间中,我们能够更好的对图像的噪声进行分析,然后找出相关规律…...
WPF 立体Border
WPF 立体Border ,用来划分各个功能区块 在资源文件中,添加如下样式代码: <Style x:Key"BaseBorder" TargetType"Border"><Setter Property"Background" Value"White" /><Setter Prop…...

java.lang.ClassNotFoundException: kotlin.jvm.internal.Intrinsics
今天在使用springBoot连接influxdb报错 java.lang.ClassNotFoundException: kotlin.jvm.internal.Intrinsics 详细报错如下,提出我们缺少一个依赖 原因是由于创建influxdb客户端缺少Kotlin运行时库 解决办法就是 1.显示的添加okhttp的依赖 <dependency>…...
代码随想录(day8)——字符串
Leetcode.344 反转字符串: 344. 反转字符串 - 力扣(LeetCode) 原理过于简单,没什么好说的,直接给出代码: class Solution { public:void reverseString(vector<char>& s) {int end s.size()-1…...

JavaScript 权威指南第七版(GPT 重译)(二)
第四章:表达式和运算符 本章记录了 JavaScript 表达式以及构建许多这些表达式的运算符。表达式 是 JavaScript 的短语,可以 评估 以产生一个值。在程序中直接嵌入的常量是一种非常简单的表达式。变量名也是一个简单表达式,它评估为分配给该变…...
【python_往企业微信群中发送文件】
python_往企业微信群中发送文件 这个是用企业微信群机器人的功能,没有用到后台应用。群机器人 #-*- coding:utf-8-* import requests#类型:voice,file file_type"file" file_path"D:\desktop\不过.jpg" webhookkey"xxxx"#…...
)
华为校招机试 - 循环依赖(20240320)
题目描述 给定一组元素,及其依赖关系,一个元素可以依赖于多个元素(不包括自己,被依赖元素不会重复),一个元素也可被多个元素依赖。 假定总是存在唯一的循环依赖,请输出该循环依赖。 输入描述 第一行是个正整数 N (1 < N < 100),表示依赖关系的个数。 下面每…...

基于Spring Boot技术的幼儿园管理系统
摘 要 随着信息时代的来临,过去的传统管理方式缺点逐渐暴露,对过去的传统管理方式的缺点进行分析,采取计算机方式构建幼儿园管理系统。本文通过课题背景、课题目的及意义相关技术,提出了一种活动信息、课程信息、菜谱信息、通知公…...

查找众数及中位数 - 华为OD统一考试(C卷)
OD统一考试(C卷) 分值: 100分 题解: Java / Python / C++ 题目描述 众数是指一组数据中出现次数量多的那个数,众数可以是多个。 中位数只是指把一组数据从小到大排列,最中间的那个数,如果这组数据的个数是奇数,那最中间那个就是中位数,如果这组数据的个数为偶数,那…...

bash命令执行.sh文件 windows python环境
报错: bash : 无法将“bash”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。请检查名称的拼写,如果包括路径,请确保路径正确,然后再试一次。 所在位置 行:1 字符: 1 ’ bash fetch_data.sh ‘ ~~~~ CategoryInfo : Object…...

refreactive vue3
ref 可以定义:基本类型、对象类型的响应式数据 reactive 只能定义:对象类型的响应式数据 <template><div class"person"><h2>Name: {{ name }}</h2><h2>Age: {{ age }}</h2><h2>Tel: {{ tel }}</h2><button cl…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
