【No.13】蓝桥杯二分查找|整数二分|实数二分|跳石头|M次方根|分巧克力(C++)
二分查找算法
知识点
- 二分查找原理讲解
- 在单调递增序列
a中查找x或x的后继 - 在单调递增序列
a中查找x或x的前驱
二分查找算法讲解
枚举查找即顺序查找,
实现原理是逐个比较数组 a[0:n-1] 中的元素,直到找到元素 x 或搜索整个数组后确定 x 不在其中。最坏情况下需要比较 N 次,时间复杂度是 O(n),属于线性阶算法。
而二分查找是一种折半查找方法。
该方法将 N 个元素分成大致相等的两部分,选取中间元素与查找的元素进行比较。
- 如果相等,则查找成功;
- 如果查找元素小于中间元素,则在左半区继续查找;
- 如果查找元素大于中间元素,则在右半区继续查找。
每次都将范围缩小至原来的一半,因此时间复杂度是 O ( log 2 n ) O(\log_{2}n) O(log2n)。
需要注意的是,二分查找的前提是数组有序,一般是从小到大排列。
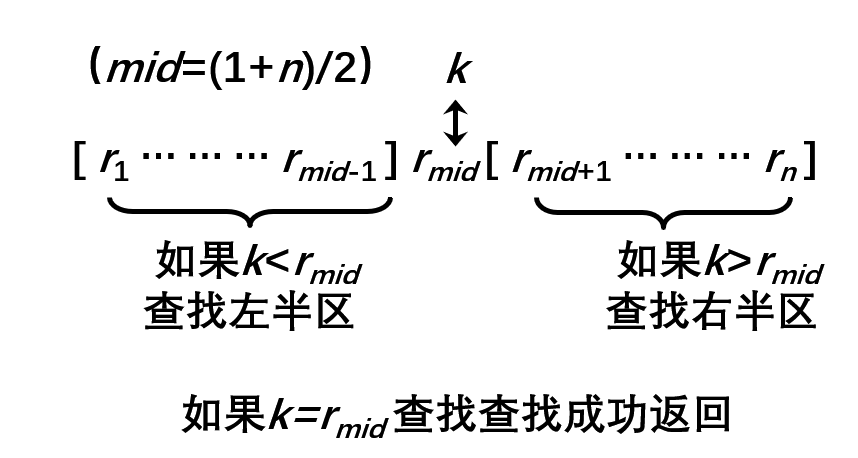
折半查找的基本思想:
在有序表中(low, high, low<=high),取中间记录即a[(high+low)/2]作为比较对象。 - 若给定值与中间记录的关键码相等,则查找成功。
- 若给定值小于中间记录的关键码,则在中间记录的左半区继续查找。
- 若给定值大于中间记录的关键码,则在中间记录的右半区继续查找。
不断重复上述过程,直到查找成功,或所查找的区域无记录,查找失败。
二分查找的特征:
- 答案具有单调性。
- 二分答案的问题往往有固定的问法,例如:令最大值最小(最小值最大),求满足条件的最大(小)值等。
折半查找一般过程:
Step 1:假设存在一个有序数组:
下标[ 0 1 2 3 4 5 6 7 8 9 10 11 12 ]
数据[ 7 14 18 21 23 29 31 35 38 42 46 49 52 ]↑ ↑low=0 high=12mid=(low+high)/2mid=(0+12)/2mid=6[mid]=31 > 14,所以选择左半部分操作:此时令low不变,high=mid-1=5Step 2:下标[ 0 1 2 3 4 5 6 7 8 9 10 11 12 ]
数据[ 7 14 18 21 23 29 31 35 38 42 46 49 52 ]↑ ↑low=0 high=5mid=(low+high)/2mid=(0+6)/2mid=3[mid]=21 > 14,所以选择左半部分操作:此时令low不变,high=mid-1=2Step 3:下标[ 0 1 2 3 4 5 6 7 8 9 10 11 12 ]
数据[ 7 14 18 21 23 29 31 35 38 42 46 49 52 ]↑ ↑low=0 high=2mid=(low+high)/2mid=(0+2)/2mid=1[mid]=14 = 14 找到答案操作:返回下标
整数二分法常用算法模板
// 在单调递增序列a中查找>=x的数中最小的一个(即x或x的后继)
while (low < high)
{int mid = (low + high) / 2;if (a[mid] >= x)high = mid;elselow = mid + 1;
}// 在单调递增序列a中查找<=x的数中最大的一个(即x或x的前驱)
while (low < high)
{int mid = (low + high + 1) / 2; //向右+1个,以便于判断区间的时候落到右侧// int mid = left + (right - left) / 2;if (a[mid] <= x)low = mid;elsehigh = mid - 1;
}
此处我们先分整数的二分查找法的常用模版,关于实数的部分,我们后面再讲。
为什么采用这一套代码的而不是采用查找等于的 X
是因为这样的适用范围更广,当有 X 时这套代码就返回 X 的位置。如果没有 X,就返回 <=x 的数中最大的一个或者 >=x 的数中最小的一个。
跳石头
【题目描述】
“跳石头"比赛在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有n块岩石(不含起点和终点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达终点。
为了提高比赛难度,组委会计划移走些岩石,使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走m块岩石(不能移走起点和终点的岩石)
【输入描述】
输入文件第一行包含三个整数L,N,M,分别表示起点到终点的距离,起点和终点之间的岩石数,以及组委会至多移走的岩石数。
接下来 N行,每行一个整数,第 i行的整数 Di(0<Di<L)表示第 i 块岩石与起点的距离。这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同一个位置。
其中,0≤M≤N≤5x104,1≤L≤109
【输出描述】
输出只包含一个整数,即最短跳跃距离的最大值。
题目解析
二分法套路题:最小值最大化,最大值最小化
在n块岩石中移走m个石头,有很多种移动方法
在第i种移动方法中,剩下的石头之间的距离,有一个最小距离ai.
在所有移动方法的最小距离ai中,问最大的ai是多少
在所有可能的最小值中,找最大的那个,就是最小值最大化
在单调递增的序列中,找到满足某个条件的最大的那个值
- 暴力法:找所有的组合,在n块岩石中选m个石头的组合,情况太多,超时
- 二分思路:不找搬走石头的组合,而是给出一个距离d,检查能不能搬走m块石头而得到最短距离d。把所有的d都试一遍,肯定能找到一个最短的d,用二分法找这个d
最短距离ai,最小可以取到0,最大可以取到L,不管用什么方法,ai一定是这个区间上的一个数
这个区间是一个递增的,有序的,
二分这个区间,找到一个ai,检查这个ai是不是符合题意:是不是能通过n块岩石中移走m块岩石能构造出,最短距离是ai的这么一种情况
如何判断能否通过n块石头中一走m块石头来实现
比如说现在要找的ai是3,有5块石头,它们之间的距离是5,3,4,2,显然5,3,4满足条件,但是2不满足,所以要移走第四块石头,变成5,3,6,可以通过这样的方法来判断是否要移走某块石头
满足了3以后,因为要找最大的,所以解下来判断4,这一组石头里的3就不符合了,移走第二块石头,变成8,6,这样就需要移走两块石头
如果m=2的话,就满足条件,如果m=1就不满足
所以m=1的话,ai就只能是3,m=2的话,可以是4
- 如果是用暴力法去找的话,就是从1开始一直枚举到L
- 1~L是一个有序的枚举,所以可以通过二分去做
1~L。找mid,看这个mid能不能通过移走m块来实现,可以的话,就在右边的区间继续去找,不能移走的话,就从左区间开始找
代码
#include <cstdio>
int len, n, m;
int stone[50005];
bool check(int d) //检查距离d是否合适
{int num = 0; //num记录搬走石头的数量int pos = 0; //当前站立的石头for (int i = 1; i <= n; i ++){if (stone[i]-pos < d)num++; //第i块石头可以搬走elsepos = stone[i]; //第i块石头不能搬走}if (num <= m)return true; //要移动的石头比m少,满足条件elsereturn false; //要移动的石头比m多,不满足条件
}int main()
{scanf("%d%d%d", &len, &n, &m);for (int i = 1; i <= n; i ++){scanf("%d", &stone[i]);}int L = 0, R = len, mid;while (L < R){mid = (L + R + 1) / 2;//查找满足条件的最大的那个值,所以向右贪心if (check(mid)){L = mid; //满足条件,说明mid小了,调大一点}elseR = mid - 1; //不满足条件,说明mid大了,调小一点}printf ("%d\n", L);return 0;
}
M 次方根
题目描述:
小 A 最近在学高等数学,他发现了一道题,求三次根号下27。现在已知,小 A 开始计算,1 的三次方得1,2 的三次方得8,3 的三次方得27,然后他很高兴的填上了3。
接着他要求5次根号下164。然后他开始1 的三次方得1,2 的三次方得8,3 的三次方得27…
直到他算到了秃头,也没有找到答案。
这时一旁的小 B 看不下去了,说这题答案又不是个整数。小 A 震惊,原来如此。作为程序高手的小 A,打算设计一个程序用于求解M次根下N的值。
但是由于要考虑精度范围,答案必须要保留7位小数,连三次根号下27都要掰手指的小 A 又怎么会设计呢。请你帮小 A 设计一个程序用于求解 M 次根号N。
数据范围:
1≤N≤1e5
1≤M≤100
M < N
要求输入:
输入描述:
第一行输入整数 N 和 M,数据间用空格隔开。
要求输出:
输出描述:
输出一个整数,并保留 7 位小数。
样例:
输入样例:
27 3
输出样例:
3.000000
运行限制:
最大运行时间:1s
最大运行内存: 256M
注意:
1. 请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
2. 不要调用依赖于编译环境或操作系统的特殊函数。
3. 所有依赖的函数必须明确地在源文件中。
4. 不能通过工程设置而省略常用头文件。
题目分析
根据前面的知识,我们要找到一个具有单调性的数列,去二分。这个题的关键是我们要去二分什么,这里可以二分的是 a^M 中的 a,所以我们要先想办法设计出用于处理实数二分的代码。
这里给大家两个模板,都可以大家选择一个使用即可:
//模版一:实数域二分,设置eps法//令 eps 为小于题目精度一个数即可。比如题目说保留4位小数,0.0001 这种的。那么 eps 就可以设置为五位小数的任意一个数 0.00001- 0.00009 等等都可以。//一般为了保证精度我们选取精度/100 的那个小数,即设置 eps= 0.0001/100 =1e-6while (l + eps < r) //l加上这个精度<r,就继续二分
//如果不小于r,就说明l-r<eps,代表这两个数之间的精度差距不会超过0.0001,代表找到这个值了
{double mid = (l + r) / 2;if (pd(mid))r = mid;elsel = mid;
}//模版二:实数域二分,规定循环次数法
//通过循环一定次数达到精度要求,这个一般 log_2 N < 精度即可。N 为循环次数,在不超过时间复杂度的情况下,可以选择给 N 乘一个系数使得精度更高。
//为什么循环100次一定可以,二分是每次除以2,除100次2,也就是做100次log_2n,1024是10次。10^6约20次,10^9约30次,所以100次一定可以满足for (int i = 0; i < 100; i++)
{double mid = (l + r) / 2;if (pd(mid))r = mid;elsel = mid;
}
模板讲完了,然后我们就要考虑判定条件了,怎样判定是否存在满足大于平均值的区间。当然这个题你可以使用语言中自带开方软件,但是我们还是联系一下实数的二分代码。
关于判定条件,我们应该设计一个代码用于比较 a^m 和 N 的大小关系。
在我们代码中:
if (pd(mid))r = mid;
elsel = mid;
pd 成功的情况,一定是 pd 的mid 符合条件,且小于 mid 的一定符合条件。因此我们要在大于mid 中继续查找,找到更大的mid。
所以我们可以设计出如下判定条件:
double pd(double a,int m)
{double c=1;while(m>0) //计算a的m次方{c=c*a;m--;}if(c>=n) return true;elsereturn false;
}
代码解答
#include <cstdio>
#include <iostream>
#include<iomanip> //用于浮点数输出
using namespace std;double n,l,r,mid;
double eps=1e-8;bool pd(double a,int m)
{double c=1;while(m>0) {c=c*a;m--;}if(c>=n) //return true;elsereturn false;
}int main()
{int m;cin>>n>>m;
//设置二分边界l=0,r=n;//实数二分while (l + eps < r){double mid = (l + r) / 2;if (pd(mid,m))r = mid;elsel = mid;}cout << fixed << setprecision(7) << l;//一般使用print//printf("%x.yf",n)//其中X是固定整数长度,小数点前的整数位数不够,会在前面补0//y是保留小数位数,不够补零//printf("%.7f",l);return 0;
}
分巧克力
2017 年省赛真题链接。
题目描述: 儿童节那天有 K 位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有 N 块巧克力,其中第 i 块是 Hi×Wi 的方格组成的长方形。为了公平起见,
小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。切出的巧克力需要满足:
- 形状是正方形,边长是整数;
- 大小相同;
例如一块 6x5 的巧克力可以切出 6 块 2x2 的巧克力或者 2 块 3x3 的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小明计算出最大的边长是多少么?
输入描述:
第一行包含两个整数 N,K (1≤N,K≤10^5)。
以下 N 行每行包含两个整数 Hi,Wi (1≤Hi,Wi≤10^5)。
输入保证每位小朋友至少能获得一块 1x1 的巧克力。
输出描述:
输出切出的正方形巧克力最大可能的边长。
输入输出样例:
示例:
输入
2 10 6 5 5 6
输出
2
运行限制:
- 最大运行时间:2s
- 最大运行内存: 256M
注意:
- 请严格按要求输出,不要画蛇添足地打印类似:“请您输入…”的多余内容。
- 不要调用依赖于编译环境或操作系统的特殊函数。
- 所有依赖的函数必须明确地在源文件中
- 不能通过工程设置而省略常用头文件。
题目分析
简单思路,边长的最大规模为 100000;我们可以枚举出所有的情况。按从大到小的顺序进行切割,直到找到满足要求的巧克力边长。
在判断边长是否满足条件时:求一块长方形(h∗w)最多被分成的正方形(len∗len)巧克力个数为:
cnt=(h/len)∗(w/len)
但是使用朴素算法枚举时间复杂度O(n)∗O(n)=O(n^2) 会超时,所以改用 2 分查找法,这找到符合要求的最大的一个。
即用在单调递增序列 a 中查找 <=x 的数中最大的一个(即 x 或 x 的前驱)即可,原本这里的条件是 <=x ,我们将其换成验证即可。
代码解答
#include<bits/stdc++.h>using namespace std;
const int MAXN=100010;
int n,k;
int h[MAXN],w[MAXN];bool pd(int l)
{int sum=0;for(int i=0; i<n; i++){sum+=(h[i]/l)*(w[i]/l);if(sum>=k){return true;}}return false;
}int main()
{cin>>n>>k;for(int i=0; i<n; i++)cin>>h[i]>>w[i];//找到二分查找的上界int high=0;for(int i=0; i<n; i++){high=max(high,h[i]);high=max(high,w[i]);}// 二分下届由题意可得至少为1int low=1;// 由于本题目就是求符合要求的Mid 值所以要将mid定义在二分查找外边int mid=0;while(low<high){mid = (low + high+1) / 2;if(pd(mid))low=mid;elsehigh = mid - 1;// cout<<low<<" "<<high<<endl;}//因为low=high所以输出哪一个都一样cout<<low;return 0;
}
相关文章:

【No.13】蓝桥杯二分查找|整数二分|实数二分|跳石头|M次方根|分巧克力(C++)
二分查找算法 知识点 二分查找原理讲解在单调递增序列 a 中查找 x 或 x 的后继在单调递增序列 a 中查找 x 或 x 的前驱 二分查找算法讲解 枚举查找即顺序查找, 实现原理是逐个比较数组 a[0:n-1] 中的元素,直到找到元素 x 或搜索整个数组后确定 x 不在…...
【蓝桥杯-单片机】基于定时器的倒计时程序设计
基于定时器的倒计时程序 题目如下所示: 实现过程中遇到的一些问题 01 如何改变Seg_Buf数组的值数码管总是一致地显示0 1 2 3 4 5 首先这个问题不是在main.c中关于数码管显示部分的逻辑错误,就是发生在数码管的底层错误。 检查了逻辑部分ÿ…...
QT:三大特性
QT的三大特性: 1、信号与槽 2、内存管理 3、事件处理 1、信号与槽 当信号产生时,就会自动调用绑定的槽函数。 自定义信号: 类中需要添加O_OBJECT宏 声明: signals标签之下进行声明 定义: 信号不需要定义 …...

无服务器推理在大语言模型中的未来
服务器无服务器推理的未来:大型语言模型 摘要 随着大型语言模型(LLM)如GPT-4和PaLM的进步,自然语言任务的能力得到了显著提升。LLM被广泛应用于聊天机器人、搜索引擎和编程助手等场景。然而,由于LLM对GPU和内存的巨大需求,其在规…...

【linux】CentOS查看系统信息
一、查看版本号 在CentOS中,可以通过多种方法来查看版本号。以下是几种常用的方法: 使用cat命令查看/etc/centos-release文件: CentOS的版本信息存储在/etc/centos-release文件中。可以使用cat命令来显示该文件的内容,从而获得C…...

部署dagu_1.12.10+replicadb0.15.1+sqlline1.12
下载所需的文件并上传到服务器 dagu_1.12.10(选择适合自己的版本): https://gh.api.99988866.xyz/https://github.com/dagu-dev/dagu/releases/download/v1.12.10/dagu_1.12.10_linux_amd64.tar.gzreplicadb0.15.1(包含了sqlline1.12): https://download.csdn.net/download/u0…...
基于Java中的SSM框架实现社会保险管理系统项目【项目源码+论文说明】
摘要 改革开放的浪潮已近深深的键入人心,随之而带来了我国社会主义市场经济体制的不断完善和建立健全,作为国家基本保障之一的社会保险系统,我们不单单要把握社保金额的进展和状态,还需要对社会保障基金开展全面、科学、可持续的…...

24计算机考研调剂 | 江西理工大学
能源、化工、计算机(0854)等相关方向有3个调剂名额 考研调剂招生信息 学校:江西理工大学 专业:工学->治金工程 年级:2024 招生人数:3 招生状态:正在招生中 联系方式:********* (为保护个人隐私,联系方式仅限APP查看) 补充内容 能源、化工、计…...

Sentry(Android)源码解析
本文字数:16030字 预计阅读时间:40分钟 01 前言 Sentry是一个日志记录、错误上报、性能监控的开源框架,支持众多平台: 其使用方式在本文不进行说明了,大家可参照官方文档:https://docs.sentry.io/platforms…...

Android StateLayout状态页
文章目录 Android StateLayout状态页概述源码使用源码下载 Android StateLayout状态页 概述 StateLayout(状态页)包含:加载中页面,错误页面,空页面,内含状态默认页面,支持自定义页面。 源码 …...
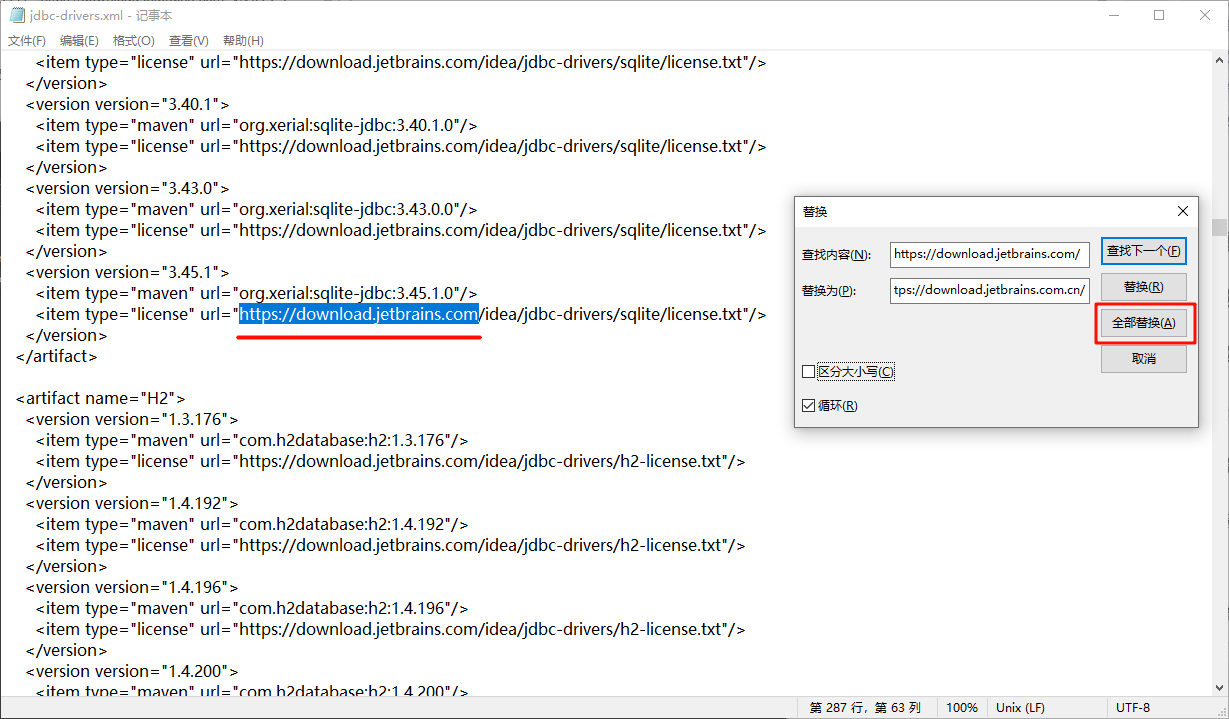
JetBrains数据库驱动下载失败解决方法
本方法可通用于解决PyCharm等JetBrains家的IDE下载数据库驱动问题。 在Jet家IDE内连接数据库时,mysql、sqlite等的驱动有部分在 https://download.jetbrains.com 网站上,可能由于网络问题无法访问。 解决方法是修改 JetBrains 路径下的 jdbc.drivers.xm…...

【vim 学习系列文章 16 -- vim 自动保存设置】
文章目录 vim 自动保存设置 vim 自动保存设置 在 Vim 编辑器中,你可以通过设置 updatetime 选项来控制自动保存的时间间隔。updatetime 的默认值是 4000 毫秒(4 秒),但你可以将其设置为 5000 毫秒(5 秒)以…...

python的O2O生鲜食品订购flask-django-nodejs-php
用户只能通过一些类似软件进行查看生鲜超市,这样的管理方式仍然是比较机械传统的,本文通过对市面上常见的线上管理系统与现实生活中结合问题的讨论,从一个微信小程序的O2O生鲜食品订购角度进行需求分析,提供一些新的思路ÿ…...

六、大模型-Prompt-API介绍
GPT-3.5 API 提供了一个名为 openai.ChatCompletion.create() 的端点,您可以使用该端点来与 ChatGPT 进行交互。以下是 openai.ChatCompletion.create() 的详细 API 说明: 请求参数: messages:一个数组,包含对话中的消…...
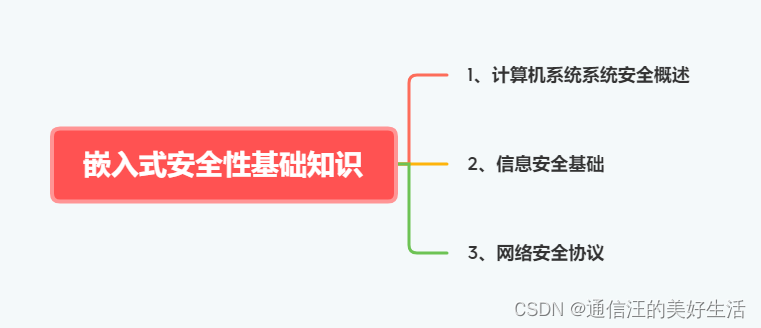
嵌入式安全性基础知识-计算机系统安全知识+信息安全基础+网络安全协议-嵌入式系统设计师备考笔记
0、前言 本专栏为个人备考软考嵌入式系统设计师的复习笔记,未经本人许可,请勿转载,如发现本笔记内容的错误还望各位不吝赐教(笔记内容可能有误怕产生错误引导)。 本章的主要内容见下图: 1、计算机系统系统…...
基于javaSpringboot+mybatis+layui的装修验收管理系统设计和实现
基于javaSpringbootmybatislayui的装修验收管理系统设计和实现 博主介绍:多年java开发经验,专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 央顺技术团队 Java毕设项目精品实战案例《1000套》 欢迎点赞 收藏 ⭐留…...
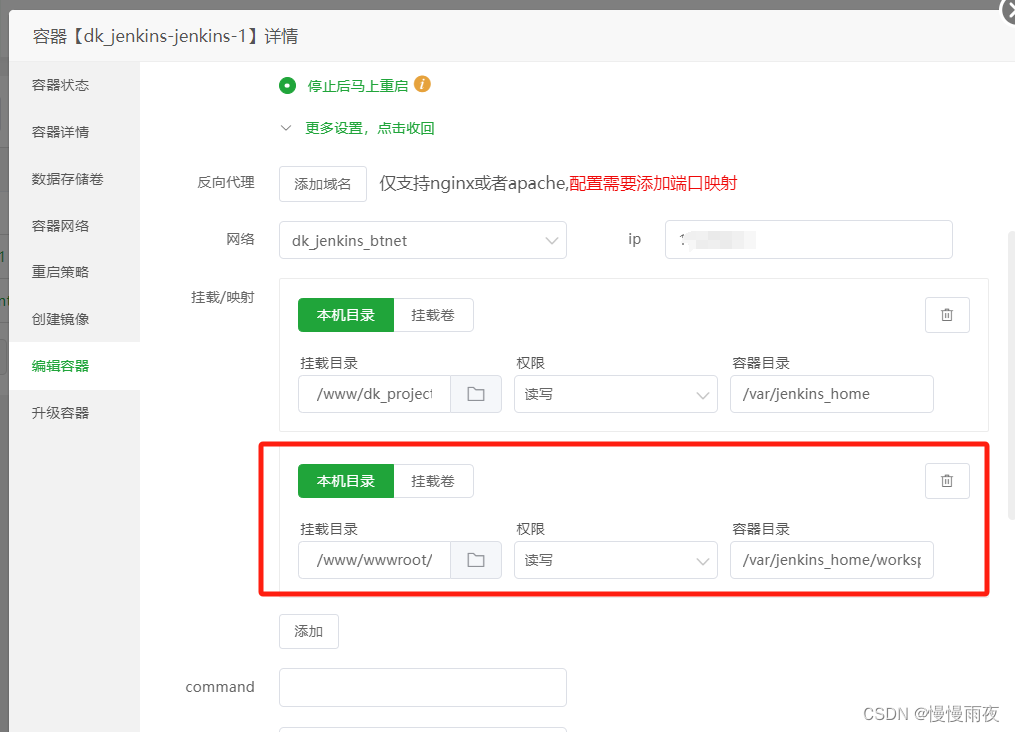
jenkins构建完成后部署到本机,无法读取容器外文件夹
项目背景: Dockerjenkins 构建完成后,要把打包的dist文件夹内容移动到网站目录 /www/wwwroot/xxxxxx 文件夹下;但是获取不到jenkins容器外的文件夹。 解决办法: 在容器中,添加挂载/映射本机目录,把网站…...
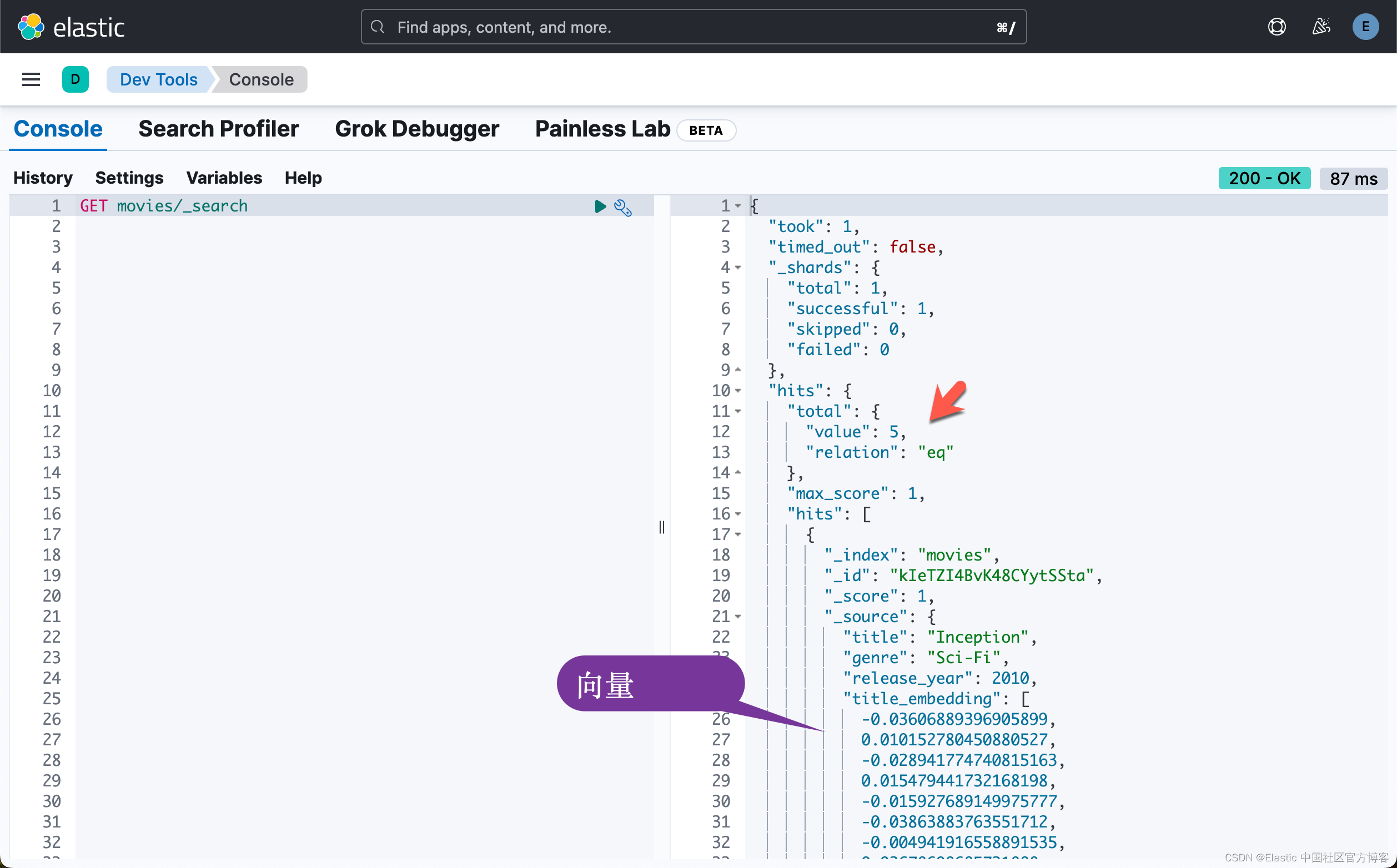
如何使用 Elasticsearch 作为向量数据库
在今天的文章中,我们将很快地通过 Docker 来快速地设置 Elasticsearch 及 Kibana,并设置 Elasticsearch 为向量搜索。 拉取 Docker 镜像 docker pull docker.elastic.co/elasticsearch/elasticsearch:8.12.2 docker pull docker.elastic.co/kibana/kiba…...

高精度AI火灾烟雾检测算法,助力打造更加安全的楼宇环境
一、方案背景 近日,南京居民楼火灾事故导致15人死亡的新闻闹得沸沸扬扬,这一事件又激起了大家对楼宇火灾隐患的进一步担忧。事后我们除了思考政府、消防及物业部门应对此事的解决办法,我们还应该思考如何利用现有的技术帮助人们减少此类事情的…...

node和npm yarn包管理工具
node和包管理工具 今日目标: 1.dos常用指令 2.node的模块化 3.npm包管理工具 4.yarn的常用指令 5.node的内置模块 00-回顾 # Promose:作用:解决ajax请求响应顺序不可控的问题特性:1. Promise是一个构造函数,需要通过new关…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
