0103设计算法-算法基础-算法导论第三版
文章目录
- 一、分治法
- 二、分析分治算法
- 结语
我们可以选择使用的算法设计技术有很多。插入排序使用了增量方法:在排序子数组 A [ 1 ⋯ j − 1 ] A[1\cdots j-1] A[1⋯j−1]后,将单个元素 A [ j ] A[j] A[j]插入子数组的适当位置,产生排序好的子数组 A [ 1 ⋯ j ] A[1\cdots j] A[1⋯j]。
下面我们学习称为“分治法”的设计方法。
一、分治法
许多有用的算法在结构上是递归的:为了解决一个问题,算法一次或者多次调用其自身以解决紧密相关的若干子问题。
这些算法典型地遵循分治法的思想:将原问题分解为几个规模较小但类似于原问题的子问题,递归地求解这些子问题的解,然后在合并这些子问题的解来建立原问题的解。
分治模式在每层递归时都有三个步骤:
- 分解原问题为若干子问题,这些子问题是原问题的规模较小的实例。
- 解决这些子问题,递归地求解各子问题。然后,若子问题的规模足够小,则直接求解。
- 合并这些子问题的解成原问题的解。
归并排序算法完全遵循分治模式。直观上其操作如下:
- 分解:分解待排序的n个元素的序列成各具有 n 2 \frac{n}{2} 2n个元素的两个子序列。
- 解决:使用归并排序递归地排序两个子序列。
- 合并:合并两个已排序的子序列以产生已排序的答案。
递归终止条件:当待排序的序列长度为1,递归“开始回升”,长度为1的每个序列都已排好序。
归并排序算法的关键操作是“合并”步骤中两个已排序序列的合并。我们通过一个辅助过程MERGE(A,p,q,r)来完成合并,其中A是一个数组,p、q和r是数组的下标,满足 p ≤ q < r p\le q\lt r p≤q<r。该过程假设子数组 A [ p ⋯ q ] 和 A [ q + 1 ⋯ r ] A[p\cdots q]和A[q+1\cdots r] A[p⋯q]和A[q+1⋯r]以排好序。它合并这两个子数组形成单一的已排好序的子数组并代替当前的子数组 A [ p ⋯ r ] A[p\cdots r] A[p⋯r]。
过程MERGE需要 O ( n ) O(n) O(n)的时间,其中 n = r − p + 1 n=r-p+1 n=r−p+1是待合并元素的总和。为避免在每个基本步骤必须检查是否有堆为空,我们在每个堆的底部放置一个哨兵,它包含一个特殊的值,用于简化代码。这里我们使用 ∞ \infty ∞作为哨兵值,它不可能为较小的值,除非两个堆都已显露出其哨兵值。下面的伪代码实现MERGE
MERGE(A,p,q,r)
1 n1=q-r+1
2 n2=r-q
3 let L[1...n1+1] and R[1...n2+1] be new arrays
4 for i = 1 to n1
5 L[i] = A[p+i-1]
6 for j = 1 to n2
7 R[j] = A[q+j]
8 L[n1+1]=无穷
9 R[n2+1]=无穷
10 i = 1
11 j = 1
12 for k = p to r
13 if L[i] <= R[j]
14 A[k] = l[i]
15 i = i + 1
16 else A[k] = R[j]
17 j = j + 1
我们需要证明第12~17行for循环的第一次迭代之前该循环不变式成立,该循环每次迭代保持该不变式,并且循环终止时,该不变式提供了一种有用的性质来证明正确性。
初始化:循环的第一次迭代之前,有 k = p k=p k=p,所以子数组 A [ p ⋯ k − 1 ] A[p\cdots k-1] A[p⋯k−1]为空。这个空的子数组包含L和R的 k = p = 0 k=p=0 k=p=0歌最小元素。又因为 i = j = 1 i=j=1 i=j=1,所以 L [ i ] 和 R [ j ] L[i]和R[j] L[i]和R[j]都是各自所在数组中未被复制回数组A的最小元素。
保持:为了理解每次迭代都维持选好不变式,首选假设 L [ i ] ≤ R [ j ] L[i]\le R[j] L[i]≤R[j].这时, L [ i ] L[i] L[i]是未被复制回数组A的最小元素。因为 A [ p ⋯ k − 1 ] A[p\cdots k-1] A[p⋯k−1]包含 k − p k-p k−p个最小元素,所以在第14行将 L [ i ] L[i] L[i]复制到 A [ k ] A[k] A[k]之后,子数组 A [ p ⋯ k ] A[p\cdots k] A[p⋯k]将包含 k − p + 1 k-p+1 k−p+1个最小子元素。增加k的值(在for循环中更新)和 i i i的值后,为下次迭代重新建立了该循环不变式。反之,若 L [ i ] > R [ j ] L[i]\gt R[j] L[i]>R[j],则第16~17行执行适当的操作来维持该循环不变式。
终止:终止时, k = r + 1 k=r+1 k=r+1。根据循环不变式,子数组 A [ p ⋯ k − 1 ] A[p\cdots k-1] A[p⋯k−1]就是 A [ p ⋯ r ] A[p\cdots r] A[p⋯r]且按从小到大的顺序包含 L [ 1 ⋯ n 1 + 1 ] 和 R [ 1 ⋯ n 2 + 1 ] L[1\cdots n1+1]和R[1\cdots n2+1] L[1⋯n1+1]和R[1⋯n2+1]中的 k − p = r − p + 1 k-p=r-p+1 k−p=r−p+1个最小的元素数组L和R一起包含 n 1 + n 2 + 2 = r − p + 3 n1+n2+2=r-p+3 n1+n2+2=r−p+3个元素。处两个最大的元素以为,其他所有元素都已被复制回数组A,这两个最大的元素是哨兵。
过程MERGE的运行时间是 O ( n ) ,其中 n = r − p + 1 O(n),其中n=r-p+1 O(n),其中n=r−p+1。第1-3行和第8-11行中的每行都需要常量时间,第4-7行的for循环需要 O ( n 1 + n 2 ) = O ( n ) O(n1+n2)=O(n) O(n1+n2)=O(n)的时间,第12-17行的for循环有n次迭代,每次迭代需要常量时间。
现在我们keyiBaby过程MERGE做为归并排序的一个子程序来用。下面的过程MERGE-SORT(A,p,r)排序子数组 A [ p ⋯ r ] A[p\cdots r] A[p⋯r]中的元素。若 p ≥ r p\ge r p≥r,则该数组最多有1个元素,所以已经排好序。否则,分解步骤简单地计算一个下标q,将 A [ p ⋯ r ] A[p\cdots r] A[p⋯r]分解成两个子数组 A [ p ⋯ q ] 和 A [ q + 1 ⋯ r ] A[p\cdots q]和A[q+1\cdots r] A[p⋯q]和A[q+1⋯r],前者包含 ⌈ n 2 ⌉ \lceil \frac{n}{2}\rceil ⌈2n⌉个元素,后者包含 ⌈ n 2 ⌉ \lceil \frac{n}{2}\rceil ⌈2n⌉个元素。
MERGE-SORT(A,p,r)
1 if p < r
2 q=floor((p+r)/2)
3 MERGE-SORT(A,p,q)
4 MERGE_SORT(A,q+1,r)
5 MERGE(A,p,q,r)
为了排序整个序列 A ( A [ 1 ] , A [ 2 ] , ⋯ , A [ n ] ) A(A[1],A[2],\cdots,A[n]) A(A[1],A[2],⋯,A[n]),我们执行初始调用MERGE-SORT(A,1,A.length),这里再次有 A . l e n g t h = n A.length=n A.length=n。下图索命了当n位2的幂时该操作的过程。
算法分为分解和合并两部分。
分解:把长度为n的序列分解为 n 2 \frac{n}{2} 2n的两个子序列,在把长度为 n 2 \frac{n}{2} 2n的子序列分解为 n 4 \frac{n}{4} 4n的子序列,直至子序列长度为1.
合并:合并只含1项的序列形成长度为2的排好序的序列,合并长度为2的序列形成长度为4的排好序的序列,依此下去,直到长度为 n 2 \frac{n}{2} 2n的两个序列被合并最终成都为n的排好序的序列。

二、分析分治算法
当一个算法包含对其自身的递归调用时,我们往往可以用递归方程或递归式来描述其运行时间,该方程根据在较小输入上的运行时间来描述在规模为n的问题上的总运行时间。然后,我们可以使用数学工具来求解该递归式并给出算法性能的界。
分治算法运行时间的递归式来自基本模式的三个步骤。如前所述,我们假设 T ( n ) T(n) T(n)是规模为n的一个问题的运行时间。若问题规模足够小,如对某个常量 c , n ≤ c c,n\le c c,n≤c,则直接求解需要常量时间,我们将其写作 O ( 1 ) O(1) O(1)。假设把原问题分解为 a a a个子问题,没个子问题的规模是原问题的 1 b \frac{1}{b} b1为了求解一个规模 n b \frac{n}{b} bn的子问题,需要 T ( n b ) T(\frac{n}{b}) T(bn)的时间,所以需要 a T ( n b ) aT(\frac{n}{b}) aT(bn)的时间求解a个子问题。如果分解问题成子问题需要时间D(n),合并子问题的解成原问题的解需要时间为C(n),那么得到递归式
T ( n ) = { O ( 1 ) , 若 n ≤ c a T ( n b ) + D ( n ) + C ( n ) 其他 T(n)=\begin{cases} O(1),若n\le c\\ aT(\frac{n}{b})+D(n)+C(n)\quad 其他 \end{cases} T(n)={O(1),若n≤caT(bn)+D(n)+C(n)其他
归并排序算法的分析
虽然MERGE-SORT的伪代码在运算的数量不是偶数时也能正常工作,但是,如果假定原问题规模是2的幂,那么基于递归式的分析将被简化。在第4章,我们将看到这个假设不影响递归式解的增长量级。
下面我们分析建立归并排序n个数的最坏情况下的运行时间T(n)的递归式。归并排序一个元素需要长时间。当有 n > 1 n\gt 1 n>1个元素时,我们分解运行时间如下:
分解:分解步骤仅仅计算子数组的中间位置,需要常量时间,因此,D(n)=O(1)。
解决:我们递归求解两个规模为 n 2 \frac{n}{2} 2n的子问题,运行时间为 2 T ( n 2 ) 2T(\frac{n}{2}) 2T(2n)
合并: 在一个具有n个元素的子数组上过程MERGE需要O(n)的时间,所以C(n)=O(n)。
把分析结果带入上述递归式,有
T ( n ) = { O ( 1 ) , 若 n = 1 2 T ( n 2 ) + O ( n ) , n > 1 T(n)=\begin{cases} O(1),若n = 1\\ 2T(\frac{n}{2})+O(n),n\gt 1 \end{cases} T(n)={O(1),若n=12T(2n)+O(n),n>1
在第4章,我们将看到“主定理”,可以用改定理证明 T ( n ) = O ( n lg n ) , 起咋 lg n 代表 log 2 n T(n)=O(n\lg n),起咋\lg n 代表\log_2 n T(n)=O(nlgn),起咋lgn代表log2n。
因为对数函数比任何线性函数增长要慢,所以对足够大的输入,在最坏情况下,运行时间 O ( n lg n ) O(n\lg n) O(nlgn)的归并排序将优于运行时间诶 O ( n 2 ) O(n^2) O(n2)的插入排序。
算法实现及优化(在输入规模小于某个阈值时,使用插入排序)见下面链接2.
结语
欢迎小伙伴一起学习交流,需要啥工具或者有啥问题随时联系我。
❓QQ:806797785
⭐️源代码地址:https://gitee.com/gaogzhen/algorithm
[1]算法导论(原书第三版)/(美)科尔曼(Cormen, T.H.)等著;殷建平等译 [M].北京:机械工业出版社,2013.1(2021.1重印).p16-22
[2]归并排序-排序-算法第四版[CP/OL]
相关文章:

0103设计算法-算法基础-算法导论第三版
文章目录 一、分治法二、分析分治算法结语 我们可以选择使用的算法设计技术有很多。插入排序使用了增量方法:在排序子数组 A [ 1 ⋯ j − 1 ] A[1\cdots j-1] A[1⋯j−1]后,将单个元素 A [ j ] A[j] A[j]插入子数组的适当位置,产生排序好的子…...

[NCTF2019]SQLi ---不会编程的崽
欸嘿,继续sql注入。又是新的sql注入类型 很直接哦,给出了sql查询语句。简单扫描一下,robots.txt还能访问。里边提示hint.txt $black_list "/limit|by|substr|mid|,|admin|benchmark|like|or|char|union|substring|select|greatest|%00…...

上位机开发 halcon坐标转轴坐标
背景 上位机开发中有一种相机叫标定相机,主要是有来给某些要进行根据CAD图点位计算时当前产品实际点位坐标时使用的一种标定测量相机。主要原理是根据两个或多个指定的标定点进行取图计算圆心坐标,再将视觉计算出的圆心坐标和取图时的轴坐标进行偏差计算。最后得到标定点轴的…...

[数据结构]二叉树(下)
一、二叉树的节点和深度关系 1.满二叉树 我们可以假设二叉树有N个节点,深度为h我们可以恒容易得到满二叉树每行的节点数,然后错位相减,算出节点与高度的关系。 2.完全二叉树 注意我这个是因为最后一行的节点数为1。 二、向上调整建堆和向下调整建堆的时…...

动手学深度学习|notebook教程
D2L.AI|《动手学深度学习》Notebooks 目录 面向中文读者的能运行、可讨论的深度学习教科书 含 PyTorch、NumPy/MXNet、TensorFlow 和 PaddlePaddle 实现 被全球 70 多个国家 500 多所大学用于教学 github 下面是整理好的,可以直接运行的notebook 0 前…...

C#面:简述 .NET Framework 类库中的“命名空间”
在 C# 中,命名空间(Namespace)是一种用于组织和管理代码的机制。它提供了一种将相关的类、接口、结构体和其他类型组织在一起的方式,以便更好地管理和维护代码。 .NET Framework类库中的命名空间是一种逻辑上的分组,它…...
android.os.TransactionTooLargeException解决方案,Kotlin
android.os.TransactionTooLargeException解决方案,Kotlin 首先,特意制造一个让Android发生TransactionTooLargeException的场景,一个Activity启动另外一个Activity,在Intent的Bundle里面塞入一个大的ArrayList: import android.…...
ChatGPT智能聊天系统源码v2.7.6全开源Vue前后端+后端PHP
测试环境:Linux系统CentOS7.6、宝塔、PHP7.4、MySQL5.6,根目录public,伪静态thinkPHP,开启ssl证书 具有文章改写、广告营销文案、编程助手、办公达人、知心好友、家庭助手、出行助手、社交平台内容、视频脚本创作、AI绘画、思维导图等功能 ai通道:文心一言、MiniMax、智…...
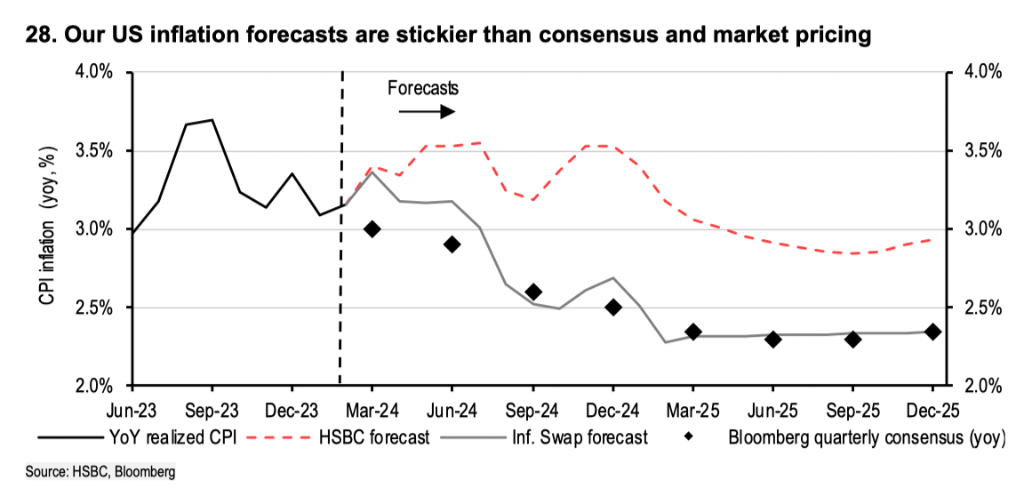
汇丰:当前的美股是泡沫吗?
汇丰认为,当前的风险资产并不构成泡沫,更类似于2017年的市场环境,风险资产有望继续稳步上升。 隔夜美股飙涨,标普创三个月最大周涨,纳指收盘创历史新高。结合去年以来的强劲表现,有观点认为由科技股支撑的…...

颠覆传统:Web3如何塑造未来的数字经济
引言 近年来,随着数字化时代的到来,互联网已经成为人们生活中不可或缺的一部分。然而,随着技术的不断发展和社会的不断变迁,传统的Web2模式逐渐显露出一些弊端,如数据垄断、隐私泄露等问题,这促使人们寻求…...
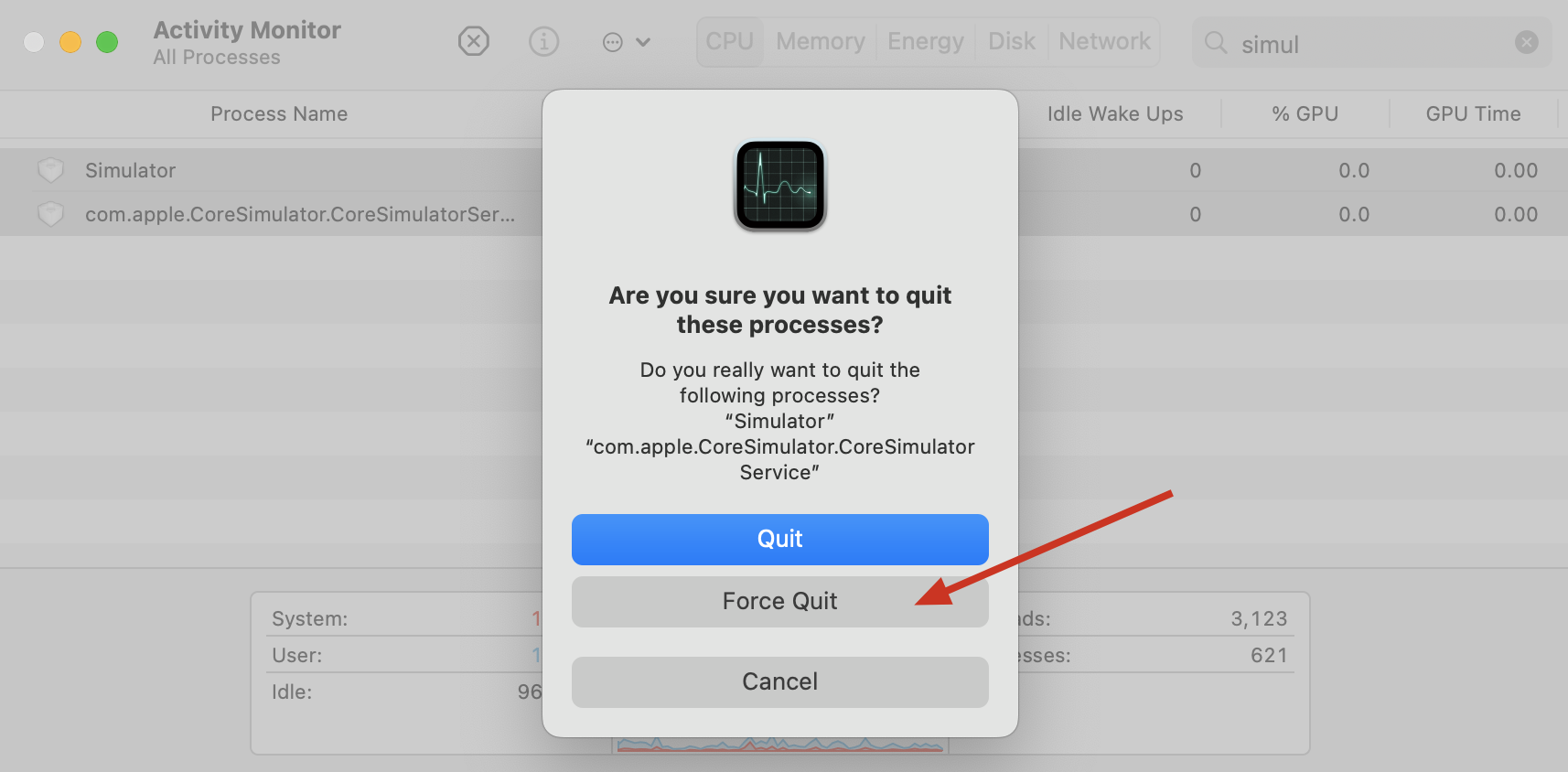
iOS模拟器 Unable to boot the Simulator —— Ficow笔记
本文首发于 Ficow Shen’s Blog,原文地址: iOS模拟器 Unable to boot the Simulator —— Ficow笔记。 内容概览 前言终结模拟器进程命令行改权限清除模拟器缓存总结 前言 iOS模拟器和Xcode一样不靠谱,问题也不少。😂 那就有病治…...

使用 Flink + Faker Connector 生成测试数据压测 MySQL
博主历时三年精心创作的《大数据平台架构与原型实现:数据中台建设实战》一书现已由知名IT图书品牌电子工业出版社博文视点出版发行,点击《重磅推荐:建大数据平台太难了!给我发个工程原型吧!》了解图书详情,…...

Android单片机硬件通信《GPIO通信》
一、什么是GPIO? GPIO(英语:General-purpose input/output),通用型输入输出端口,在单片机上一般是通过一个GND引脚和若干个io引脚配合工作。 单片机可以配置GPIO输入输出模式,与外界环境进行通信交互。在输入环境下&…...
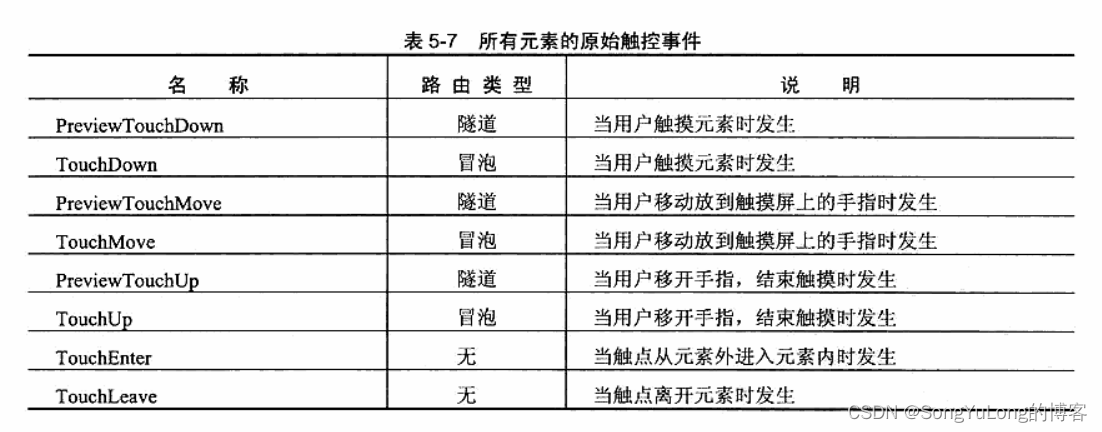
C# WPF编程-事件
C# WPF编程-路由事件 路由事件概要路由事件的三种方式 WPF事件WPF最重要的5类事件:生命周期事件 鼠标事件键盘事件多点触控输入原始触控 路由事件概要 路由事件是具有更强传播能力的事件,它们可在元素树中向上冒泡和向下隧道传播,并沿着传播…...

C语言 预处理器 注释 基本案例讲解
上文 程序设计语言与C语言发展 我们简述了 计算机语言的发展 以及编程语言与指令的概念 那么 今天 我们就来 初始C语言 并完成 第一个C语言案例 这里 我们需要完成 C语言 Hello World案例 以及 C语言程序举例 任何编程语言 开始的案例 都是 Hello World 所以说 Hello World 是…...

Flutter学习10 - Json解析与Model使用
对于网络请求返回的 Json 数据,一般会进行如下解析: 将 Json String 解析为 Map<String, dynamic>将 Json String 解析为 Dart Model 发起一个返回 Json String 的网络请求 import package:http/http.dart as http;void main() {_doGet(); }_do…...
 and Float64)
Clickhouse异常:Exception: No operation equals between Decimal(X, X) and Float64
在使用clickhouse中的Decimal类型存储数字时,使用Decimal类型字段作为查询条件时,比如: SELECT COUNT(*) AS total FROM table WHERE ( my_number10.2) 会报错如下:Exception: No operation equals between Decimal(X, X) and F…...
会员中心微服务
文章目录 1.环境配置1.创建会员中心模块2.检查父子模块的pom.xml1.父模块注意:如果父模块中的依赖显示not found,原因是子模块并没有引用,不用在意 2.子模块 3.pom.xml 引入相关依赖(别忘记刷新maven)4.application.ym…...

element el-dialog里再调用其他组件,查找不到组件的方法
需求描述:点击编辑按钮,跳出编辑弹窗,回显图片组件里面的图片问题:element el-dialog里再调用组件,打开该弹窗的瞬间找不到弹窗里调用子组件的方法原因:弹窗显示时,调用的子组件还没渲染出来所以…...
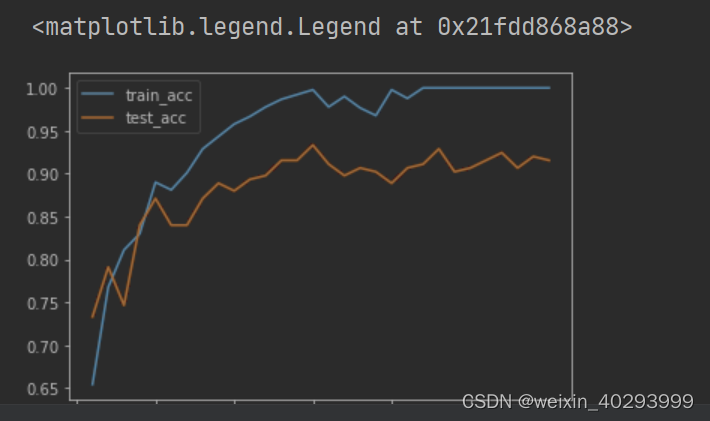
【深度学习】四种天气分类 模版函数 从0到1手敲版本
引入该引入的库 import torch import torch.nn as nn import matplotlib.pyplot as plt import torch.nn.functional as F import torchvision import torch.optim as optim %matplotlib inline import os import shutil import glob os.environ["KMP_DUPLICATE_LIB_OK&q…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
