Eureka和Nacos的关系
目录
它们的比较:
结论:
Eureka和Nacos都是服务发现和注册中心,它们在微服务架构中扮演着关键角色,但它们是由不同的组织开发的,服务于类似但不完全相同的目的。以下是它们之间的关系:
-
Eureka:
- 开发者:Eureka是由Netflix开发的,作为Spring Cloud Netflix的一部分广泛使用。
- 功能:它主要用于服务注册和发现,允许微服务实例在启动时注册自己,并与其他服务通信。
- 架构:Eureka采用的是AP(可用性/分区容忍性)模型,它可以很好地处理网络分区问题,保证服务的可用性。
-
Nacos:
- 开发者:Nacos是由阿里巴巴开发的,是一个更全面的服务基础设施,支持服务发现、配置管理和服务管理。
- 功能:除了服务发现和注册功能,Nacos还提供了动态配置服务、服务管理等功能,支持灰度发布等。
- 架构:Nacos旨在提供CP(一致性/分区容忍性)和AP模式的切换能力,以适应不同的场景需求。
它们的比较:
- 技术栈兼容性:Eureka更多地与Spring Cloud生态系统集成,而Nacos虽然也可以与Spring Cloud集成,但它是独立于Spring Cloud生态的。
- 功能范围:Nacos提供了比Eureka更广泛的功能,不仅限于服务发现和注册。
- 项目状态:Netflix在2018年宣布Eureka 2.0项目进入维护模式,并不再积极开发新功能。而Nacos作为一个活跃的项目,持续得到更新和功能扩展。
- 社区和支持:Nacos作为一个较新的项目,拥有活跃的社区和来自阿里巴巴的强大支持,而Eureka作为一个成熟的项目,有广泛的使用基础和社区支持,但新功能的增加可能有限。
结论:
Eureka和Nacos虽然都是服务发现和注册中心,但它们由不同的组织开发,各自有独特的特点和功能范围。用户在选择时应根据自己的需求以及与现有技术栈的兼容性来决定使用哪一个。随着Spring Cloud Alibaba的发展,Nacos在Spring Cloud生态中的地位逐渐上升,为开发者提供了更多选择。
相关文章:

Eureka和Nacos的关系
目录 它们的比较: 结论: Eureka和Nacos都是服务发现和注册中心,它们在微服务架构中扮演着关键角色,但它们是由不同的组织开发的,服务于类似但不完全相同的目的。以下是它们之间的关系: Eureka:…...
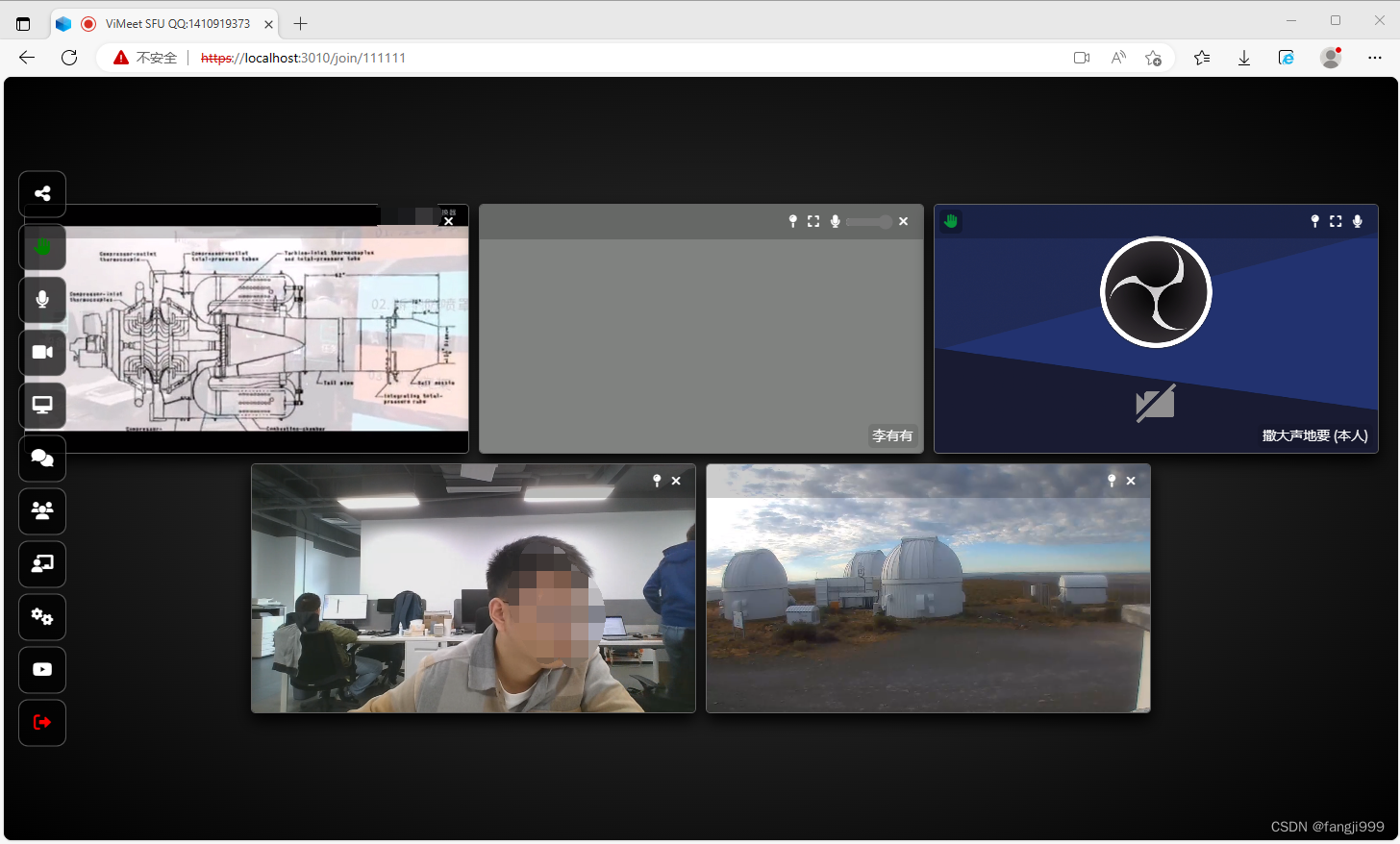
极简自建web视频会议,私有云,rtmp/rtsp/webrtc一键参会直播会议互动方案
随着视频互动深入工作日常,很多客户需要自建一个会议,监控的交互平台,目前外面不管是开源还是非开源的平台,都是极为复杂,一般linux安装库关联部署复杂,非技术人员根本没办法使用,不方便集成部署…...
5G智能网关助力工业铸造设备监测升级
随着物联网技术的迅猛发展和工业4.0浪潮的推进,传统工业正面临着严峻的转型升级压力。在这一背景下,铸造行业——这一典型的传统重工业领域,也必须积极探索借助5G、物联网、边缘计算等技术提升生产经营效率的新路径。 本文就基于佰马合作伙伴…...

奇舞周刊第523期:来自 rust 生态的强烈冲击?谈谈 Leptos 在语法设计上的精妙之处...
奇舞推荐 ■ ■ ■ 来自 rust 生态的强烈冲击?谈谈 Leptos 在语法设计上的精妙之处 过去很长一段时间,前端框架们都在往响应式的方向发展。同时又由于 React hooks 的深远影响,函数式 响应式成为了不少前端心中最理想的前端框架模样。Solid …...

《边缘计算:连接未来的智慧之桥》
随着物联网、5G等技术的快速发展,边缘计算作为一种新兴的计算模式,正逐渐引起人们的广泛关注。边缘计算通过将数据处理和存储功能放置在距离数据产生源头更近的位置,实现了更快速、更可靠的数据处理和交换,为各行各业带来了前所未…...

php 各种魔术函数的触发条件
2024.3.20 1、__construct() __construct() 用于在创建对象时自动触发 当使用 new 关键字实例化一个类时,会自动调用该类的 __construct() 方法 <?php class MyClass {public function __construct() {echo "已触发 __construct 一次";} }$obj new …...

Linux的学习之路:2、基础指令(1)
一、ls指令 上篇文章已经说了一点点的ls指令,不过那还是不够的,这篇文章会介绍更多的指令,最起码能使用命令行进行一些简单的操作,下面开始介绍了 ls常用选项 -a 列出目录下的所有文件,包括以 . 开头的隐含文件。 -d…...

0103设计算法-算法基础-算法导论第三版
文章目录 一、分治法二、分析分治算法结语 我们可以选择使用的算法设计技术有很多。插入排序使用了增量方法:在排序子数组 A [ 1 ⋯ j − 1 ] A[1\cdots j-1] A[1⋯j−1]后,将单个元素 A [ j ] A[j] A[j]插入子数组的适当位置,产生排序好的子…...

[NCTF2019]SQLi ---不会编程的崽
欸嘿,继续sql注入。又是新的sql注入类型 很直接哦,给出了sql查询语句。简单扫描一下,robots.txt还能访问。里边提示hint.txt $black_list "/limit|by|substr|mid|,|admin|benchmark|like|or|char|union|substring|select|greatest|%00…...

上位机开发 halcon坐标转轴坐标
背景 上位机开发中有一种相机叫标定相机,主要是有来给某些要进行根据CAD图点位计算时当前产品实际点位坐标时使用的一种标定测量相机。主要原理是根据两个或多个指定的标定点进行取图计算圆心坐标,再将视觉计算出的圆心坐标和取图时的轴坐标进行偏差计算。最后得到标定点轴的…...

[数据结构]二叉树(下)
一、二叉树的节点和深度关系 1.满二叉树 我们可以假设二叉树有N个节点,深度为h我们可以恒容易得到满二叉树每行的节点数,然后错位相减,算出节点与高度的关系。 2.完全二叉树 注意我这个是因为最后一行的节点数为1。 二、向上调整建堆和向下调整建堆的时…...

动手学深度学习|notebook教程
D2L.AI|《动手学深度学习》Notebooks 目录 面向中文读者的能运行、可讨论的深度学习教科书 含 PyTorch、NumPy/MXNet、TensorFlow 和 PaddlePaddle 实现 被全球 70 多个国家 500 多所大学用于教学 github 下面是整理好的,可以直接运行的notebook 0 前…...

C#面:简述 .NET Framework 类库中的“命名空间”
在 C# 中,命名空间(Namespace)是一种用于组织和管理代码的机制。它提供了一种将相关的类、接口、结构体和其他类型组织在一起的方式,以便更好地管理和维护代码。 .NET Framework类库中的命名空间是一种逻辑上的分组,它…...
android.os.TransactionTooLargeException解决方案,Kotlin
android.os.TransactionTooLargeException解决方案,Kotlin 首先,特意制造一个让Android发生TransactionTooLargeException的场景,一个Activity启动另外一个Activity,在Intent的Bundle里面塞入一个大的ArrayList: import android.…...
ChatGPT智能聊天系统源码v2.7.6全开源Vue前后端+后端PHP
测试环境:Linux系统CentOS7.6、宝塔、PHP7.4、MySQL5.6,根目录public,伪静态thinkPHP,开启ssl证书 具有文章改写、广告营销文案、编程助手、办公达人、知心好友、家庭助手、出行助手、社交平台内容、视频脚本创作、AI绘画、思维导图等功能 ai通道:文心一言、MiniMax、智…...
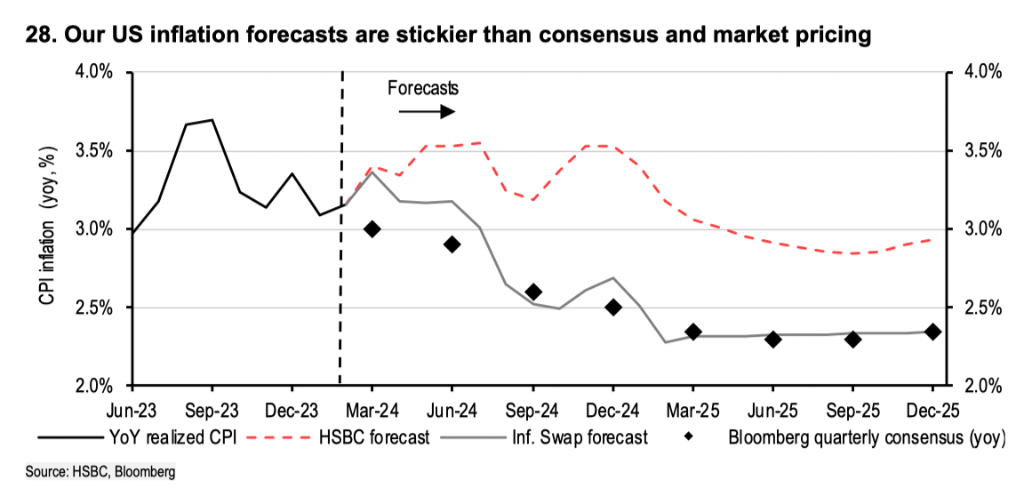
汇丰:当前的美股是泡沫吗?
汇丰认为,当前的风险资产并不构成泡沫,更类似于2017年的市场环境,风险资产有望继续稳步上升。 隔夜美股飙涨,标普创三个月最大周涨,纳指收盘创历史新高。结合去年以来的强劲表现,有观点认为由科技股支撑的…...

颠覆传统:Web3如何塑造未来的数字经济
引言 近年来,随着数字化时代的到来,互联网已经成为人们生活中不可或缺的一部分。然而,随着技术的不断发展和社会的不断变迁,传统的Web2模式逐渐显露出一些弊端,如数据垄断、隐私泄露等问题,这促使人们寻求…...
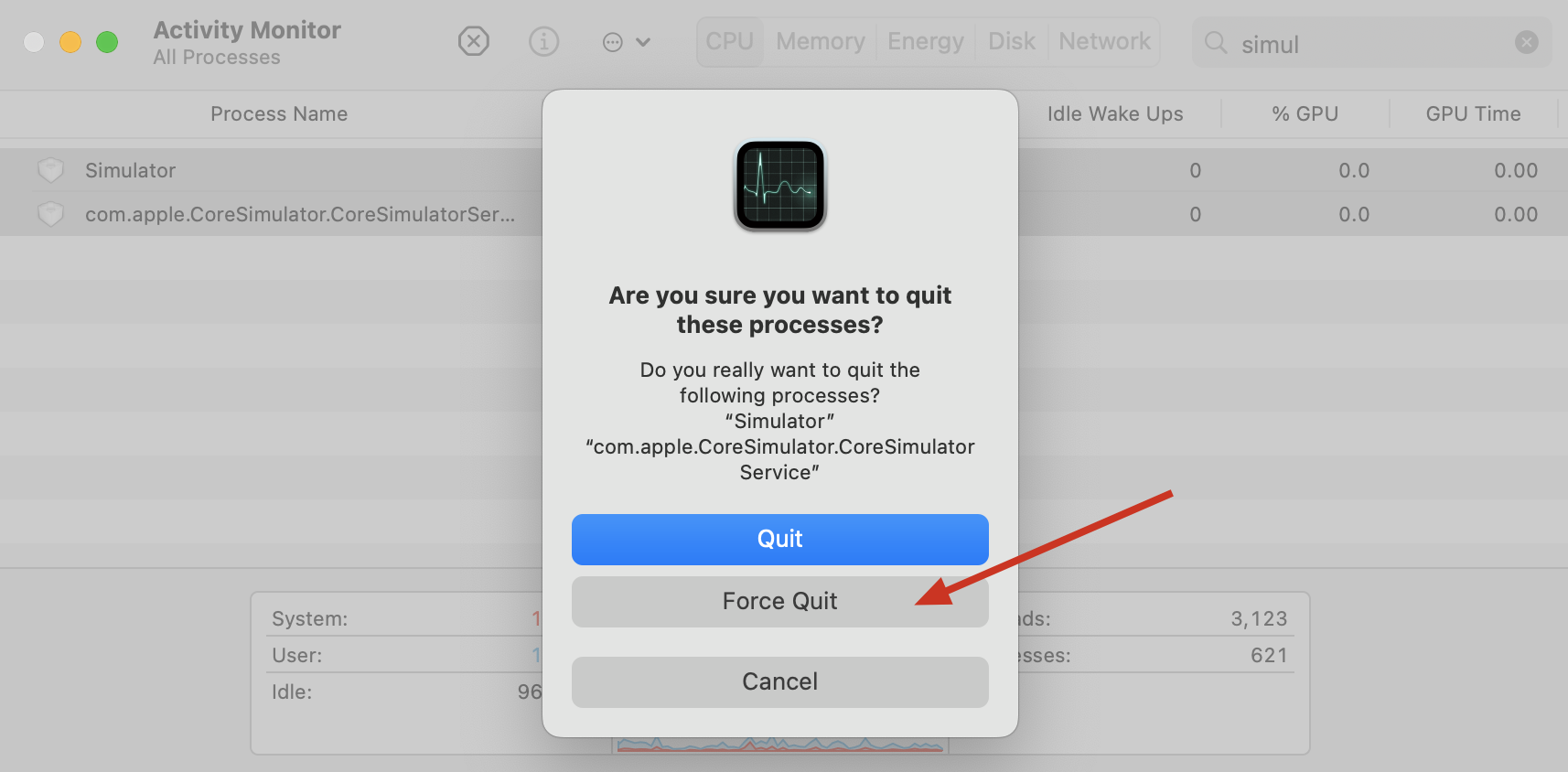
iOS模拟器 Unable to boot the Simulator —— Ficow笔记
本文首发于 Ficow Shen’s Blog,原文地址: iOS模拟器 Unable to boot the Simulator —— Ficow笔记。 内容概览 前言终结模拟器进程命令行改权限清除模拟器缓存总结 前言 iOS模拟器和Xcode一样不靠谱,问题也不少。😂 那就有病治…...

使用 Flink + Faker Connector 生成测试数据压测 MySQL
博主历时三年精心创作的《大数据平台架构与原型实现:数据中台建设实战》一书现已由知名IT图书品牌电子工业出版社博文视点出版发行,点击《重磅推荐:建大数据平台太难了!给我发个工程原型吧!》了解图书详情,…...

Android单片机硬件通信《GPIO通信》
一、什么是GPIO? GPIO(英语:General-purpose input/output),通用型输入输出端口,在单片机上一般是通过一个GND引脚和若干个io引脚配合工作。 单片机可以配置GPIO输入输出模式,与外界环境进行通信交互。在输入环境下&…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...
