蓝桥杯-算法-印章问题
这个题真的顶啊!
思路:
n种图案,m张印章,每一个图案的概率是1/n,这个概率以后用P表示
首先我们定义dp[i][j]是买了i张印章(对应于上面的m),凑齐j种图案的概率(对应于上面的n)
然后是推导:
1.如果i<j的话,说明无论买多少印章,都不能凑齐j种图案,所以概率我们就知道是0,所以二维数组dp[i][j]=0
2.如果j=1,说明买i张印章,凑齐一种的概率
这里分成两种情况讨论。
①如果j=1,说明,买一张凑齐一种的概率,这个概率肯定是1
②如果j>1,说明买j张,凑齐一种的概率是多少。
这里详细点,想一想哈,我们如果买两章,也就是j=2,我们凑齐一种的概率是不是应该这样想:p*p*n。这里的思路是:我们要凑齐一种的概率,但是我们抽了两张,每一张的概率是不是p,两张的概率是不是p*p。但是为什么乘n呢,这样想哈,我们一共有n种印章,每一种的概率是不是都是一样的,所以凑齐的这一个就有可能是n中印章的任意一种。所以得乘一个n
3.接下来是普遍情况了。
我们凑得印章都是随机的,我们买之前是不知道下一个是哪种类别的
所以,如果下一张是之前已经存在过得印章的话(也就是前面买的i-1张已经凑齐了j种,接下来的第i张就是重复前面的印章了),所以这个重复的印章再被抽取的时候,它的概率就是j*p(再详细点,前面已经有了j种了,我们此时假设的是,与之前的重复了,而与每一个重复的概率都是p,所以这里是j*p)
这里的式子是:
dp[i][j] = dp[i-1][j] * (j/n) = dp[i-1][j] *(j*p)
4.然后再就是抽取的印章不是重复的情况了
这个说明前i-1张我们凑齐了j-1种,而第i张,也就是接下来的这一张就是要凑齐的一种,但是我们不确定这一个出现的是没出现印章中的哪一种(有点儿绕,慢慢想一下)。因为前面已经出现了j-1种,所以还有n-(j-1)种没有出现。而接下来的这个只要是这没有出现的一种就行了,这个时候凑齐这一种的概率就是(n-j+1)*p
这里的式子就是:
dp[i][j] = dp[i-1][j-1]*(n-(j-1))/n = dp[i-1][j-1]*(n-j+1)*p
所以对于dp[i][j]这里的情况,就是3,4两种情况相加了。
代码是借鉴的其余博客,未亲自编写
#include<stdio.h>
#include<math.h>
#include<algorithm>
#include<string.h>
#include<iostream>
using namespace std;
double dp[30][30];
int main(void)
{
int n,m;
cin>>n>>m;
double p=1.0/n;
memset(dp,0,sizeof(dp));
for(int i=1;i<=m;i++)//i张印章
{
for(int j=1;j<=n;j++)//j种图案
{
if(i<j)//不可能凑齐
{
dp[i][j]=0;
}
if(j==1)//j只要所有图案中的一种就可以了,所以我们(1/n)^i还要再乘n,就是p^i-1
{
dp[i][j]=pow(p,i-1);
}
else//买了i张凑齐j种,第i张 要么和之前凑齐的一样,要么不一样
{
dp[i][j]=dp[i-1][j]*(j*p)+dp[i-1][j-1]*(n-j+1)*p;
}} }
printf("%.4lf\n",dp[m][n]);
return 0;
} 相关文章:

蓝桥杯-算法-印章问题
这个题真的顶啊!思路:n种图案,m张印章,每一个图案的概率是1/n,这个概率以后用P表示首先我们定义dp[i][j]是买了i张印章(对应于上面的m),凑齐j种图案的概率(对应于上面的n…...

戴尔游匣G16电脑U盘安装系统操作教程分享
戴尔游匣G16电脑U盘安装系统操作教程分享。有用户在使用戴尔游匣G16电脑的时候遇到了系统问题,比如电脑蓝屏、自动关机重启、驱动不兼容等问题。遇到这些问题如果无法进行彻底解决,我们可以通过U盘重新安装系统的方法来解决,因为这些问题一般…...

2023数学建模美赛赛题思路分析 2023美赛 美国大学生数学建模数模
将在本帖更新2023美国大学生数学建模数模美赛各个赛题思路,大家可以点赞收藏! 一、参赛报名 组队参赛(每队人数3人,专业不限)。 二、赛题思路及资料 会在本帖更新思路分析,Q群可领取模型代码/赛题思路资料…...

vue3与vue2的对比
Vue 3.0 和 Vue 2.0 是 Vue 前端框架的两个主要版本,它们有着不同的更新和优化: Vue 3.0 主要更新内容: 采用 TypeScript 作为开发语言,提高了代码的类型安全性。 速度更快,内存使用更少,支持大规模数据处…...
备战金三银四)
史上最全软件测试工程师常见的面试题总结(百度、oppo、中软国际、华为)备战金三银四
1、面试:神州数码1.介绍你下你项目中一个自动化实现的流程2.你觉得做自动化的意义在哪里 >需要对之前已经实现的功能进行回归测试、保证当前版本更新的内容不能影响到之前已经实现好的功能3.你们做自动化产生了什么结果 >测试报告、报错截图和报错日志、测试报…...
“深度学习”学习日记。卷积神经网络--用CNN的实现MINIST识别任务
2023.2.11 通过已经实现的卷积层和池化层,搭建CNN去实现MNIST数据集的识别任务; 一,简单CNN的网络构成: 代码需要在有网络的情况下运行,因为会下载MINIST数据集,运行后会生成params.pkl保留训练权重&…...

JavaWeb--JDBC练习
JDBC练习5.1 需求5.2 案例实现5.2.1 环境准备5.2.2 查询所有5.2.3 添加数据5.2.4 修改数据5.2.5 删除数据5.1 需求 完成商品品牌数据的增删改查操作 查询:查询所有数据添加:添加品牌修改:根据id修改删除:根据id删除 5.2 案例实…...

【LeetCode】2335. 装满杯子需要的最短总时长
2335. 装满杯子需要的最短总时长 题目描述 现有一台饮水机,可以制备冷水、温水和热水。每秒钟,可以装满 2 杯 不同 类型的水或者 1 杯任意类型的水。 给你一个下标从 0 开始、长度为 3 的整数数组 amount ,其中 amount[0]、amount[1] 和 a…...

Android 12.0 通过驱动实现禁用usb鼠标和usb键盘功能
1.1概述 在12.0的系统产品定制化开发中,在进行定制中有关于usb键盘和usb鼠标的需求中,产品要求禁止usb口挂载usb鼠标和usb键盘,所以需要要求在usb挂载类型的时候 判断如果是usb鼠标和usb键盘就不让挂载,这就需要从驱动方面入手来解决这个问题,接下来看下驱动的某些挂载usb…...
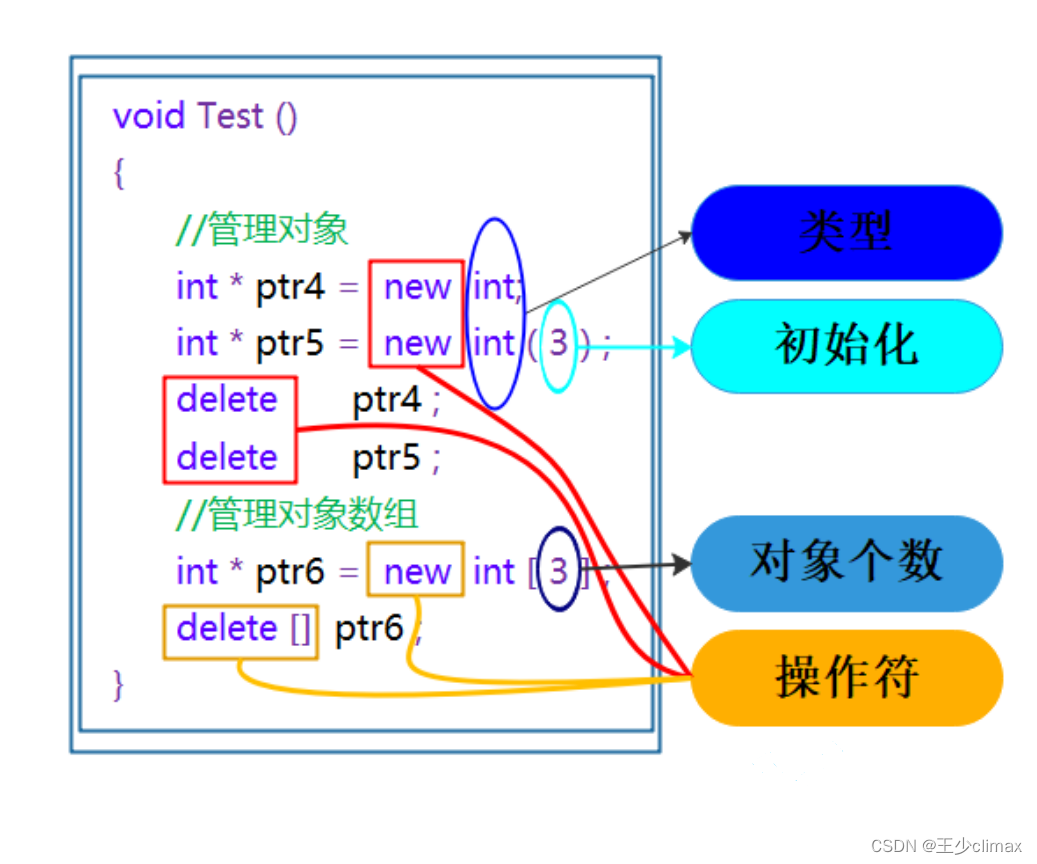
C++入门——内存管理
C入门——内存管理 C/C内存分布 分类是为了更好的管理 int globalVar 1; static int staticGlobalVar 1; void Test() {static int staticVar 1;int localVar 1;int num1[10] {1, 2, 3, 4};char char2[] "abcd";char* pChar3 "abcd";int* ptr1 (…...
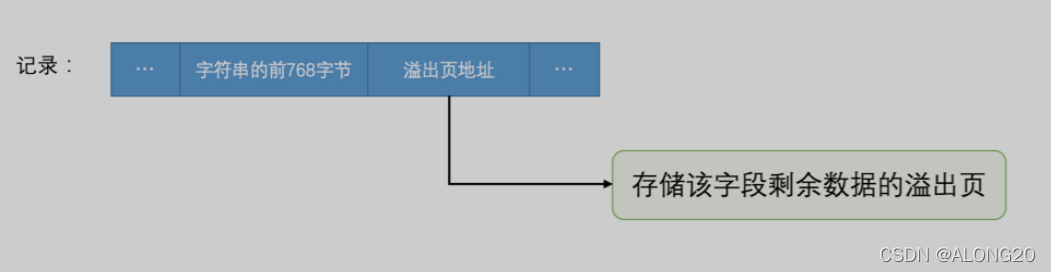
MySQL-InnoDB行格式浅析
简介 我们知道读写磁盘的速度非常慢,和内存读写差了几个数量级,所以当我们想从表中获取某些记录时, InnoDB 存储引擎需要一条一条的把记录从磁盘上读出来么? 不,那样会慢死,InnoDB 采取的方式是:…...
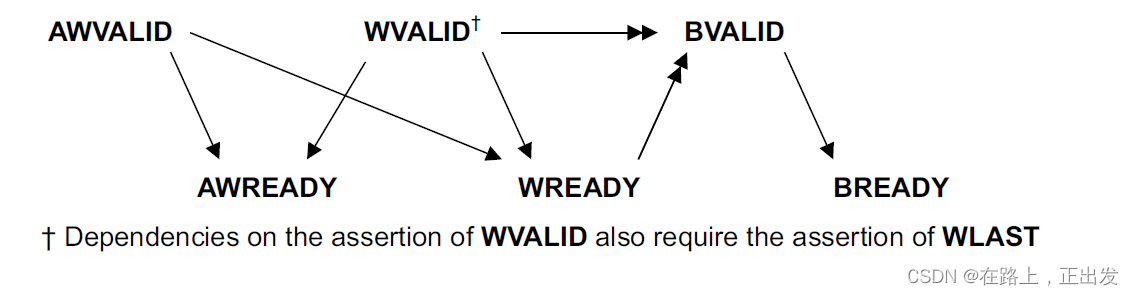
AXI 总线协议学习笔记(4)
引言 前面两篇博文从简单介绍的角度说明了 AXI协议规范。 AXI 总线协议学习笔记(2) AXI 总线协议学习笔记(3) 从本篇开始,详细翻译并学习AXI协议的官方发布规范。 文档中的时序图说明: AXI指࿱…...

C++复习笔记6
1.String类的实现 注意深浅拷贝, C语言字符串拼接函数strcat() #define _CRT_SECURE_NO_WARNINGS #include<iostream> #include<vld.h> #include<assert.h> using namespace std;class String {friend ostream& operator<<(ostream &am…...
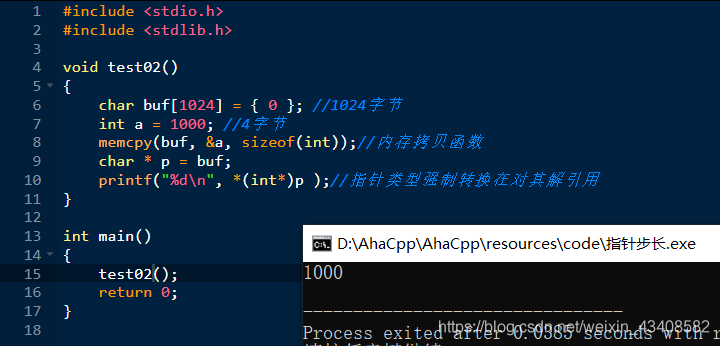
指针的步长及意义(C语言基础)
指针的步长及意义 文章目录指针的步长及意义指针变量1后偏移的字节数不同指针解引用时取出的字节数不同其他例子不同类型的指针有何不同的意义指针变量1后跳跃字节数量不同解引用的时候,取出字节数量不同 指针变量1后偏移的字节数不同 代码演示:&#…...
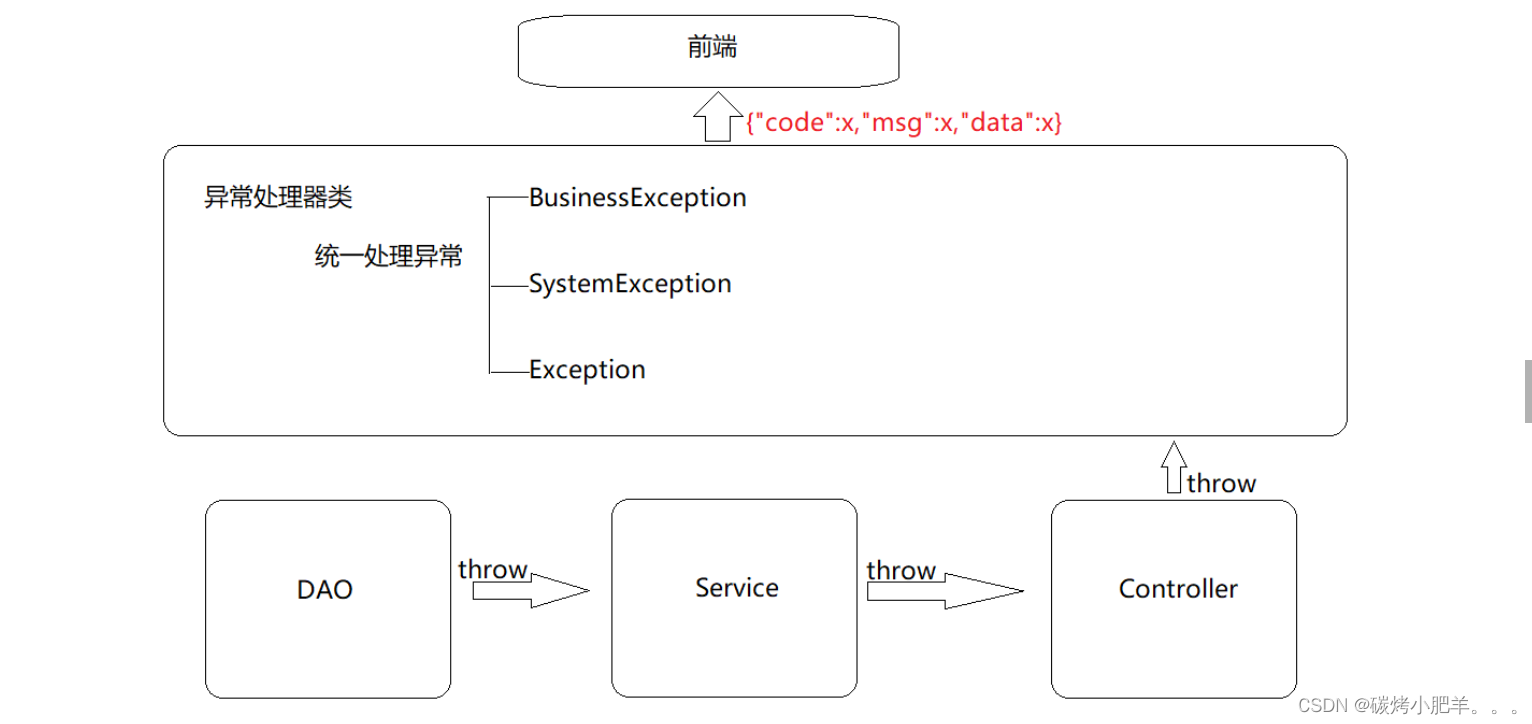
SpringMVC:统一异常处理(11)
统一异常处理1. 说明2. 问题描述3. 异常处理器使用3.1 创建异常处理器类3.2 让程序抛出异常3.3 测试4. 项目异常处理方案4.1 异常分类4.2 异常解决方案4.3 异常解决方案的具体实现4.4 测试5. 总结1. 说明 \quad本篇文章是在文章SpringMVC:SSM整合(Spring…...
SpringBoot的配置与使用
SpringBoot简介 我们的Spring是包含了众多工具的IoC容器,而SpringBoot则是Spring的加强版,可以更加方便快捷的使用 如果Spring是手动挡的车,那么SpringBoot就是自动挡的车,让我们的驾驶体验变得更好 SpringBoot具有一下几种特征…...
【Python】tkinter messagebox练习笔记
我一好友在朋友圈看到人家用代码花式秀恩爱,让我也做一个,我就用我学习半年python的功力,做了这一个东西。🙏窗口主页面(图一)为了让我这个盆友有颜面,特意做了一个问答问他帅不帅,以…...
答案解析)
2022年12月电子学会Python等级考试试卷(五级)答案解析
青少年软件编程(Python)等级考试试卷(五级) 分数:100 题数:38 一、单选题(共25题,共50分) 1. 下面哪个语句正确定义了元组类型数据tuple1?( ) A. t…...
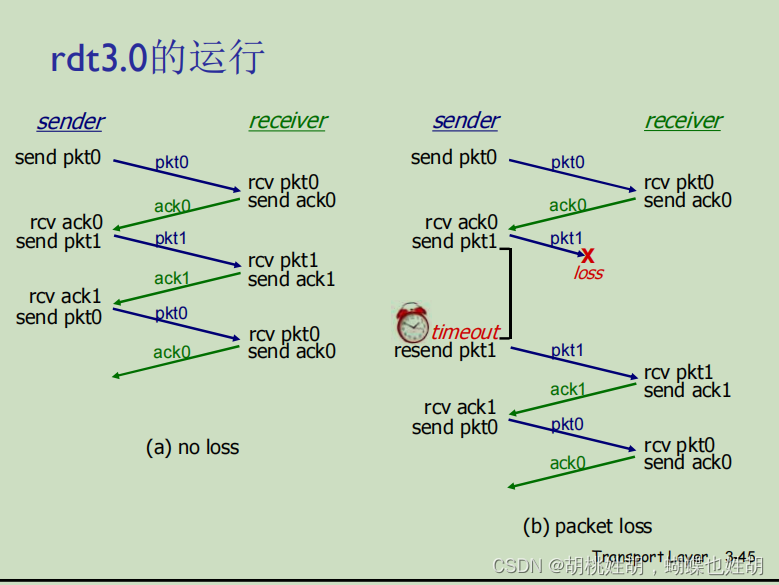
计算机网络自定向下 -- 浅谈可靠性之rdt协议
可靠性数据传输原理 可靠指数据在传输过程中不错,不丢,不乱 运输层要为应用层提供一种服务:数据可以通过一条可靠的信道进行传输,在该信道中传输的数据不会受到损坏或者丢失, 实现这种服务的是可靠数据传输协议。 要实现这种服…...
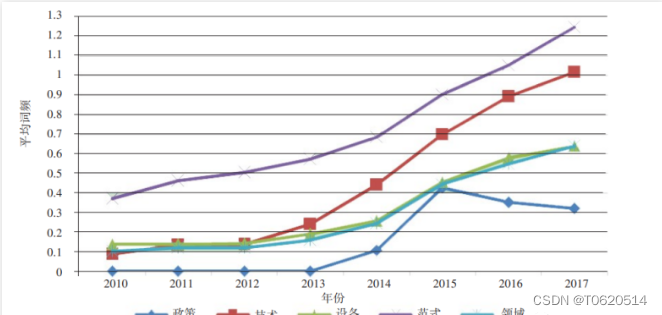
制造业升级转型:制造业上市公司-智能制造词频统计数据集
发展智能制造,关乎中国制造业转型升级的成效。基于中国制造业上市公司年报,通过文本数据挖掘,提取关键词反映企业对智能制造的关切焦点,进而运用词频及共词网络分析,洞察中国智能制造的发展态势。 研究发现࿰…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...
