【力扣1653】使字符串平衡的最少删除次数
给你一个字符串 s ,它仅包含字符 'a' 和 'b' 。
你可以删除 s 中任意数目的字符,使得 s 平衡 。当不存在下标对 (i,j) 满足 i < j ,且 s[i] = 'b' 的同时 s[j]= 'a' ,此时认为 s 是 平衡 的。
请你返回使 s 平衡 的 最少 删除次数。
示例 1:
输入:s = "aababbab"
输出:2
解释:你可以选择以下任意一种方案:
下标从 0 开始,删除第 2 和第 6 个字符("aababbab" -> "aaabbb"),
下标从 0 开始,删除第 3 和第 6 个字符("aababbab" -> "aabbbb")。
示例 2:
输入:s = "bbaaaaabb"
输出:2
解释:唯一的最优解是删除最前面两个字符。
提示:
1 <= s.length <= 105
s[i] 要么是 'a' 要么是 'b' 。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/minimum-deletions-to-make-string-balanced
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
我觉得这是一道挺典型的前缀和的题目,但是是假前缀和->如果你想节省空间的话,不用全记。
首先思考人类是怎么做这道题的。
枚举吗?枚举什么?
前a后b,枚举的是断点。
假设我们确定了断点是i这个位置,假设[0,i-1]是a,[i,end]是b,怎么计算要删除多少?
=>[0,i-1]中b的个数+[i,end]中a的个数。
那每次统计i点需要删除多少的时候需要重新统计a和b的个数吗?不需要,只需要根据当前的数决定谁加谁减就可以了。
b是正序前缀和,a是逆序前缀和。
class Solution {
public:int minimumDeletions(string s) {int l=s.length();if(l==1){return 0;}int conta=0;int contb=0;if(s[l-1]=='a'){conta=1;}if(s[0]=='b'){contb=1;}for(int i=l-2;i>=0;--i){if(s[i]=='a'){conta++;} }int cont=conta;if(s[0]=='a'){conta--;}for(int i=1;i<l;++i){cont=min(cont,conta+contb);if(s[i]=='b'){contb++;}else{conta--;}}cont=min(cont,contb);return cont;}
};但是感觉两次循环还是得有的,毕竟方向不一样。
动态规划的方法是我最开始的思路,但是我想不通也写不出来,现在还没看懂,谁给我仔细讲讲。。。
相关文章:

【力扣1653】使字符串平衡的最少删除次数
给你一个字符串 s ,它仅包含字符 a 和 b 。你可以删除 s 中任意数目的字符,使得 s 平衡 。当不存在下标对 (i,j) 满足 i < j ,且 s[i] b 的同时 s[j] a ,此时认为 s 是 平衡 的。请你返回使 s 平衡 的 最少 删除次数。…...
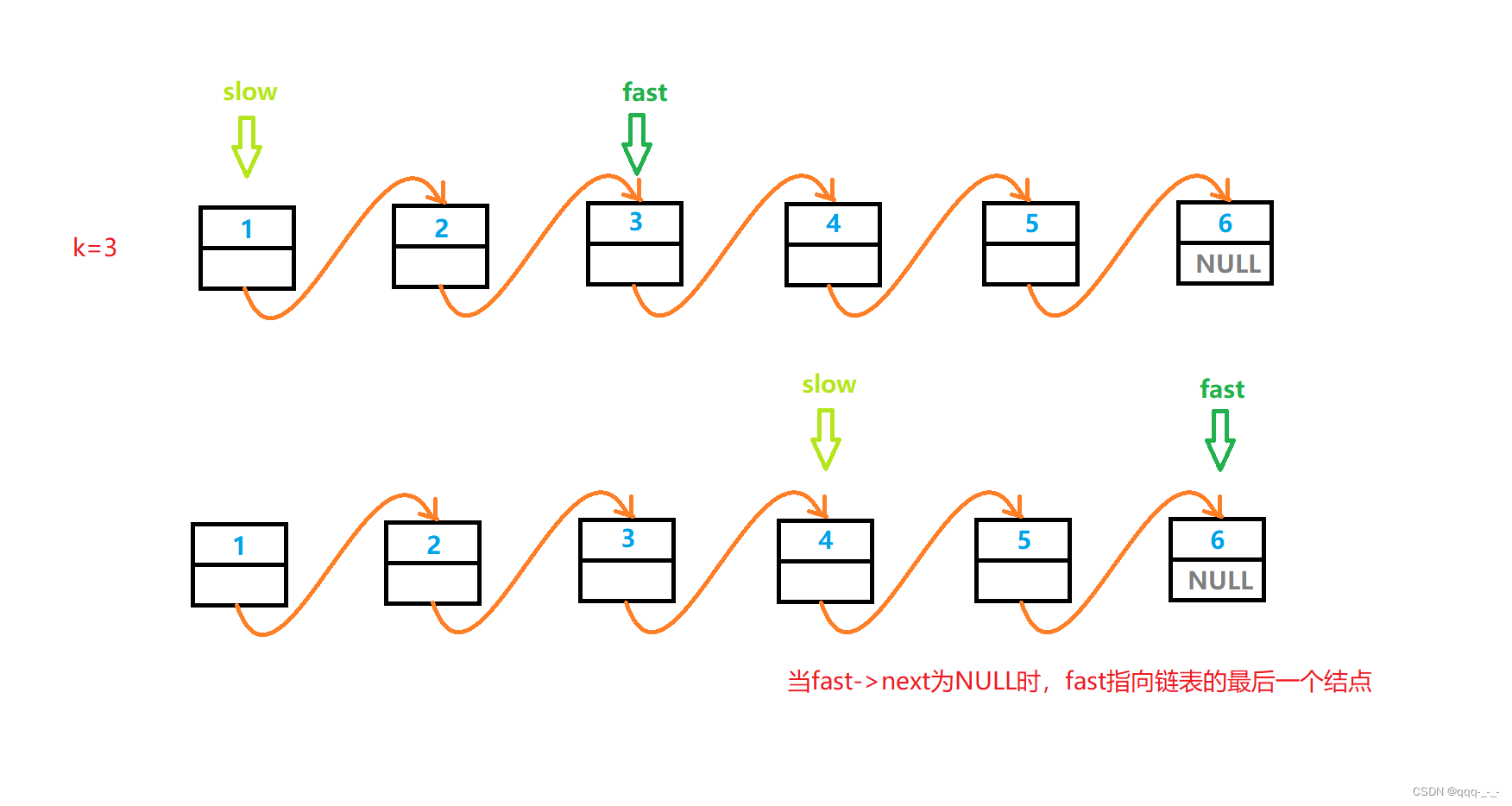
链表的中间结点与链表的倒数第k个结点(精美图示详解哦)
全文目录引言链表的中间结点题目描述与思路实现链表的倒数第k个结点题目描述与思路实现总结引言 在上一篇文章中,介绍了反转链表 我们利用了链表是逻辑连续的特点,逆置了链表的逻辑连接顺序,从而实现反转链表: 戳我查看反转链表详…...
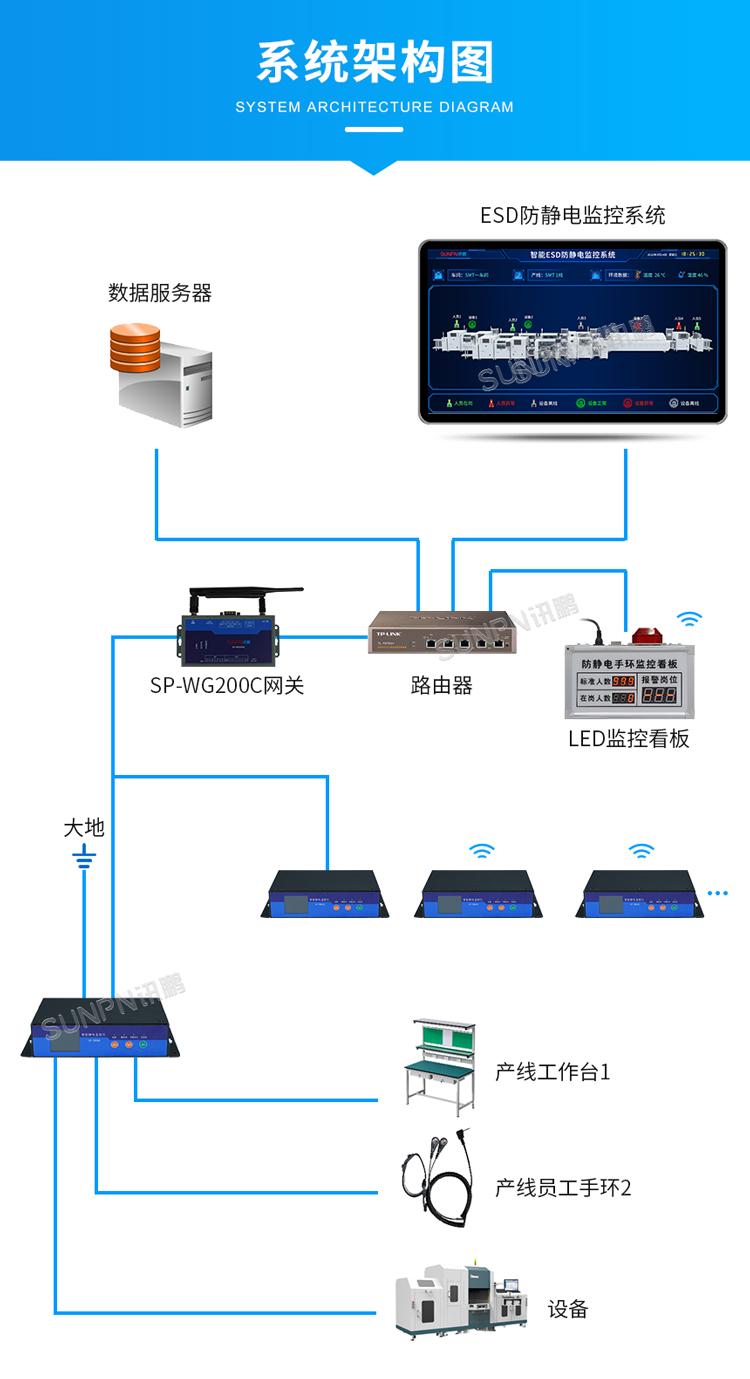
防静电监控仪可以检测现场设备是否和实际大地接触
随着电子产品集成化度越来越高,对于电子产品装配来说,静电的危害严重影响到产品的质量、成品率和可靠性, 必须对用于电子产品装配的净化间进行系统防静电措施,将生产过程中的静电危害程度降至最低。近年来电子企业对ESD的危害的深入认识&…...

计算机网络第八版——第二章课后题答案(超详细)
第二章 该答案为博主在网络上整理,排版不易,希望大家多多点赞支持。后续将会持续更新(可以给博主点个关注~ 第一章 答案 【2-01】物理层要解决哪些问题?物理层的主要特点是什么? 解答:物理层考虑的是怎…...

2023年3月全国DAMA-CDGA/CDGP数据管理认证火热报名中...
弘博创新是DAMA中国授权的数据治理人才培养基地,贴合市场需求定制教学体系,采用行业资深名师授课,理论与实践案例相结合,快速全面提升个人/企业数据治理专业知识与实践经验,通过考试还能获得数据专业领域证书。 DAMA认…...
相关信息)
查询与进程调度(CFS)相关信息
目录 查询与进程相关的调度信息 查看CFS调度信息 CPU相关的信息 CFS就绪队列的总运行时间 实时队列与deadline调度的相关信息 所有进程相关的信息 查询与进程相关的调度信息 进程的nice值,优先级,调度策略,vruntime等信息。在proc目录下…...

07对MVC的理解
MVC是一种设计模式,用于将应用程序的不同方面分离开来,以便更容易地管理和维护应用程序。MVC代表模型-视图-控制器,它将应用程序分为三个主要组件:模型(Model):负责管理应用程序的数据和业务逻辑…...

WebSocket与Socket、TCP、HTTP的关系
目录:1、名词解析;2、WebSocket简介与原理;3、WebSocket和Http的关系和异同点;4、WebSocket与Socket的区别;5、Socket和TCP/IP;6、一个应用程序的通信链路;1、基础名词解析:…...
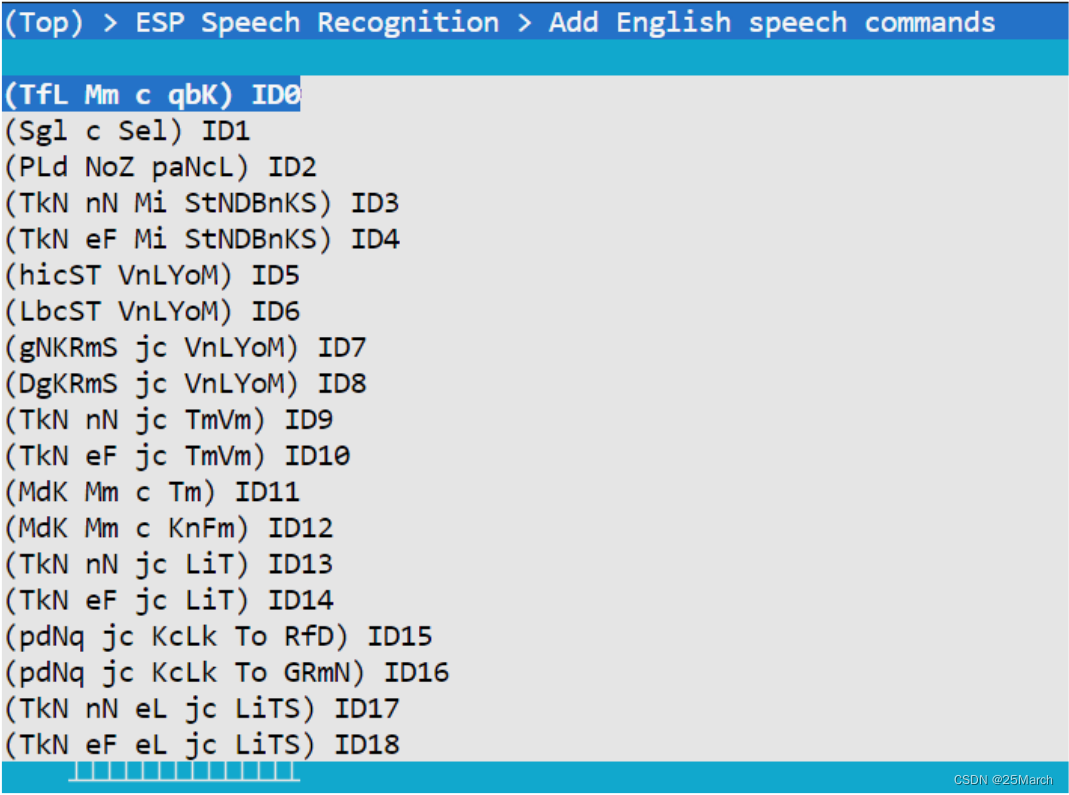
音频基础知识简述 esp-sr 上手指南
此篇博客先对音频基础知识进行简要叙述,然后帮助读者入门 esp-sr SDK。 1 音频的基本概念 1.1 声音的本质 声音的本质是波在介质中的传播现象,声波的本质是一种波,是一种物理量。 两者不一样,声音是一种抽象的,是声…...

Flex弹性布局一文通【最全Flex教学】
文章目录一.Flex布局1.1 传统布局和flex布局1.1.1 传统布局1.1.2 flex弹性布局1.2 flex初步体验1.3 布局原理二.常见Flex属性2.1 常见父项属性2.2 flex-direction主轴的方向2.3 justify-content设置主轴上的子元素排列方式2.4 设置子元素是否flex-wrap换行2.5 align-itmes设置侧…...
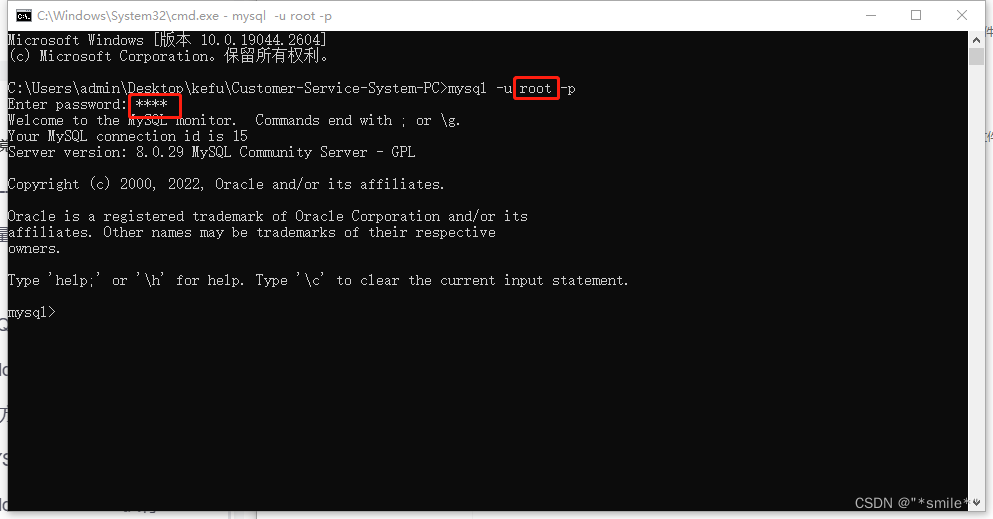
Navicat使用教程
Navicat:一个可以对别人的数据库进行操作的软件(需要与如mysql等数据库配套使用) 1. 下载mysql MySQL :: Download MySQL Community Server (Archived Versions) 下载上面那个版本 下载下来是个压缩包,解压 2.配置mysql (1)在…...

35岁测试人该何去何从?10年工作经验的我,只不过是一年的工作经验用了10年......
如果到了这个年龄,还是初级测试,或者只会一些简单的自动化测试,那么真的是不好干了。 35的年龄,企业对员工是有另一层面的考量。 简单来说,就是年龄上去了,能力也要上去,要么是技术专家&#…...
SpringBoot 项目中集成 Prometheus 和 Grafana
项目上线后,除了能保障正常运行以外,也需要服务运行的各个指标进行监控,例如 服务器CPU、内存使用占比,Full GC 执行时间等,针对一些指标出现异常,可以加入一些报警机制能及时反馈给开发运维。这样…...

红队APT——反朔源流量加密CSMSF证书指纹C2项目CDN域前置
目录 0x01 背景交代 0x02 常见红蓝对抗中红队面临问题 0x03 蓝队发现处置情况...
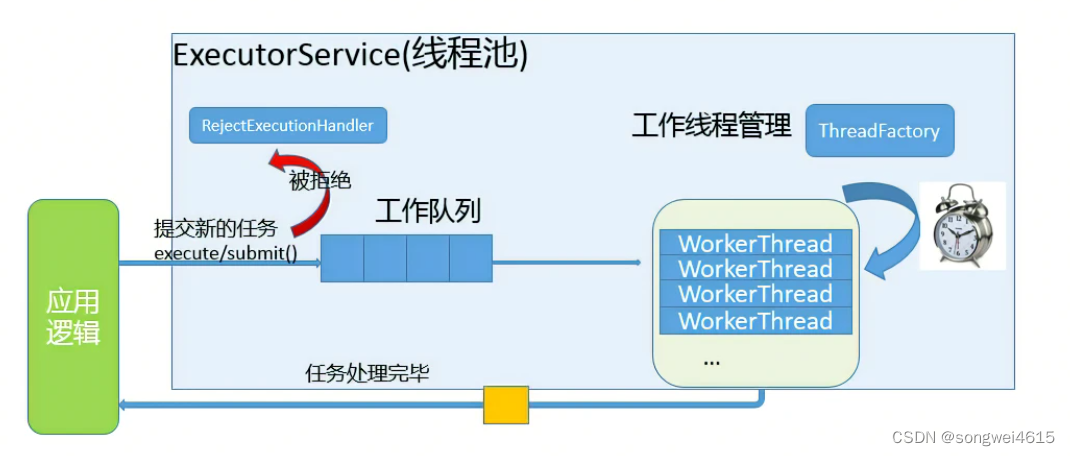
Linux环境下实现并详细分析c/cpp线程池(附源码)
一、线程池原理 如果并发的线程数量很多,并且每个线程都是执行一个时间很短的任务就结束了,这样频繁创建线程就会大大降低系统的效率,因为频繁创建线程和销毁线程需要时间。 线程池是一种多线程处理形式,处理过程中将任务添加到…...

移动web(三)
her~~llo,我是你们的好朋友Lyle,是名梦想成为计算机大佬的男人! 博客是为了记录自我的学习历程,加强记忆方便复习,如有不足之处还望多多包涵!非常欢迎大家的批评指正。 媒体查询 目标:能够根据…...

macbook怎么运行exe文件 mac打开exe文件的三大方法
exe文件是Windows系统的可执行文件,虽然Mac系统上无法直接打开exe文件,但是你可以在Mac电脑上安装双系统或者虚拟机来实现mac电脑上运行exe文件。除了这两种方法之外,你还可以在Mac电脑上使用类虚拟机软件打开exe文件,这三种方法各…...
高可用XAG部署)
GoldenGate(OGG)高可用XAG部署
前言: 本文档主要描述通过Oracle Grid Infrastructure Agents (XAG)基于Oracle RAC实现GoldenGate(OGG)软件高可用的实施操作 环境信息: 源端 目标端 节点一IP 节点二IP 192.168.1.84 192.168.1.86 节点一IP 节点二IP 192.168.1.200 192.168.1.210 VIP 192.…...

如何使用Docker容器部署O2OA(翱途)开发平台与OnlyOffice的集成版本?
O2OA(翱途)开发平台[下称O2OA平台或者O2OA]默认可以和OnlyOffice进行集成来实现在线文档编辑以及流程集成。开发者可以直接安装O2OA官网的OnlyOfficeO2Server的Docker版本用于体验。本文将详细介绍如何安装O2OA OnlyOffice的Docker版本。OnlyOffice Docs Sever可以单独安装,O2…...
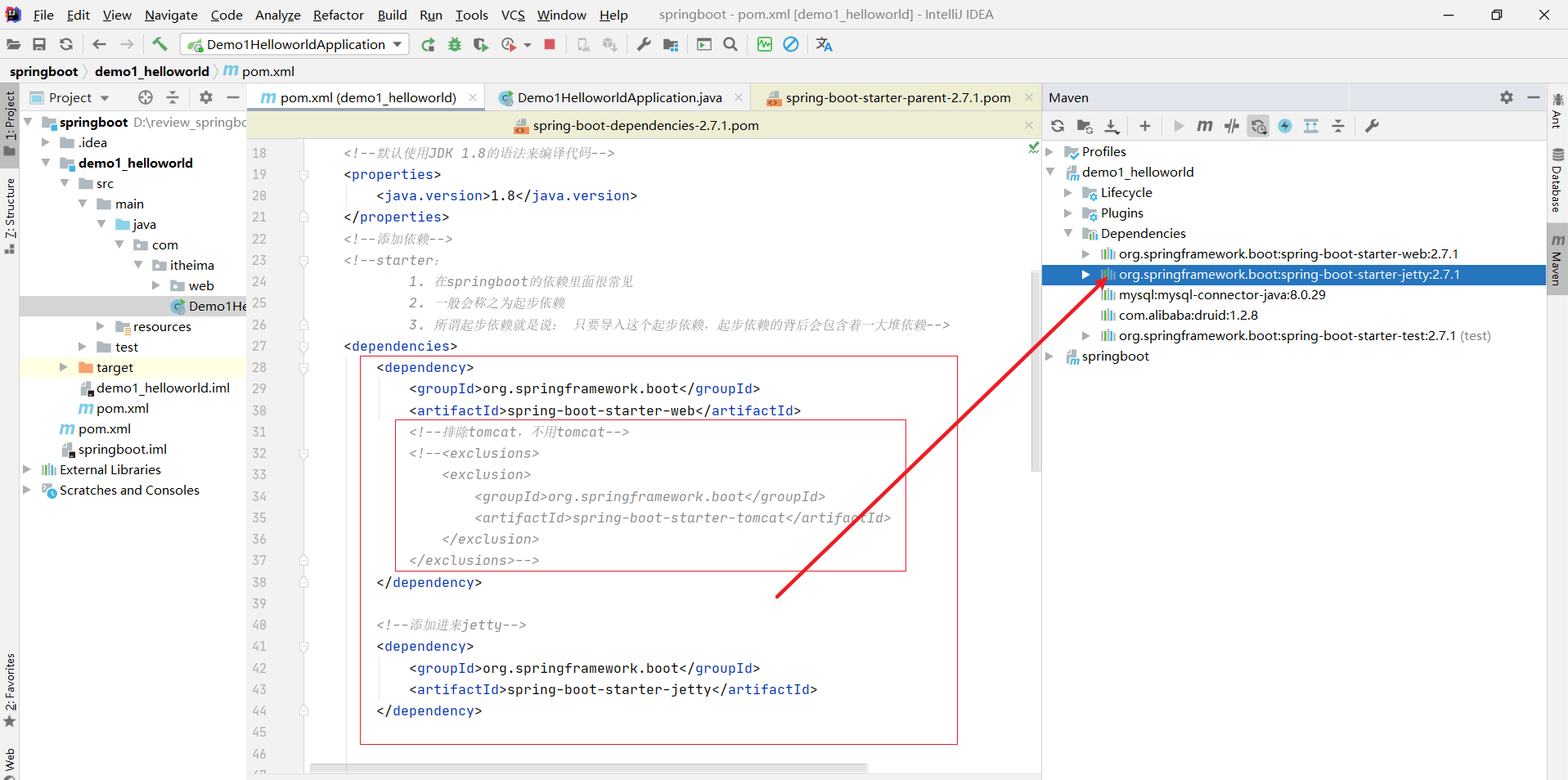
springboot复习(黑马)(持续更新)
学习目标基于SpringBoot框架的程序开发步骤熟练使用SpringBoot配置信息修改服务器配置基于SpringBoot的完成SSM整合项目开发一、SpringBoot简介1. 入门案例问题导入SpringMVC的HelloWord程序大家还记得吗?SpringBoot是由Pivotal团队提供的全新框架,其设计…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
