算法-最短路径
图的最短路径问题是一个经典的计算机科学和运筹学问题,旨在找到图中两个顶点之间的最短路径。这种问题在多种场景中都有应用,如网络路由、地图导航等。
解决图的最短路径问题有多种算法,其中最著名的包括:
1.迪杰斯特拉算法
(1). 图的要求
适用于权重非负的图。
(2). 实现
该算法的实现通常包括以下步骤:
a. 初始化:将源节点标记为最短路径已经知道.设置其路径距离为0.将其入队列.
b. 循环迭代,直到队列为空
b.1. 出队列,得p.
b.2.迭代&更新.
即对从p可达,且最短路径尚未确定节点q.
比较,若p的路径距离+Edge<p,q>小于q的路径距离,则更新q的路径距离=p的路径距离+Edge<p,q>.设置p为其路径上一节点.
b.3.从最短路径尚未确定节点中选出路径值最小节点t.将t的最短路径标记为已经知道.t入队列.在无法选出这样的t时,表示剩余节点均不可达.可提前结束迭代.
(3). 实例
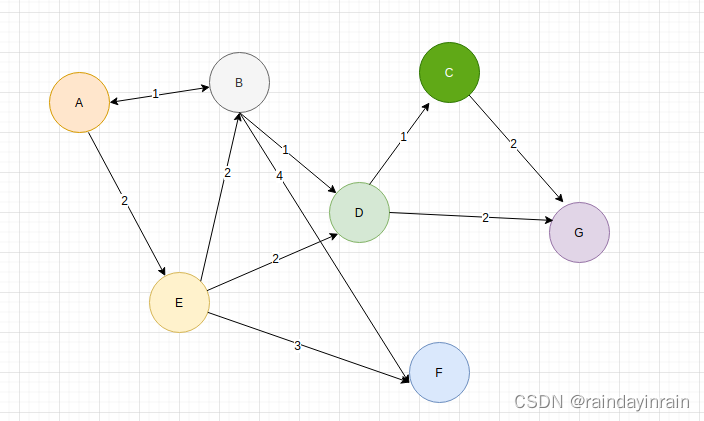
(4). 算法实现
#define MAX 0x7fffffff
class NodeInfo{
public:char m_nName;int32_t m_nPath = MAX;int32_t m_nPreIndex = -1;int32_t m_nTag = -1;
};template<class T>
class Node{
public:T m_nEle;
};template<class EdgeInfo>
class Edge{
public:int32_t m_nWeight = MAX;bool m_bValid = false;
};Node<NodeInfo> stNodes[7];
Edge<int> stEdges[7][7];
void Sort(void* lpBegin, void *lpEnd);
int main(){stNodes[0].m_nEle.m_nName = 'A';stNodes[1].m_nEle.m_nName = 'B';stNodes[2].m_nEle.m_nName = 'C';stNodes[3].m_nEle.m_nName = 'D';stNodes[4].m_nEle.m_nName = 'E';stNodes[5].m_nEle.m_nName = 'F';stNodes[6].m_nEle.m_nName = 'G';stEdges[0][1].m_nWeight = 1;stEdges[0][1].m_bValid = true;stEdges[1][0].m_bValid = true;stEdges[1][0].m_nWeight = 1;stEdges[0][4].m_bValid = true;stEdges[0][4].m_nWeight = 2;stEdges[4][1].m_bValid = true;stEdges[4][1].m_nWeight = 2;stEdges[1][3].m_bValid = true;stEdges[1][3].m_nWeight = 1;stEdges[1][5].m_bValid = true;stEdges[1][5].m_nWeight = 4;stEdges[4][3].m_bValid = true;stEdges[4][3].m_nWeight = 2;stEdges[3][2].m_bValid = true;stEdges[3][2].m_nWeight = 1;stEdges[3][6].m_bValid = true;stEdges[3][6].m_nWeight = 2;stEdges[2][6].m_bValid = true;stEdges[2][6].m_nWeight = 2;int nSourceIndex = 0;stNodes[nSourceIndex].m_nEle.m_nTag = 1;stNodes[nSourceIndex].m_nEle.m_nPath = 0;stNodes[nSourceIndex].m_nEle.m_nPreIndex = -1;int32_t nArrQueue[7];int32_t nFirst = 0;int32_t nEnd = 0;int32_t nNum = 0;nArrQueue[0] = nSourceIndex;nFirst = 0;nEnd = 1;nNum = 1;while(nNum > 0){// 出队列int32_t nIndex;if(nNum = 1){nIndex = nArrQueue[nFirst];nFirst = 0;nEnd = 0;nNum = 0;}else{nIndex = nArrQueue[nFirst];nFirst = (nFirst+1)%7;nNum--;}// 迭代&更新for(int32_t i = 0; i < 7; i++){if(stEdges[nIndex][i].m_bValid && stNodes[i].m_nEle.m_nTag == -1){if(stNodes[i].m_nEle.m_nPath > stNodes[nIndex].m_nEle.m_nPath + stEdges[nIndex][i].m_nWeight){stNodes[i].m_nEle.m_nPath = stNodes[nIndex].m_nEle.m_nPath + stEdges[nIndex][i].m_nWeight;stNodes[i].m_nEle.m_nPreIndex = nIndex;}}}// 入队列// 选择未访问节点中最短距离最小的一个nIndex = -1;int32_t nMin = MAX;for(int32_t i = 0; i < 7; i++){if(stNodes[i].m_nEle.m_nTag == -1 && stNodes[i].m_nEle.m_nPath < nMin){nMin = stNodes[i].m_nEle.m_nPath;nIndex = i;}}if(nIndex == -1){break;// 所有节点均已被访问.或剩余节点全部不可达.}// 选举的节点就是最短路径已知的stNodes[nIndex].m_nEle.m_nTag = 1;if(nNum == 0){nArrQueue[0] = nIndex;nFirst = 0;nEnd = 1;nNum++;}else{nArrQueue[nEnd] = nIndex;nEnd = (nEnd+1)%7;nNum++;}}// testprintf("finish\n");while(true){int32_t nIndex = -1;scanf("%d", &nIndex);getchar();printf("path_%d\n", stNodes[nIndex].m_nEle.m_nPath);printf("%c ", stNodes[nIndex].m_nEle.m_nName);while(nIndex != -1){printf("%c ", stNodes[stNodes[nIndex].m_nEle.m_nPreIndex].m_nEle.m_nName);nIndex = stNodes[nIndex].m_nEle.m_nPreIndex;}printf("\n");}return 0;
}
2.贝尔曼-福特算法(Bellman-Ford Algorithm):
(1). 图的要求
可以处理带有负权重的图,但无法处理包含负权重环的图。
针对权重为负的图,可以让所有边权中加上一个基础量转变为权重非负的,再通过迪杰斯特拉求解.所以,正常没必要用这个.
时间复杂度为O(|V|*|E|)。
(2). 算法
贝尔曼-福特算法(Bellman-Ford Algorithm)的实现过程可以分为以下三个阶段:
a. 初始化阶段:
创建一个数组Distant,用于记录从源点s到图中各个顶点的最短路径长度估计值。通常,将源点s到自己的距离Distant[s]初始化为0,而将源点s到其他所有顶点的距离初始化为一个较大的值(如无穷大),表示这些顶点与源点之间的最短路径尚未确定。
b. 松弛操作阶段:
这个阶段需要进行|V|-1次迭代,其中V是图中顶点的数量。在每一次迭代中,遍历图中的所有边(u, v),并检查是否可以通过这条边来更新从源点s到顶点v的最短路径长度估计值。
具体来说,对于每一条边(u, v),如果Distant[u] + w(u, v) < Distant[v],则更新Distant[v]为Distant[u] + w(u, v)。这里,w(u, v)是边(u, v)的权重,表示从顶点u到顶点v的距离或成本。
通过不断的松弛操作,Distant数组中的值会逐渐逼近从源点到各个顶点的实际最短路径长度。
c. 负权回路检测阶段:
在完成|V|-1次松弛操作后,再进行一次额外的松弛操作。这次操作的目的是为了检测图中是否存在负权回路(即从某个顶点出发,经过一系列边后回到该顶点,且整个回路的总权重为负)。
如果在额外的松弛操作中,仍然有Distant数组的值被更新,那么就说明图中存在负权回路。因为负权回路的存在会导致最短路径问题无解,因为可以通过不断绕行负权回路来减小路径长度。
如果额外的松弛操作没有更新Distant数组的值,那么算法结束,Distant数组中存储的就是从源点到各个顶点的最短路径长度。
相关文章:

算法-最短路径
图的最短路径问题是一个经典的计算机科学和运筹学问题,旨在找到图中两个顶点之间的最短路径。这种问题在多种场景中都有应用,如网络路由、地图导航等。 解决图的最短路径问题有多种算法,其中最著名的包括: 1.迪杰斯特拉算法 (1).…...
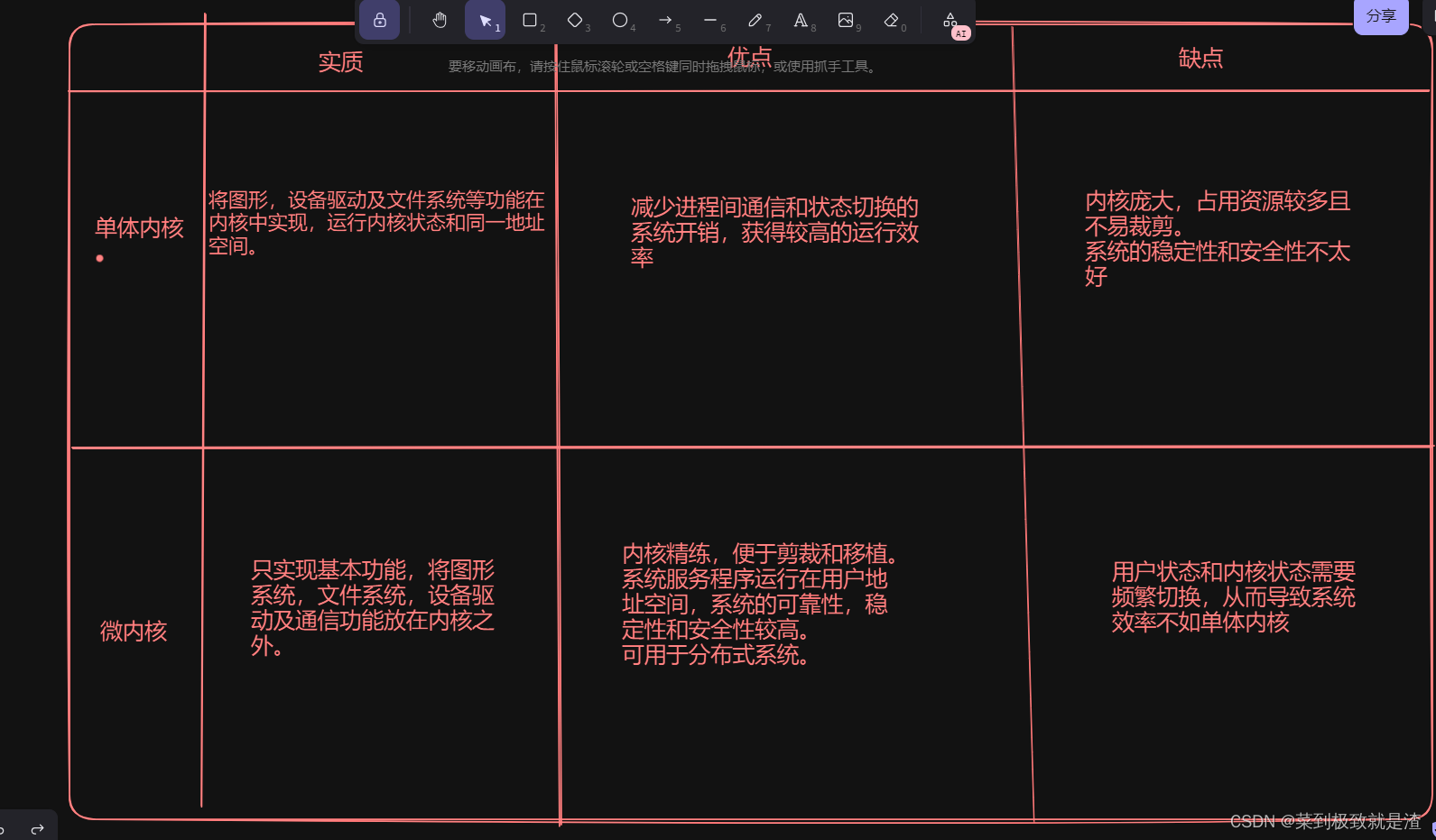
【软考---系统架构设计师】特殊的操作系统介绍
目录 一、嵌入式系统(EOS) (1)嵌入式系统的特点 (2)硬件抽象层 (3)嵌入式系统的开发设计 二、实时操作系统(RTOS) (1)实时性能…...
)
大模型: 提示词工程(prompt engineering)
文章目录 一、什么是提示词工程二、提示词应用1、提示技巧一:表达清晰2、提示词技巧2:设置角色 一、什么是提示词工程 提示词工程主要是用于优化与大模型交互的提示或查询操作,其目的在于能够更加准确的获取提问者想要获取的答案,…...

RabbitMQ的事务机制
想要保证发送者一定能把消息发送给RabbitMQ,一种是通过Confirm机制,另一种就是通过事务机制。 RabbitMQ的事务机制,允许生产者将一组操作打包成一个原子事务单元,要么全部执行成功,要么全部失败。事务提供了一种确保消…...
41 物体检测和目标检测数据集【李沐动手学深度学习v2课程笔记】
目录 1. 物体检测 2. 边缘框实现 3.数据集 4. 小结 1. 物体检测 2. 边缘框实现 %matplotlib inline import torch from d2l import torch as d2ld2l.set_figsize() img d2l.plt.imread(../img/catdog.jpg) d2l.plt.imshow(img);#save def box_corner_to_center(boxes):&q…...
)
软件包管理(rpm+yum)
1.介绍软件包安装方式 rpm包安装: rpm是个软件包管理工具,通过.rpm后缀来操作 -i #安装 -q #查询 -l #列出软件包下的文件 -e #卸载 -h, #软件包安装的时候列出哈希标记 (和 -v 一起使用效果更好) -v, #提供更多的详细信息输出 rpm的痛点&#…...

网关层针对各微服务动态修改Ribbon路由策略
目录 一、介绍 二、常规的微服务设置路由算法方式 三、通过不懈努力,找到解决思路 四、验证 五、总结 一、介绍 最近,遇到这么一个需求: 1、需要在网关层(目前使用zuul)为某一个服务指定自定义算法IP Hash路由策…...
)
如何从零开始拆解uni-app开发的vue项目(二)
昨天书写了一篇如何从零开始uni-app开发的vue项目,今天准备写一篇处理界面元素动态加载的案例: 背景:有不同类别的设备,每个设备有每日检查项目、每周检查项目、每年检查项目,需要维保人员,根据不同设备和检查类别对检查项目进行处理,提交数据。 首先看一下界面: &l…...
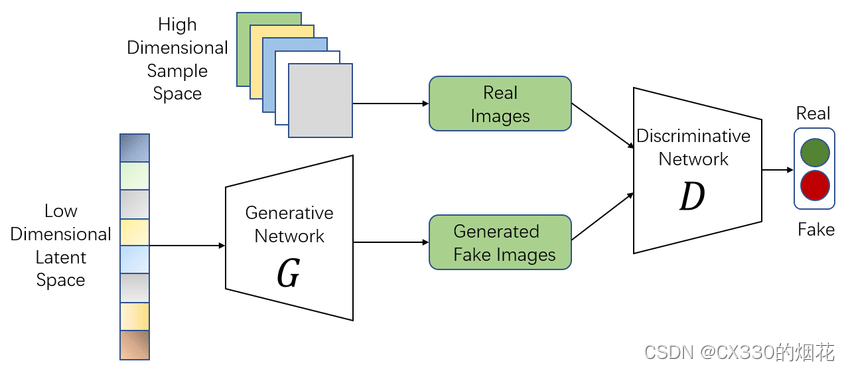
【生成对抗网络GAN】一篇文章讲透~
目录 引言 一、生成对抗网络的基本原理 1 初始化生成器和判别器 2 训练判别器 3 训练生成器 4 交替训练 5 评估和调整 二、生成对抗网络的应用领域 1 图像生成与编辑 2 语音合成与音频处理 3 文本生成与对话系统 4 数据增强与隐私保护 三、代码事例 四、生成对抗…...

【设计模式】Java 设计模式之模板命令模式(Command)
命令模式(Command)的深入分析与实战解读 一、概述 命令模式是一种将请求封装为对象从而使你可用不同的请求把客户端与接受请求的对象解耦的模式。在命令模式中,命令对象使得发送者与接收者之间解耦,发送者通过命令对象来执行请求…...

如何在Flutter中实现一键登录
获取到当前手机使用的手机卡号,直接使用这个号码进行注册、登录,这就是一键登录。 可以借助极光官方的极光认证实现 1、注册账户成为开发者 2、创建应用开通极光认证 (注意开通极光认证要通过实名审核) 3、创建应用获取appkey、 …...

Amazon SageMaker + Stable Diffusion 搭建文本生成图像模型
如果我们的计算机视觉系统要真正理解视觉世界,它们不仅必须能够识别图像,而且必须能够生成图像。文本到图像的 AI 模型仅根据简单的文字输入就可以生成图像。 近两年,以ChatGPT为代表的AIGC技术崭露头角,逐渐从学术研究的象牙塔迈…...

FPGA数字信号处理前沿
生活在这个色彩斑斓的世界里,大家的身边存在太多模拟信号比如光能、电压、电流、压力、声音、流速等。数字信号处理作为嵌入式研发的一个经久不衰热门话题,可以说大到军工武器、航空航天,小到日常仪器、工业控制,嵌入式SOC芯片数字…...

【Android】系统启动流程分析 —— init 进程启动过程
本文基于 Android 14.0.0_r2 的系统启动流程分析。 一、概述 init 进程属于一个守护进程,准确的说,它是 Linux 系统中用户控制的第一个进程,它的进程号为 1,它的生命周期贯穿整个 Linux 内核运行的始终。Android 中所有其它的进程…...

抖音视频批量下载软件可导出视频分享链接|手机网页视频提取|视频爬虫采集工具
解锁抖音视频无水印批量下载新姿势! 在快节奏的生活中,抖音作为时下最热门的短视频平台之一,吸引着广大用户的目光。而如何高效地获取喜欢的视频内容成为了许多人关注的焦点。Q:290615413现在,我们推出的抖音视频批量下载软件&…...

鸿蒙Harmony应用开发—ArkTS-@Observed装饰器和@ObjectLink装饰器:嵌套类对象属性变化
上文所述的装饰器仅能观察到第一层的变化,但是在实际应用开发中,应用会根据开发需要,封装自己的数据模型。对于多层嵌套的情况,比如二维数组,或者数组项class,或者class的属性是class,他们的第二…...
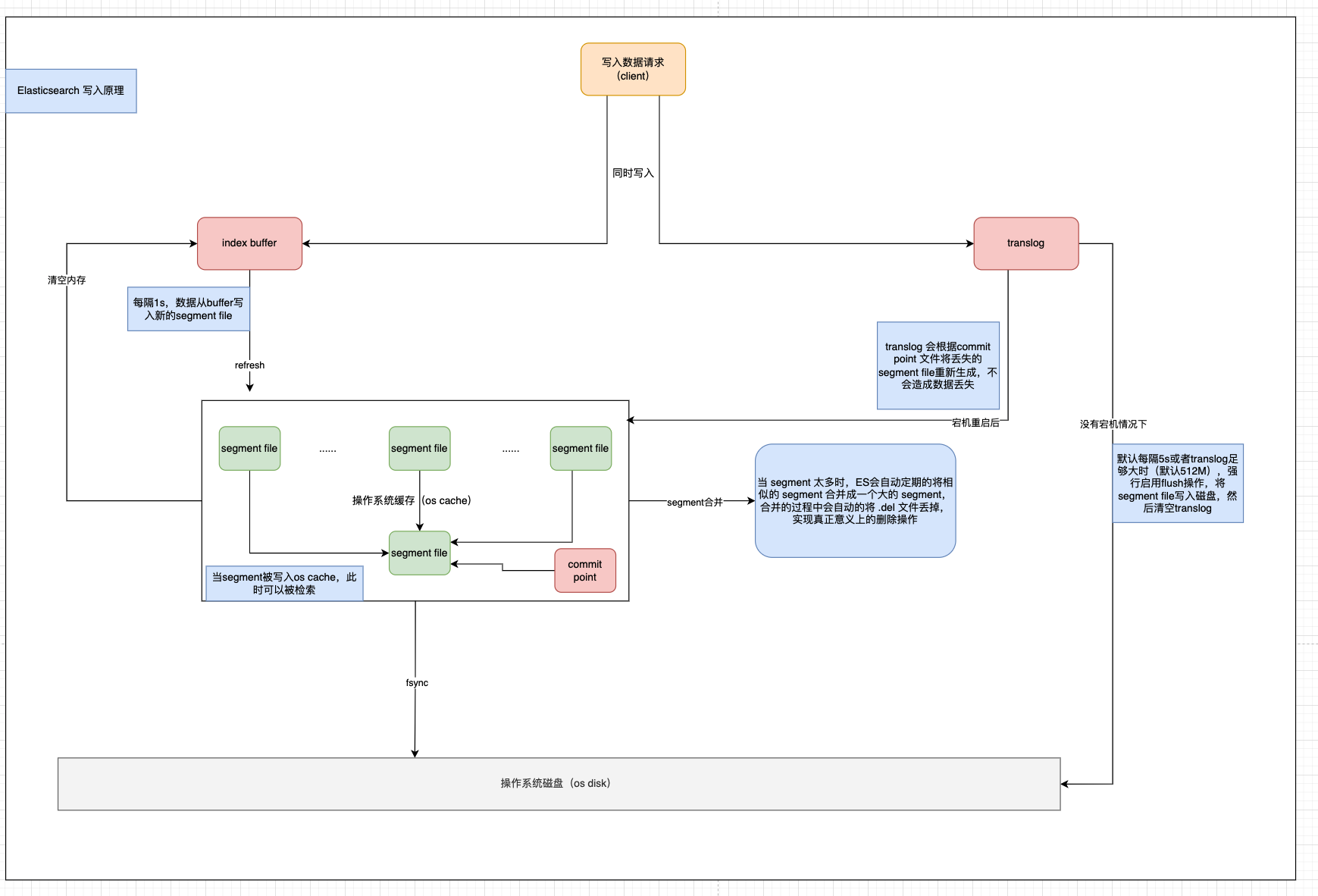
深度解析:Elasticsearch写入请求处理流程
版本 Elasticsearch 8.x 原文链接:https://mp.weixin.qq.com/s/hZ_ZOLFUoRuWyqp47hqCgQ 今天来看下 Elasticsearch 中的写入流程。 不想看过程可以直接跳转文章末尾查看总结部分。最后附上个人理解的一个图。 从我们发出写入请求,到 Elasticsearch 接收请…...
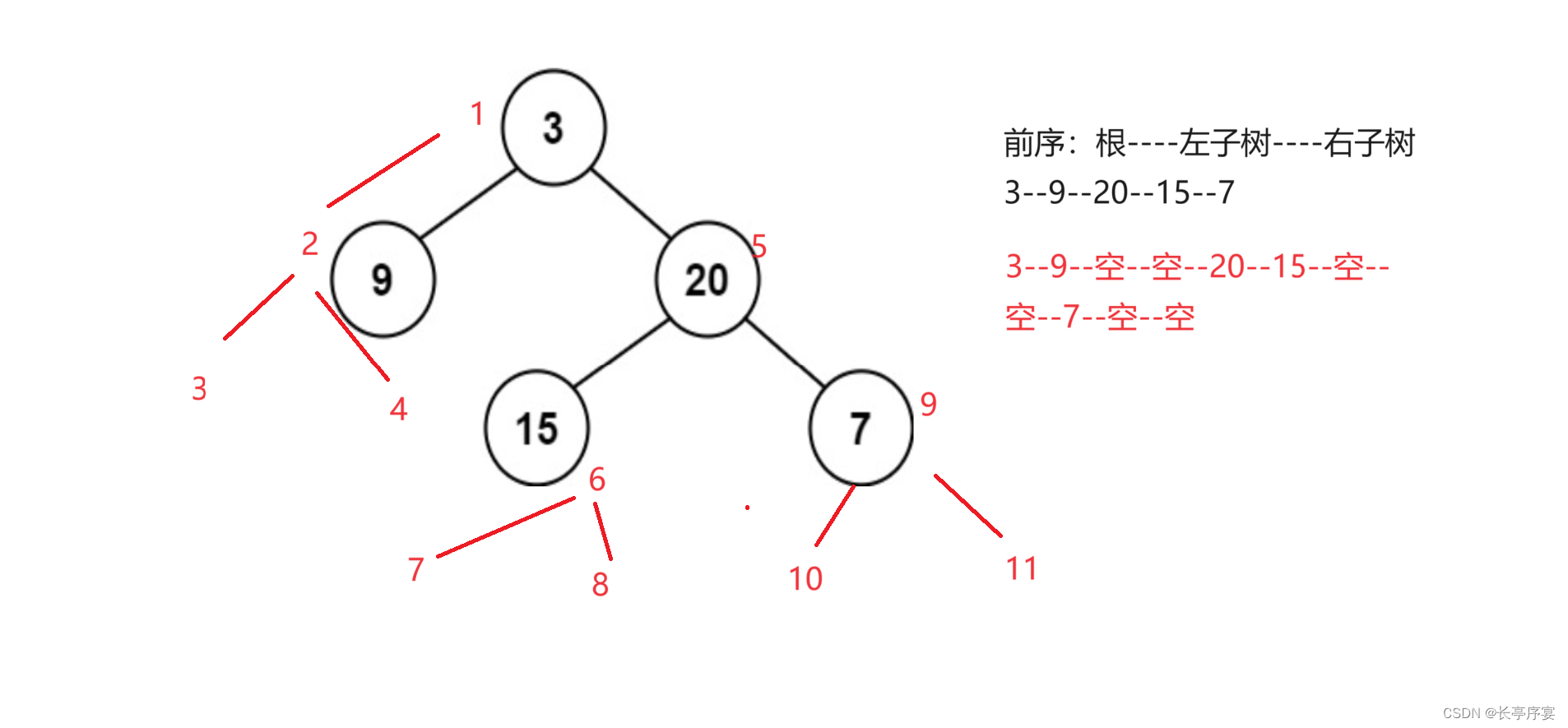
数据结构:堆和二叉树遍历
堆的特征 1.堆是一个完全二叉树 2.堆分为大堆和小堆。大堆:左右节点都小于根节点 小堆:左右节点都大于根节点 堆的应用:堆排序,topk问题 堆排序 堆排序的思路: 1.升序排序,建小堆。堆顶就是这个堆最小…...
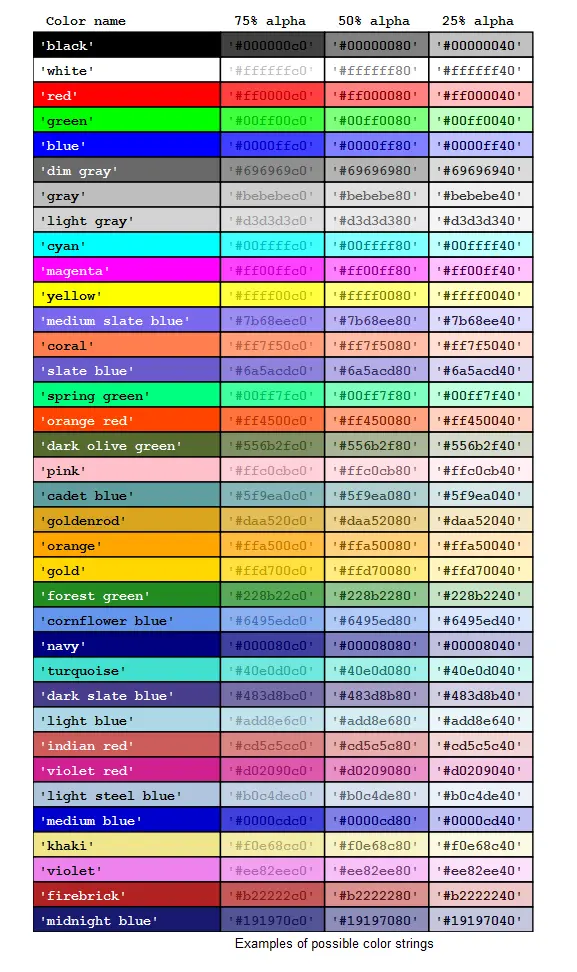
[Halcon学习笔记]在Qt上实现Halcon窗口的字体设置颜色设置等功能
1、 Halcon字体大小设置在Qt上的实现 在之前介绍过Halcon窗口显示文字字体的尺寸和样式,具体详细介绍可回看 (一)Halcon窗口界面上显示文字的字体尺寸、样式修改 当时介绍的设定方法 //Win下QString Font_win "-Arial-10-*-1-*-*-1-&q…...

ArcGis 地图文档
ArcGis官网 https://developers.arcgis.com/labs/android/create-a-starter-app/ Arcgis for android 加载谷歌、高德和天地图 https://blog.csdn.net/qq_19688207/article/details/108125778 AeroMap图层地址: API_KEY: 7e95eae2-a18d-34ce-beaa-894d6a08c5a5 街道图…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
