JavaScript高级(五)--柯西化函数
柯里化
定义
首先,我们参照维基百科给出的定义:
在计算机科学中,柯里化(英语:Currying),又译为卡瑞化或加里化,是把接受多个参数的函数变换成接受一个单一参数(最初函数的第一个参数)的函数,并且返回接受余下的参数而且返回结果的新函数的技术
例如:
简单写个sum函数:
const sum = function(a,b) {return a + b;
}// 调用
sum(1,2)
柯西化这个sum函数:
const sum = function(a) {return function(b) {return a + b;}
}
// 调用
sum(1)(2)
实现
那如果有N个参数呢,以及我要定一个函数能将所有的函数变成柯里化呢?而非仅仅是上面的sum函数
为了解决N个参数的问题,所以我们想到了递归函数。
为了解决将所有的函数变成柯里化,所以我们的入参要加上fn
function currying(fn, length) {// 第一次调用获取函数 fn 参数的长度,后续调用获取 fn 剩余参数的长度length = length || fn.length; // currying 包裹之后返回一个新函数,接收参数为 ...argsreturn function (...args) { // 新函数接收的参数长度是否大于等于 fn 剩余参数需要接收的长度return args.length >= length ? fn.apply(this, args) // 满足要求,执行 fn 函数,传入新函数的参数: currying(fn.bind(this, ...args), length - args.length) // 不满足要求,递归 currying 函数,新的 fn 为 bind 返回的新函数//(bind 绑定了 ...args 参数,未执行),新的 length 为 fn 剩余参数的长度}}const sum = function(a,b,c){return a + b + c;}const currySum = currying(sum);console.log(currySum(1,2,3));
console.log(currySum(1)(2)(3));
console.log(currySum(1,2)(3));
// 输出都是 6
快速使用
lodash中的已经带有了curry函数可以使用,使用方式如下:
const sum = function(a, b, c) {return a + b + c;
};var currySum = _.curry(abc);console.log(currySum(1,2,3));
console.log(currySum(1)(2)(3));
console.log(currySum(1,2)(3));
// 输出都是 6
柯里化的作用
提高自由度
我们可以考虑一个情况,如果对于一个函数,它有3个参数,它的作用是将3个参数相乘返回。如果我突然想乘用2个数的结果呢?是不是使用柯里化就能拿到中间的结果了。
例如bind函数:bind函数也算是提高自由度的例子
const obj = {name: "小明",
};const fn = function () {console.log(this.name);
}.bind(obj);
这里 bind 用来改变函数执行时候的上下文,但是函数本身并不执行,所以本质上是延迟计算,提高函数的自由度。
我们可以查看一下bind的简单实现,返回了函数,本身也算是一种柯里化吧。
// 简化实现,完整版实现中的第 2 步
Function.prototype.bind = function (context) {var self = this;// 第 1 个参数是指定的 this,截取保存第 1 个之后的参数// arr.slice(begin); 即 [begin, end]var args = Array.prototype.slice.call(arguments, 1); return function () {// 此时的 arguments 是指 bind 返回的函数调用时接收的参数// 即 return function 的参数,和上面那个不同// 类数组转成数组var bindArgs = Array.prototype.slice.call(arguments);// 执行函数return self.apply( context, args.concat(bindArgs) );}
}
相关文章:
--柯西化函数)
JavaScript高级(五)--柯西化函数
柯里化 定义 首先,我们参照维基百科给出的定义: 在计算机科学中,柯里化(英语:Currying),又译为卡瑞化或加里化,是把接受多个参数的函数变换成接受一个单一参数(最初函数…...

带3090显卡的Linux服务器上部署SDWebui
背景 一直在研究文生图,之前一直是用原始模型和diffuser跑SD模型,近来看到不少比较博主在用 SDWebui,于是想着在Linux服务器上部署体验一下,谁知道并没有想象的那么顺利,还是踩了不少坑。记录一下过程,也许…...
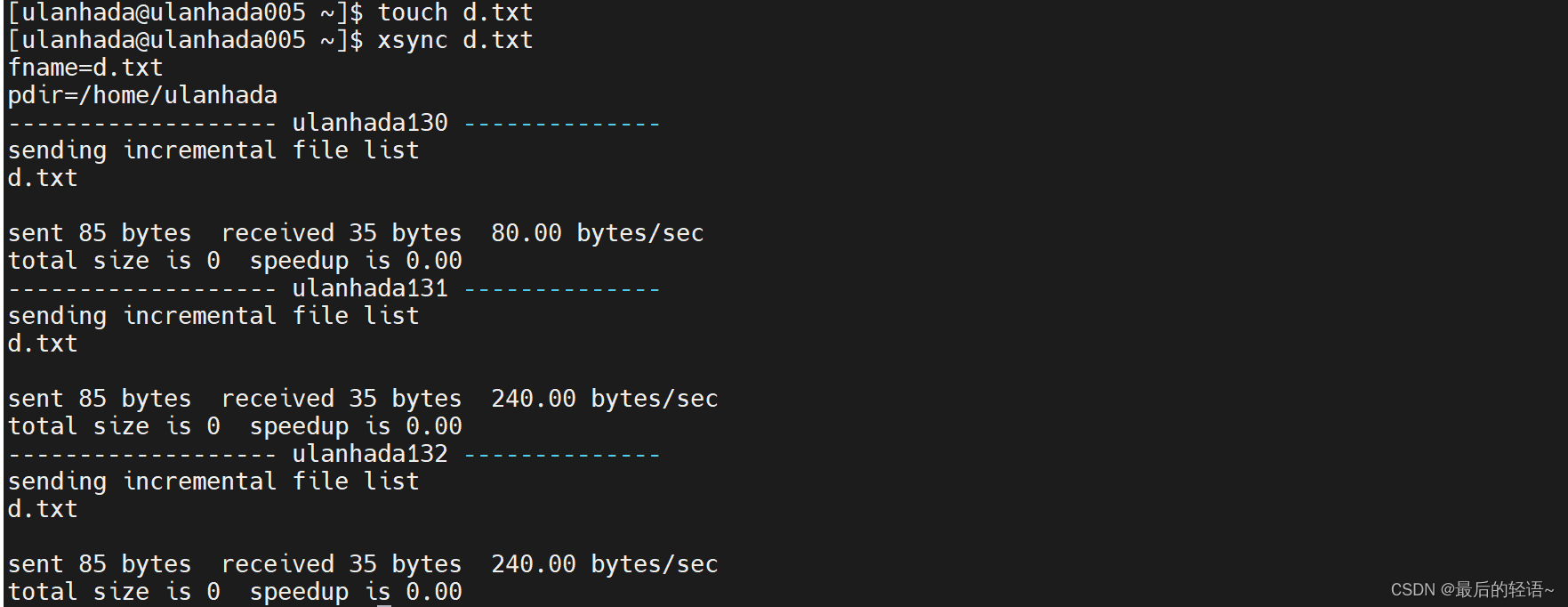
37、Linux中Xsync数据同步备份工具
37、Linux中Xsync数据同步备份工具 一、介绍二、配置集群hostname三、修改xsync文件四、赋权五、安装Rsync六、验证一七、配置免密登录1、生成rsa密钥2、copy机器自身公钥到目标机器3、.ssh/文件目录赋权 八、验证二 ⚠️ 注:本文全程在普通用户下操作,…...

网络基础:构建你的数字世界之桥
I. 引言 A. 什么是网络? 网络是由各种电子设备通过通信线路或无线电波连接起来,以便彼此之间进行数据交换和资源共享的系统。在当今数字化时代,网络已经成为我们生活和工作中不可或缺的一部分,无论是互联网、局域网还是无线通信…...
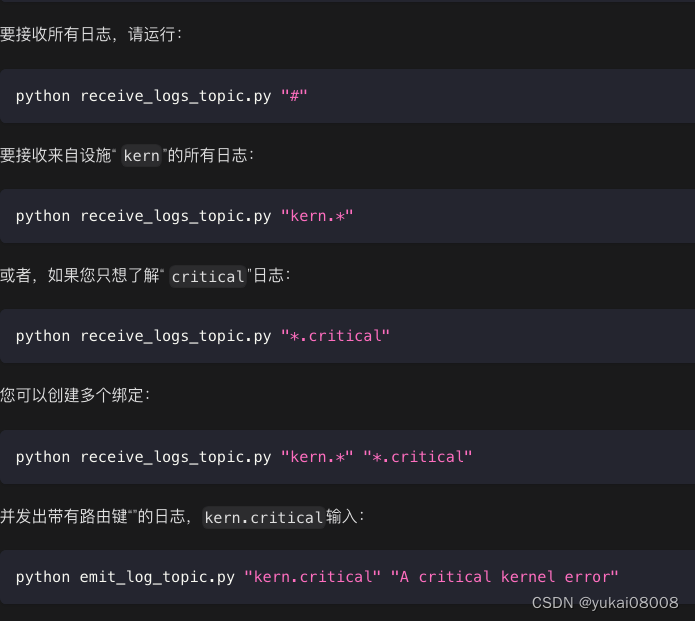
Python 全栈系列236 rabbit_agent搭建
说明 通过rabbit_agent, 以接口方式实现对队列的标准操作,将pika包在微服务内,而不必在太多地方重复的去写。至少在服务端发布消息时,不必再去考虑这些问题。 在分布式任务的情况下,客户端本身会启动一个持续监听队列的客户端服…...

管理自由,体验简单,使用安全 | 详解威联通全套多用户多权限管理方案【附TS-466C产品介绍】
管理自由,体验简单,使用安全 | 详解威联通全套多用户多权限管理方案【附TS-466C产品介绍】 哈喽小伙伴们好,我是Stark-C~。今天我们来解决一个之前评论区多次被提及的问题--多用户权限管理。 对于我们NAS用户来说,基本都会面临这…...
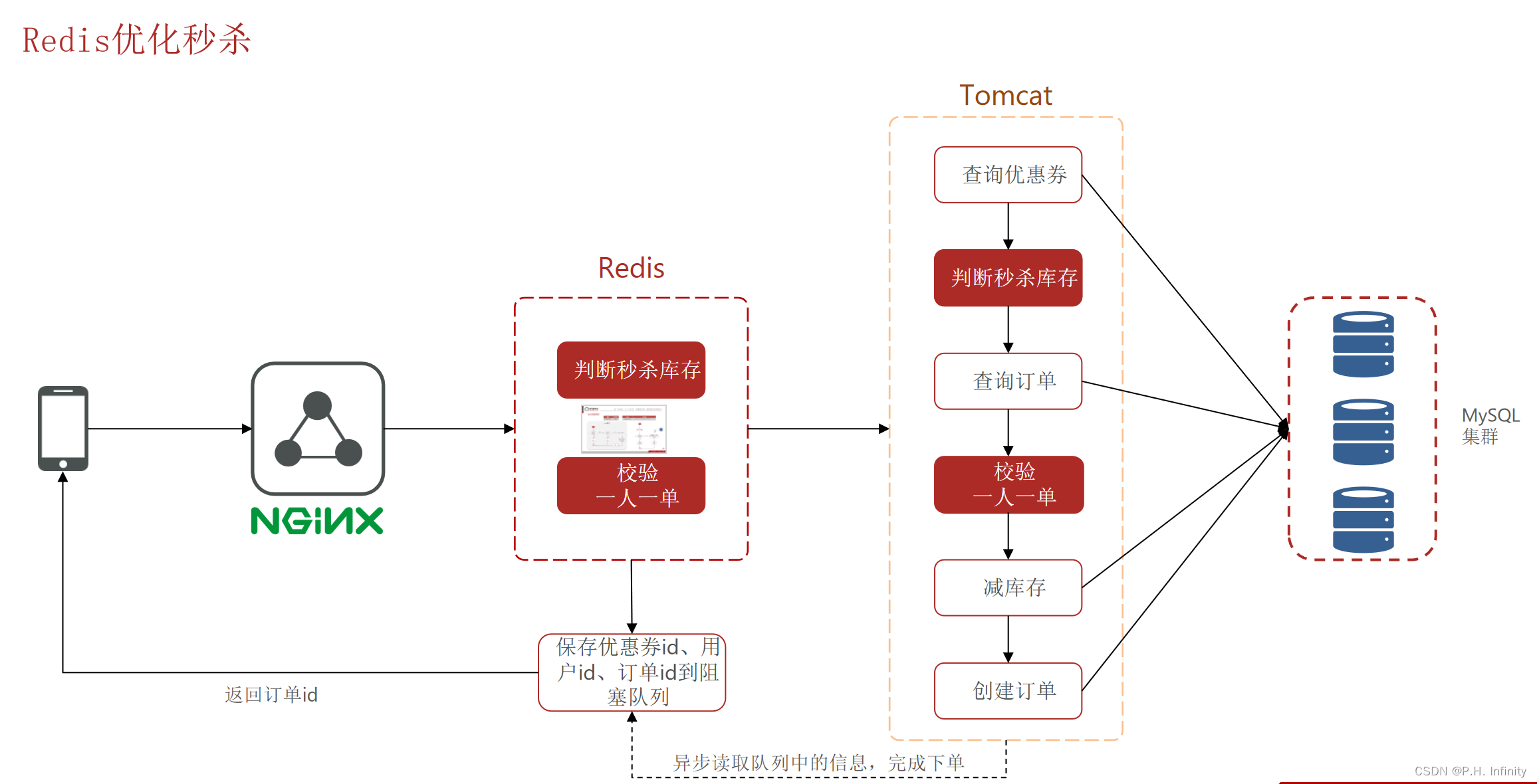
【Redis】优惠券秒杀
全局唯一ID 全局唯一ID生成策略: UUIDRedis自增snowflake算法数据库自增 Redis自增ID策略:每天一个key,方便统计订单量ID构造是 时间戳 计数器 Component public class RedisIdWorker {// 2024的第一时刻private static final long BEGIN…...

【几何】平面方程
文章目录 平面方程一般式截距式点法式法线式 平面方程 平面方程是用一个方程来表示平面,平面上的所有点代入方程,方程都成立。因为用法的不同,平面方程一般有四种表现形式。 一般式 设 n ⃗ ( A , B , C ) \vec n(A,B,C) n (A,B,C) 为平…...

macOS访问samba文件夹的正确姿势,在哪里更改“macOS的连接身份“?还真不好找!
环境:路由器上需要身份认证的Mini NAS macOS Sonoma 14 这是一个非常简单的问题,但解决方法却藏得比较深,不够直观,GPT也没有给出明确的解决提示,特意记录一下。 macOS很多地方都很自动,有时候让人找不到设…...

linux进程切换
内核堆栈:每个进程在内核模式下运行时都有自己的内核堆栈。这个堆栈保存了进程在内核模式下的运行状态,包括函数调用时传递的参数、局部变量和返回地址等。 用户态与内核态:进程通常在用户态下运行,当执行系统调用或响应中断时进…...

spring boot 如何升级 Tomcat 版本
在Spring Boot应用程序中升级内嵌的Tomcat版本通常涉及以下几个步骤: 1. 确定当前使用的Tomcat版本 首先,你需要确定你的Spring Boot应用程序当前使用的Tomcat版本。这可以通过查看项目的pom.xml或build.gradle文件来完成,其中会列出所有的…...
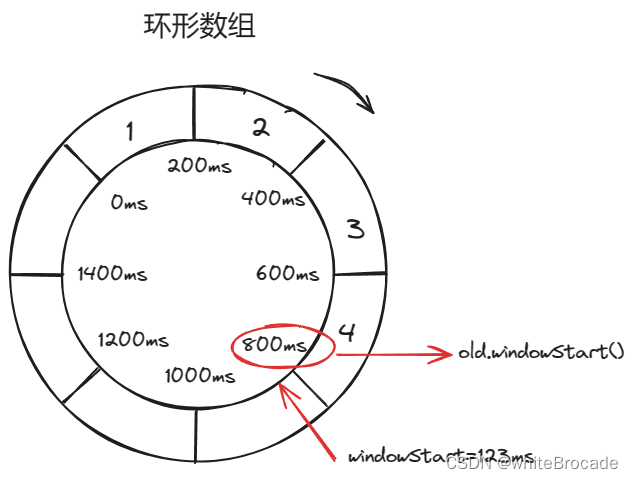
sentinel中StatisticSlot数据采集的原理
StatisticSlot数据采集的原理 时间窗口 固定窗口 在固定的时间窗口内,可以允许固定数量的请求进入;超过数量就拒绝或者排队,等下一个时间段进入, 如下图 时间窗长度划分为1秒 单个时间窗的请求阈值为3 上述存在一个问题, 假如9:18:04:…...

图像去噪与增强技术
图像去噪与增强技术是数字图像处理领域中的两个重要方面,它们分别关注消除图像中的噪声和改善图像的质量。 图像去噪技术的主要目的是从受噪声干扰的图像中去除不必要的随机信号,以恢复图像的真实内容。这对于图像的进一步分析和理解至关重要。去噪技术包…...

SpringJPA 做分页条件查询
前言: 相信小伙伴们的项目很多都用到SpringJPA框架的吧,对于单表的增删改查利用jpa是很方便的,但是对于条件查询并且分页 是不是很多小伙伴不经常写到. 今天我整理了一下在这里分享一下. 话不多说直接上代码: Controller: RestController public class ProductInstanceContr…...
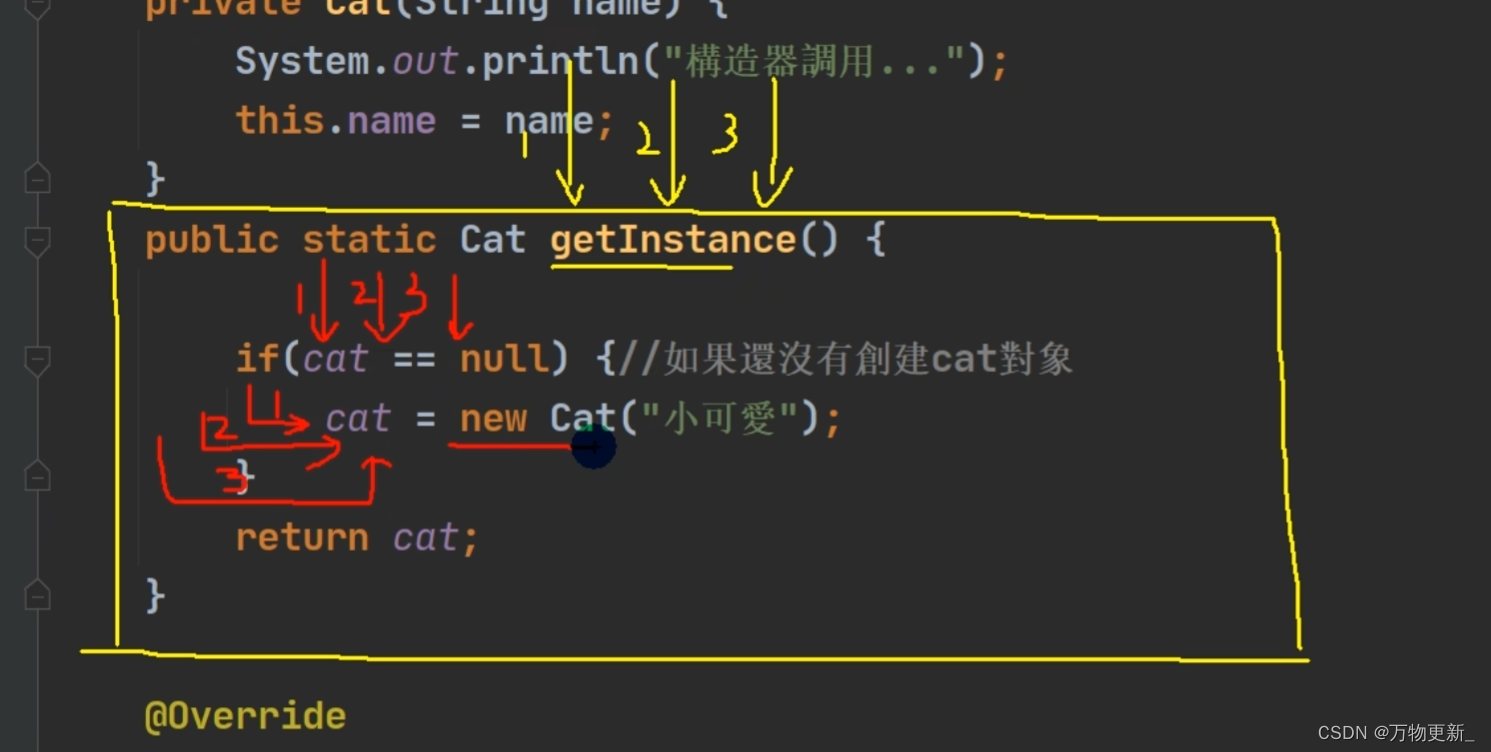
[Java基础揉碎]单例模式
目录 什么是设计模式 什么是单例模式 饿汉式与懒汉式 饿汉式vs懒汉式 懒汉式存在线程安全问题 什么是设计模式 1.静态方法和属性的经典使用 2.设计模式是在大量的实践中总结和理论化之后优选的代码结构、编程风格、 以及解决问题的思考方式。设计模式就像是经典的棋谱&am…...
unity无法使用道路生成插件Road Architect(ctrl和shift无法标点)
切换一下布局就行了。 附:Road Architect教学地址...
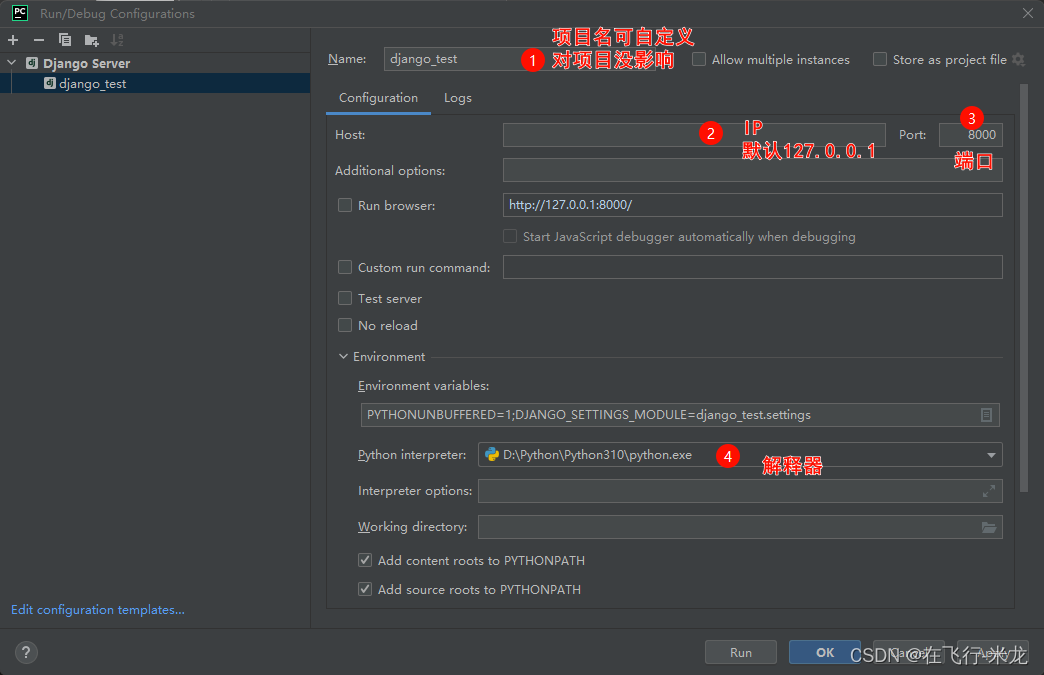
Django下载使用、文件介绍
【一】下载并使用 【1】下载框架 (1)注意事项 计算机名称不要出现中文python解释器版本不同可能会出现启动报错项目中所有的文件名称不要出现中文多个项目文件尽量不要嵌套,做到一项一夹 (2)下载 Django属于第三方模块&#…...

Docker进阶:Docker-cpmpose 实现服务弹性伸缩
Docker进阶:Docker-cpmpose 实现服务弹性伸缩 一、Docker Compose基础概念1.1 Docker Compose简介1.2 Docker Compose文件结构 二、弹性伸缩的原理和实现步骤2.1 弹性伸缩原理2.2 实现步骤 三、技术实践案例3.1 场景描述3.2 配置Docker Compose文件3.3 使用 docker-…...

opencv各个模块介绍(2)
Features2D 模块:特征检测和描述子计算模块,包括SIFT、SURF等算法。 Features2D 模块提供了许多用于特征检测和描述子匹配的函数和类,这些函数和类可用于图像特征的提取、匹配和跟踪。 FeatureDetector:特征检测器的基类…...
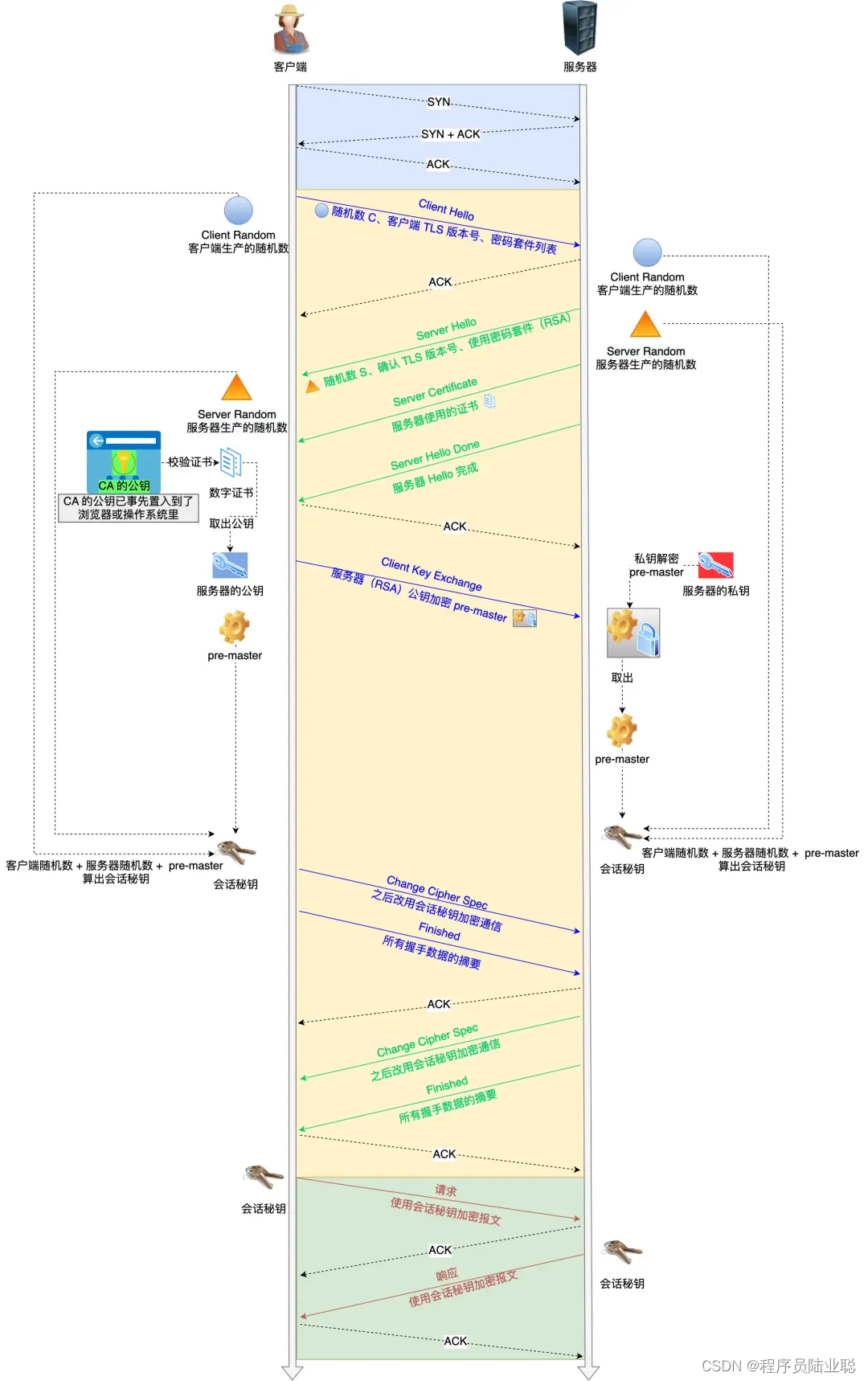
HTTPS:原理、使用方法及安全威胁
文章目录 一、HTTPS技术原理1.1 主要技术原理1.2 HTTPS的工作过程1.2.1 握手阶段1.2.2 数据传输阶段 1.3 HTTPS的安全性 二、HTTPS使用方法三、HTTPS安全威胁四、总结 HTTPS(全称:Hyper Text Transfer Protocol over Secure Socket Layer)&am…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
