【几何】平面方程
文章目录
- 平面方程
- 一般式
- 截距式
- 点法式
- 法线式
平面方程
平面方程是用一个方程来表示平面,平面上的所有点代入方程,方程都成立。因为用法的不同,平面方程一般有四种表现形式。
一般式
设 n ⃗ = ( A , B , C ) \vec n=(A,B,C) n=(A,B,C) 为平面的法线, p 0 ( x 0 , y 0 , z 0 ) p_0(x_0, y_0, z_0) p0(x0,y0,z0) 、 p ( x , y , z ) p(x, y, z) p(x,y,z) 为平面上两点。我们知道两个垂直向量的点乘为0,则平面的法线和平面上两点组成向量的点乘也为0,则 n ⃗ ∗ p 0 p → = 0 \vec n * \overrightarrow {p_0p} = 0 n∗p0p=0 , 可以得出
n ⃗ ∗ ( p − p 0 ) = 0 n ⃗ ∗ p − n ⃗ ∗ p 0 = 0 由于 n ⃗ 和 p 0 已知,设常数 D = − n ⃗ ∗ p 0 , 则 n ⃗ ∗ p + D = 0 A ∗ x + B ∗ y + C ∗ z + D = 0 \vec n * (p - p_0) = 0 \\ \vec n * p - \vec n * p_0 = 0 \\ 由于\vec n和p_0已知,设常数D = -\vec n * p_0,则 \\ \vec n * p + D = 0 \\ A*x+B*y+C*z+D=0 n∗(p−p0)=0n∗p−n∗p0=0由于n和p0已知,设常数D=−n∗p0,则n∗p+D=0A∗x+B∗y+C∗z+D=0
平面的一般式为 A ∗ x + B ∗ y + C ∗ z + D = 0 A*x+B*y+C*z+D=0 A∗x+B∗y+C∗z+D=0,其中 ( A , B , C ) (A, B, C) (A,B,C)为平面的法线, − D -D −D为原点 o ( 0 , 0 , 0 ) o(0,0,0) o(0,0,0)到平面的垂直距离, n ⃗ ∗ p 0 = n ⃗ ∗ o p 0 → \vec n * p_0 = \vec n * \overrightarrow {op_0} n∗p0=n∗op0,为 o p 0 → \overrightarrow {op_0} op0在 n ⃗ \vec n n方向上的投影距离。
截距式
现在已知平面的一般式为 A ∗ x + B ∗ y + C ∗ z + D = 0 A*x+B*y+C*z+D=0 A∗x+B∗y+C∗z+D=0,
设 a = − D / A , b = − D / B , c = − D / C a=-D/A,b=-D/B,c=-D/C a=−D/A,b=−D/B,c=−D/C, 则 A = − D / a , B = − D / b , c = − D / C A=-D/a,B=-D/b,c=-D/C A=−D/a,B=−D/b,c=−D/C, 原式可改为
− D a ∗ x − D b ∗ y − D c ∗ z + D = 0 − D ∗ ( 1 a ∗ x + 1 b ∗ y + 1 c ∗ z ) + D = 0 1 a ∗ x + 1 b ∗ y + 1 c ∗ z = 1 -\frac{D}{a}*x-\frac{D}{b}*y-\frac{D}{c}*z+D=0 \\ -D*(\frac{1}{a}*x+\frac{1}{b}*y+\frac{1}{c}*z)+D=0 \\ \frac{1}{a}*x+\frac{1}{b}*y+\frac{1}{c}*z=1 \\ −aD∗x−bD∗y−cD∗z+D=0−D∗(a1∗x+b1∗y+c1∗z)+D=0a1∗x+b1∗y+c1∗z=1
平面的截距式为 1 a ∗ x + 1 b ∗ y + 1 c ∗ z = 1 \frac{1}{a}*x+\frac{1}{b}*y+\frac{1}{c}*z=1 a1∗x+b1∗y+c1∗z=1,其中 a , b , c a,b,c a,b,c分别为平面与xyz轴的交点。
点法式
已知平面的法线 n ⃗ \vec n n 和平面上的两点 p 、 p 0 p、p_0 p、p0 ,求平面的方程。和上面一般式的求取过程是一样的,只不过得到的最后的表达方式不同。
n ⃗ ∗ ( p − p 0 ) = 0 A ∗ ( x − x 0 ) + B ∗ ( y − y 0 ) + C ∗ ( c − c 0 ) = 0 \vec n * (p - p_0) = 0 \\ A*(x-x_0)+B*(y-y_0)+C*(c-c_0)=0 n∗(p−p0)=0A∗(x−x0)+B∗(y−y0)+C∗(c−c0)=0
平面的点法式为 A ∗ ( x − x 0 ) + B ∗ ( y − y 0 ) + C ∗ ( c − c 0 ) = 0 A*(x-x_0)+B*(y-y_0)+C*(c-c_0)=0 A∗(x−x0)+B∗(y−y0)+C∗(c−c0)=0,其中 ( A , B , C ) (A, B, C) (A,B,C)为平面的法线, ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0) 为平面上的一点。
法线式
已知平面的法线和原点到平面的距离,求平面的方程。法线式和一般式几乎是一样的。
n ⃗ = ( A , B , C ) \vec n=(A,B,C) n=(A,B,C) ,那么 n ⃗ \vec n n 与xyz三个坐标轴的余弦值是多少呢?
设 n ⃗ \vec n n 与xyz的夹角分别为 α , β , γ \alpha,\beta,\gamma α,β,γ ,则
cos α = ( A , B , C ) ∗ ( 1 , 0 , 0 ) = A cos β = ( A , B , C ) ∗ ( 0 , 1 , 0 ) = B cos γ = ( A , B , C ) ∗ ( 0 , 0 , 1 ) = C 则 cos α ∗ x + cos β ∗ y + cos γ ∗ z + D = 0 设 p = − D , 得 cos α ∗ x + cos β ∗ y + cos γ ∗ z = p \cos \alpha=(A,B,C)*(1,0,0)=A \\ \cos \beta=(A,B,C)*(0,1,0)=B \\ \cos \gamma=(A,B,C)*(0,0,1)=C \\ 则\cos \alpha*x+\cos \beta*y+\cos \gamma*z+D=0 \\ 设p=-D,得 \cos \alpha*x+\cos \beta*y+\cos \gamma*z=p cosα=(A,B,C)∗(1,0,0)=Acosβ=(A,B,C)∗(0,1,0)=Bcosγ=(A,B,C)∗(0,0,1)=C则cosα∗x+cosβ∗y+cosγ∗z+D=0设p=−D,得cosα∗x+cosβ∗y+cosγ∗z=p
平面的法线式为 cos α ∗ x + cos β ∗ y + cos γ ∗ z = p \cos \alpha*x+\cos \beta*y+\cos \gamma*z=p cosα∗x+cosβ∗y+cosγ∗z=p ,其中 ( cos α , cos β , cos γ ) (\cos \alpha,\cos \beta,\cos \gamma) (cosα,cosβ,cosγ) 为平面的法线, p p p 为原点离平面的垂直距离。
相关文章:

【几何】平面方程
文章目录 平面方程一般式截距式点法式法线式 平面方程 平面方程是用一个方程来表示平面,平面上的所有点代入方程,方程都成立。因为用法的不同,平面方程一般有四种表现形式。 一般式 设 n ⃗ ( A , B , C ) \vec n(A,B,C) n (A,B,C) 为平…...

macOS访问samba文件夹的正确姿势,在哪里更改“macOS的连接身份“?还真不好找!
环境:路由器上需要身份认证的Mini NAS macOS Sonoma 14 这是一个非常简单的问题,但解决方法却藏得比较深,不够直观,GPT也没有给出明确的解决提示,特意记录一下。 macOS很多地方都很自动,有时候让人找不到设…...

linux进程切换
内核堆栈:每个进程在内核模式下运行时都有自己的内核堆栈。这个堆栈保存了进程在内核模式下的运行状态,包括函数调用时传递的参数、局部变量和返回地址等。 用户态与内核态:进程通常在用户态下运行,当执行系统调用或响应中断时进…...

spring boot 如何升级 Tomcat 版本
在Spring Boot应用程序中升级内嵌的Tomcat版本通常涉及以下几个步骤: 1. 确定当前使用的Tomcat版本 首先,你需要确定你的Spring Boot应用程序当前使用的Tomcat版本。这可以通过查看项目的pom.xml或build.gradle文件来完成,其中会列出所有的…...
sentinel中StatisticSlot数据采集的原理
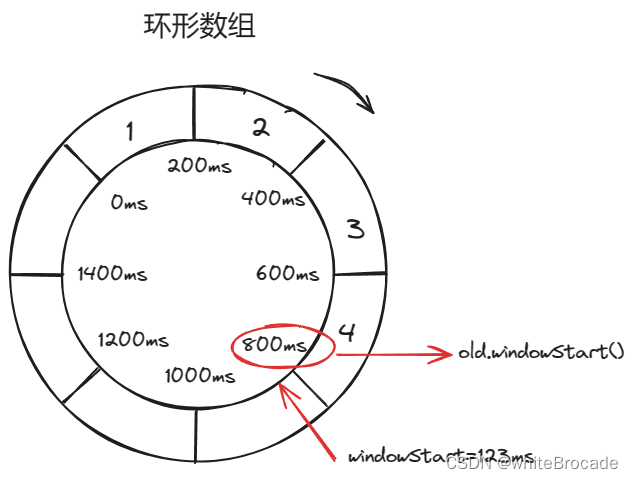
StatisticSlot数据采集的原理 时间窗口 固定窗口 在固定的时间窗口内,可以允许固定数量的请求进入;超过数量就拒绝或者排队,等下一个时间段进入, 如下图 时间窗长度划分为1秒 单个时间窗的请求阈值为3 上述存在一个问题, 假如9:18:04:…...

图像去噪与增强技术
图像去噪与增强技术是数字图像处理领域中的两个重要方面,它们分别关注消除图像中的噪声和改善图像的质量。 图像去噪技术的主要目的是从受噪声干扰的图像中去除不必要的随机信号,以恢复图像的真实内容。这对于图像的进一步分析和理解至关重要。去噪技术包…...

SpringJPA 做分页条件查询
前言: 相信小伙伴们的项目很多都用到SpringJPA框架的吧,对于单表的增删改查利用jpa是很方便的,但是对于条件查询并且分页 是不是很多小伙伴不经常写到. 今天我整理了一下在这里分享一下. 话不多说直接上代码: Controller: RestController public class ProductInstanceContr…...
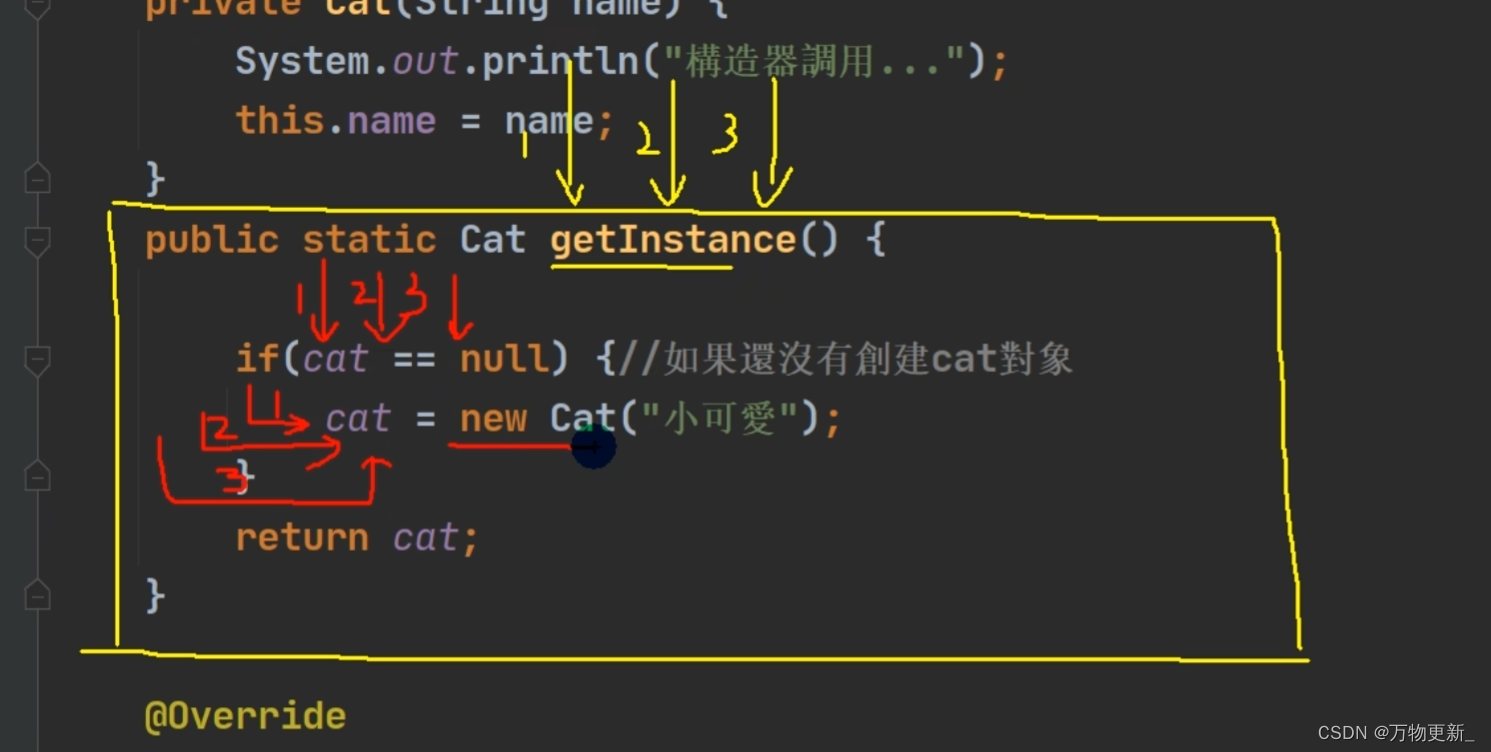
[Java基础揉碎]单例模式
目录 什么是设计模式 什么是单例模式 饿汉式与懒汉式 饿汉式vs懒汉式 懒汉式存在线程安全问题 什么是设计模式 1.静态方法和属性的经典使用 2.设计模式是在大量的实践中总结和理论化之后优选的代码结构、编程风格、 以及解决问题的思考方式。设计模式就像是经典的棋谱&am…...
unity无法使用道路生成插件Road Architect(ctrl和shift无法标点)
切换一下布局就行了。 附:Road Architect教学地址...
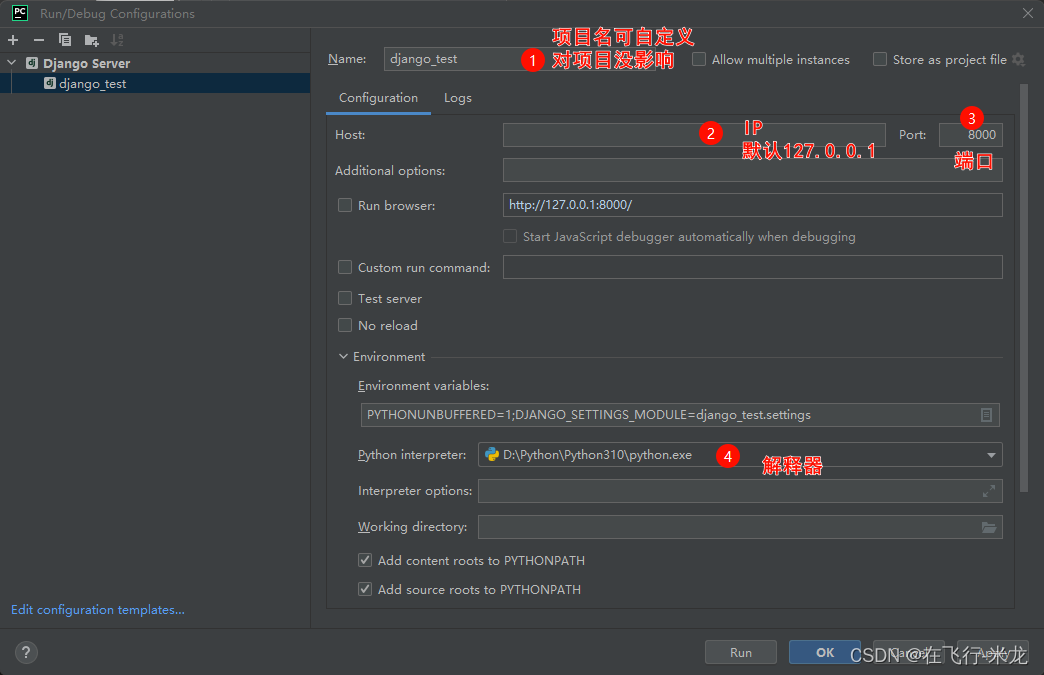
Django下载使用、文件介绍
【一】下载并使用 【1】下载框架 (1)注意事项 计算机名称不要出现中文python解释器版本不同可能会出现启动报错项目中所有的文件名称不要出现中文多个项目文件尽量不要嵌套,做到一项一夹 (2)下载 Django属于第三方模块&#…...

Docker进阶:Docker-cpmpose 实现服务弹性伸缩
Docker进阶:Docker-cpmpose 实现服务弹性伸缩 一、Docker Compose基础概念1.1 Docker Compose简介1.2 Docker Compose文件结构 二、弹性伸缩的原理和实现步骤2.1 弹性伸缩原理2.2 实现步骤 三、技术实践案例3.1 场景描述3.2 配置Docker Compose文件3.3 使用 docker-…...

opencv各个模块介绍(2)
Features2D 模块:特征检测和描述子计算模块,包括SIFT、SURF等算法。 Features2D 模块提供了许多用于特征检测和描述子匹配的函数和类,这些函数和类可用于图像特征的提取、匹配和跟踪。 FeatureDetector:特征检测器的基类…...
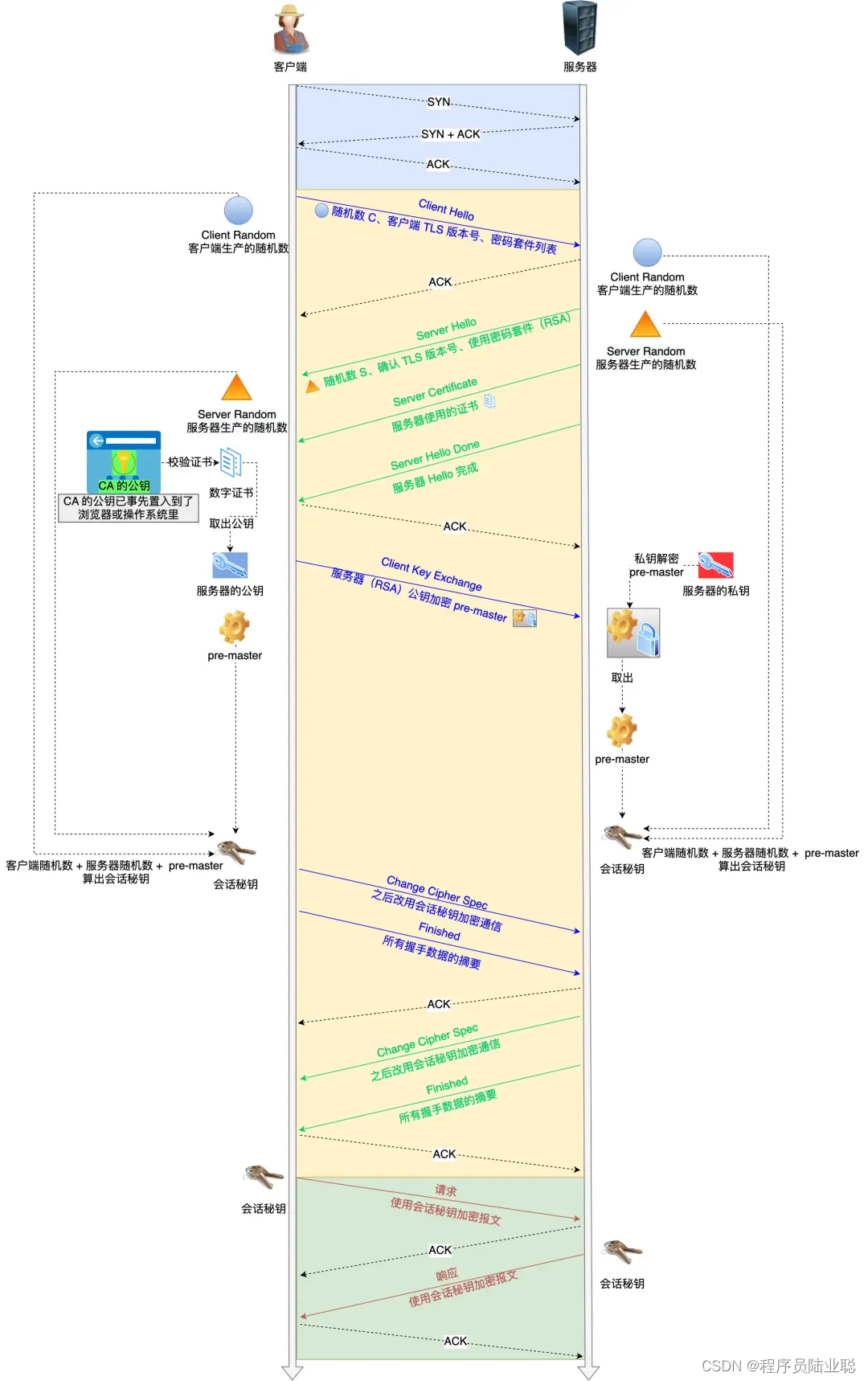
HTTPS:原理、使用方法及安全威胁
文章目录 一、HTTPS技术原理1.1 主要技术原理1.2 HTTPS的工作过程1.2.1 握手阶段1.2.2 数据传输阶段 1.3 HTTPS的安全性 二、HTTPS使用方法三、HTTPS安全威胁四、总结 HTTPS(全称:Hyper Text Transfer Protocol over Secure Socket Layer)&am…...

【云开发笔记No.6】腾讯CODING平台
腾讯云很酷的一个应用,现在对于研发一体化,全流程管理,各种工具层出不穷。 云时代用云原生,再加上AI,编码方式真是发生了质的变化。 从前,一个人可以写一个很酷的软件,后来,这变得…...

20.Ubuntu下安装GCC
文章目录 Ubuntu下安装GCC查看官方安装指导错误缺少gmp库缺少32位开发库libcg: error: gengtype-lex.c: No such file or directoryreference 欢迎访问个人网络日志🌹🌹知行空间🌹🌹 Ubuntu下安装GCC 为了支持新的c标准ÿ…...

2.windows ubuntu子系统配置
打开UBuntu后, > wget https://mirrors.tuna.tsinghua.edu.cn/anaconda/miniconda/Miniconda3-latest-Linux-x86_64.sh #下载conda软件。 > bash Miniconda3-latest-Linux-x86_64.sh #下载完conda后执行这步 > source ~/.bashrc > conda-h #出现一下…...
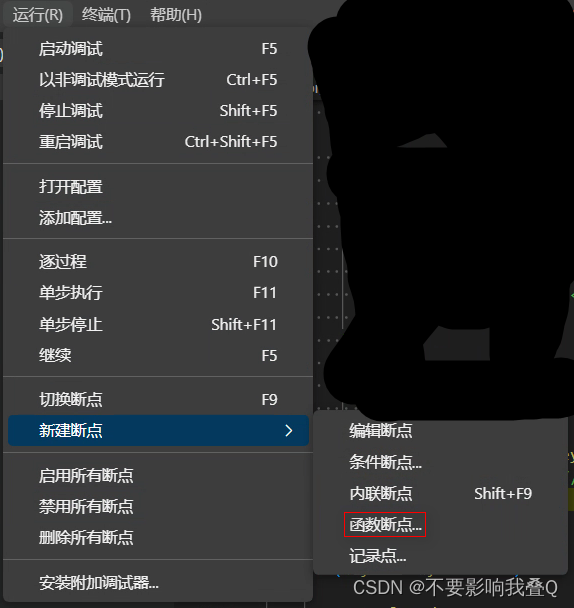
vscode的一些技巧
技巧1:调试时传参数 在launch.json的configuration中"pwd"或者"program"选项之后添加如下选项: “--args”:["参数1", "参数2", ..., "参数3] 参数之间使用逗号隔开 技巧2:断点 普通断点使…...

JavaEE企业级分布式高级架构师课程
教程介绍 本课程主要面向1-5年及以上工作经验的Java工程师,大纲由IT界知名大牛 — 廖雪峰老师亲自打造,由来自一线大型互联网公司架构师、技术总监授课,内容涵盖深入spring5设计模式/高级web MVC开发/高级数据库设计与开发/高级响应式web开发…...
)
c语言函数大全(K开头)
c语言函数大全(K开头) There is no nutrition in the blog content. After reading it, you will not only suffer from malnutrition, but also impotence. The blog content is all parallel goods. Those who are worried about being cheated should leave quickly. 函数名…...

高效备考2025年AMC8竞赛:吃透2000-2024年600道真题(免费送题)
我们继续来随机看五道AMC8的真题和解析,根据实践经验,对于想了解或者加AMC8美国数学竞赛的考生来说,吃透AMC8历年真题是备考更加科学、有效的方法之一。 最近有家长朋友问我,现在有哪些类似于奥数的比赛可以参加?我的…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...
