高效备考2025年AMC8竞赛:吃透2000-2024年600道真题(免费送题)
我们继续来随机看五道AMC8的真题和解析,根据实践经验,对于想了解或者加AMC8美国数学竞赛的考生来说,吃透AMC8历年真题是备考更加科学、有效的方法之一。
最近有家长朋友问我,现在有哪些类似于奥数的比赛可以参加?我的建议可以关注下AMC8的竞赛,类似于国内的奥数,但是其难度要比国内的奥数低一些,而且比赛门槛更低,考试也更方便。比赛的题目尤其是应用题比较有趣,题目是中英文对照的,不用担心孩子英语的问题。
另一个方面,即使不参加AMC8竞赛,吃透了历年真题600道和背后的知识体系,那么小学和初中数学一定会学得非常轻松、游刃有余。(我个人建议孩子有余力的情况下还是参加,以赛促学是一种很不错的做法,能够激发孩子的好胜心和学习热情,也是孩子宝贵的经历、体验。)

为帮助孩子们更高效地备考,我整理了2000-2004年的全部AMC8真题(完整版共600道,且修正了原试卷中的少量bug),并且独家制作了多种在线练习,利用碎片化时间,一年足以通过自学在2025年AMC8竞赛中取得好成绩。详情见文末。
好消息,2000-2024年官方发布的高清版AMC8的真题和答案免费赠送,在线练习集免费体验,如有需要的朋友们欢迎联系。
2000-2024年AMC8真题和解析:2019年第7题

这道题的考点是算术、代数,列一元一次方程解应用题。
我们假设Shauna最后2场考试的分数分别为x和y,那么可以得到方程:(76+94+87+x+y)/5=81,即(257+x+y)/5=81,即257+x+y=405,x+y=148。即Shauna最后2场考试的总分为148分不变,要使得其中一场考试分数最低,则需要令另外一场考试的分数最高,最高是100 分,那么这场考试最低是48。答案选A。
2000-2024年AMC8真题和解析:2019年第8题

这道题的考点是百分数。
我们假设Gilda原来有100个玻璃球,那么第一次给出20%后,还剩100*(1-20%)=80个。第二次给出剩下的10%后,还剩:80*(1-10%)=72个。第3次给出剩下的25%后,还剩下:72*(1-25%)=54个,这占原来总数100个的54%,所以答案选E。
提醒:在比赛时,有的考生假设Gilda原来有玻璃球x个,然后把x代入计算,也能得出正确答案。不过这里直接假设100个是最快速的。要学会用这种假设、代数法。
2000-2024年AMC8真题和解析:2014年第11题

这道题考点是排列组合,我们先根据题意画出如下示意图。
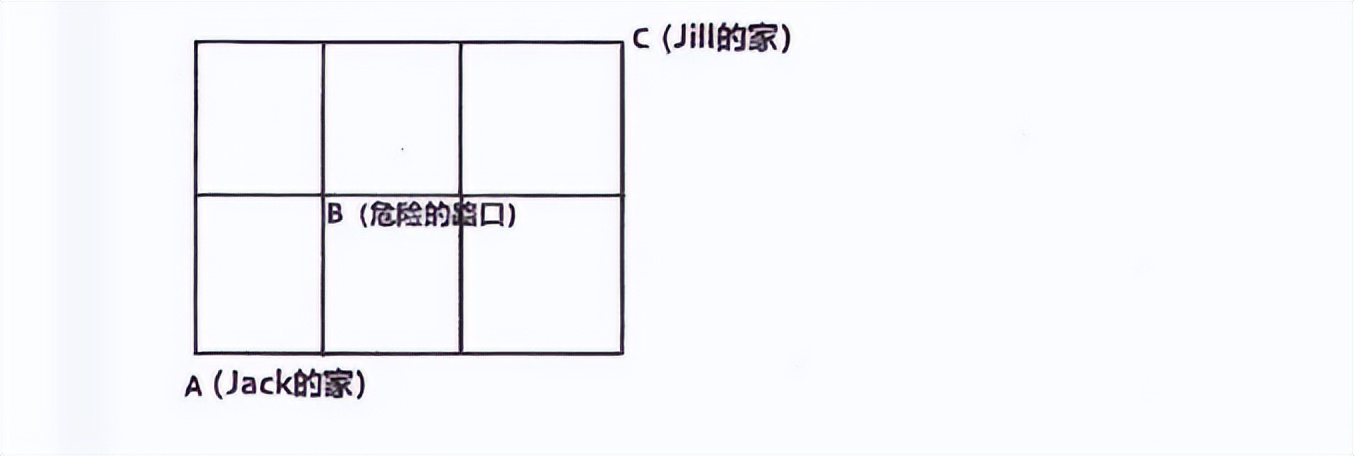
我们可以先算出经过这个危险的十字路口的方法数,然后将总方法数减去这个方法数,所得的差即为符合题意的方法数。
如上图所示,假设左下角A为Jack的家,右上角C点为Jill的家,B点为危险的十字路口。从A到B点共有2种方法,而从B到C,一共3种方法,因此从A经过B到C的路径共2*3=6条。而从A到C的总方法数为(包括经过B和不经过B)C(5,2)=10,因为从A到C共走5个街区,其中3个往东,2个往北,相当于是从5个位置中选择2个位置安排向北,剩下3个安排向东。因此不经过B的路径共有10-6=4条,答案选A。
提醒:在计算排列组合的题目时,从反面考虑,用总数减去反面情况得到我们所要的结果,这种方法很常见。
2000-2024年AMC8真题和解析:2012年第19题

这道题的考点是代数(列方程解应用题)。
根据题意,假设红色玻璃球有x个,绿色玻璃球有y个,蓝色玻璃球有z个,因为“除了6个之外的其他玻璃球都是红色的”,所以绿色+蓝色=y+z=6。同理,我们可以得到x+z=8,x+y=4。把这3个方程相加,得到2(x+y+z)=18,因此x+y+z=9,答案选C。
这道题目要注意审题,有的考生直接将三个数字相加答案算到了18,结果发现没有答案。(如果有个选项是18,估计很多人会掉坑了)。
2000-2024年AMC8真题和解析:2011年第4题

这道题的考点是数据分析(中位数,众数和平均数)
我们把这些数按照升序排列为:0,0,1,1,2,2,3,3,3。根据定义:平均数=(0+0+1+1+2+2+3+3+3)/9=15/9,观察数列可得中位数为2,众数为3。因为15/9<2<3,所以答案为C。
提醒:这几个概念和算法要熟悉,尤其是数列个数是偶数的时候如何计算中位数。
欢迎联系我免费获得高清完整版的600道AMC8试题和解析,欢迎免费体验独家、精心设计的在线真题练习集。
六分成长针对AMC8的高质量、科学的备考资源,欢迎了解更多
上述六分成长独家制作的在线练习题,符合学习和认知心理学,来源于完整的历年AMC8真题,并且会持续更新。AMC8备考可用,反复练习,也有利于小学、初中数学能力提升。还有配套的系统学习文档、视频资料赠送。

相关文章:

高效备考2025年AMC8竞赛:吃透2000-2024年600道真题(免费送题)
我们继续来随机看五道AMC8的真题和解析,根据实践经验,对于想了解或者加AMC8美国数学竞赛的考生来说,吃透AMC8历年真题是备考更加科学、有效的方法之一。 最近有家长朋友问我,现在有哪些类似于奥数的比赛可以参加?我的…...

HTML5和CSS3新特性
Html新增属性 1.新增语义化标签 <header>:头部标签 <nav>:导航标签 <article>:内容标签 <section>:定义文档某个区域 <aside>:侧边栏标签 <footer>:尾部标签 2.…...

Java基础-正则表达式
文章目录 1.基本介绍2.正则底层实现1.matcher.find()完成的任务2.matcher.group(0)分析1.源代码2.解释(不分组)3.解释(分组) 3.总结 3.正则表达式语法1.基本介绍2.元字符的转义符号1.基本介绍2.代码实例 3.字符匹配符1.基本介绍2.…...

构建Pytorch虚拟环境教程
构建PyTorch虚拟环境通常涉及使用诸如Anaconda或venv等工具来管理Python环境,以便在一个独立的空间中安装PyTorch和其他依赖项。以下是使用Anaconda创建PyTorch虚拟环境的步骤(适用于不同操作系统,包括Windows、Linux和MacOS)&…...
uniapp页面嵌套其他页面的实现
功能: 类似于一个drawer,当主页面加载的时候会一并加载url对应的组件,当点击后以drawer形式显示组件里面的内容,可动画。 <navigator url"/pages/my/components/personalMessage" slot"right"><view><di…...

XUbuntu22.04之安装Plantuml(二百二十三)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...

第四周刷题小结
第一天 P1068 [NOIP2009 普及组] 分数线划定 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 思路: 这个题感觉不难,主要是用到了结构体cmp的自定义排序,但是还是错了一次,就是没注意到题目给的条件。 #include<iostream&g…...
基于Java中的SSM框架实现考研指导平台系统项目【项目源码+论文说明】
基于Java中的SSM框架实现考研指导平台系统演示 摘要 应对考研的学生,为了更好的使校园考研有一个更好的环境好好的学习,建议一个好的校园网站,是非常有必要的。提供学生的学习提供一个交流的空间。帮助同学们在学习高数、学习设计、学习统计…...

项目2-用户登录
1.创建项目 2.引入前端代码并检查是否有误 3.定义接口 需求分析 对于后端开发⼈员⽽⾔, 不涉及前端⻚⾯的展⽰, 只需要提供两个功能 1. 登录⻚⾯: 通过账号和密码, 校验输⼊的账号密码是否正确, 并告知前端 2. ⾸⻚: 告知前端当前登录⽤⼾. 如果当前已有⽤⼾登录, 返回登录的账…...

网易web安全工程师进阶版课程
课程介绍 《Web安全工程师(进阶)》是由“ i春秋学院联合网易安全部”出品,资深讲师团队通过精炼的教学内容、丰富的实际场景及综合项目实战,帮助学员纵向提升技能,横向拓宽视野,牢靠掌握Web安全工程师核心…...
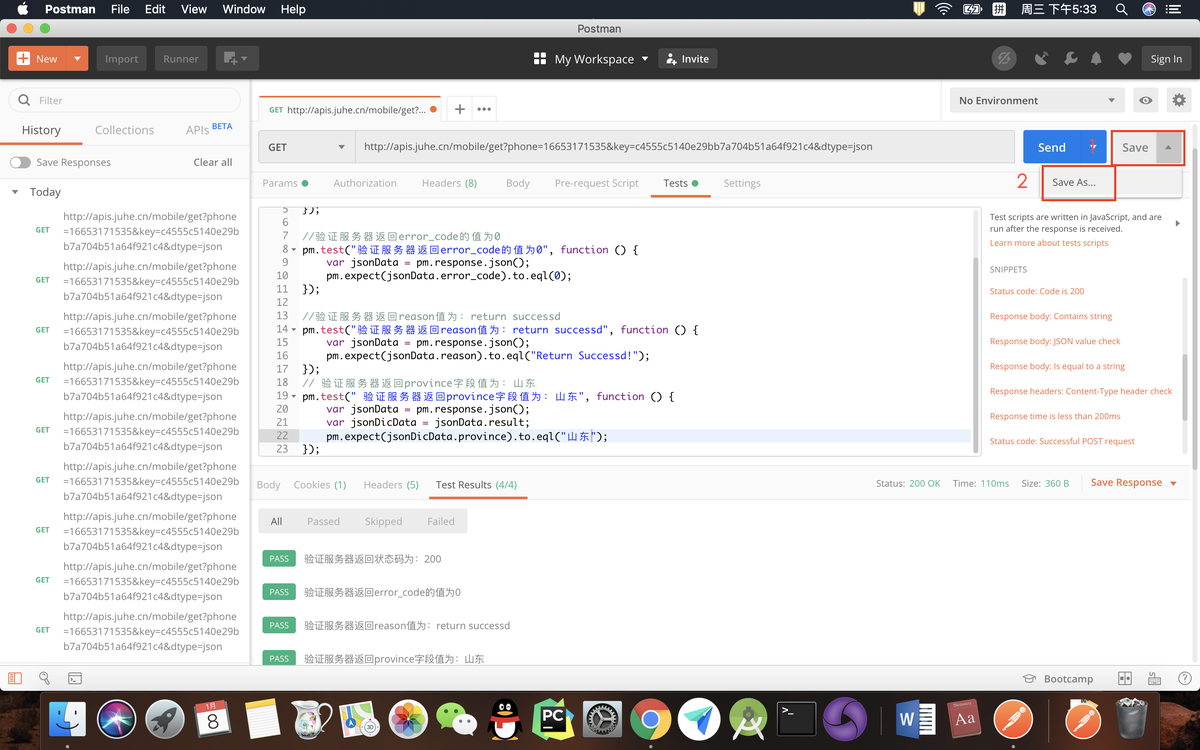
【Postman】工具使用介绍
一、postman工具介绍 1.什么是postman postman是谷歌开发的一款网页调试和接口测试工具,能够发送任何请求类型的http请求,支持GET/POST/PUT/DELETE等方法。postman简单易用,可以直接填写URL,header,body就可以发送一…...
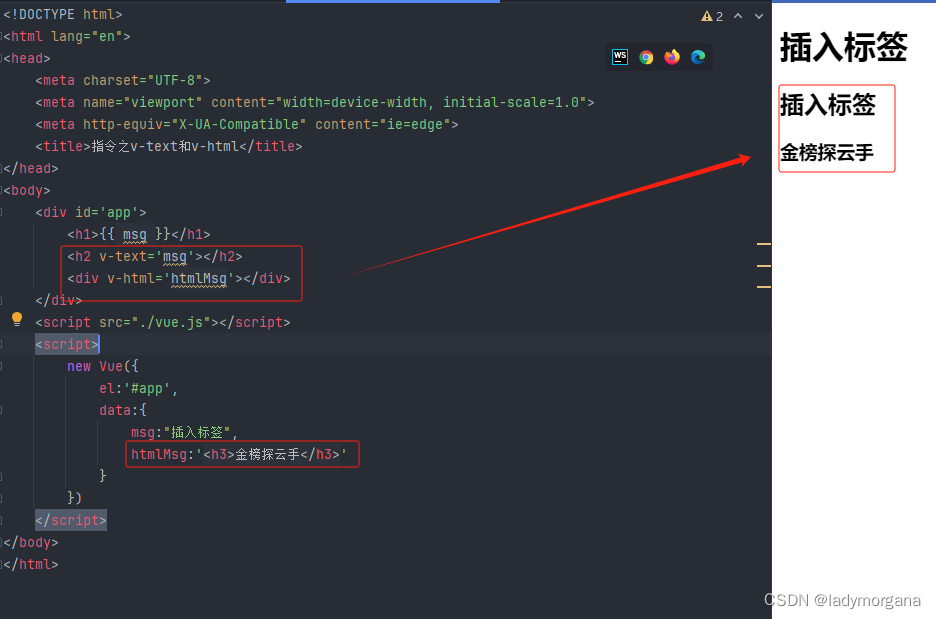
【vue核心技术实战精讲】1.3 - 1.6 VUE 指令 (上)
前言 上节,我们学习了 Vue的起步 和 插值表达式 本节内容 Vue指令之v-text 和 v-htmlVue指令之v-if 和 v-showVue指令之v-bind绑定Vue指令之v-on事件处理 1、v-text 和 v-html {{}} 和v-text的作用是一样的 都是插入值,直接渲染 ≈ innerTextv-html既能插入值 又能插入标签…...
vscode使用Runner插件将.exe文件统一放到一个目录下
找到右下角管理,点击扩展。 找到Code Runner插件,打开扩展设置。 向下翻,找到Executor Map,点击在settings.json中编辑。 在c和c的配置命令栏中增加\\\output\\即可。(增加的目录不能自动创建,需要手动创建…...

[commonjs--resolver] Missing “./jsx-runtime.js“ specifier in “react“ package
修复vite构建时错误 vite打包,第三方包引用的react版本不一致问题修复(不是最优解) // vite.config.js import { defineConfig } from vite; import react from vitejs/plugin-react; import path from path;export default defineConfig({plugins: [react(), // 如果使用Rea…...
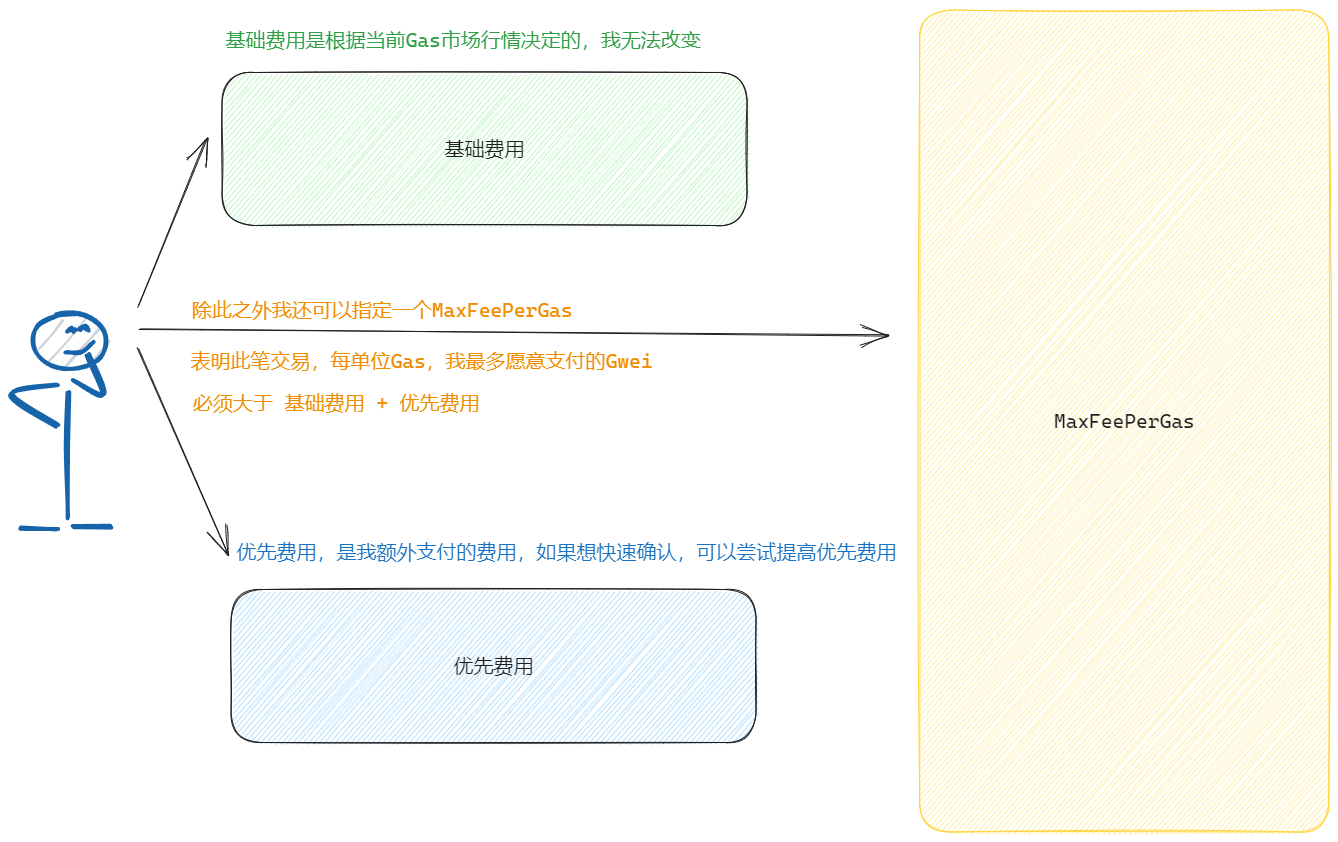
ETH Gas 之 Base Fee Priority Fee
前情回顾 ETH网络 之 Gas EIP-1559 EIP-1559 EIP-1559是以太坊改进提案(Ethereum Improvement Proposal),旨在改进以太坊的交易费用机制。该提案引入了一种新的交易费用模型,以提高交易费用的可预测性和网络的效率。我们本文各…...

【小白入门篇1】GPT到底是怎样练成?
由于具有代表性的OpenAI公司GPT模型并没有开源,所以本章节是参考一些开源和现有课程(李宏毅)讲解ChatGPT原理。本章没有涉及到很多数学运算,比较适合小白了解GPT到底是怎么练成。GPT的三个英文字母分别代表Generative(生成式)&…...

Django——forms组件
Django——forms组件 forms组件:通过后端在Django中定义forms类,可以在 html 中动态的生成一个表单;检验用户提交的数据。 在应用中创建一个名为 :forms 的py文件 # 导入 forms 组件 from django import forms# 自定义 forms …...

利用K8S Statefulset搭建Etcd集群 - PVC存储
概述 在测试过程中发现,直接使用本地存储,当节点机器损坏了,对应机器的etcd数据也丢失了,故而做了利用K8S PV,PVC以及NFS来存储数据的尝试,经过一番折腾,测试成功,博文记录…...
手撕算法-接雨水
描述 分析 i位置能积累的雨水量,等于其左右两边最大高度的最小值。为了能获取i位置左右两边的最大高度。使用动态规划。两个dp数组: leftMaxrightMax 其中 leftMax[i] 代表i位置左边的最大高度rightMax[i] 代表i位置右边的最大高度 初始状态&#x…...

探索AI大模型学习:理论基础、技术突破与未来挑战
在当今技术飞速发展的时代,人工智能(AI)大模型学习无疑是推动科技进步和创新的关键力量。AI大模型学习的核心在于通过训练大规模的数据集来提升模型的性能,使之能够更准确、更高效地完成各种任务,从而在多个领域中实现…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...
