探索AI大模型学习:理论基础、技术突破与未来挑战
在当今技术飞速发展的时代,人工智能(AI)大模型学习无疑是推动科技进步和创新的关键力量。AI大模型学习的核心在于通过训练大规模的数据集来提升模型的性能,使之能够更准确、更高效地完成各种任务,从而在多个领域中实现突破性的进展。这一过程不仅要求研究人员拥有扎实的数学基础和编程技能,还需要他们对应用领域的业务场景有深入的理解。本文将探讨AI大模型学习的理论基础,包括其数学基础、算法原理以及模型架构设计等方面,同时分析各种经典深度学习模型在处理大规模数据中的优势与挑战。
AI大模型学习的数学基础
AI大模型学习的理论基础建立在复杂的数学理论之上,包括但不限于线性代数、概率论、统计学以及优化理论等。这些数学工具为研究人员提供了一种强大的语言,用于描述和分析模型的行为。例如,线性代数中的矩阵运算在卷积神经网络(CNN)的前向传播和反向传播过程中发挥着核心作用;概率论和统计学则是理解和设计基于概率的模型参数估计方法,如最大似然估计和贝叶斯推断,的基础。
算法原理与模型架构设计
AI大模型学习的发展历程中,各种深度学习模型的提出标志着关键的技术突破。卷积神经网络(CNN)通过其特有的卷积层处理图像数据,能够有效识别和提取图像中的局部特征。循环神经网络(RNN)和其变体如长短期记忆网络(LSTM)则在处理序列数据,如文本和时间序列,方面展示出独特的优势。Transformer模型,则通过自注意力机制(Self-Attention),极大地提高了处理长距离依赖问题的能力,成为了自然语言处理(NLP)等领域的主流模型。
优势与挑战
尽管AI大模型学习在多个领域中都展现出了巨大的潜力,但它们仍面临诸多挑战。首先,大规模数据的处理和模型的训练需要巨大的计算资源,这对研究人员和开发者是一大负担。此外,模型的可解释性也是一个重要的研究方向,对于增强用户的信任和接受度至关重要。最后,数据的质量和多样性也对模型的性能有着直接影响,如何获取和处理高质量的数据成为了提升模型性能的关键。
结语
AI大模型学习正处于快速发展之中,它不仅要求研究者具备深厚的数学基础和强大的编程能力,还需要他们对特定领域有深入的理解。通过不断优化模型结构和算法,AI大模型学习有望在未来继续提升其准确性和效率,为人类社
相关文章:

探索AI大模型学习:理论基础、技术突破与未来挑战
在当今技术飞速发展的时代,人工智能(AI)大模型学习无疑是推动科技进步和创新的关键力量。AI大模型学习的核心在于通过训练大规模的数据集来提升模型的性能,使之能够更准确、更高效地完成各种任务,从而在多个领域中实现…...
Linux:点命令source
相关阅读 Linuxhttps://blog.csdn.net/weixin_45791458/category_12234591.html?spm1001.2014.3001.5482 source命令用于读取一个文件的内容并在当前Shell环境(包括交互式Shell或是非交互式Shell)执行里面的命令。它被称为点命令是因为命令名source也可…...

iOS开发 - 转源码 - __weak问题解决
iOS开发 - 转源码 - __weak问题解决 在使用clang转换OC为C代码时,可能会遇到以下问题 cannot create __weak reference in file using manual reference 原因 __weak弱引用是需要runtime支持的,如果我们还只是使用静态编译,是无法正常转换的…...

【Linux基础】dash和bash简介
Dash(Debian Almquist Shell)和 Bash(Bourne Again Shell)是 Unix/Linux 系统中的命令行 shell,用于执行命令、管理文件系统、编写脚本等任务的工具。 一、Dash和Bash的区别: Bash(Bourne Agai…...

精读《如何做好 CodeReview》
1 引言 任何软件都是协同开发的,所以 CodeReview 非常重要,它可以帮助你减少代码质量问题,提高开发效率,提升稳定性,同时还能保证软件架构的稳定性,防止代码结构被恶意破坏导致难以维护。 所以 CodeRevie…...
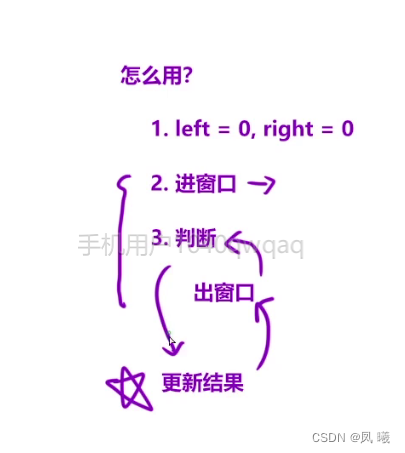
双指针(滑动窗口)-算法刷题
一.移动零(. - 力扣(LeetCode)) 算法思想 : 设置两个指针left,right,将数组分为三块[0,left]为不为0的元素,[left1,right-1]为0元素,[right,num.size()-1]为未扫描的区域,…...
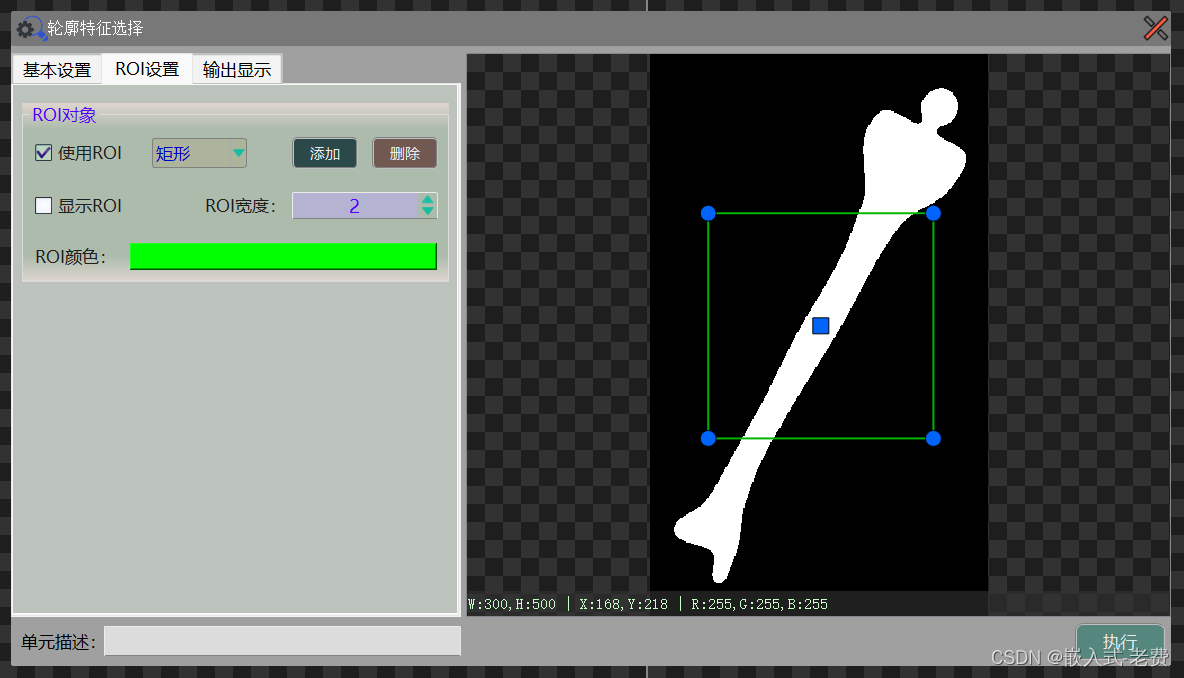
上位机图像处理和嵌入式模块部署(qmacvisual之ROI设定)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 ROI,全称是region of interest,也就是感兴趣区域。这里面一般分成两种情况,一种是所有的算法都依赖于这个ROI&a…...

银行监管报送系统介绍(五):金融统计数据大集中自动化报送系统——PBOC Report
人民银行金融统计数据大集中自动化报送系统(简称PBOC Report),是基于现代计算机网络技术应用基础上,由人行总行设置金融统计数据服务器,建立的一个全国统一的金融统计数据库。 人行针对各银行存贷款、中间业务、网点人…...
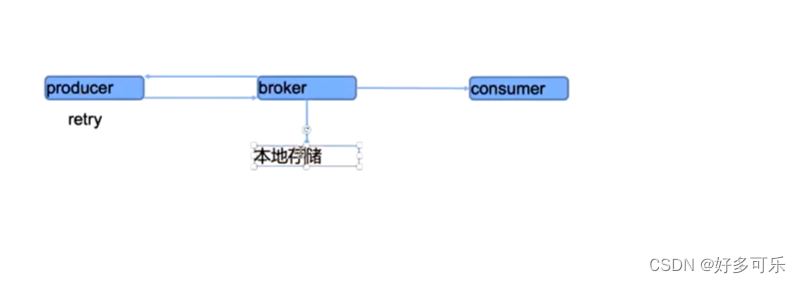
常用中间件redis,kafka及其测试方法
常用消息中间件及其测试方法 一、中间件的使用场景引入中间件的目的一般有两个:1、提升性能常用的中间件:1) 高速缓存:redis2) 全文检索:ES3) 存日志:ELK架构4) 流量削峰:kafka 2、提升可用性产品架构中高可…...
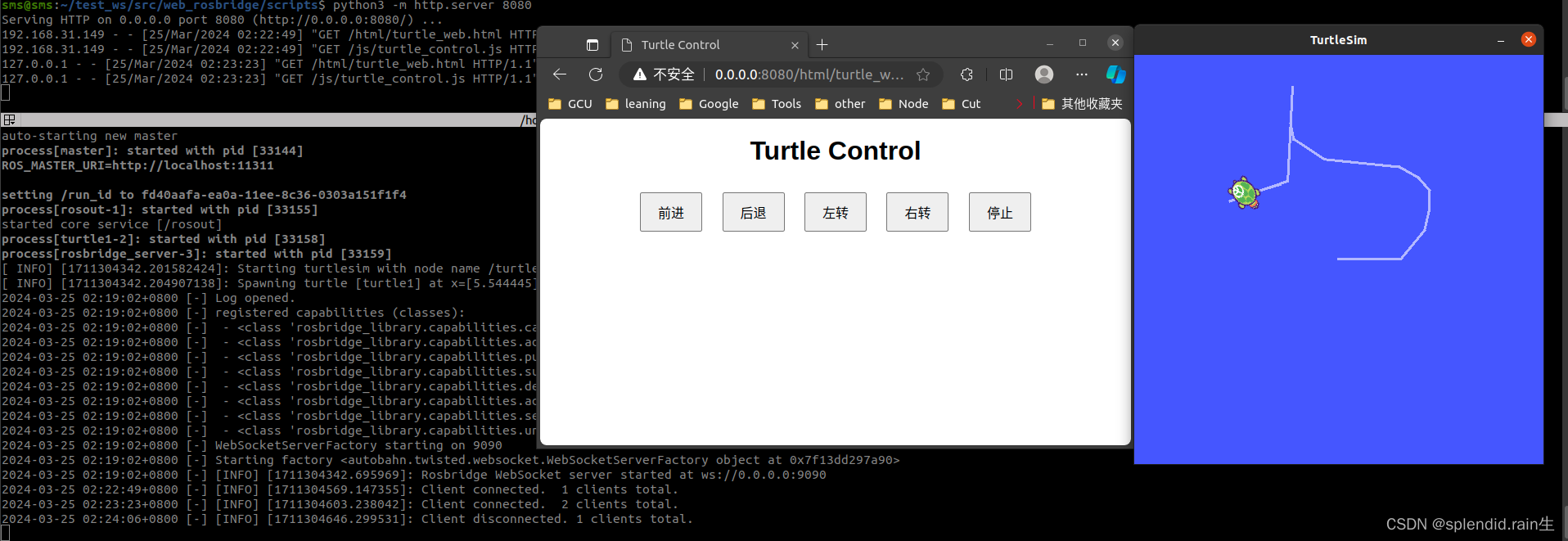
ROS1通过rosbridge在局域网中控制turtle进行运动(PC和手机)
通过ROSbridge控制小海龟(turtlesim)的具体案例。使用一个简单的Python脚本通过通过局域网上连接上传ROSbridge服务器,并发送速度指令来控制小海龟的移动 功能包的结构如下: HTML文件的编写(界面) html用…...

MQ高级篇---消息可靠性
MQ的一些常见问题 后面内容基于springboot 2.3.9.RELEASE 消息可靠性 生产者确认机制 在publisher微服务中application.yml中添加 spring:rabbitmq:publisher-confirm-type: correlatedpublisher-returns: truetemplate:mandatory: true每个RabbitTemplate只能配置一个Return…...

SpringMVC | SpringMVC中的 “文件上传和下载”
目录: 一、文件上传1.1 文件上传“概述”1.2 文件上传“具体配置” :“前端”中配置“文件上传” ( type“file” 满足3个条件 )“后端”中配置“文件上传” ( 配置id为“CommonsMultipartResolver”的bean 配置“文件上传”的“约束条件” 通过“MultipartFile接口”参数接…...
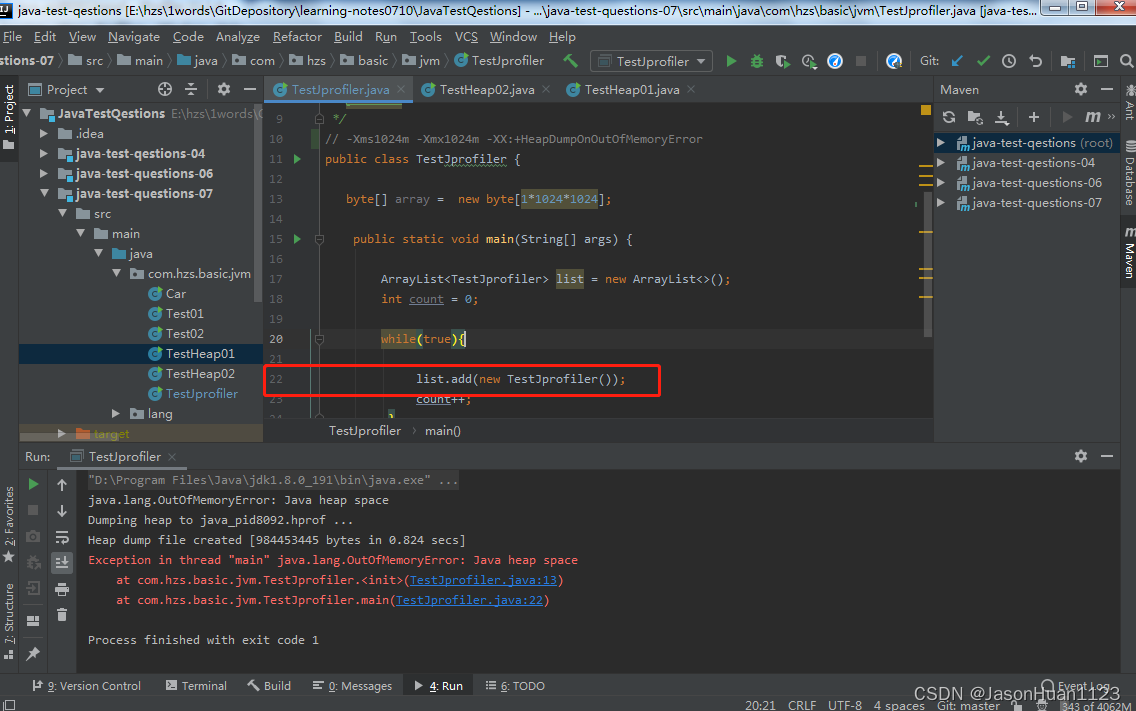
JVM快速入门(2)HotSpot和堆、新生区、永久区、堆内存调优、JProfiler工具分析OOM原因、GC(垃圾回收)、JVM经典面试笔试题整理
5.6 HotSpot和堆 5.6.1 Hotspot 三种JVM: Sun公司,HotspotBEA,JRockitIBM,J9 VM,号称是世界上最快的Java虚拟机 我们一般学习的是:HotSpot 5.6.2 堆 Heap,一个JVM只有一个堆内存,…...
我的风采——android studio
目录 实现“我的风采”页面要求理论代码生成apk文件 实现“我的风采”页面 要求 要求利用’java框架的边框布局实现“找的风采 ”页而,其中中间为你的生活照,左右和下面为按钮,上面为标签 理论 Java GUI编程是Java程序设计的重要组成部分…...
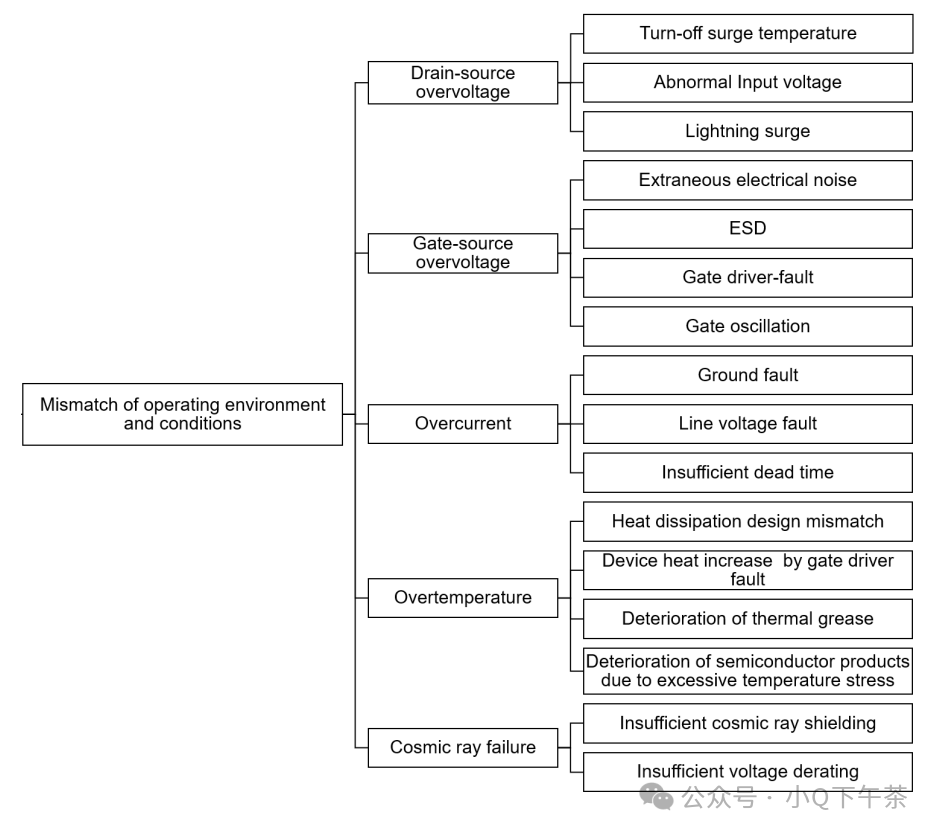
BMS设计中的短路保护和MOSFET选型(上)
电池管理系统(BMS)是一种能够对电池进行监控和管理的电子装备,是电池与用户之间的纽带。通过对电压、电流、温度以及SOC等数据采集,计算进而控制电池的充放电过程,主要就是为了能够提高电池的利用率,防止电…...
)
用go实现一个任务调度类 (泛型)
用go实现一个任务调度类 (泛型) 源码地址: https://github.com/robinfoxnan/BirdTalkServer/blob/main/server/core/workmanager.go 1.概述 实现了一个简单的任务管理系统,允许用户定义任务和工作者,并将任务分配给…...

ansible 管理工具以及常用模块
一、前期准备 1、安装 yum install ansible 如果yum源没有ansible,需要提前配置yum源: mv /etc/yum.repos.d/epel.repo /etc/yum.repos.d/epel.repo.backup mv /etc/yum.repos.d/epel-testing.repo /etc/yum.repos.d/epel-testing.repo.backup wget -O…...
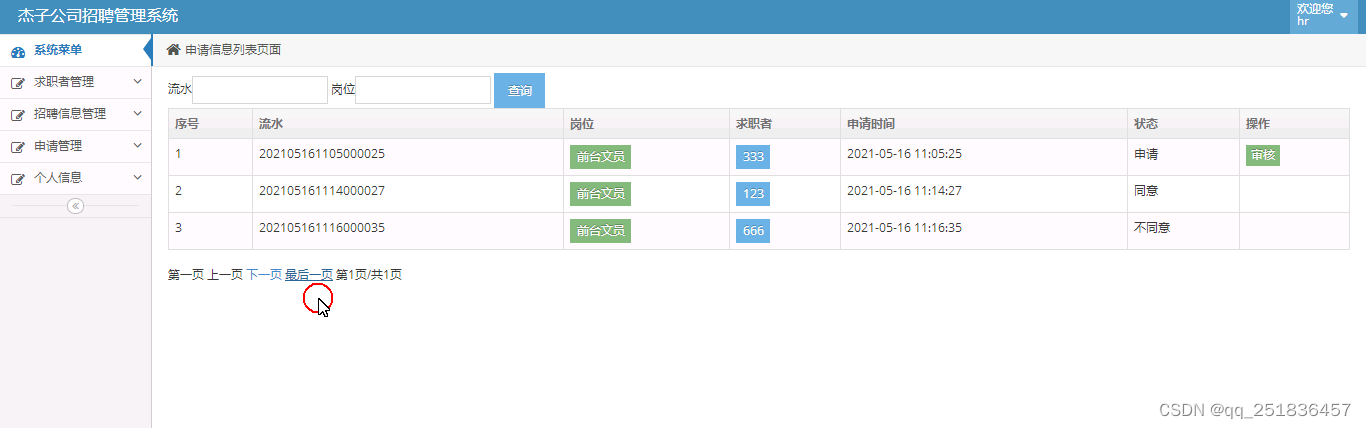
javaSSM公司招聘管理系统IDEA开发mysql数据库web结构计算机java编程maven项目
一、源码特点 IDEA开发SSM公司招聘管理系统是一套完善的完整企业内部系统,结合SSM框架和bootstrap完成本系统,对理解JSP java编程开发语言有帮助系统采用SSM框架(MVC模式开发)MAVEN方式加 载,系统具有完整的源代码和…...

蓝桥杯day11刷题日记
P8615 [蓝桥杯 2014 国 C] 拼接平方数 思路:先把数据范围内的平方数打上标记,然后就是遍历这个区间,转成字符串(好拆数据),用substr拆开数据,再强转成整数类型,最后查看拆开的数据是…...
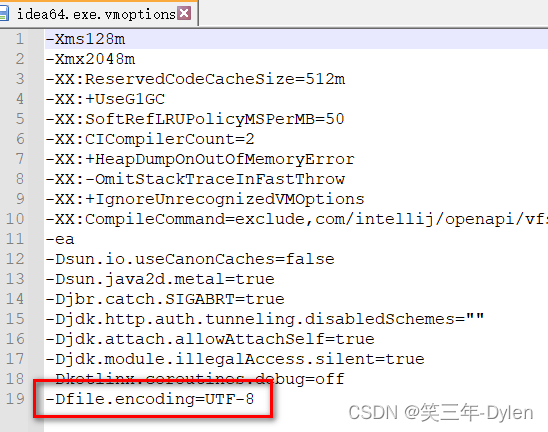
IDEA, Pycharm, Goland控制台乱码
IDEA, Pycharm, Goland控制台乱码 问题描述: 控制台出现����等乱码 复现频率: 总是 解决方案: 以IDEA为例 添加 -Dfile.encodingUTF-8位置 idea64.exe.vmoptions 在安装idea的bin目录idea.vmoptions idea客户端 示意图...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
