动态规划Dynamic Programming

上篇文章我们简单入门了动态规划(一般都是简单的上楼梯,分析数据等问题)点我跳转,今天给大家带来的是路径问题,相对于上一篇在一维中摸爬滚打,这次就要上升到二维解决问题,但都用的是动态规划思想嘛,所以大差不差,且听我慢慢道来。
还是用一样的方法,用同样的分析思路和技巧来分析问题解决问题。
路径规划
不同路径

- 状态表示
这道题我们需要知道的是从左上角位置走到右下角位置总共有多少的路径,我们可以将问题拆分,题目中所说,机器人每次只能向下或者向右移动一步,所以我们到达右下角位置是怎么到达的呢?
如图
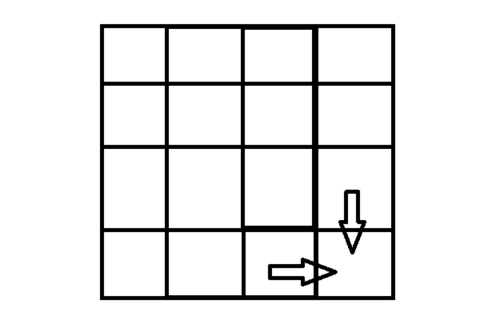 所以到达目标的方法就是到达这两个位置方法的总和。
所以到达目标的方法就是到达这两个位置方法的总和。
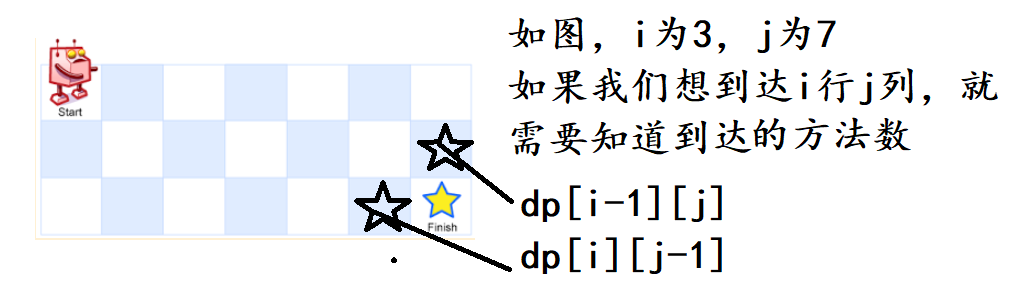
因此这道题的状态表示就是到达ij位置总共的方法数。 - 状态转移方程
有了上边的分析,我们可以很清晰地知道
状态转移方程为
dp[i][j]=dp[i-1][j]+dp[i][j-1]
- 初始化
初始化顺序即填表顺序是从左上角到右下角,但是我们应该怎么初始化呢?如果套用我们的状态转移方程,我们会发现在数租的边缘部分一定会遇到越界的情况。

所以在初始化时,我们可以将数组多开一行一列,这样就可以解决越界访问的问题,如何初始化这个表格呢?我们来试着分析。

其他位置全部初始化为0,这样就可以避免多开的数组影响我们后续的得到的结果。 - 填表顺序
填表顺序就是从左上角向左下角进行填写。 - 返回值
很简单,就是返回填表后到达i,j位置时的值即可
接下来我们就可以根据分析出的结论写代码了。
class Solution {
public:int uniquePaths(int m, int n) {//new出一个二维数组,并将他们的值初始化为0vector<vector<int>> dp(m+1,vector<int>(n+1));//这里应该怎么给空间啊dp[0][1]=1;for(int i=1;i<=m;i++)//先填每一行for(int j=1;j<=n;j++)//再填每一列 dp[i][j]=dp[i-1][j]+dp[i][j-1];return dp[m][n];}
};
这里还有一道十分相仿的题目,多了一步扩展的思维而已,尝试一下吧!
不同路径2
第二道题
珠宝的最高价值

如果说上一道题对标的是上一篇中的上楼梯的方法数,那么这道题对标的就是上楼梯最小花费。
思路和上一道题目很像,一起来看一看。
- 状态表示
同样要创建一个二维数组,到达ij位置可以拿到的珠宝价值最高,那么状态表示就是到达ij位置能拿到的最大珠宝价值,说白了就是所以路径中求和最大的一条路径。 - 状态转移方程
移动方式和上一道题目一样,但是相比于上一道题目的相加,这道题目就是从上边或者左边到达ij位置时,他们两个谁的路径和最大。因为上一道题目已经解释很清楚了,这里就不再画图赘述。
dp[i][j]=max(dp[i-1][j],dp[i][j-1];
- 填表顺序
从左上角向右下角。要注意是从下表为1,1位置开始填表的。 - 初始化
初始化方式和前边那道题目大同小异,只不过我们多开的数组默认为0不用管就行,因为第一个位置只需要加上他这个位置的财宝价值即可。 - 返回值
返回到达左下角位置能达到的最高价值数。
我们还是直接来展示代码吧,毕竟和前边那道题很像,除了状态转移方程不同。
代码如下
class Solution {
public:int jewelleryValue(vector<vector<int>>& frame) {int m=frame.size();int n=frame[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i=1;i<=m;i++)for(int j=1;j<=n;j++)dp[i][j]=max(dp[i][j-1],dp[i-1][j])+frame[i-1][j-1];return dp[m][n];}
};
第三道题
下降路径最小和

首先来进行题目解析,这道题目只需要从上到下找到最小的路径即可,而且在某位置可以向下边三个位置进行跳转。
- 状态表示
状态表示就是到达ij位置时,需要的最小路径和,然后找出最后一行中最小的,就找到了最小路径下降和。 - 状态转移方程
可以来画图分析一下
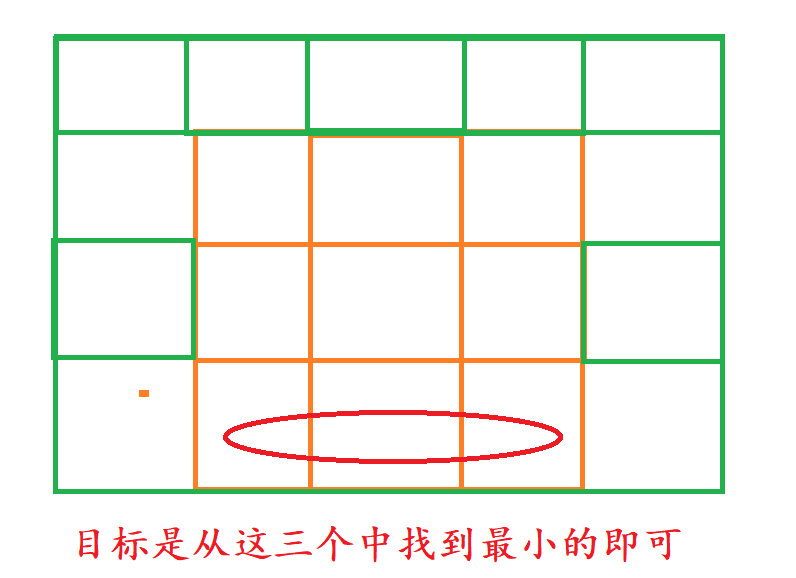
根据我们的状态表示,我们需要找到最小路径和,只需要找到这个位置上边三种情况的最小路径和即可。
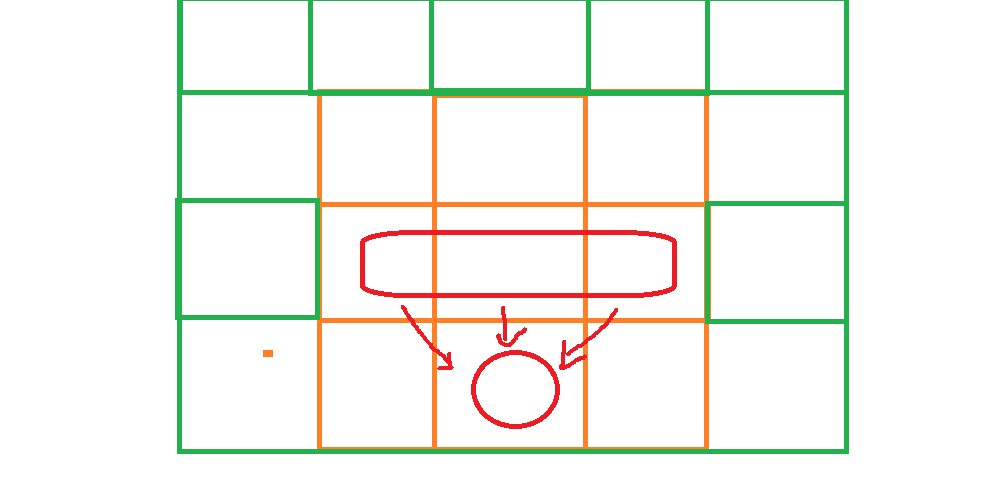
当然,到达ij位置时,还需要加上ij位置上的值。
故而状态转移方程为
dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j+1],dp[i-1][j]))+matrix[i-1][j-1];//要注意这里位置的对应
这里状态对应的问题后边会解释到。
-
初始化
这里初始化是一个问题,问题在于在我们求第一行时,第一行的上边并没有数据,访问dp[-1][-1]势必会造成越界访问,如何解决呢?有了上边题目的铺垫,只需要扩展数组即可。
相信大家已经看到了上边的画图中分别用两种颜色标记,如何初始化才能不影响后续的结果呢?
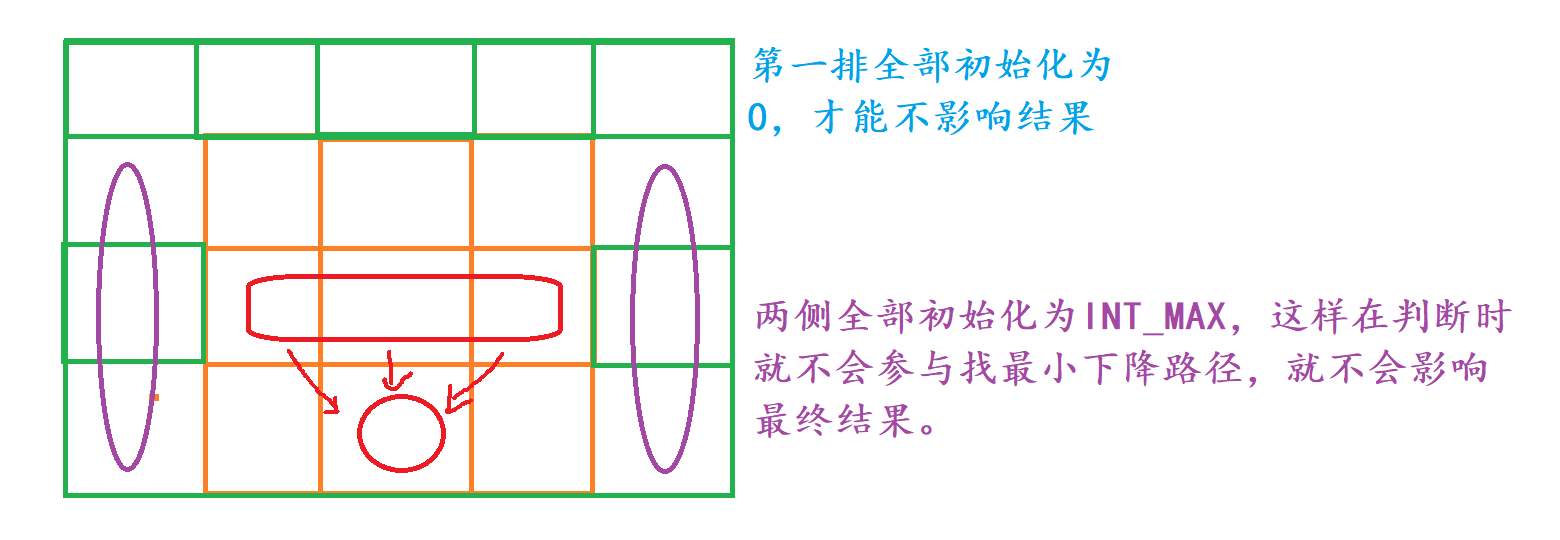
因为这道题目的数组开的并不规则,所以对应位置容易混淆,如果你匆匆写代码的话,势必会出现这样的问题,

还会出现这样的问题
第一种就是没有空控制好dp表的填写,导致初始化时的INT_MAX参与了运算,第二种就是因为多开两列,多开一行导致的位置判断不准确,以至于越界访问了。 -
填表顺序
很明显,从上往下进行填表 -
返回值
这里返回值和之前不太一样,需要找到最后一行元素中最小的一个,然后返回即可。
代码如下,一定要尝试自己写一下,这道题是正方形表格,但是我作为长方形表格来做了,大家可以忽略这些小细节哈。
class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int m=matrix.size();int n=matrix[0].size();vector<vector<int>> dp(m+1,vector<int> (n+2,INT_MAX));//怎么把两边初始化为int_max;//cout<<int_max;for(int k=0;k<=n+1;k++){dp[0][k]=0;}for(int i=1;i<=m;i++){for(int j=1;j<=n+1;j++)//这里要注意,只需要初始化我们需要的部分{dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j+1],dp[i-1][j]))+matrix[i-1][j-1];//要注意这里位置的对应}}//此时只需找到最后一行的最小值。int ret=INT_MAX;for(int j=1;j<=n;j++){ret=min(ret,dp[m][j]);}return ret;}
};
本文到此结束,感谢大家观看,有问题及时提出,我会积极解决的。
相关文章:

动态规划Dynamic Programming
上篇文章我们简单入门了动态规划(一般都是简单的上楼梯,分析数据等问题)点我跳转,今天给大家带来的是路径问题,相对于上一篇在一维中摸爬滚打,这次就要上升到二维解决问题,但都用的是动态规划思…...

详解机器学习概念、算法
目录 前言 一、常见的机器学习算法 二、监督学习和非监督学习 三、常见的机器学习概念解释 四、深度学习与机器学习的区别 基于Python 和 TensorFlow 深度学习框架实现简单的多层感知机(MLP)神经网络的示例代码: 欢迎三连哦! 前言…...
语音转文字——sherpa ncnn语音识别离线部署C++实现
简介 Sherpa是一个中文语音识别的项目,使用了PyTorch 进行语音识别模型的训练,然后训练好的模型导出成 torchscript 格式,以便在 C 环境中进行推理。尽管 PyTorch 在 CPU 和 GPU 上有良好的支持,但它可能对资源的要求较高&#x…...
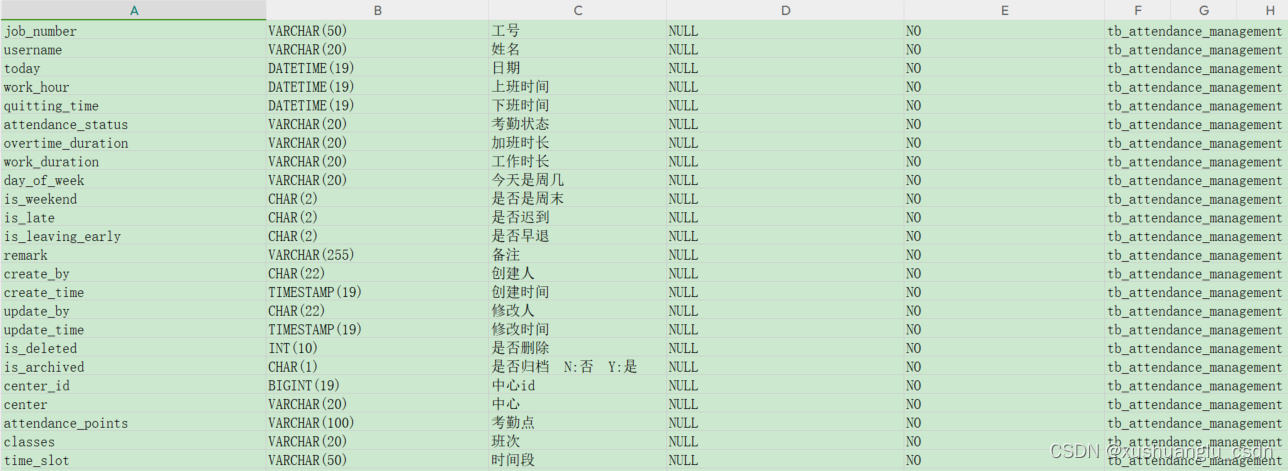
第1篇:Mysql数据库表结构导出字段到Excel(一个sheet中)
package com.xx.util;import org.apache.poi.ss.usermodel.*; import org.apache.poi.xssf.usermodel.XSSFWorkbook;import java.sql.*; import java.io.*;public class DatabaseToExcel {public static void main(String[] args) throws Exception {// 数据库连接配置String u…...

Request请求参数----中文乱码问题
一: GET POST获取请求参数: 在处理为什么会出现中文乱码的情况之前, 首先我们要直到GET 以及 POST两种获取请求参数的不同 1>POST POST获取请求参数是通过输入流getReader来进行获取的, 通过字符输入流来获取响应的请求参数, 并且在解码的时候, 默认的情况是 ISO_885…...

labelImg安装方法
labelImg安装方法(简单方法) - 知乎 (zhihu.com) 1. lableImg下载 git clone https://github.com/tzutalin/labelImg.git 2. 制作lableImg所需的"condapython"环境(conda需要先安装,最好再设置下下载源) 打开Anaconda Prompt对话框 # 创建环境 conda create -n …...
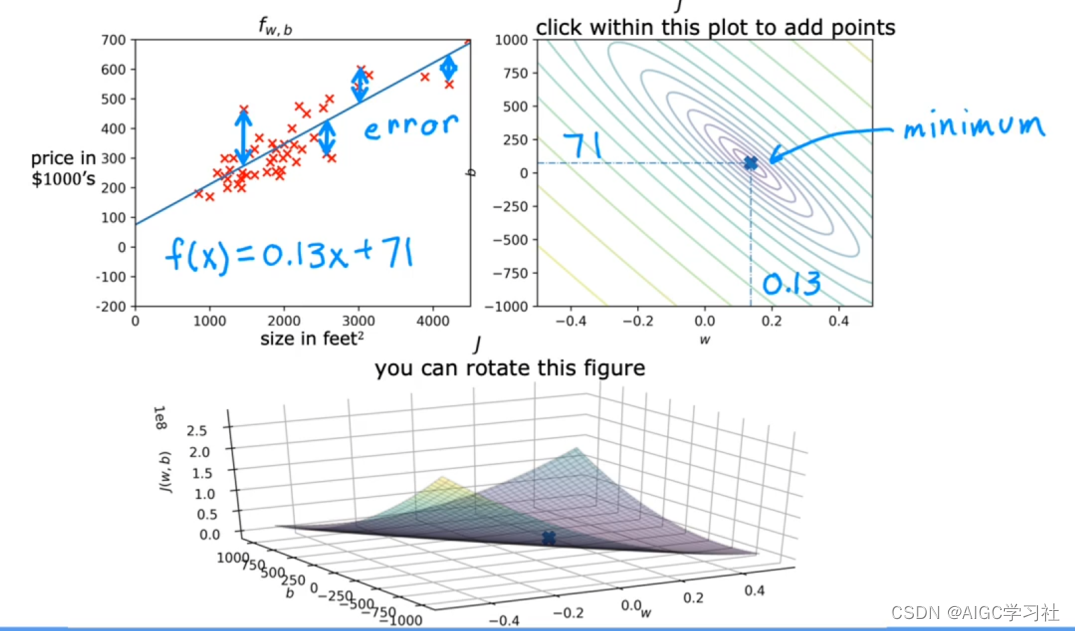
吴恩达2022机器学习专项课程(一) 3.6 可视化样例
问题预览 1.本节课主要讲的是什么? 2.不同的w和b,如何影响线性回归和等高线图? 3.一般用哪种方式,可以找到最佳的w和b? 解读 1.课程内容 设置不同的w和b,观察模型拟合数据,成本函数J的等高线…...

C#入门及进阶教程|Windows窗体属性及方法
1.Windows窗体 窗体本身是一个对象,对应于System.Windows.Forms名称空间的Form类。它有自己的属性、方法和事件,用于控制窗体的外观和行为。窗体又是各种控件的容器,用于容纳各种窗体控件。如果想生成窗体,必须从Form类派生出自己…...
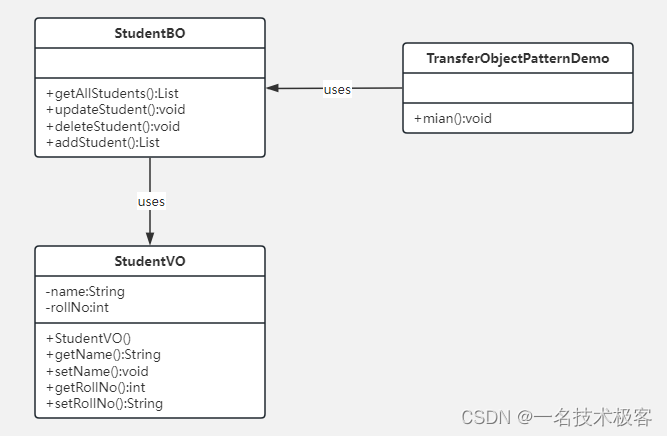
34-Java传输对象模式 ( Transfer Object Pattern )
Java传输对象模式 实现范例 传输对象模式(Transfer Object Pattern)用于从客户端向服务器一次性传递带有多个属性的数据传输对象也被称为数值对象,没有任何行为传输对象是一个具有 getter/setter 方法的简单的 POJO 类,它是可序列…...
flutter实现视频播放器,可根据指定视频地址播放、设置声音,进度条拖动,下载等
需要装依赖: gallery_saver: ^2.3.2video_player: ^2.8.3 AndroidManifest.xml <uses-permission android:name"android.permission.INTERNET"/> 实现代码 import dart:async; import dart:io;import package:flutter/material.dart; import pa…...

微服务(基础篇-001-介绍、Eureka)
目录 认识微服务(1) 服务架构演变(1.1) 单体架构(1.1.1) 分布式架构(1.1.2) 微服务(1.1.3) 微服务结构 微服务技术对比 企业需求 SpringCloud(1.2) …...
mac 解决随机出现的蓝色框
macbookair为什么打字的时候按空格键会出现蓝色框? - 知乎...

深入理解与使用go之函数与方法--使用
深入理解与使用go之函数与方法–理解与使用 文章目录 引子函数与方法分类函数函数入参普通参数可变参数默认值返回命名不带命名带命名讨论init 函数defer 函数方法值接收指针接收构造函数引子 在 Go 语言中,函数被视为一等公民(First-Class Citizens),这意味着函数可以像其…...

【QT问题】 Qt信号函数如果重名,调用怎么处理
问题描述: 在调用某个类的信号函数的时候,出现信号函数名字相同,参数不同的情况,但是Qt在链接信号槽的时候,又不需要指明信号函数参数,此时就会出现无法分辨的情况。 例如:QComboBox的信号 Q_…...
)
登山小分队(dfs,模拟)
原题链接: 题目描述 Foxity和他的好友们相约去爬山,但是他们每个人都来到了不同的山脚下。整个山的结构类似一棵 "树",有很多的观光节点通过一条条山道连接起来。 在图论中,树是一种无向图,其中任意两个顶…...

Luminar Neo:重塑图像编辑新纪元,Mac与Win双平台畅享创意之旅
在数字时代的浪潮中,图像编辑软件已成为摄影师和设计师们不可或缺的创作工具。Luminar Neo,作为一款专为Mac与Windows双平台打造的图像编辑软件,正以其卓越的性能和创新的编辑功能,引领着图像编辑的新潮流。 Luminar Neo不仅继承…...

计算机二级Python题库深度解析与备考策略
计算机二级Python题库深度解析与备考策略 随着信息技术的飞速发展,Python作为一门简洁、易读且功能强大的编程语言,受到了越来越多人的青睐。计算机二级Python考试作为衡量考生Python编程水平的重要标准,其题库内容涵盖了Python语言的基础知…...
微信商家转账到零钱:实用指南,涵盖开通、使用与常见问题
商家转账到零钱是什么? 商家转账到零钱功能整合了企业付款到零钱和批量转账到零钱,支持批量对外转账,操作便捷。如果你的应用场景是单付款,体验感和企业付款到零钱基本没差别。 商家转账到零钱的使用场景有哪些? 这…...

[精选]Kimi到底是什么,将带来什么?
## 阿里通义千问重磅升级:免费开放1000万字长文档处理功能。 Kimi突然的泼天富贵,大家都想沾一把。短期这一块大概率会继续热一段时间。 作为月之暗面的创始人,杨植麟常把他的AGI梦想形容为“登月计划”,长文本就是这个伟大计划…...

MySQL学习笔记------SQL(2)
ziduanSQL DML 全称为:Data Manipulation Language,用来对数据库中表的数据记录进行增删改操作 插入数据 添加数据(INSERT) 给指定字段添加数据:INSERT INTO 表名(字段名1,字段名2,......…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
