数据结构·排序
1. 排序的概念及运用
1.1 排序的概念
排序:排序是将一组“无序”的记录序列,按照某个或某些关键字的大小,递增或递减归零调整为“有序”的记录序列的操作
稳定性:假定在待排序的记录序列中,存在多个具有相同关键字的记录,若经过排序,这些记录的相对次序保持不变。及在原序列中, r[i] = r[j],且 r[i] 在 r[j] 之前,而在排序后的序列中,r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的
内部排序:数据元素全部放在内存中的排序
外部排序:数据元素太多,不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序
1.2 常见的排序算法
插入排序:直接插入排序,希尔排序
选择排序:选择排序,堆排序
交换排序:冒泡排序,快速排序
归并排序:归并排序
2. 常见排序算法的实现
2.1 插入排序
基本思想:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列,这个过程就像我们在整理扑克牌一样
2.1.1 直接插入排序 O(N^2)
当插入第 i (i >= 1) 个元素时,前面的 array[0],array[1] …… array[i-1] 已经排好序,此时用 array[i] 的排序码与 array[i-1],array[i-2],…… 的排序码顺序进行比较,找到插入为止及将 array[i-1] 插入,原来位置上的元素顺序后移
实现:
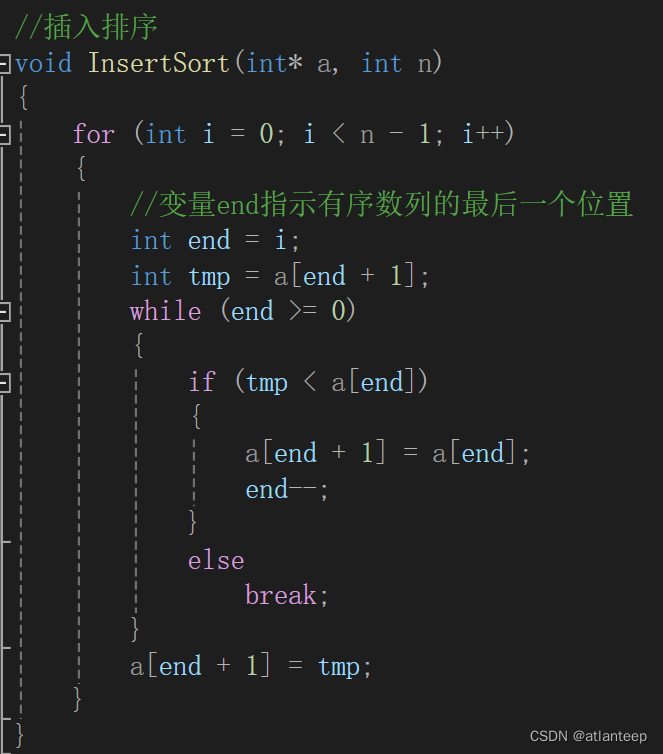
直接插入排序的特性总结
1. 元素集合越接近有序,直接插入算法的时间效率越高
2. 时间复杂度 0(N^2)
3. 空间复杂度 O(1)
4. 稳定的排序算法
2.1.2 希尔排序 O(N^1.3)
在学希尔排序之前,我们先对比一下同为 O(N^2) 量级的两个排序,插入和冒泡。
他俩的结构很像,都是将数据们分成:已经排好的区域,和还没排好的区域。但是在每轮排序过程的处理方案时出现了分歧,冒泡排序是一定会再次遍历一遍那块没排好的区域,然后将一个数据落入已经排好的区域,但是插入排序有可能不用完全遍历那块已经排好的区域,甚至只用访问一次那块区域 (tmp >= a[end]),就可以从没排好的区域中落一个数据进入已经排好的区域。换句话说插入排序有很强的适应性,它几乎每轮排序都不是最坏的情况,甚至都还不错,这是冒泡排序达不到的,冒泡排序只会把每轮排序都当作最坏的情况处理。
正是因为这个原因,在处理大量数据的绝大多数情况下,插入排序的速度要比冒泡排序块很多。或者说得益于插入排序的第一个特性,元素集合越接近有序,直接插入算法的时间效率越高,在绝大多数任务中插入排序的效果明显好于冒泡排序。
那么我们该如何放大这个优势,优化插入排序,让其排序速度更快。这时聪明的希尔就有了这样一个思路,将排序过程分成两步。第一步是预排序:将数据们都整理的越来越有序,第二步是执行一次插入排序,经过这两步操作数据集合就有序了。
那么有的同学这时候就开始怀疑了,这也没看出来什么神奇的思路,这个希尔排序怎么就好了,那么我展示一下用我们学过的四种排序处理 100,000 个随机数据的用时(ms),1,000,000个数据冒泡实在是跑不出来我们就看前3个,10,000,000个数据插入也跑不动了我们看剩下两个
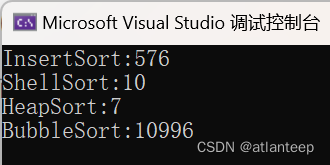
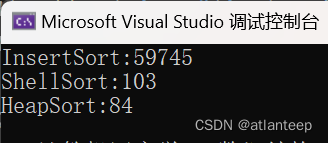
100,000个随机数据 1,000,000个随机数据
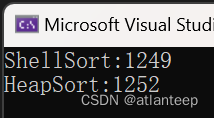
10,000,000个随机数据
看到了吗,希尔排序对于插入排序产生了巨大的优化,甚至在数据量巨大的情况下,其速度竟然超过了堆排序。
这个测试就是开了几块空间往里头填相同的随机值,让这几种排序方法分别给这几块空间进行排序,记录了各自排序的时长,这个测试时长的代码挺简单的,这里我就不写了,如果想要可以评论区说一下
2.1.2.1 预排序
预排序的思路就是选定一个整数n,把待排序集合中的所有数据分成n组,所有距离为n的数据分在同一组内,并对每一组内的数据进行排序。这样做的好处就是让大的数尽快到后面,小的数尽快到前面,选定的整数n越大,数字移动的越快,但是数据集合越不接近有序
这里我们选定整数为3,因此所有数据被分成了3组 (黑、红、蓝)

接下来就是给这三组数据分别排序,我们一步一步的展示如何写出一个排序
第一步,是写出一次排序的代码

这里我们就能发现其实这跟插入排序的一轮排序是一样的,只是将自增自减的地方改成了加gap减gap
第二步,将一组排序

到这里我们将黑色组完成了排序,其实就是加了一层循环让每次排序跑起来
第三步,将每组都排序
首先我们能想到的就是再套一层循环控制排完一组再去排下一组
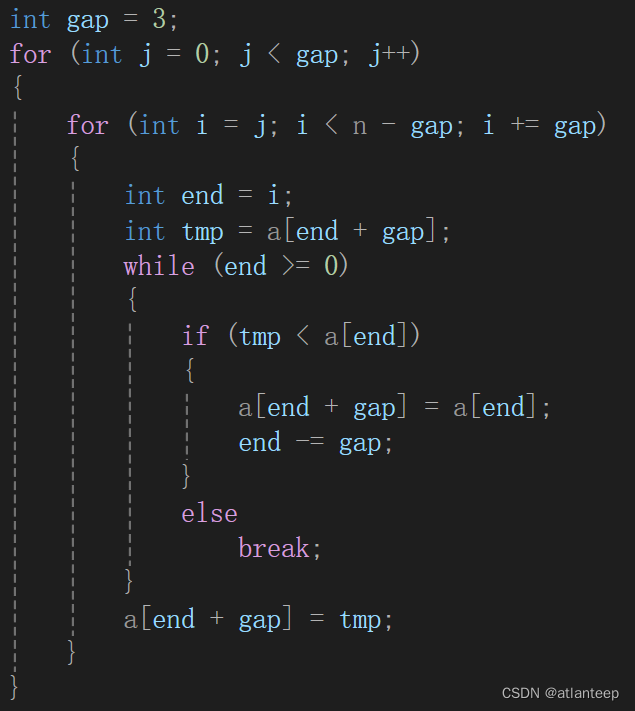
但是我们还可以这样操作:控制完这组的第一个再控制下一组的第一个,每组第一个控制完之后,控制每组的第二个,这样并不会有负面影响,就相当于将每组的排序拆开来进行,大家可以体会一下这个过程,这样就只用一层循环就能解决问题

但是他俩的效率是一样的,只是这种方法代码量小了一点,还有就是这种方法看起来相当的天才
到这里预排序就完成了,现在的数据集合已经变成了一个比较有顺序的集合了
2.1.2.2 控制gap完成排序
我们前面提到过gap越大,数据跳的越快,大的数据更快到后面,小的数据更快到前面,但是越不接近有序。gap越小数据跳的越慢,但是越接近有序,gup == 1时就是插入排序,数据集合直接就有序了。
所以说我们要靠控制合适的gap值来达到时间效率的提升,这时有人想到了用这样的方法
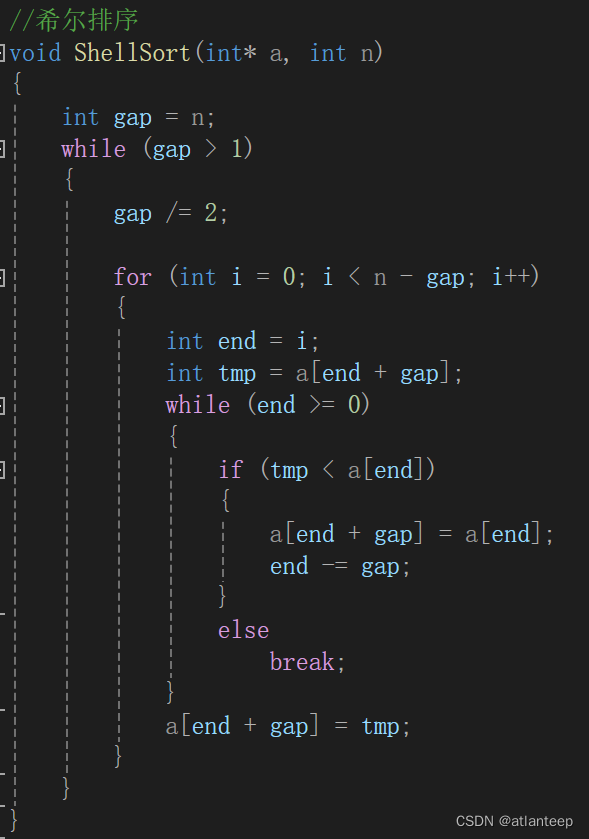
让gap每次除2,让数据元素处理的很有调理,还保证了最后一个值一定是1 ,因为一个大于1的数除2商一定为1。
后来还有人提 gap = gap / 3 + 1 的方案,总之到现在为止还没有哪一种主张得到了充分的证明。
对于希尔排序的时间复杂度计算到现在也还没有定论,有人利用大量的实验统计出当数据集合容量n很大时,时间复杂度大概在 O(N^1.25) 到 O(1.6*N^1.25) 之间,为了好记我就认为是 O(N^1.3)
最后,希尔排序是不稳定的排序算法
2.2 选择排序
基本思想:
每一次从待排序的元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到所有待排序的元素都处理完
2.2.1 直接选择排序 O(N^2)
这里我们每次找出最大和最小两个数据分别弄到数组尾部和头部,这样能节省一半的循环操作。因为我们每次排序都是交换两次数据,那就有可能刚交换完一次数据之后第二次又交换回去了,这样排序就出错了,这点要特别注意一下

直接选择排序是不稳定排序算法,因为可能把很前面的一个大数据换到很后面,打乱了原本的顺序
2.2.2 堆排序 O(N*logN)
堆排序我们刚讲完,这里就展示一下代码
数据结构·二叉树(一)-CSDN博客文章浏览阅读978次,点赞24次,收藏23次。本节介绍了二叉树的概念,基于完全二叉树引出了堆的概念,并着手实现了一个小根堆,最后我们介绍了堆应用中的堆排序和TOP-K问题,堆排序的时间复杂度是跟快排一个量级的,很有意思https://blog.csdn.net/atlanteep/article/details/136437696?spm=1001.2014.3001.5501


堆排序是不稳定排序算法
2.3 交换排序
基本思想:
根据元素集合中两个元素的大小比较结果来对换两个元素的位置,交换排序的特点是将较大的值向集合尾部移动,较小的值向集合首部移动
2.3.1 冒泡排序 O(N^2)
这个太简单了,直接上代码

冒泡排序是稳定的排序算法
2.3.2 快速排序 O(N*logN)
快速排序是霍尔于1962年提出的一中二叉树结构的交换排序方式,其基本思想为:任取待排序元素序列中的某元素值作为基准值,利用基准值将元素集合分割成左子集合、基准值、右子集合。小于基准值的元素都放到左子集合,大于基准值的元素都放到右子集合。然后左右子集合重复该过程,直到所有元素都到达自己相应的位置上。
下面我们解释一下,当元素右边都是小于它的值,左边都是大于它的值,那么我们是不是就可以认为这个元素已经到达了它相应的位置上。之后我们再将基准值的左右子集合中找到一个数放到它相应的位置上,不停的递归这一过程,最后元素集合不就有序了吗,这是快速排序的核心思想,大家可以理解一下。
这里我直接展示一次排序的代码,然后咱们根据这个代码讲解一下

这里我们搞一组数据,一般都是将第一个数据设成基准值,或者说关键值

然后我们让right指针先走,当找到小于基准值的数据时就停下来,然后再让left指针走,找到大于基准值的数据停下来,然后交换left指针和right指针指向的两个元素
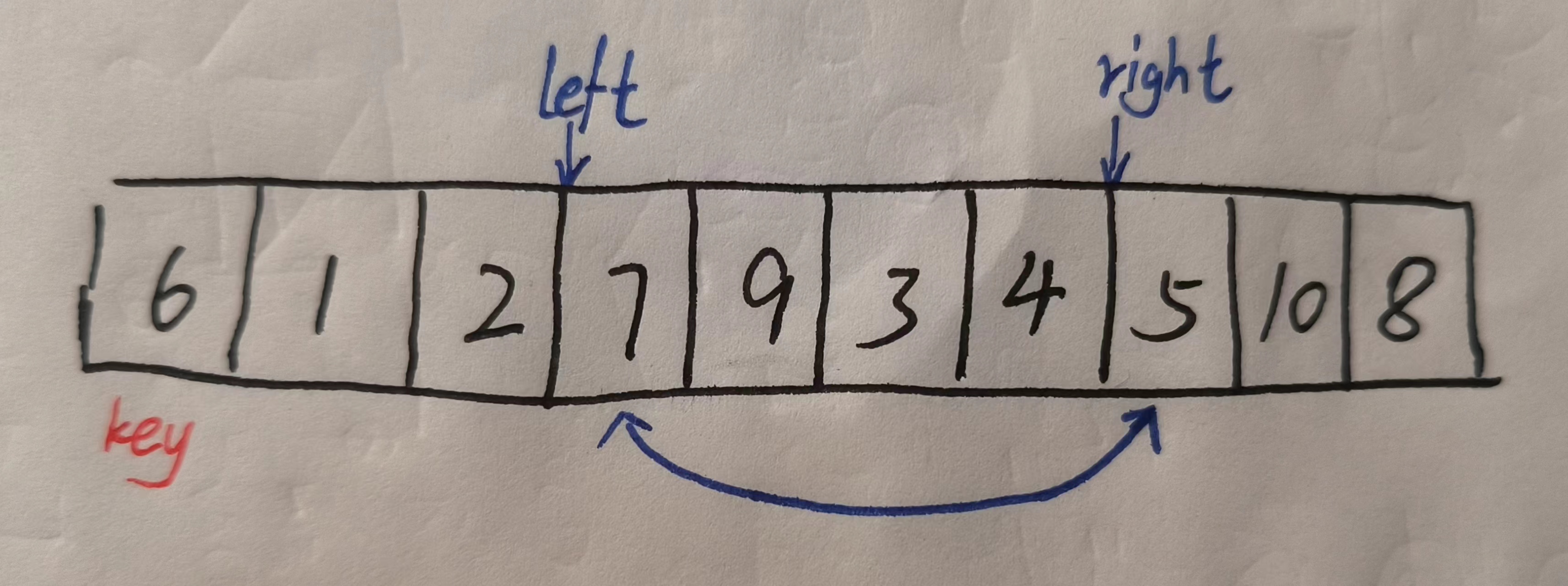
就这样一直让左右指针找下去,直到他俩相遇,此时把它们同时指向的元素和基准值交换,因为要交换基准值,所以我们记录基准值时并不是记录它的值,而是记录它所在的下标keyi,否则就根形参一样不会正确的交换。
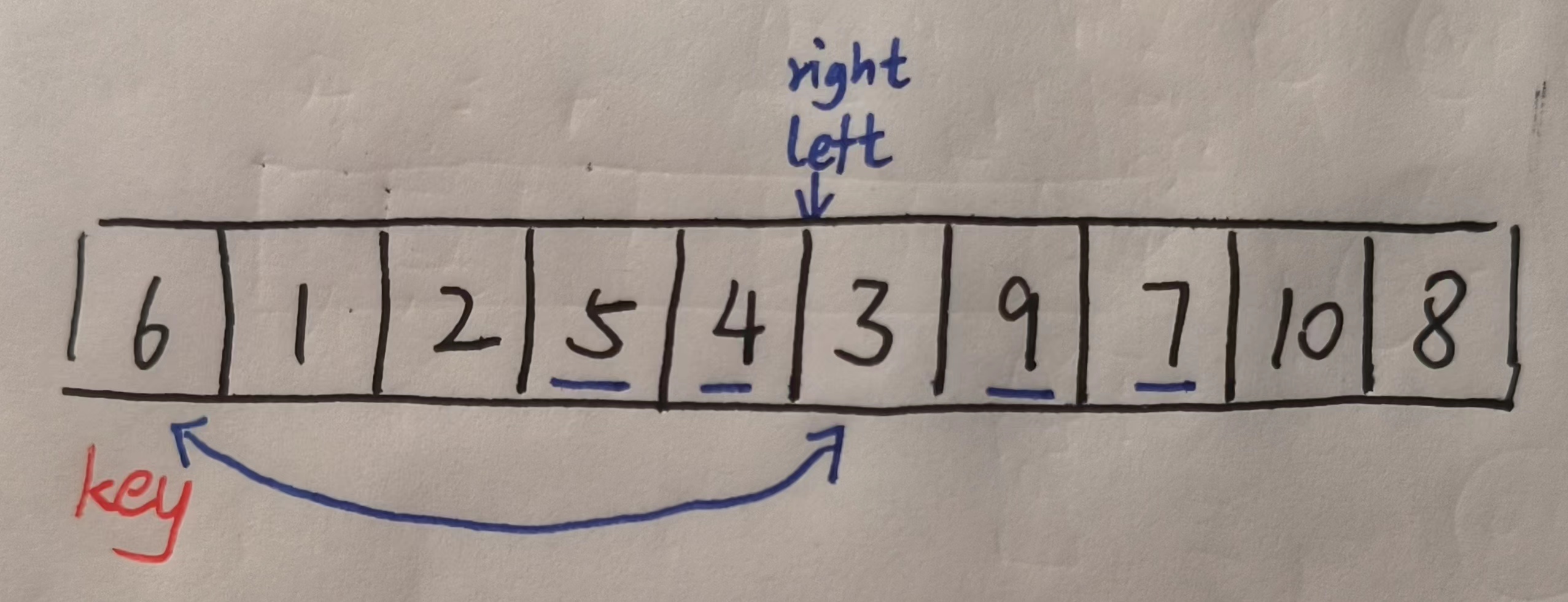
我知道,此时一定有同学会怀疑,为啥最后一步可以就这么直接交换呢,万一俩指针同时指向的值比key大怎么办。
其实,结论是俩指针同时指向的值是一定比key小,大家可以思考一下。
只要left和right之间有比key小的值,那么经过交换后,这个比key小的值一定会到left指针底下,此时如果left和right之间没有比key小的值了,那么下一次移动right就会停到left指针上面,此时他俩同时指向的值因为上一步的筛选一定比key小,这就是让right指针先走的特性。
那如果从一开始left和right之间就没有比key小的值,那么right指针就会直接走到left指针上,也就是key上,此时交换一俩指针同时指向的值和key就相当于没交换,还是正确的。
所以说经过这一次排序之后数组就变成了这样。

此时6到达了它相应的位置,之后的排序就是去递归处理6左边的区域和右边区域即可,注意左右区域是不包括key的
那么递归的最小子问题就是没有区域或者区域里只有一个值。
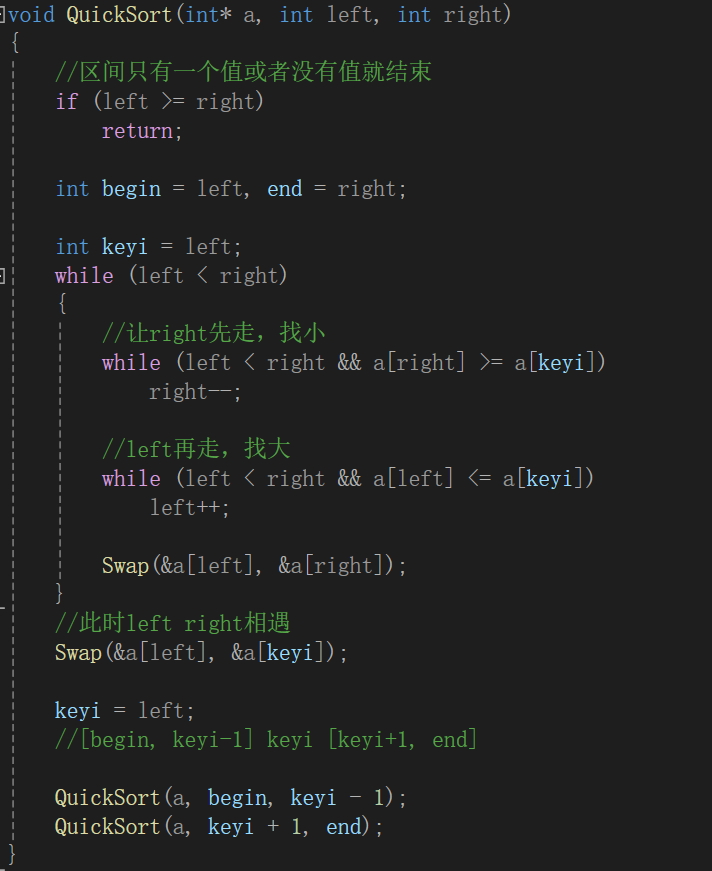
快排是不稳定的排序算法
2.3.2.1 快速排序优化
我们先跑一下快排,看看排1,000,000个数据和10,000,000个数据的用时
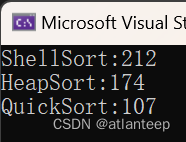
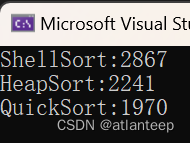
1,000,000个数据 10,000,000个数据
我们发现在数据完全随机的情况下,快排的效率还是很不错的,同样是二叉结构它比堆排块的原因是堆排的建堆是有些消耗的。
我们思考一下快速排序的时间复杂度到底是多少,因为它的思路于二叉树相同,所以说如果每次选出的key值都可以到区域最中间的情况是最好的,因为这种情况完全符合二叉结构,那么此时的时间复杂度就是 O(N*logN)。但是如果情况较坏,就是说数据集合是有序或者接近有序的情况下,时间复杂度就会来到 O(N^2)。
那么我们该如何优化这一缺陷,事实上我们可以在left和right控制的区间中随机选一个数,与left指向的数据交换位置,就像这样,我们成这种方案叫随机选key
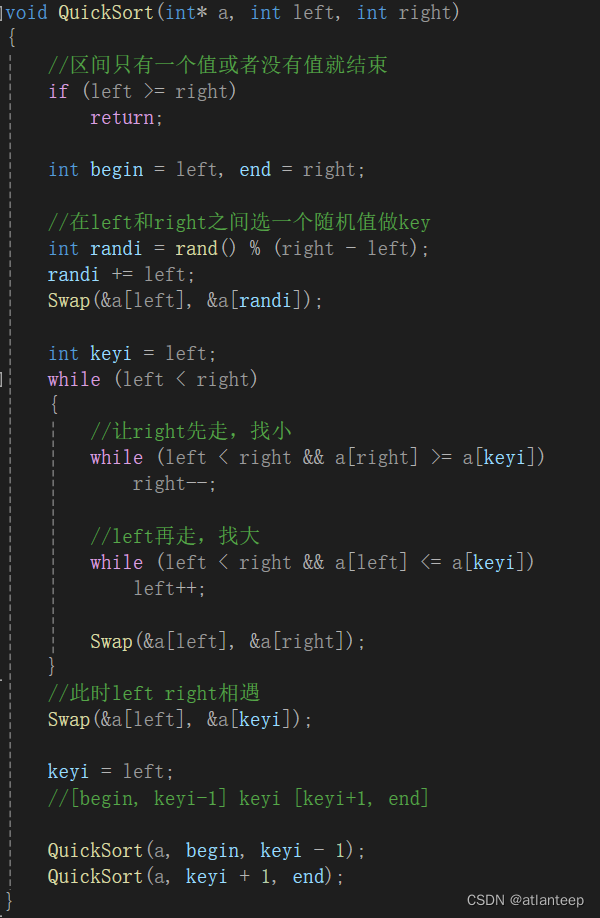
那么此时可能有人就认为这种随机的方法还是不靠谱,还是有几率出现最坏的情况,所以就又有人提出另一种解决方案叫三数取中
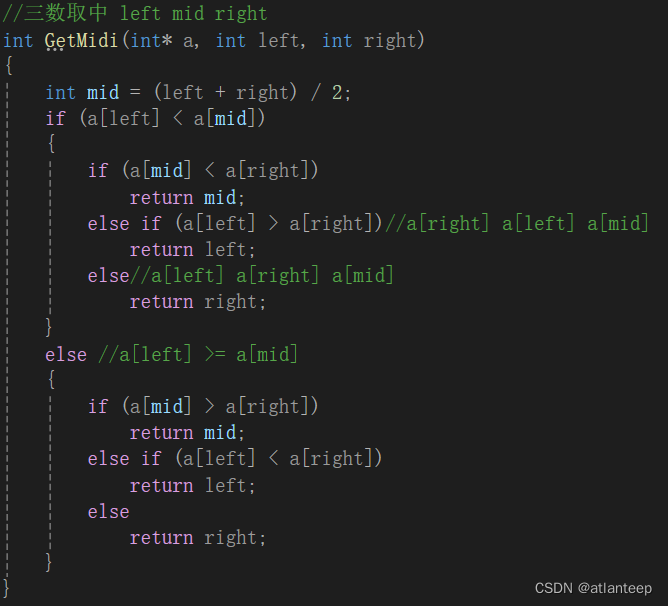
这段函数让我们从left到right区间取出了一个既不可能是这段区域中的最大值也不可能是最小值的数据的下标,下一步到了快排函数中让这个下标指向的数据与a[left]交换就行了,后面的代码的处理方案与随机选key是一样的
这个子函数的作用就是保证了取出来的值一定不是最大值也不是最小值,也就是说这样一来就一定不会出现最坏情况了,同时如果给出的任务集合是有序或接近有序的情况下,一下子就遍成了三数取中方案的最好情况
其实随机选key和三数取中两个方案,还是三数取中效率上好一点,但是随机选key的代码较短,最后还是根据实际情况自行取舍吧
最后还有一种叫小区间优化的方案,这个优化方案与随机选key和三数取中优化的地方是不一样的,并且这个方案的优化效果不明显。
我们知道二叉递归,如果是一个满二叉树的话,最后一层的递归次数占总次数的50%,倒数第二层的递归次数占总次数的25%,也就是说后三层递归节点占了整颗树的87.5%。因此有人提出也许我们不需要递归的那么深,就是说不用非得让区间中的数据只剩一个或者没有再返回,可以让区间中还剩10个值的时候,我们给这10个值插入排序就行了。为什么选择插入排序,因为数据量不大,不用使用堆排序或希尔排序,抛去他俩肯定就插入最好了。
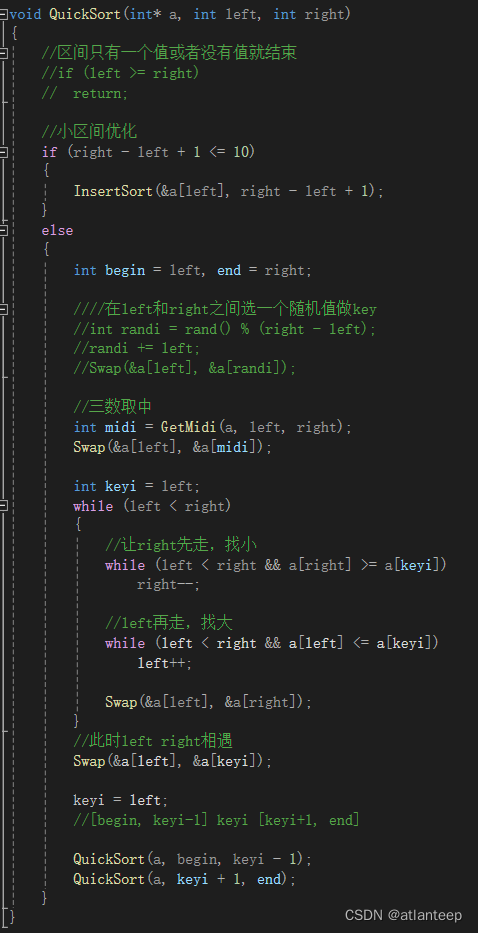
2.3.2.2 双指针快排法
这种双指针的方法是后人在希尔大佬的思想下延伸出来的另一种快排写法,这种写法的代码量被大大缩减了,同时时间效率相同
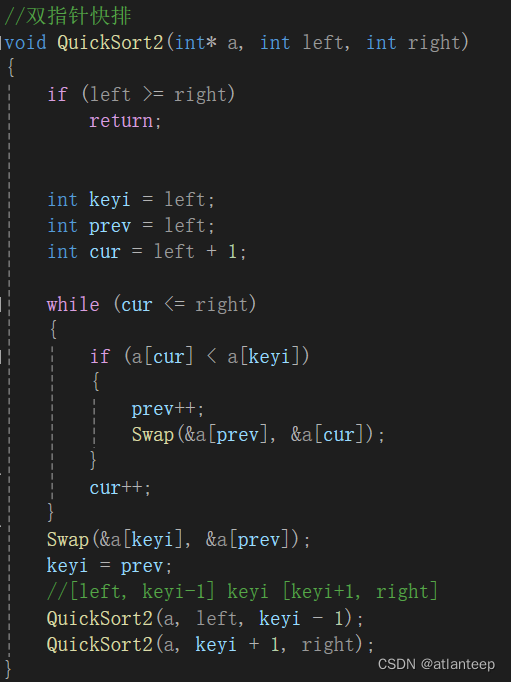
一样的,还是先选好一个关键值key,然后创建prev指针和cur指针

当cur指向的值大于等于key cur指针向后移动一位
当cur指向的值小于key prev指针向后移动一位,同时交换 prev 和 cur 指向的两个值,然后再将cur指针向后移动一位
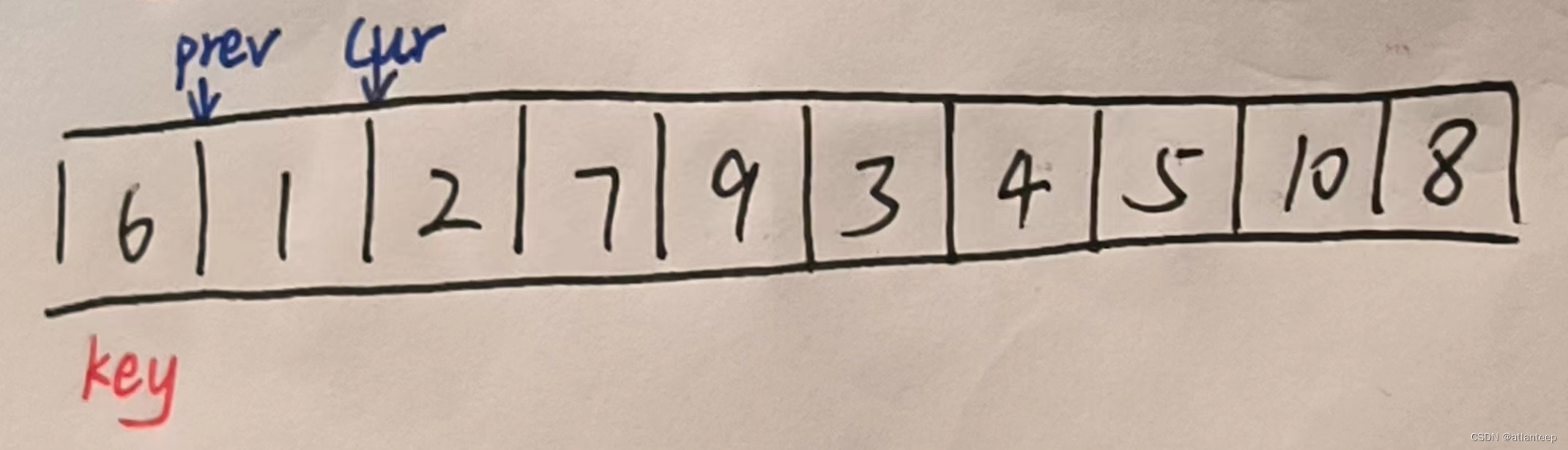

最后当cur遍历完整个数组之后就变成了这样,然后我们将key与prev指向的数据交换
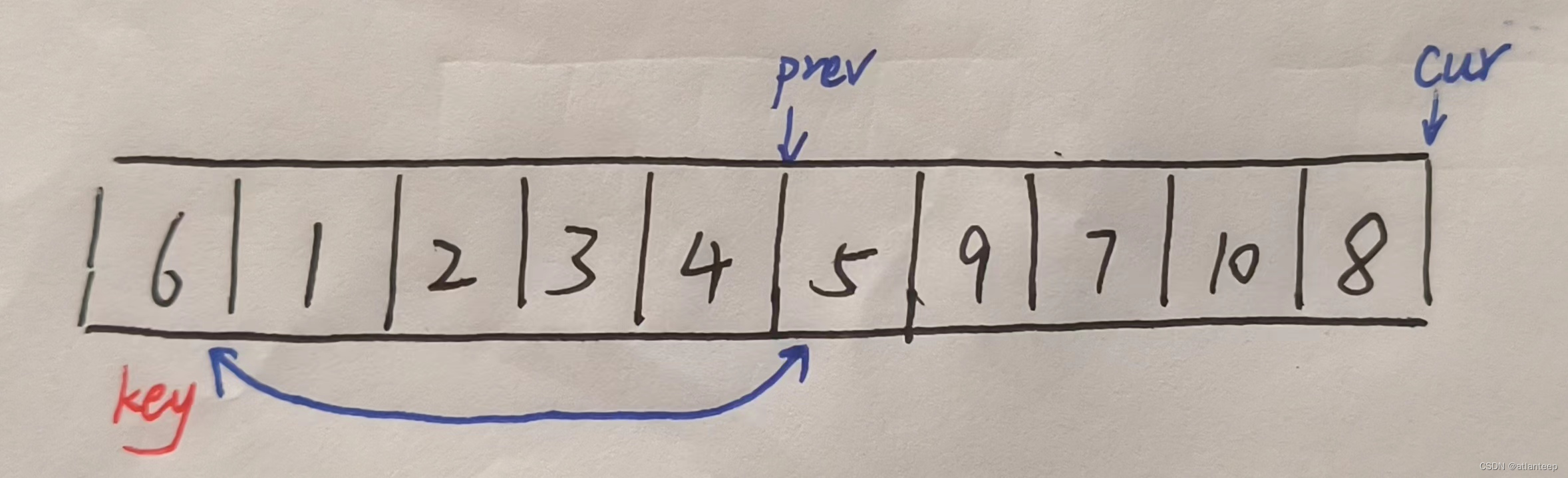
此时的效果就是key到达了它对应的位置了。
这个放方法的关键就是保证了prev指针前面的元素都小于key(key除外),最后当cur指针遍历完数组的时候数组中所有小于key的数据都会出现在prev指针之前(key除外),并且prev指向的元素一定小于key,或者压根就是key。大家可以多走读几遍,理解一下这里面的逻辑 。
我们直接上代码
2.3.2.3 非递归快排法
如何绕开递归来实现快排呢,我们需要借助到栈。首先将需要排序的左右区间压入栈中,处理完后将这对控制区间的数字出栈,此时又出现了两个区间,我们先将右区间压栈,再将左区间压栈。然后取栈顶元素,取到了左区间进行处理并出栈,此时又出现两个区间······如此操作下去,如果区间中只有一个或没有值就不入栈,最后栈为空就说明都处理完了,记得销毁栈。
这里我们用双指针的方式处理一次排序
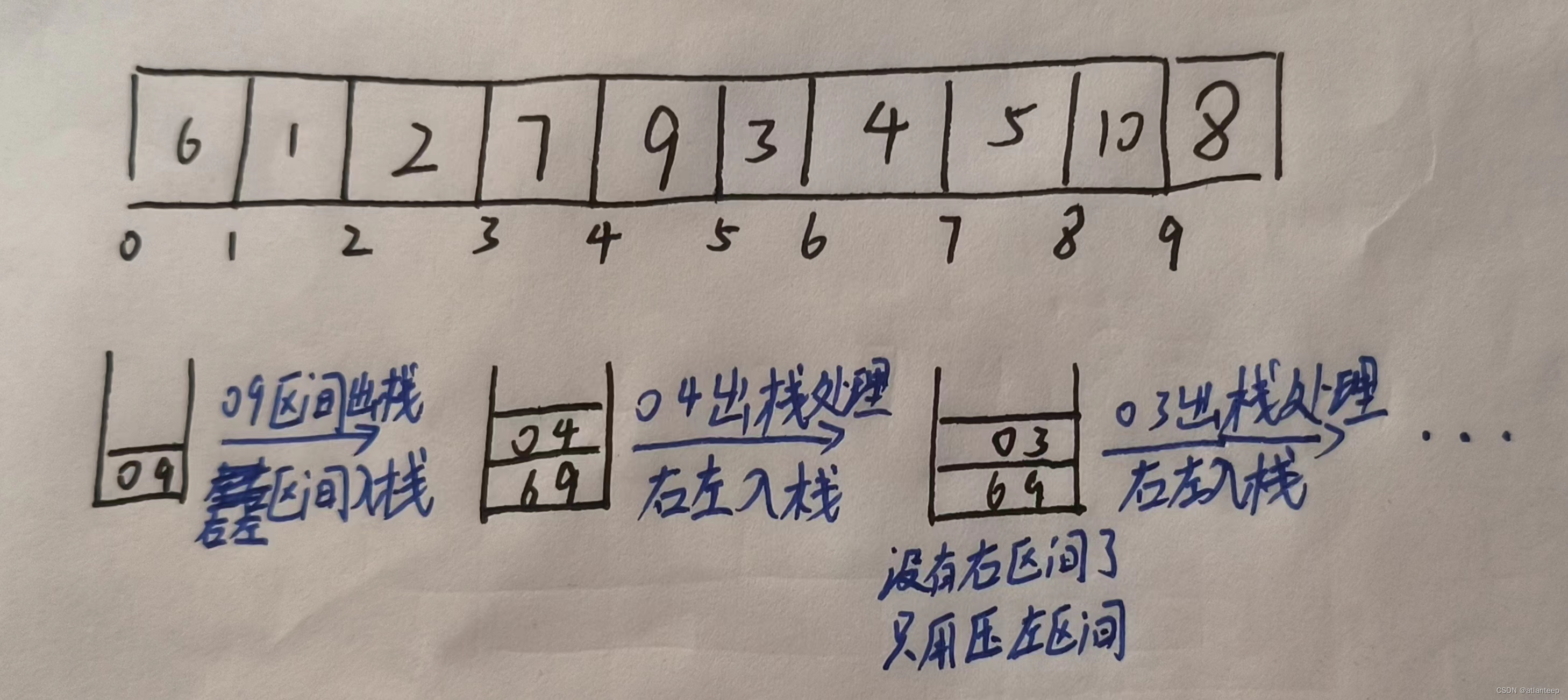
这里我给出的数据集合案例不太好,大家能明白是什么意思就行,其实这就是用栈后进先出的特点实现了类似递归的功能。
再实际敲代码的时候我们要不要把栈中元素的类型改成一个二元数组来表示区域呢?其实不必,我们只要保证:先压右边界再压左边界对应先取左边界再取右边界的顺序就好。进两个区域的时候也同理,一直保证先压右区域再压左区域,相当于后处理右区域,先处理左区域。
处理就是单趟排序,将key放到它对应的位置
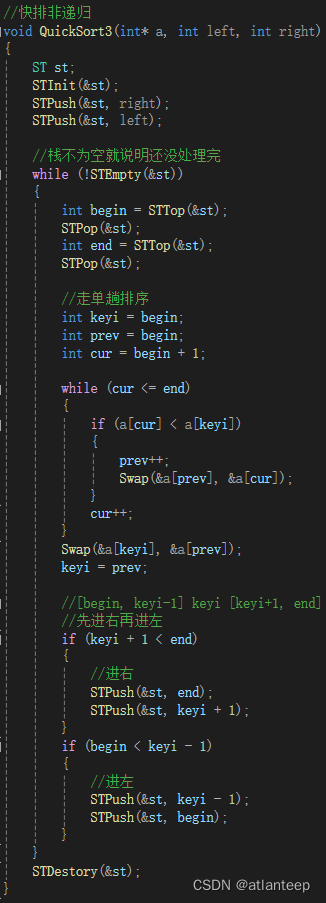
这个用栈模拟递归的思路还是很巧妙的,那我们为什么要有这种非递归的需求呢?是因为函数栈帧(函数调用所需空间)是建立在操作系统的栈(这个栈与我们自己写的栈是完全两回事)上的,这个操作系统的栈比较小,如果我们的递归深度太深就会导致栈溢出,从而崩掉。而我们自己写的栈是建立在堆区上的,这块区域相对来说就比较大了,不会出现类似栈溢出的问题。
事实上非递归还可以用队列实现,队列拥有先进先出的特点,那么在实现的时候我们就能看到队列是以层序遍历的结构在进行处理的,先处理左区域,然后把左区域中的左右区域入队列,pop掉左区域,然后取队头就是右区域,处理完之后同样把右区域中的左右队列入进来,pop掉右区域。此时一层就处理完了,然后接下来去处理下一层。只是这种处理结构与递归时的结构思路不同,我就不重点讲解了。
2.4 归并排序 O(N*logN)
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已经有序的子序列合并,得到完全有序的数列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。

单趟归并中,我们拿到两个有序的数组之后,用4个指针控制着向后走,哪个begin指针指示的数据小就入到新开辟的空间tmp中,直到有一个数组遍历完,再把另一个数组剩下的数据粘到新开辟的空间tmp中
归并排序我们还是要用分治的思想借助递归完成,当分开的区域中就剩一个数据的时候就可以开始返回了

归并排序的思路很简单,但是其中的一些控制细节需要用点心
归并排序是稳定的排序算法
2.4.1 非递归归并
如果像快排那样用栈实现的话,我们想一下就会发现不现实,因为快排单趟排完之后就不用那块区间了,或者说快排的排序发生在逻辑树展开的过程中,等逻辑树到达了所有叶节点(区间大小<=1)之后排序就结束了。但是归并的排序是发生在逻辑树回归的过程当中,将区域从1开始慢慢扩大,每扩大一次就实现一次单趟归并,我们都将上一块区域的界限pop掉了,找不到上一级的区域界限那就归不动了。
所以我们要换一种思路,将相邻数据区间进行归并,这样做的时间复杂度不变,但是思考方案确实与递归不同了
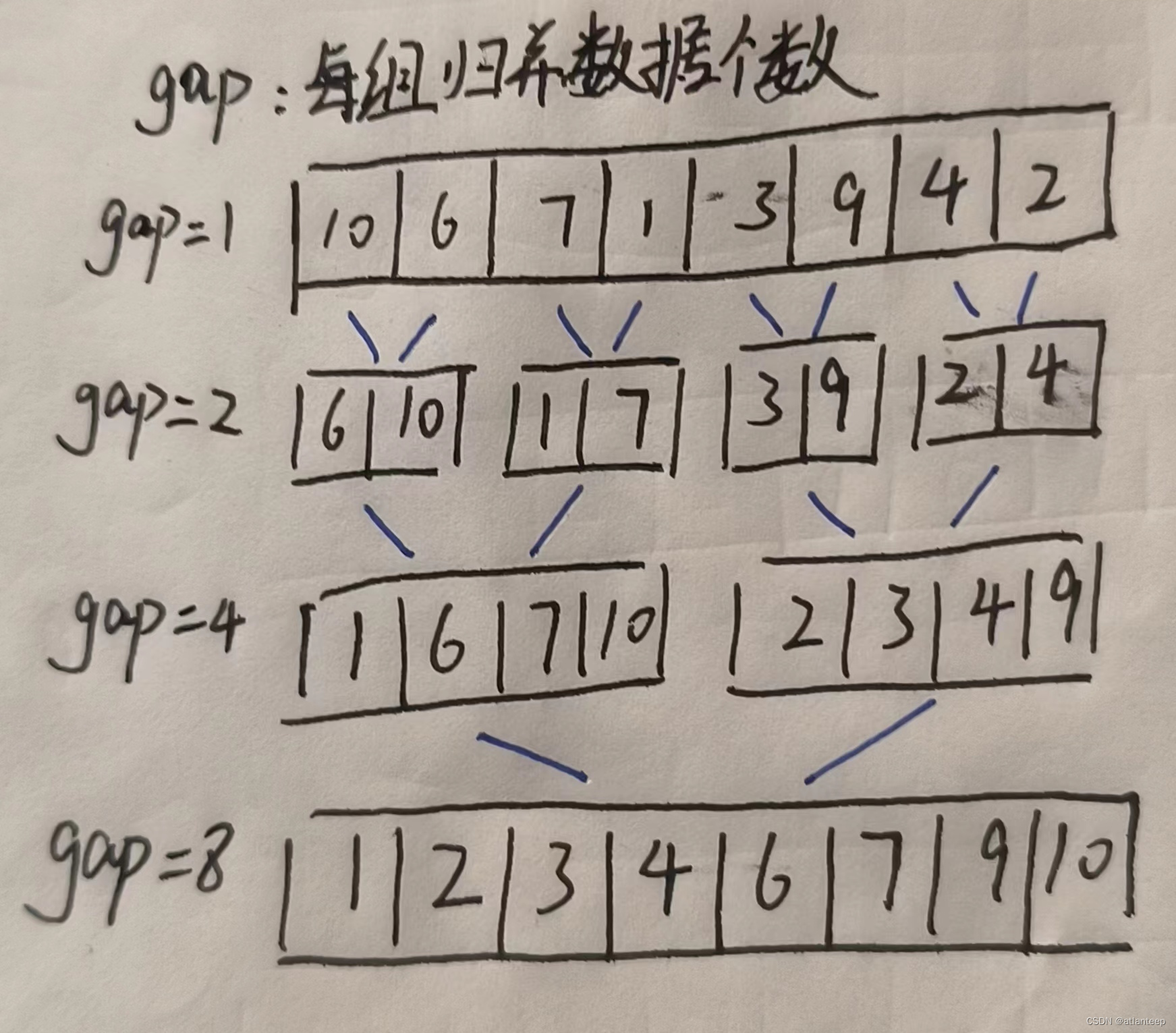
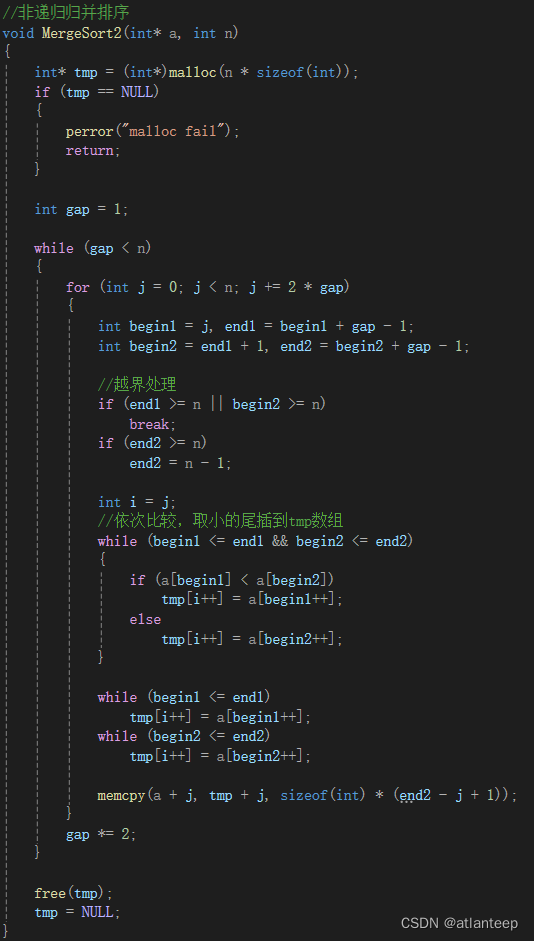
非递归的主要难点不是思路,而是越界处理的细节控制
2.5 非比较排序
前面我们讲到的排序都是比较排序,核心都是通过比较大小进行排序的。而非比较排序的核心不在比较,常见的非比较排序有:计数排序、基数排序、桶排序,非比较排序都是小众且局限的排序方案,这里我们仅讲解计数排序
2.5.1 计数排序 O(N)
计数排序的思路很简单,就是再弄一个计数数组,下标对应任务数组的值,然后扫描任务数组,比如任务数组出现了一个6,那就在计数数组下标为6的位置加1。如此做的意义就是任务数组中一个值出现了几次,都会被计数数组在相应的映射位置上统计下来。
这种方案听起来是不是特别简单,而且时间复杂度就是O(N),空间复杂度是O(N)。但是这个方案有两个局限性:第一是只适合排整形,而实际应用中很少有这种需求;第二是只适合任务数组的值较为集中的情况,否则计数数组要开很大。
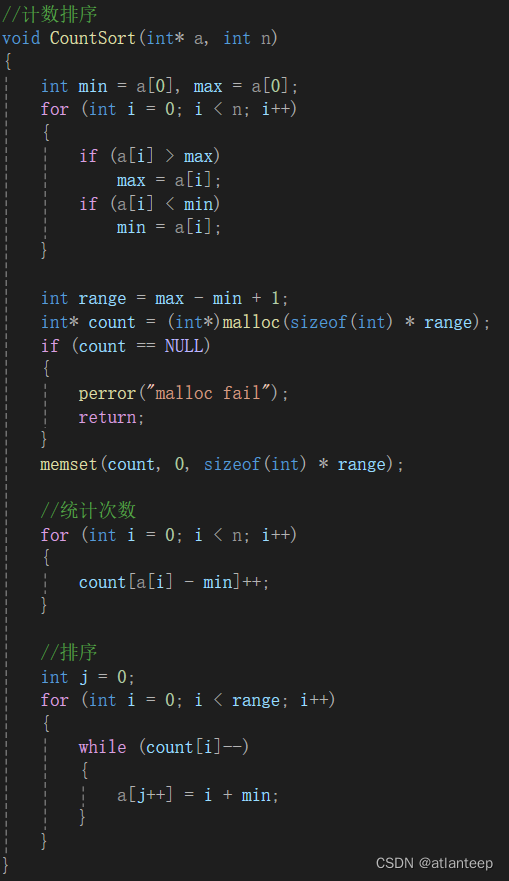
这里我还是简单说一下基数排序和桶排序吧,它们的原理是一样的,都是先排个位,再排十位,再排百位,这样往上排。区别就是基数排序直接用变量存储每次排序的结果,而桶排序是用链表存储的,比如个位是0的用链表串成一串挂起来,个位是1的用链表串成一串挂起来这样。这两种排序方案效率既低,消耗又大,同时还没有像冒泡排序那样的教学意义,总之就是很鸡肋。
3. 本节完整代码
Sort.h
#pragma once#include"Stack.h"
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<string.h>//时间计算
void TestOp();//打印数组
void PrintArry(int* a, int n);//交换
void Swap(int* p1, int* p2);//插入排序
void InsertSort(int* a, int n);//希尔排序
void ShellSort(int* a, int n);//直接选择排序
void SelectSort(int* a, int n);//堆排序
void HeapSort(int* a, int n);//快排
void QuickSort(int* a, int left, int right);//双指针快排
void QuickSort2(int* a, int left, int right);//快排非递归
void QuickSort3(int* a, int left, int right);//归并排序
void MergeSort(int* a, int n);//非递归归并排序
void MergeSort2(int* a, int n);//计数排序
void CountSort(int* a, int n);//冒泡
void BubbleSort(int* a, int n);
Sort.c
#include"sort.h"//打印数组
void PrintArry(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}//插入排序 O(N^2)
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){//变量end指示有序数列的最后一个位置int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}elsebreak;}a[end + 1] = tmp;}
}//希尔排序 O(N^1.3)
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap /= 2;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = tmp;}}
}//直接选择排序
void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){//选出最小值和最大值的位置int mini = begin, maxi = begin;for (size_t i = begin + 1; i <= end; i++){if (a[i] < a[mini])mini = i;if (a[i] > a[maxi])maxi = i;}Swap(&a[begin], &a[mini]);//防止maxi和begin重叠,从而交换两次的错误if (maxi == begin)maxi = mini;Swap(&a[end], &a[maxi]);begin++;end--;}
}//堆排序 O(N^logN)
void AdjustDown(int* a, int n, int parent)
{//假设法,选出大的孩子int child = parent * 2 + 1;//假设左孩子大while (child < n)//当child>=size时出数组了说明是叶子{if (child + 1 < n && a[child + 1] > a[child]){//找到小的那个孩子child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void HeapSort(int* a, int n)
{//数组直接建大堆for (int i = (n - 1 - 1) / 2; i >= 0; i--)AdjustDown(a, n, i);int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}//快速排序//三数取中 left mid right
int GetMidi(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right])return mid;else if (a[left] > a[right])//a[right] a[left] a[mid]return left;else//a[left] a[right] a[mid]return right;}else //a[left] >= a[mid]{if (a[mid] > a[right])return mid;else if (a[left] < a[right])return left;elsereturn right;}
}void QuickSort(int* a, int left, int right)
{//区间只有一个值或者没有值就结束if (left >= right)return;//小区间优化//if (right - left + 1 <= 10)//{// InsertSort(&a[left], right - left + 1);//}else{int begin = left, end = right;在left和right之间选一个随机值做key//int randi = rand() % (right - left);//randi += left;//Swap(&a[left], &a[randi]);//三数取中int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;while (left < right){//让right先走,找小while (left < right && a[right] >= a[keyi])right--;//left再走,找大while (left < right && a[left] <= a[keyi])left++;Swap(&a[left], &a[right]);}//此时left right相遇Swap(&a[left], &a[keyi]);keyi = left;//[begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}//双指针快排
void QuickSort2(int* a, int left, int right)
{if (left >= right)return;int keyi = left;int prev = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[keyi]){prev++;Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[keyi], &a[prev]);keyi = prev;//[left, keyi-1] keyi [keyi+1, right]QuickSort2(a, left, keyi - 1);QuickSort2(a, keyi + 1, right);
}//快排非递归
void QuickSort3(int* a, int left, int right)
{ST st;STInit(&st);STPush(&st, right);STPush(&st, left);//栈不为空就说明还没处理完while (!STEmpty(&st)){int begin = STTop(&st);STPop(&st);int end = STTop(&st);STPop(&st);//走单趟排序int keyi = begin;int prev = begin;int cur = begin + 1;while (cur <= end){if (a[cur] < a[keyi]){prev++;Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[keyi], &a[prev]);keyi = prev;//[begin, keyi-1] keyi [keyi+1, end]//先进右再进左if (keyi + 1 < end){//进右STPush(&st, end);STPush(&st, keyi + 1);}if (begin < keyi - 1){//进左STPush(&st, keyi - 1);STPush(&st, begin);}}STDestory(&st);
}//归并排序
void _MergeSort(int* a, int begin, int end, int* tmp)
{//当区间中只剩一个值的时候就返回if (begin == end)return;int mid = (begin + end) / 2;//[begin,mid] [mid+1,end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);//归并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;//依次比较,取小的尾插到tmp数组while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2])tmp[i++] = a[begin1++];elsetmp[i++] = a[begin2++];}while (begin1 <= end1)tmp[i++] = a[begin1++];while (begin2 <= end2)tmp[i++] = a[begin2++];memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(n * sizeof(int));if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp);tmp = NULL;
}//非递归归并排序
void MergeSort2(int* a, int n)
{int* tmp = (int*)malloc(n * sizeof(int));if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){for (int j = 0; j < n; j += 2 * gap){int begin1 = j, end1 = begin1 + gap - 1;int begin2 = end1 + 1, end2 = begin2 + gap - 1;//越界处理if (end1 >= n || begin2 >= n)break;if (end2 >= n)end2 = n - 1;int i = j;//依次比较,取小的尾插到tmp数组while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])tmp[i++] = a[begin1++];elsetmp[i++] = a[begin2++];}while (begin1 <= end1)tmp[i++] = a[begin1++];while (begin2 <= end2)tmp[i++] = a[begin2++];memcpy(a + j, tmp + j, sizeof(int) * (end2 - j + 1));}gap *= 2;}free(tmp);tmp = NULL;
}//计数排序
void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (int i = 0; i < n; i++){if (a[i] > max)max = a[i];if (a[i] < min)min = a[i];}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc fail");return;}memset(count, 0, sizeof(int) * range);//统计次数for (int i = 0; i < n; i++){count[a[i] - min]++;}//排序int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}
}//冒泡 O(N^2)
void BubbleSort(int* a, int n)
{for (int j = 0; j < n - 1; j++){int flag = 0;for (int i = 1; i < n - j; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);flag = 1;}}//当一趟冒泡结束后发现没有进行数据交换//说明已经有序了if (flag == 0)break;}
}相关文章:

数据结构·排序
1. 排序的概念及运用 1.1 排序的概念 排序:排序是将一组“无序”的记录序列,按照某个或某些关键字的大小,递增或递减归零调整为“有序”的记录序列的操作 稳定性:假定在待排序的记录序列中,存在多个具有相同关键字的记…...

Python学习笔记01
第一章、你好Python 初识Python Python的起源 1989年,为了打发圣诞节假期,Gudiovan Rossum吉多范罗苏姆(龟叔)决心开发一个新的解释程序(Python雏形) 1991年,第一个Python解释器诞生 Python这个名字,来自龟叔所挚爱的电视剧M…...

Java学习笔记01
1.1 Java简介 Java的前身是Oak,詹姆斯高斯林是java之父。 1.2 Java体系 Java是一种与平台无关的语言,其源代码可以被编译成一种结构中立的中间文件(.class,字节码文件)于Java虚拟机上运行。 1.2.3 专有名词 JDK提…...

SOC子模块---RTC and watchdog
RTC RTC大致执行过程: 对SOC 中的锁相环或者外部晶振的时钟进行计数;产生时,分,秒的中断;送给中断控制器;中断控制器进行优先权选择后送给cpu;Cpu执行中断服务程序;在中断服务程序…...

【测试开发学习历程】MySQL增删改操作 + 备份与还原 + 索引、视图、存储过程
前言: SQL内容的连载,到这里就是最后一期啦! 如果有小伙伴要其他内容的话,我会追加内容的。(前提是我有学过,或者能学会) 接下来,我们就要开始python内容的学习了 ~ ~ 目录 1 …...
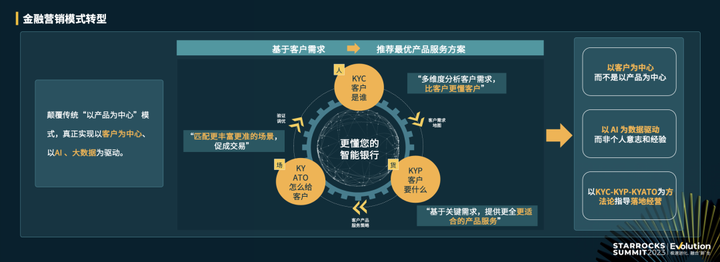
StarRocks 助力金融营销数字化进化之路
作者:平安银行 数据资产中心数据及 AI 平台团队负责人 廖晓格 平安银行五位一体,做零售金融的领先银行,五位一体是由开放银行、AI 银行、远程银行、线下银行、综合化银行协同构建的数据化、智能化的零售客户经营模式,这套模式以数…...
医院预约挂号系统设计与实现|jsp+ Mysql+Java+ Tomcat(可运行源码+数据库+设计文档)
本项目包含可运行源码数据库LW,文末可获取本项目的所有资料。 推荐阅读100套最新项目 最新ssmjava项目文档视频演示可运行源码分享 最新jspjava项目文档视频演示可运行源码分享 最新Spring Boot项目文档视频演示可运行源码分享 2024年56套包含java,…...

IIS7/iis8/iis10安装II6兼容模块 以windows2022为例
因安全狗的提示 安全狗防护引|擎安装失败 可能原因是: IIS7及以上版本末安装1IS6兼容模块! .所以操作解决 如下. 在开始菜单中,找到服务器管理器.找到下图的IIS,右键添加角色和功能,找到web服务器的管理工具选项,iis6管理兼容性 打钩并安装. 如下图...

Python爬虫-批量爬取星巴克全国门店
前言 本文是该专栏的第22篇,后面会持续分享python爬虫干货知识,记得关注。 本文笔者以星巴克为例,通过Python实现批量爬取目标城市的门店数据以及全国的门店数据。 具体的详细思路以及代码实现逻辑,跟着笔者直接往下看正文详细内容。(附带完整代码) 正文 地址:aHR0cHM…...

C/C++ 设置Socket的IP_TOS选项
IP TOS选项是指示IP报文转发的优先级,QOS控制的一种,常规的IP协议TOS都为0,就是普通报文。 设置: IPV4/TOS设置(Socket),IPTOS_LOWDELAY 表示FLASH优先级(一般用在游戏,…...

【tensorflow_gpu】安装合集
tensorflow_gpu与CUDA、cuDNN、Python版本对应关系 版本对应列表 tensorflow的清华源wheel tensorflow的清华源wheel列表 tensorflow_gpu安装指令 使用conda安装指定版本的tensorflow_gpu conda install tensorflow-gpu1.2.0使用wheel安装指定版本的tensorflow_gpu pip …...

Go 实现fsnotify
【官方操作】 package mainimport ("log""github.com/fsnotify/fsnotify" )func main() {watcher, err : fsnotify.NewWatcher()if err ! nil {log.Fatal(err)}defer watcher.Close()done : make(chan bool)go func() {for {select {case event, ok : <…...
Flink GateWay、HiveServer2 和 hive on spark
Flink SQL Gateway简介 从官网的资料可以知道Flink SQL Gateway是一个服务,这个服务支持多个客户端并发的从远程提交任务。Flink SQL Gateway使任务的提交、元数据的查询、在线数据分析变得更简单。 Flink SQL Gateway的架构如下图,它由插件化的Endpoi…...
)
阿里云国际设置黑白名单(针对高防实例IP)
DDoS高防支持针对高防实例设置黑名单和白名单,以拦截或放行指定IP的访问请求,配置后对该实例所有的业务生效。本文九河云介绍如何配置黑白名单。 功能介绍 黑名单IP的访问流量将被DDoS高防实例直接丢弃。白名单IP的访问流量将被DDoS高防实例直接放行。…...

Docker 入门使用说明
Docker 入门使用说明 Docker 安装 Docker 官网:Docker Docker 安装说明:Docker 安装说明 这里由于 Docker 在实时更新,所以每次安装 Docker 用来导入 key 的链接可能会有变化,这里就参考官方的安装方法即可 Docker 常用命令说…...
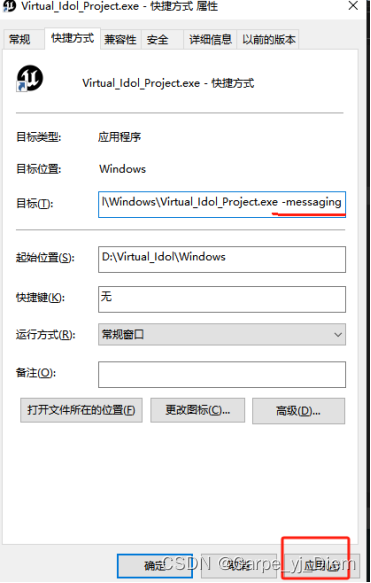
UE5 LiveLink 自动连接数据源,以及打包后不能收到udp消息的解决办法
为什么要自动连接数据源,因为方便打包后接收数据,这里我是写在了Game Instance,也可以写在其他地方,自行替换成Beginplay和Endplay 关于编辑器模式下能收到udp消息,打包后不能收到消息的问题有两点需要排查,启动打包后…...

国内ip切换是否合规?
在网络使用中,IP地址切换是一种常见的行为,可以用于实现隐私保护、访问地域限制内容等目的。然而,对于国内用户来说,IP地址切换是否合规一直是一个备受关注的话题。在中国,网络管理严格,一些IP切换行为可能…...

Flutter 3.13 之后如何监听 App 生命周期事件
在 Flutter 中,您可以监听多个生命周期事件来处理应用程序的不同状态,但今天我们将讨论 didChangeAppLifecycleState 事件。每当应用程序的生命周期状态发生变化时,就会触发此事件。可能的状态有 resumed 、 inactive 、 paused 、 detached …...

基于docker创建深度学习开发环境
基于docker创建深度学习开发环境 记录几个链接 第一步:配置docker环境,此处大把教程,不再赘述第二步:拉取nvidia做好的cuda和cudnn镜像: docker pull nvcr.io/nvidia/cuda:12.2.0-devel-ubuntu20.04如果有其他需求&a…...
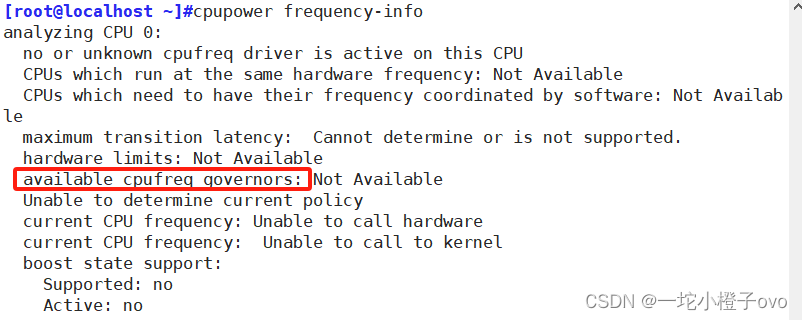
Linux系统——硬件命令
目录 一.网卡带宽 1.查看网卡速率——ethtool 网卡名 2.查看mac地址——ethtool -P 网卡名 二、内存相关 1.显示系统中内存使用情况——free -h 2.显示内存模块的详细信息——dmidecode -t memory 三、CPU相关 1.查看CPU架构信息——lscpu 2.性能模式 四、其他硬件命…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
