【数据结构】非线性结构——二叉树

文章目录
- 前言
- 1.树型结构
- 1.1树的概念
- 1.2树的特性
- 1.3树的一些性质
- 1.4树的一些表示形式
- 1.5树的应用
- 2.二叉树
- 2.1 概念
- 2.2 两种特殊的二叉树
- 2.3 二叉树的性质
- 2.4 二叉树的存储
- 2.5 二叉树的基本操作
前言
前面我们都是学的线性结构的数据结构,接下来我们就需要来学习非线性的数据结构,我们先来学第一个非线性的数据结构——树。每一门学科都来自生活,从生活中学习,我们要学的树就是来自生活,这种数据结构就像我们大自然中的树倒立着一样,所以我们取名为树。
1.树型结构
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
1.有一个特殊的结点,称为根结点,根结点没有前驱结点
2.除根结点外,其余结点被分成M(M > 0)个互不相交的集合T1、T2、…、Tm,其中每一个集合Ti (1 <= i <= m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
3.树是递归定义的。
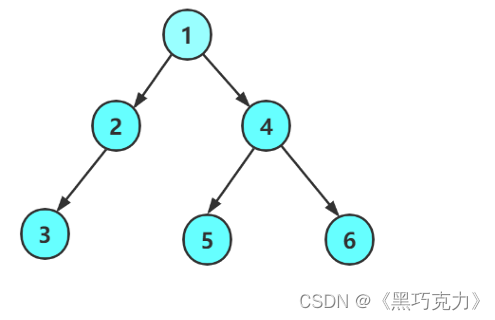
注意:树形结构中,子树不能有交集,否则不具备树形结构。
1.2树的特性
1.子树是不相交的
2.除了根结点以外,每一个结点只有一个父节点。
3.一棵N个结点的树有N-1条边。
1.3树的一些性质
**结点的度:**一个结点含有子树的个数称为该结点的度;
**树的度:**一棵树中,所有结点度的最大值称为树的度;
叶子结点或终端结点:度为0的结点称为叶结点;
**双亲结点或父结点:**若一个结点含有子结点,则这个结点称为其子结点的父结点;
**孩子结点或子结点:**一个结点含有的子树的根结点称为该结点的子结点;
**根结点:**一棵树中,没有双亲结点的结点;
**结点的层次:**从根开始定义起,根为第1层,根的子结点为第2层,以此类推
**树的高度或深度:**树中结点的最大层次;
**非终端结点或分支结点:**度不为0的结点;
**兄弟结点:**具有相同父结点的结点互称为兄弟结点;
**堂兄弟结点:**双亲在同一层的结点互为堂兄弟;
**结点的祖先:**从根到该结点所经分支上的所有结点;
**子孙:**以某结点为根的子树中任一结点都称为该结点的子孙。
**森林:**由m(m>=0)棵互不相交的树组成的集合称为森林
1.4树的一些表示形式
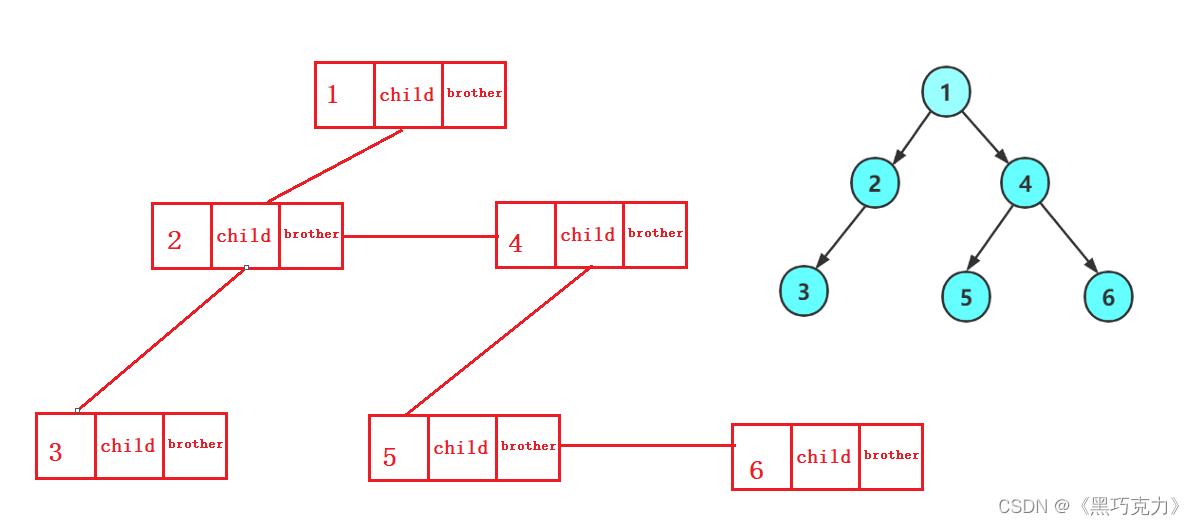
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,如:双亲表示法,孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
class Node {int value;
Node firstChild;
// 树中存储的数据
// 第一个孩子引用
Node nextBrother; // 下一个兄弟引用
}
1.5树的应用
文件系统管理(目录和文件)

2.二叉树
2.1 概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
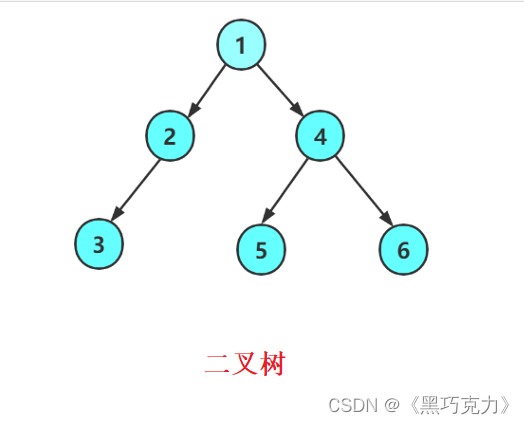
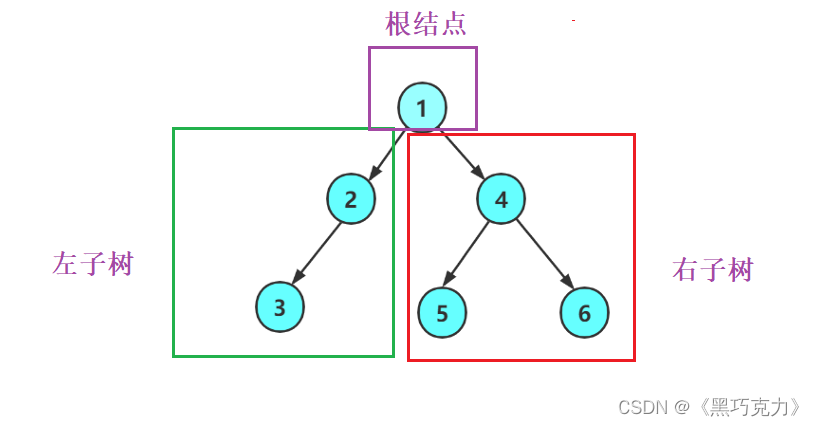
从上图可以看出: - 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
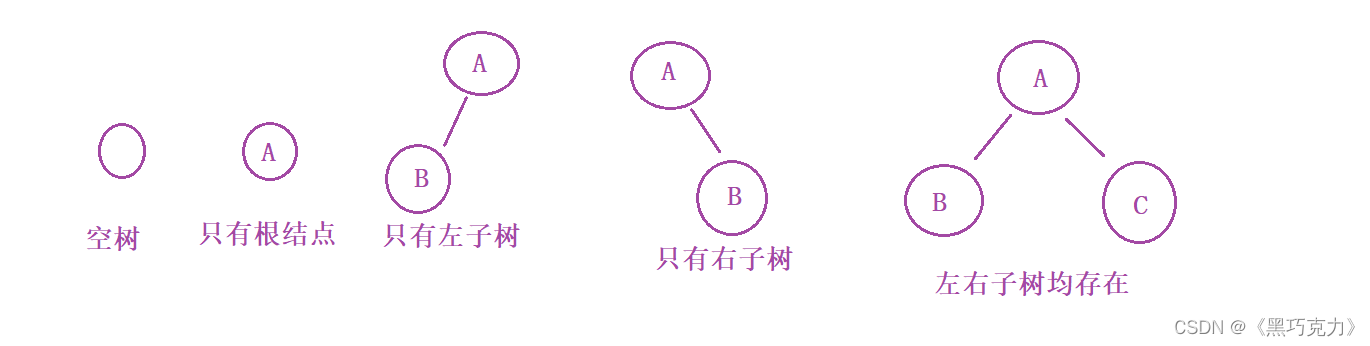
2.2 两种特殊的二叉树
- 满二叉树: 一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵二叉树的层数为K,且结点总数是,则它就是满二叉树。
- 完全二叉树: 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
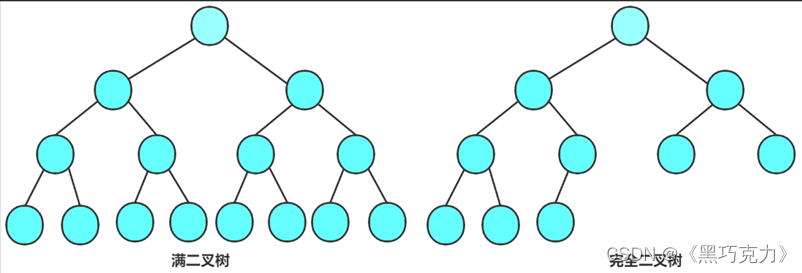
2.3 二叉树的性质
- 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有(i>0)个结点
- 若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是(k>=0)
- 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1
- 具有n个结点的完全二叉树的深度k为上取整
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i
的结点有:
若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
若2i+1<n,左孩子序号:2i+1,否则无左孩子
若2i+2<n,右孩子序号:2i+2,否则无右孩子
2.4 二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式,具体如下:
// 孩子表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}// 孩子双亲表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent; // 当前节点的根节点
}
这里我们用孩子表示法来构建二叉树。
2.5 二叉树的基本操作
2.5.1枚举法来将树创建,这种创建方式一开始是比较容易理解的,等到我们对二叉树学习到一定的程度再去用其他方法创建二叉树,那样就比较轻松。
枚举法创建树:
public class BinaryTree {static class TreeNode {public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val = val;}}public TreeNode careTree1() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');A.left = B;A.right = D;B.left = C;D.left = E;D.right = F;return A;}
}
2.5.2 二叉树的遍历
- 前中后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如:打印节点内容、节点内容加1)。 遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础。
在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱,如果按照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的。如果N代表根节点,L代表根节点的左子树,R代表根节点的右子树,则根据遍历根节点的先后次序有以下遍历方式:
NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点—>根的左子树—>根的右子树。
LNR:中序遍历(Inorder Traversal)——根的左子树—>根节点—>根的右子树。
LRN:后序遍历(Postorder Traversal)——根的左子树—>根的右子树—>根节点。
下面分析前序递归遍历图解与遍历结果
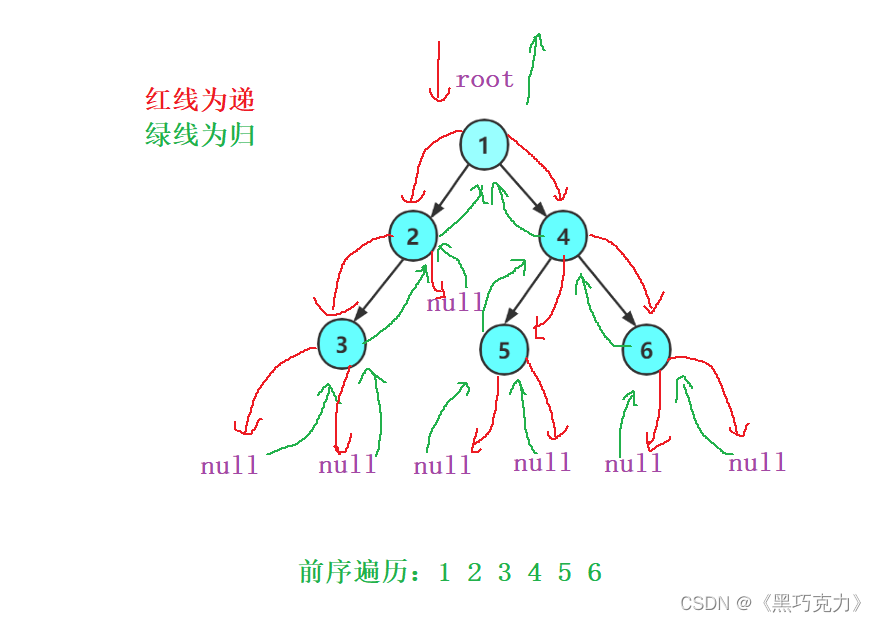
代码实现:
public void preOrder(TreeNode root) {if(root == null) {return;}System.out.print(root.val+" ");preOrder(root.left);preOrder(root.right);}
下面分析中序递归遍历图解与遍历结果
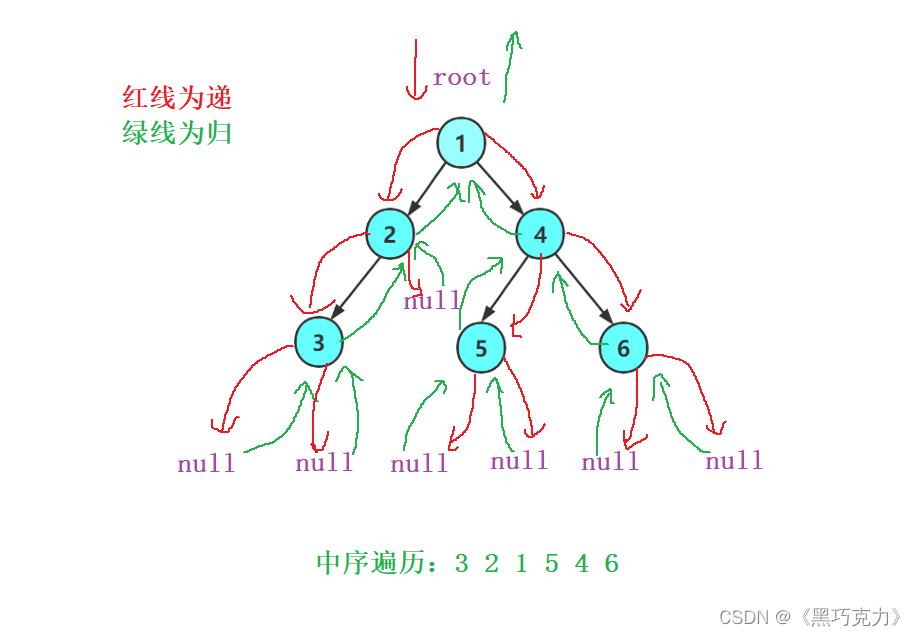
代码实现:
public void inOrder(TreeNode root) {if(root == null) {return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}
下面分析后序递归遍历图解与遍历结果
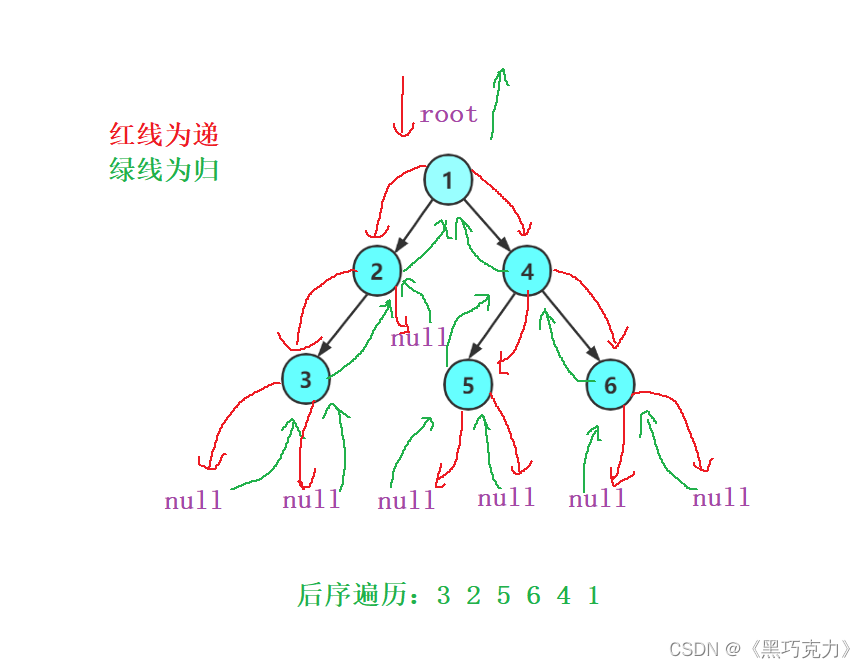
代码实现:
public void postOrder(TreeNode root) {if(root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val+" ");}
- 层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
2.5.3 二叉树的基本操作
这些操作我们都采用子问题方式来解决
什么叫子问题?子问题就是将问题细分成一个一个相同的小问题来解决。
1.获取树中节点的个数
左树的结点+右树的结点+根结点
int size(TreeNode root) {//子问题:左树结点的个数+右树结点的个数+根的个树if(root == null) {return 0;}return size(root.left) + size(root.right) + 1;}
2.获取叶子节点的个数
左树的叶子节点+右树的叶子节点 (叶子节点就是左右都没有结点称为叶子节点)
int getLeafNodeCount(TreeNode root) {if(root == null) {return 0;}//判断是否为叶子结点if(root.left == null && root.right == null) {return 1;}return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);}
3.获取第K层节点的个数
每一次遍历左子树或右子树的时候k-1,当k==1时直接返回1.
int getKLevelNodeCount(TreeNode root,int k) {if(root == null) {return 0;}//k==1时返回1if(k == 1) {return 1;}//遍历左子树和右子树return getKLevelNodeCount(root.left,k-1) + getKLevelNodeCount(root.right,k-1);}4.获取二叉树的高度
比较左子树和右子树的最大路径然后+1
int getHeight(TreeNode root) {if(root == null) {return 0;}//比较左子树与右子树的最大值然后加1int getLeftMax = getHeight(root.left);int getRightMax = getHeight(root.right);return Math.max(getLeftMax,getRightMax) + 1;}int getHeight1(TreeNode root) {if(root == null) {return 0;}//比较左子树与右子树的最大值然后加1return Math.max(getHeight1(root.left),getHeight1(root.right)) + 1;}
5.检测值为value的元素是否存在
先判断根结点,然后遍历左子树和右子树
TreeNode find(TreeNode root, int val) {if(root == null) {return null;}//判断根结点是否为检测值if(root.val == val) {return root;}//然后遍历左子树,判断有没有和val值相同的,有则返回,没有则遍历右子树TreeNode leftVal = find(root.left,val);if(leftVal != null) {return leftVal;}//然后遍历右子树,判断有没有和val值相同的,有则返回TreeNode rightVal = find(root.right,val);if(rightVal != null) {return rightVal;}//说明左子树找不到右子树也找不到,最后返回nullreturn null;}
希望大家可以给我点点关注,点点赞,并且在评论区发表你们的想法和意见,我会认真看每一条评论,你们的支持就是我的最大鼓励。🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹
相关文章:

【数据结构】非线性结构——二叉树
文章目录 前言1.树型结构1.1树的概念1.2树的特性1.3树的一些性质1.4树的一些表示形式1.5树的应用2.二叉树 2.1 概念2.2 两种特殊的二叉树2.3 二叉树的性质2.4 二叉树的存储2.5 二叉树的基本操作 前言 前面我们都是学的线性结构的数据结构,接下来我们就需要来学习非…...
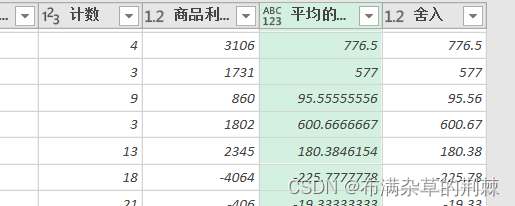
数据分析POWER BI之power query
1.导入数据 ctrla全选--数据--获取数据--其他来源--来自表格/区域 导入数据,进入编辑模式 2.整理与清除 清除:删除所选列的非打印字符 转换--格式--清除 修整:删除前面和后面的空格 转换---格式---修整(修整后前面后面的空格没有了…...

【c语言】详解操作符(上)
1. 操作符的分类 2. 原码、反码、补码 整数的2进制表示方法有三种,即原码、反码、补码 有符号整数的三种表示方法均有符号位和数值位两部分,2进制序列中,最高位的1位是被当做符号位其余都是数值位。 符号位都是用0表示“正”,用…...

VR全景展示:传统制造业如何保持竞争优势?
在结束不久的两会上,数字化经济和创新技术再度成为了热门话题。我国制造产业链完备,但是目前依旧面临着市场需求不足、成本传导压力加大等因素影响,那么传统制造业该如何保持竞争优势呢? 在制造行业中,VR全景展示的应用…...
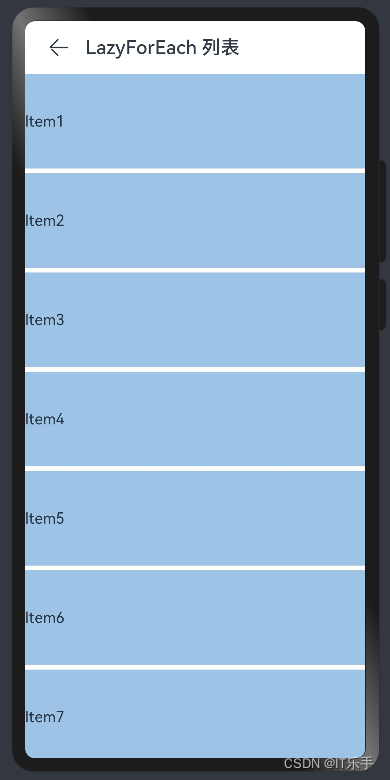
2.7、创建列表(List)
概述 列表是一种复杂的容器,当列表项达到一定数量,内容超过屏幕大小时,可以自动提供滚动功能。它适合用于呈现同类数据类型或数据类型集,例如图片和文本。在列表中显示数据集合是许多应用程序中的常见要求(如通讯录、…...

solr functionquery函数查询自定义函数实现
Solr是一个开源的搜索平台,基于Apache Lucene库构建,主要用于提供全文搜索的功能。它被设计为一个高度可靠、可扩展的搜索应用服务器。以下是Solr的一些主要使用场景: 全文搜索:Solr最核心的功能是提供全文搜索,它可以…...
如何将 Parallels虚拟机 安装或者迁移到 移动硬盘 or U盘?
本文讨论主题 如何安装 Parallels 虚拟机到移动硬盘和U盘? 已经安装到了mac上的虚拟机如何迁移到移动硬盘活着U盘上? 关于Parallels Deskshop 19 虚拟机 安装激活,文末关注公众号AIshape,回复:PD 进行获取通过将虚拟机安装在外置的移动硬盘U盘上,可以节省mac本身SSD的容…...

大型网站集群管理负载均衡
课程介绍 结合企业大规模应用,解决应用高并发问题,解决单节点故障问题,缓存数据库的应用。学完掌握知识点:企业应用实现四七层负载均衡,以及Nginx等应用的高可用性,Redis缓存数据库的部署应用以及高可用方…...

JAVA使用POI实现Excel单元格合并-02
JAVA使用POI实现Excel单元格合并 实现效果 解释:只要是遇见与前一行相同的数据就合并 引入jar <dependency><groupId>org.apache.poi</groupId><artifactId>poi-ooxml</artifactId><version>5.2.2</version></depe…...

深入了解 Linux 中的 MTD 设备:/dev/mtd* 与 /dev/mtdblock*
目录 前言一、什么是MTD子系统?二、 /dev/mtd* 设备文件用途注意事项 三、/dev/mtdblock* 设备文件用途注意事项 三、这两种设备文件的关系四、关norflash的一些小知识 前言 在嵌入式Linux系统的世界里,非易失性存储技术扮演着至关重要的角色。MTD&#…...

2、Spring CLI安装
安装 Spring CLI 提供了多种格式,让您选择自己喜欢的安装方法。可下载的制品可从发布页面获取。 二进制发行版 WindowsLinuxMac手动安装(Windows,其他自己看) spring-cli-standalone-<version>-windows.x86_64.zip - 打包了 x86 JDKspring-cli-installer-<versi…...
数据库备份工具(实现数据定时覆盖)
数据库备份工具(实现数据定时覆盖) 永远热爱,永远执着! 工具介绍 自动化测试数据库更新调度程序 这段 Python 脚本自动化了每天定时从生产数据库更新测试数据库的过程。它利用了 schedule 库来安排并执行每天指定时间的更新任务…...

测试环境搭建整套大数据系统(十二:挂载磁盘到hadoop环境)
一:链接硬盘 将硬盘连接到计算机的 SATA 接口或 USB 接口,并确保硬盘通电并处于可用状态。 二:查看硬盘信息 sudo fdisk -l三:创建分区 gdisk /dev/vbd重新扫描磁盘 partprobe /dev/vdb格式化磁盘 mkfs.ext4 /dev/vdb2查看磁…...

Spring事务核心:声明式事务注解式事务
全解:声明式事务和注解事务 在Spring中,事务管理是一个非常重要的特性,它可以帮助开发者在应用程序中实现事务控制。Spring提供了两种事务管理方式:声明式事务和注解事务。 1. 声明式事务 声明式事务是指通过配置文件或注解的方…...

AcWing 1015. 摘花生
Problem: AcWing 1015. 摘花生 文章目录 思路解题方法复杂度Code 思路 这是一个典型的动态规划问题。我们需要在一个二维网格中,从左上角走到右下角,每次只能向右或向下移动,目标是使得经过的路径上的数字之和最大。 我们可以定义dp[i][j]为从…...

Dalle-3、Sora、Stable Diffusion 3 掀起AIGC新浪潮
随着科技的飞速发展,我们迎来了视觉AIGC高光时刻,一个充满无限可能与机遇的新时代。在这个时代里,三大里程碑Dalle-3、Sora和Stable Diffusion 3以其炸裂式的技术发展,引领着AIGC领域的新浪潮。文章首先做相应简要介绍,…...
Unity 视频组件 VideoPlayer
组件添加: 在自己定义的组件下(例如:Panel) 点击 Inspector 面板中的 AddComponent ,输入“VideoPlayer”。 资源 这里 视频资源有两种形式,第一种是 VideoClip ,需要将视频文件拖拽到该属性字段…...
RSTP环路避免实验(华为)
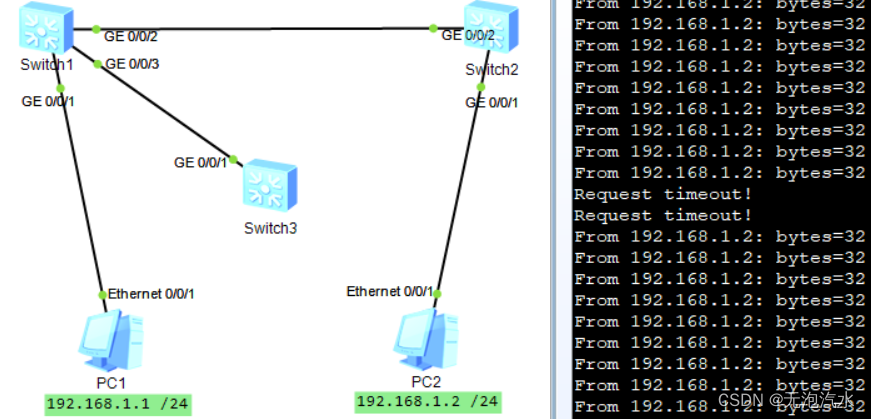
思科设备参考:RSTP环路避免实验(思科) 一,技术简介 RSTP (Rapid Spanning Tree Protocol) 是从STP发展而来 • RSTP标准版本为IEEE802.1w • RSTP具备STP的所有功能,可以兼容STP运行 • RSTP和STP有所不同 减少了…...

Arduino IDE工程代码多文件编程和中文设置
一、esp8266模块信息 二、中英文切换 点击文件( File )–选择首选项( Preference )—选择语言( Language )—选择中文–点击确定( OK ) 三、多文件编程 在Arduino编程中,将代码分割成多个文件是一种很好的做法,特别是项目变得越来越大和复杂时。这样…...
【微服务】Eureka(服务注册,服务发现)
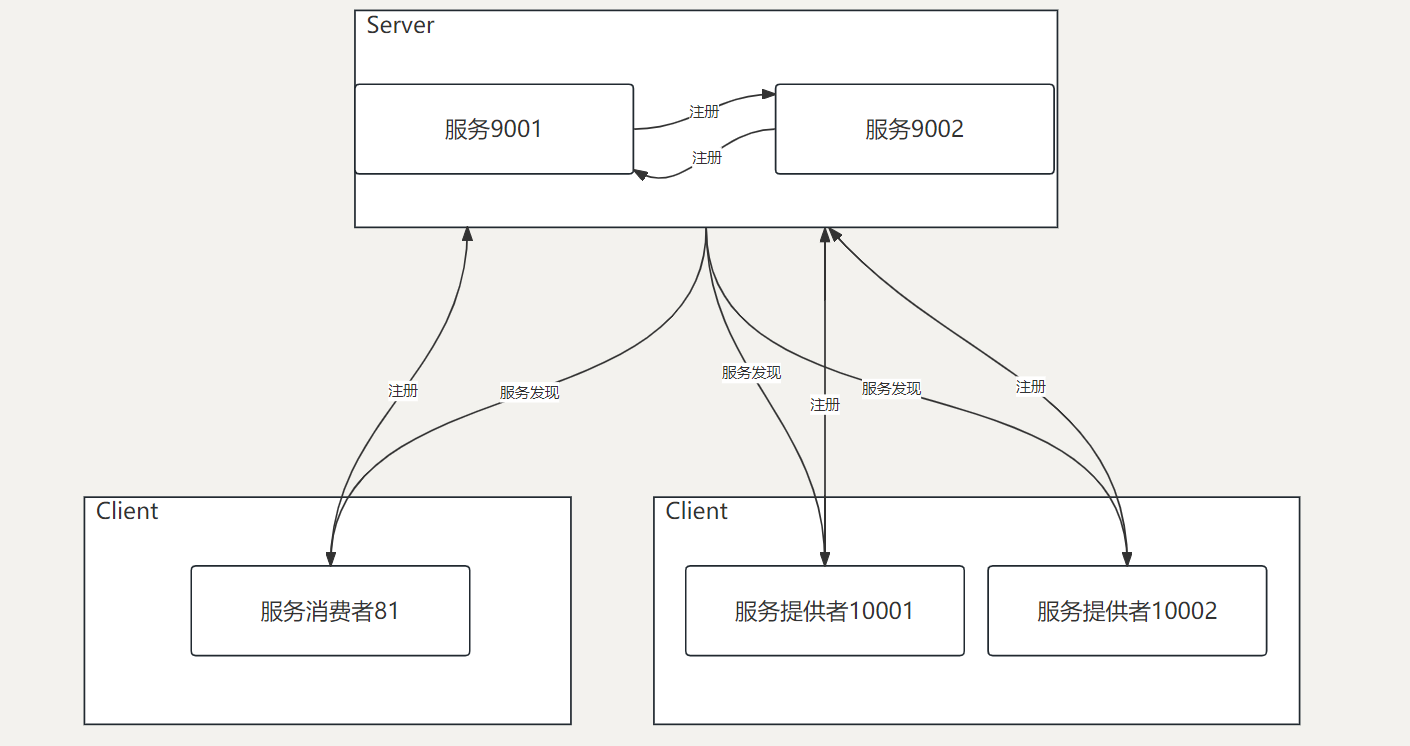
文章目录 1.基本介绍1.学前说明2.当前架构分析1.示意图2.问题分析 3.引出Eureka1.项目架构分析2.上图解读 2.创建单机版的Eureka1.创建 e-commerce-eureka-server-9001 子模块2.检查父子pom.xml1.子 pom.xml2.父 pom.xml 3.pom.xml 引入依赖4.application.yml 配置eureka服务5.…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
