【数据结构与算法】直接插入排序和希尔排序

引言
进入了初阶数据结构的一个新的主题——排序。所谓排序,就是一串记录,按照其中的某几个或某些关键字的大小(一定的规则),递增或递减排列起来的操作。
排序的稳定性:在一定的规则下,两个值相等的元素,在排序算法处理前后的相对位置是否发生变化,如果相对位置变化,称这种排序算法是稳定的,否则为不稳定的。(这个概念并不影响你对排序的学习)
排序将会是初阶数据结构的收尾模块,在这个模块中,将会带领大家学习七大知名的排序方式。而在本篇博客中,将会介绍其中的两个排序,一个是直接插入排序,另一个则是希尔排序。不过在开始我们排序的讲解之前,先介绍一下我们将要讲的排序算法都有哪些。
没错,我们今天将要处理的就是插入排序模块。
直接插入排序
直接插入排序是一种简单的插入排序法,如果想更好的理解希尔排序,首先需要弄懂直接插入排序,其基本思想是:
把待排序的元素按其大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
很像我们打扑克时,别人给你发一副乱序的牌让你自己手动排序的过程(需要从左往右依次排好顺序):

直接插入排序核心逻辑:当你插入第 i 个元素时,前面的 array[0],array[1]……array[i-1] 已经排好序,此时让array[i]的数据按array[i-1]……往前的顺序依次比较,找到可插入的位置插入array[i]。原来位置上的元素顺序后移。
这里博主找了一个动图供大家参考理解: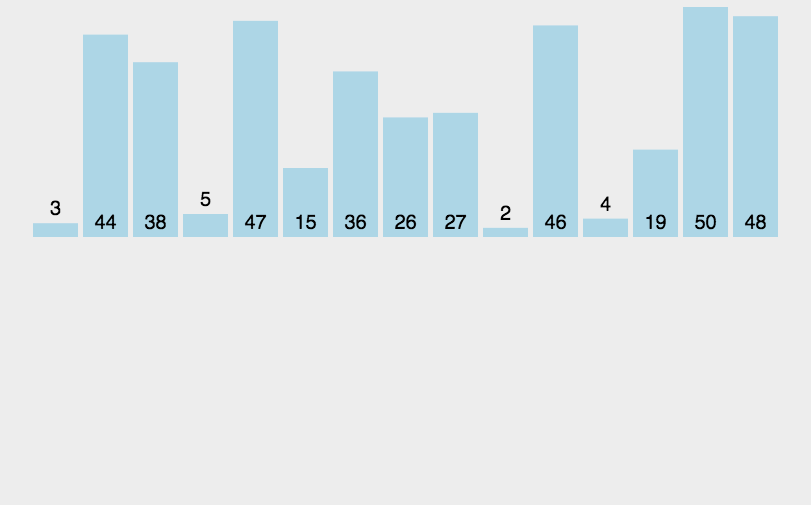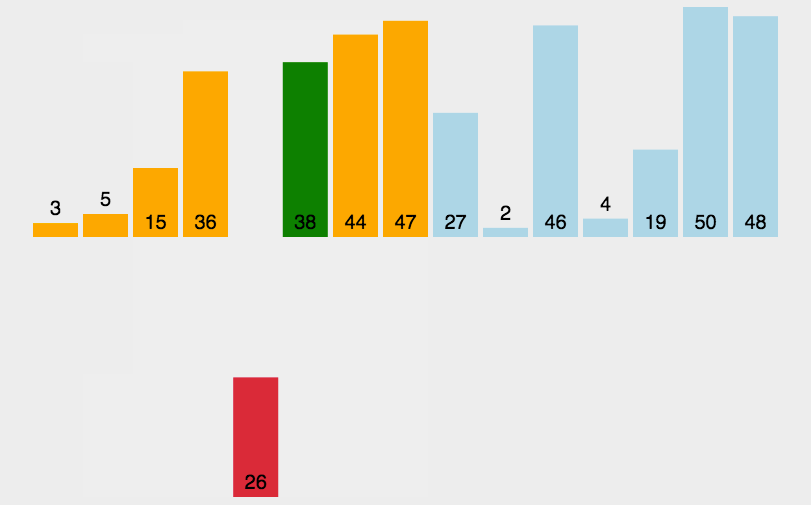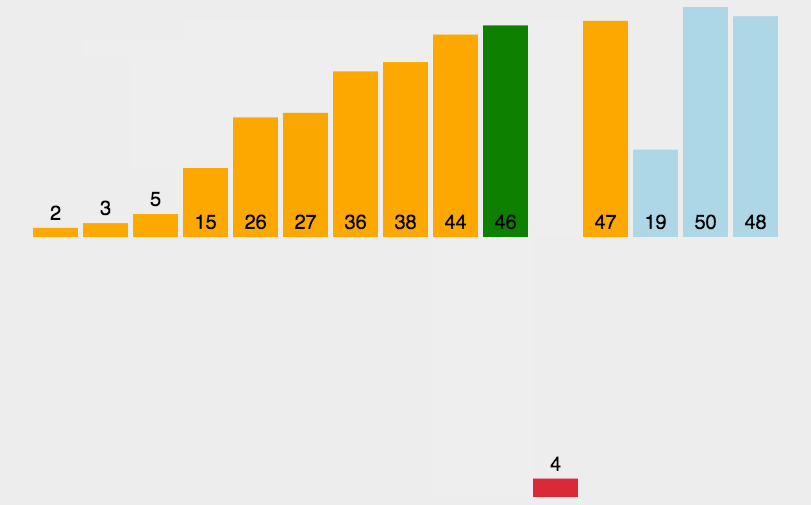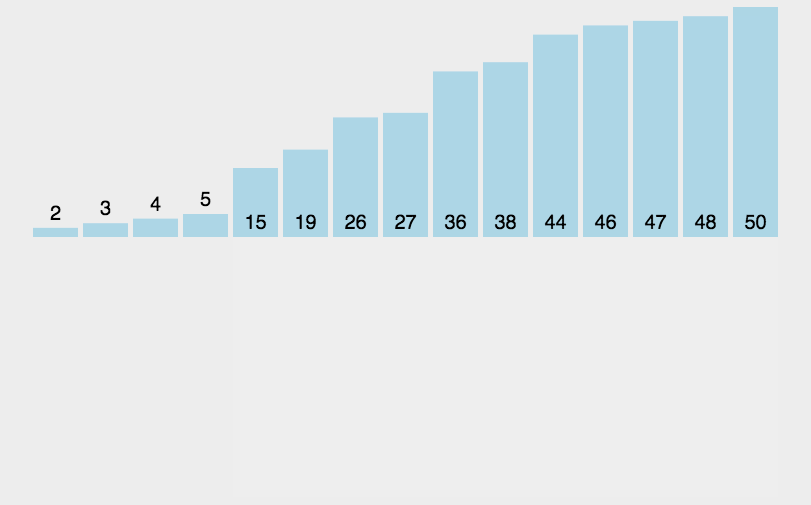
实现直接插入排序
我们可以先来分析一下单趟的直接插入排序,分为两种情况:
1. 单趟排序(单独取一趟排序分析其过程)过程中end走到序列中间即插入,此时tmp小于a[end]
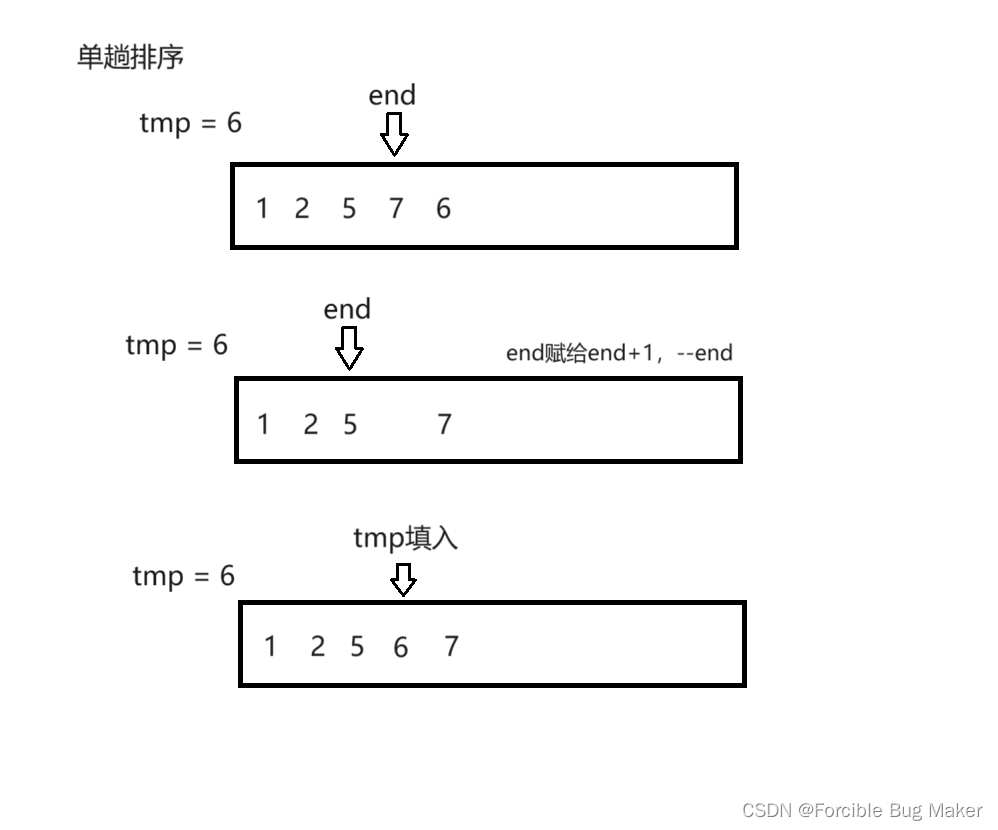
2. [0,end] 区间中元素均小于需插入元素 a[end+1] ,也就是tmp时,单趟排序end走到序列最前面,end == -1

下面是单趟的代码实现:
int end = 3;
int tmp = a[end + 1];
while (end >= 0) {if (tmp < a[end]) {a[end + 1] = a[end];--end;}else break;
}
a[end + 1] = tmp;当end的值从1一直排到末尾序列值n - 2时,整个插入排序便完成了。
for循环遍历 end [0, n - 2] ,由于长度为n的数组有效下标最大为n - 1,当end为n - 1时,要插入的元素tmp存的刚好就是a[end + 1],也就是下标为n - 1的数,同时也就是数组的最后一个值。

直接插入排序代码
// 直接插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++) {// [0,end]区间内有序,end + 1位置是待插入元素int end = i;// tmp保存的是待插入元素的值int tmp = a[end + 1];while (end >= 0) {if (tmp < a[end]) {// 后移元素操作a[end + 1] = a[end];--end;}else break;}//元素的插入a[end + 1] = tmp;}
}直接插入排序的特性:
- 时间复杂度:O(N^2)
- 空间复杂的:O(1)
- 元素越接近有序,直接插入排序算法效率越高。
- 稳定性:稳定
- 最好情况:有序/接近有序
- 最坏境况:逆序
当一个序列接近有序时,每一趟直接插入的过程都会变得简单很多,即往前走上几步便能找到比tmp大的值从而跳出单趟循环,在每一次循环的跳出过程中,直接插入排序的时间复杂度可达 O(N)。相反,当一个排序按逆序排列,每一趟都需要将前面的所有元素往后移动一次插入tmp,时间复杂度便成了计算一个等差数列和:
,其时间复杂度显而易见——O(N^2)。
希尔排序
希尔排序也是插入排序的一种,是一个名叫希尔(Donald Shell)的大佬思考推论得出的排序方式,其底层逻辑本质上来说还是直接插入排序。希尔大佬发现了直接插入排序元素越接近有序,直接插入排序算法效率越高这一特点,突发奇想:直接插入排序在非顺序的元素序列中,如果插入元素的值较小,需要从插入尾部一步步移到头部,这个过程中的消耗无疑是巨大的。如果能有一种方式,能将乱序元素序列通过允许远距离的交换元素进行预排列,快速生成一个接近有序的序列,这时候在调用直接插入排序,排序的速率是否会大大提升。
在希尔排序正真被众人所接受之前,这个排序方式也备受质疑,但时间总会给出答案,希尔排序在现今排序大家庭中有着举足轻重的地位。
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序序列中所有元素分成 i 个组,所有距离为 i 的记录分在同一组内,并对每一组内的元素进行直接插入排序。然后,取 i = n / 2 (n为排序序列元素个数) 重复上述分组和排序的工作。当到达 i = 1 时,所有记录在统一组内排好序。
总结一下其过程:
- 预排序(gap > 1)
- 直接插入排序(gap == 1)
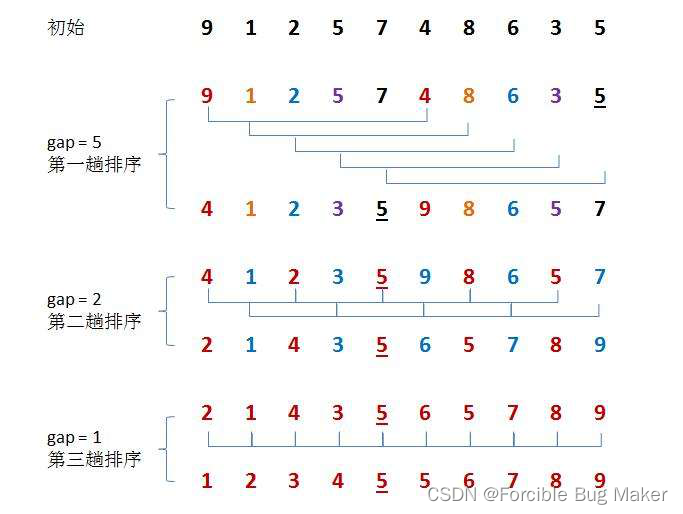
实现希尔排序
我们可以首先来分析一下单趟的希尔排序。
设 gap == 3 的时候:
每隔3个元素取一个数,最后可以分成gap(gap == 3)组数

这时候,将分好的每一组进行排序,排序方式为直接插入排序。注意,在排序的过程中,不同的组之间的位置不会有交集,元素的位置始终实在自己组内变动的。拿上面举例,gap == 3的第一组数只会在0,3,6,9位置上排序,不会将数字排到其他组的位置上。
这里我们可以复用一下之前选择排序的单趟,只不过++变成了+=gap,--变成了-=gap(因为是按照gap分组间隔排序的,不同组需要排序的元素之间间隔都为gap),下面是排单组(第一组:4 8 3 7)元素时的代码。
int gap = 3;
for (int i = 0; i < n - gap; i += gap) {int end = i;int tmp = a[end + gap];while (end >= 0) {if (tmp < a[end]) {a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = tmp;
}这时候,想要排分好的多组元素就会容易非常多了,我们再套一层循环,就可以达到排序不同组的效果。
gap = 3;
for (int rem = 0; rem < gap; rem++) {for (int i = 0; i < n - gap; i += gap) {int end = i;int tmp = a[end + gap];while (end >= 0) {if (tmp < a[end]) {a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = tmp;}
}这里的代码,就成功的达到帮gap的所有组排序的效果了。现在,实现希尔排序就只差最后一步,就是改变gap的值,让其从n / 2,一直除2直到除到1为止,每得到一次gap都进行一次上面的分组排序运算,下面就是完整的希尔排序代码。
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1) {gap = gap / 2;for (int rem = 0; rem < gap; rem++) {for (int i = 0; i < n - gap; i += gap) {int end = i;int tmp = a[end + gap];while (end >= 0) {if (tmp < a[end]) {a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = tmp;}}}
}希尔排序代码
不过,你难道以为希尔排序到这里就结束了?其实这份代码还有优化的空间。比如说,其实你可以省去遍历不同组的for循环,像下面这样。其实本质没什么变化,就是把一组一组拿出来排序的方式改成按顺序在不同组之间换着排。
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1) {gap = gap / 2;//去掉遍历不同组的for循环,下面遍历的i+=gap改为i++for (int i = 0; i < n - gap; i++) { int end = i;int tmp = a[end + gap];while (end >= 0) {if (tmp < a[end]) {a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = tmp;}}
}你还可以将gap = gap / 2 改成gap = gap / 3 + 1。
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1) {gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++) {int end = i;int tmp = a[end + gap];while (end >= 0) {if (tmp < a[end]) {a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = tmp;}}
}关于希尔排序的一些特性和问题
不过对于gap的取法其实很多,最初Shell提出gap = gap / 2,后来Knuth提出取 gap = (gap / 3) + 1,还有人提出取奇数或者是互质更好。但无论哪一种主张都没有得到证明。
《数据结构-用面相对象方法与C++描述》--- 殷人昆

希尔排序的特性:
- 时间复杂度:希尔排序的时间复杂度不好计算,gap的取值方法很多,导致很难去计算,在好些书中给出的希尔排序的时间复杂度都不固定。Knuth经过大量的实验统计,复杂度大概在O(n^1.25)~O(1.6*n^1.25)之间。现代更高效的增量序列可以使希尔排序达到O(N*logN)的复杂度。
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。整体而言,可以达到优化的效果。
- 稳定性:不稳定
《数据结构(C语言版)》--- 严蔚敏

测试计算效果
clock()函数是<time.h>头文件中的一个函数,用来返回程序启动到函数调用之间的CPU时钟周期数。这个主可以用来帮助我们衡量程序或程序某个部分的性能。
我们可以计算对比一下本篇博客两个排序方式占用的CPU时间
void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);}上面这段代码的功能是生成十万个随机数,分别用希尔排序和直接插入排序去排列,同时用clock记录所消耗的时间,打印结果。
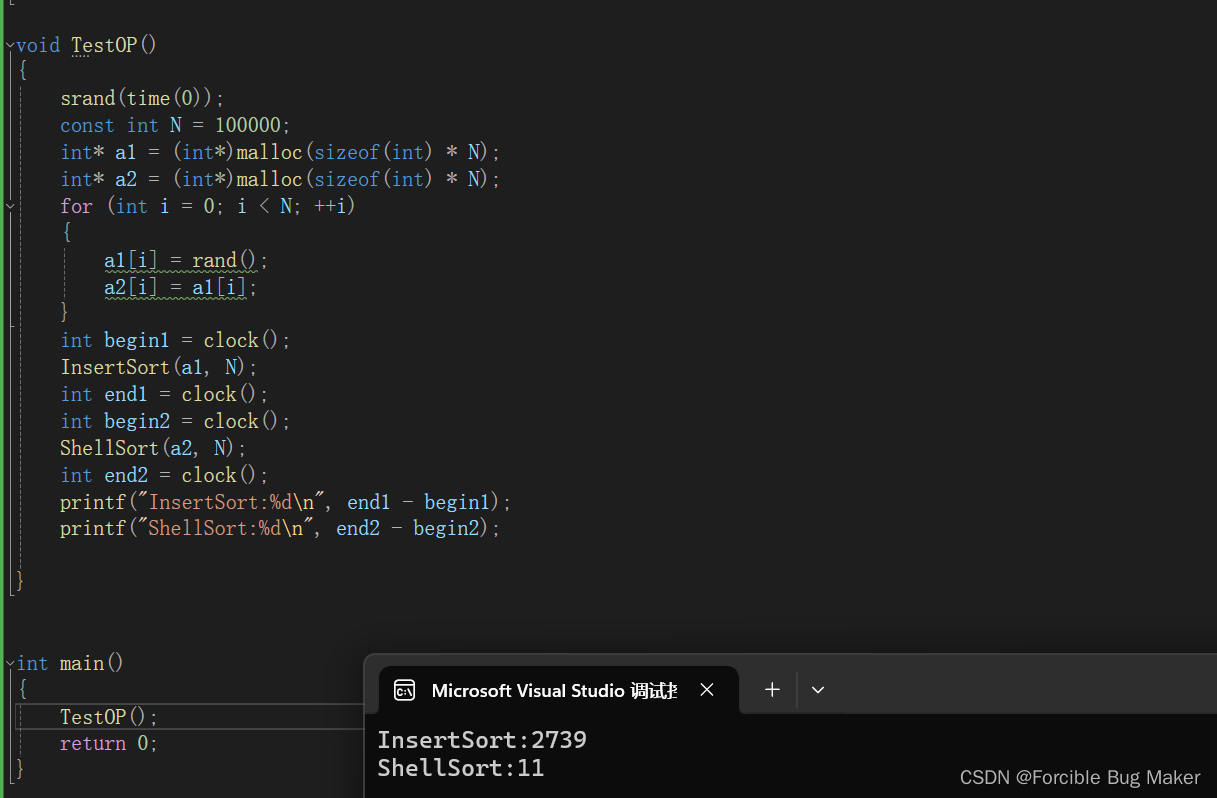
我们可以发现希尔排序相比于直接插入排序的性能提升了很多。
结语
本篇博客的内容到这里就结束了,插入排序的序列元素越接近有序,直接插入排序算法效率越高。希尔正是发现了其特点,引入“增量”的概念,允许排序中远距离的交换元素,快速达到预排序效果,大幅度提高了对大规模数据集的排序效率。直接插入排序和希尔排序在计算机科学的排序算法领域中占有重要地位。在掌握其中规律之后,相信你对排序一定有了更加深入的理解。
相关文章:

【数据结构与算法】直接插入排序和希尔排序
引言 进入了初阶数据结构的一个新的主题——排序。所谓排序,就是一串记录,按照其中的某几个或某些关键字的大小(一定的规则),递增或递减排列起来的操作。 排序的稳定性:在一定的规则下,两个值…...

HQL,SQL刷题,尚硅谷
目录 相关表数据: 题目及思路解析: 多表连接 1、课程编号为"01"且课程分数小于60,按分数降序排列的学生信息 2、查询所有课程成绩在70分以上 的学生的姓名、课程名称和分数,按分数升序排列 3、查询该学生不同课程的成绩…...

随机生成用户名、密码、注册时间【Excel】
1.1简介 最近想虚拟一些数据,看下有没有自动生成的工具。百度看了下,大概有这么几种方法 1.excel内置公式函数处理 2.使用使用VBA宏生成随机 3.下载方方格子,emm工具是个好工具,蛮多功能的,每月8块 4.Java函数实现…...

C++函数模板详解(结合代码)
目录 1. 模板概念 2. 函数模板语法 3. 函数模板注意事项 4. 函数模板案例 5. 普通函数与函数模板的区别 6. 普通函数与函数模板的调用规则 7. 模板的局限性 1. 模板概念 在C中,模板是一种通用的程序设计工具,它允许我们处理多种数据类型而不是固…...

Nest学习随笔
一、Middleware(中间件)、Interceptor(拦截器)、ExceptionFilter(异常过滤器) 执行顺序 接口调用正常:Middleware > Interceptor接口调用异常:Middleware > ExceptionFilter 二、访问静态文件 使用 nestjs/serve-static 依赖 配置方法&#x…...
二十二、软考-系统架构设计师笔记-真题解析-2018年真题
软考-系统架构设计师-2018年上午选择题真题 考试时间 8:30 ~ 11:00 150分钟 1.在磁盘调度管理中,应先进行移臂调度,再进行旋转调度。假设磁盘移动臂位于21号柱面上,进程的请求序列如下表所示。如果采用最短移臂调度算法,那么系统…...

2024最新最全Selenium自动化测试面试题!
1、什么是自动化测试、自动化测试的优势是什么? 通过工具或脚本代替手工测试执行过程的测试都叫自动化测试。 自动化测试的优势: 1、减少回归测试成本 2、减少兼容性测试成本 3、提高测试反馈速度 4、提高测试覆盖率 5、让测试工程师做更有意义的…...
Docker 搭建Redis集群
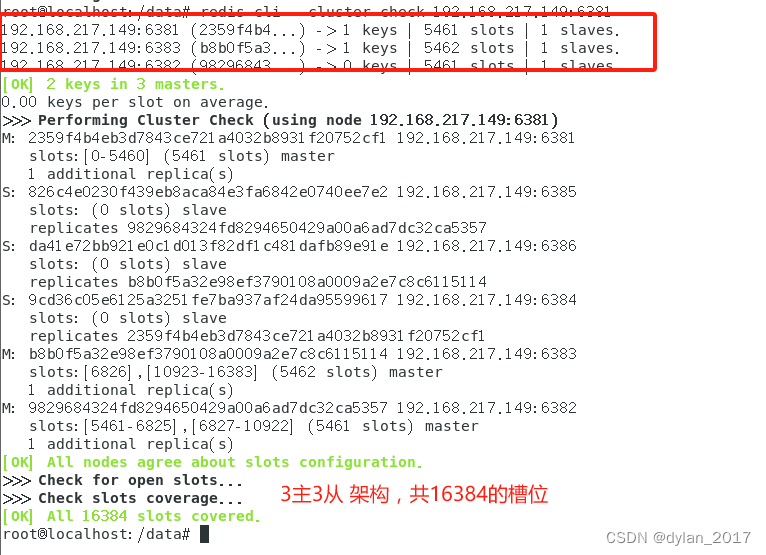
目录 1. 3主3从架构说明 2. 3主3从Redis集群配置 2.1关闭防火墙启动docker后台服务 2.2 新建6个docker容器实例 2.3 进去任意一台redis容器,为6台机器构建集群关系 2.4 进去6381,查看集群状态 3. 主从容错切换迁移 3.1 数据读写存储 3.1.1 查看…...
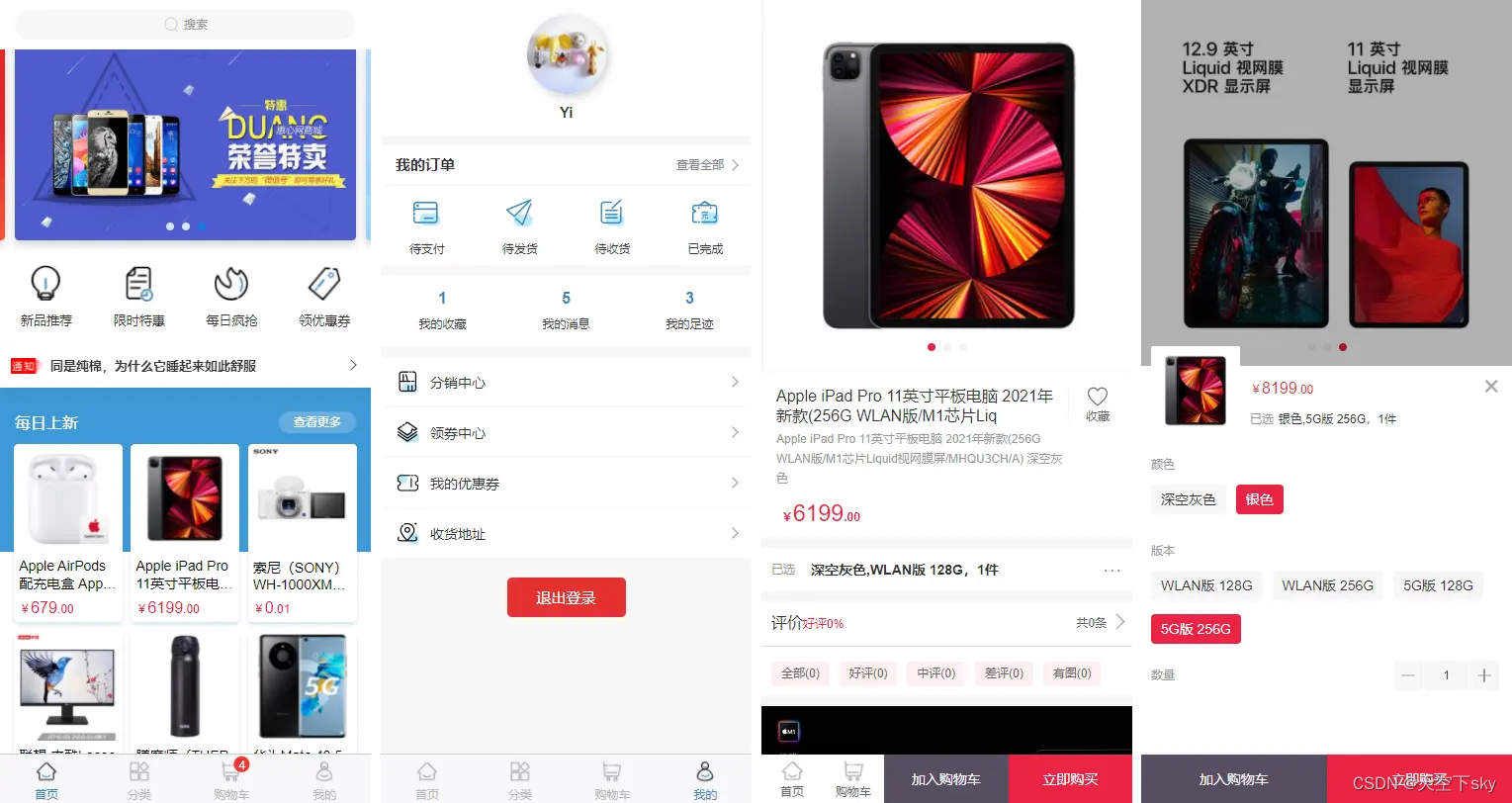
spring boot商城、商城源码 欢迎交流
一个基于spring boot、spring oauth2.0、mybatis、redis的轻量级、前后端分离、防范xss攻击、拥有分布式锁,为生产环境多实例完全准备,数据库为b2b2c设计,拥有完整sku和下单流程的商城 联系: V-Tavendor...

全面解析“通义千问”:功能、优势与使用指南
引言: “通义千问”是由阿里云研发的一款先进的人工智能语言模型,以其强大的自然语言处理能力与广泛的知识覆盖面,在教育、咨询、信息检索等领域发挥着重要作用。本文将详细介绍“通义千问”的核心功能、显著优势以及具体使用方法。 一、“…...

【第三方登录】Google邮箱
登录谷歌邮箱开发者 https://console.developers.google.com/ 先创建项目 我们用的web应用 设置回调 核心主要: 1.创建应用 2.创建客户端ID 3.设置域名和重定向URL 4.对外公开,这样所有的gmail邮箱 都能参与测试PHP代码实现 引入第三方包 h…...

oslo_config学习小结
2.配置文件加载方法 2.1基础 配置文件指的是文件以.conf,.ini结尾等内容为配置项的文件,配置文件内容格式一般为 [DEFAULT] option value [sectiona] optiona valuea optionb valueb [sectionb] optionc valuec optiond valued 2.2加载方法…...
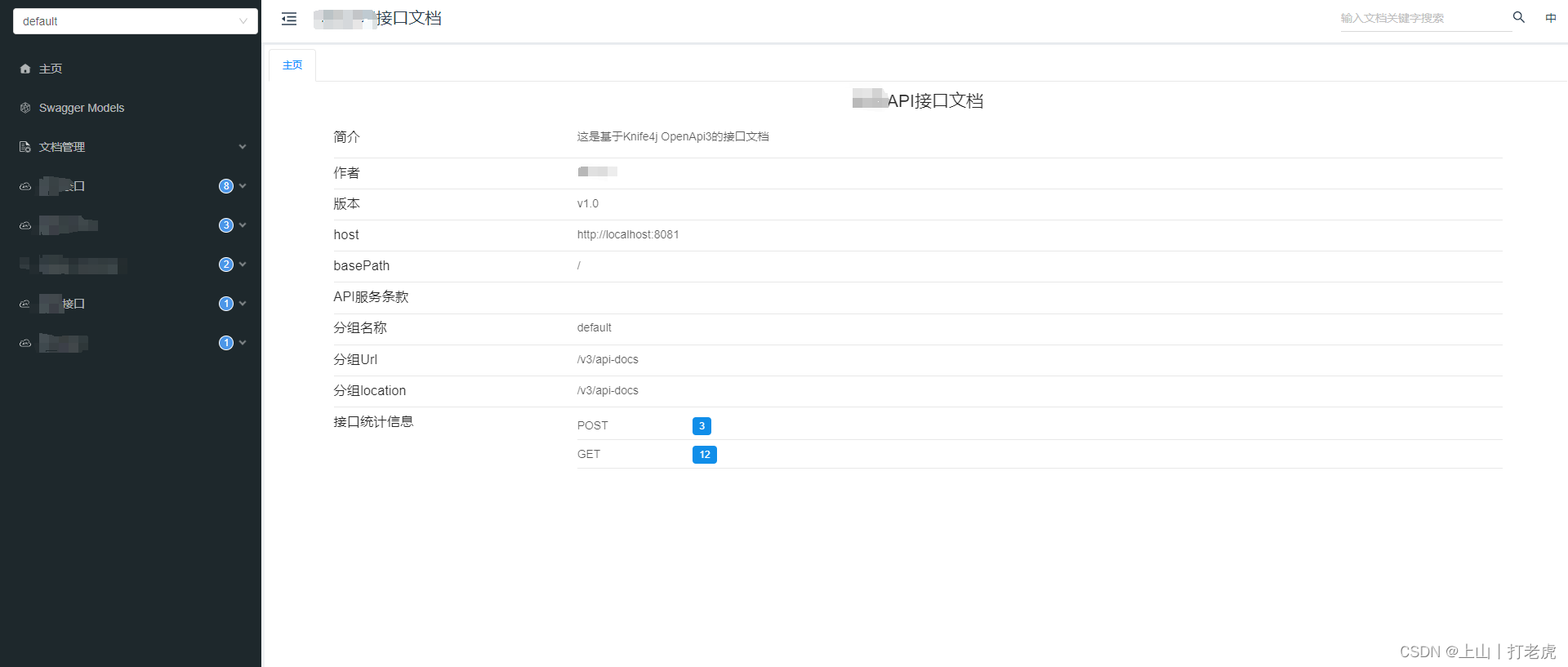
SpringBoot2.6.3 + knife4j-openapi3
1.引入项目依赖: <dependency><groupId>com.github.xiaoymin</groupId><artifactId>knife4j-openapi3-spring-boot-starter</artifactId><version>4.5.0</version> </dependency> 2.新增配置文件 import io.swag…...

PostgreSQL FDW(外部表) 简介
1、FDW: 外部表 背景 提供外部数据源的透明访问机制。PostgreSQL fdw(Foreign Data Wrapper)是一种外部访问接口,可以在PG数据库中创建外部表,用户访问的时候与访问本地表的方法一样,支持增删改查。 而数据则是存储在外部,外部可以是一个远程的pg数据库或者其他数据库(…...
Java项目:75 springboot房产销售系统
作者主页:源码空间codegym 简介:Java领域优质创作者、Java项目、学习资料、技术互助 文中获取源码 项目介绍 使用房产销售系统分为管理员和用户、销售经理三个角色的权限子模块。 管理员所能使用的功能主要有:首页、个人中心、用户管理、销…...
2.6 IDE(集成开发环境)是什么
IDE(集成开发环境)是什么 IDE 是 Integrated Development Environment 的缩写,中文称为集成开发环境,用来表示辅助程序员开发的应用软件,是它们的一个总称。 通过前面章节的学习我们知道,运行 C 语言&…...

tomcat和web服务器是什么??
一、什么是服务器 1.服务器是计算机的一种,它比普通计算机运行更快、负载更高。服务器拥有独立IP地址,并且运行了服务器软件。 2.服务器由服务器软件和服务器硬件组成。服务器硬件就是拥有独立ip的计算机,服务器软件是一个被动的软件&#…...
鸿蒙Harmony跨模块交互
1. 模块分类介绍 鸿蒙系统的模块一共分为四种,包括HAP两种和共享包两种 HAP(Harmony Ability Package) Entry:项目的入口模块,每个项目都有且只有一个。feature:项目的功能模块,内部模式和En…...
由浅到深认识Java语言(30):集合
该文章Github地址:https://github.com/AntonyCheng/java-notes 在此介绍一下作者开源的SpringBoot项目初始化模板(Github仓库地址:https://github.com/AntonyCheng/spring-boot-init-template & CSDN文章地址:https://blog.c…...
Python学习笔记(二)
一:异常: 1.1:异常处理: 1.2:异常捕获: 1.3:异常传递: 二:模块: 2.1:模块的定义: 2.2:模块的导入: 2.3&…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...
