【排序算法】深入解析快速排序(霍尔法三指针法挖坑法优化随机选key中位数法小区间法非递归版本)

文章目录
- 📝快速排序
- 🌠霍尔法
- 🌉三指针法
- 🌠挖坑法
- ✏️优化快速排序
- 🌠随机选key
- 🌉三位数取中
- 🌠小区间选择走插入,可以减少90%左右的递归
- 🌉 快速排序改非递归版本
- 🚩总结
📝快速排序
快速排序是一种分治算法。它通过一趟排序将数据分割成独立的两部分,然后再分别对这两部分数据进行快速排序。
本文将用3种方法实现:
🌠霍尔法
霍尔法是一种快速排序中常用的单趟排序方法,由霍尔先发现。
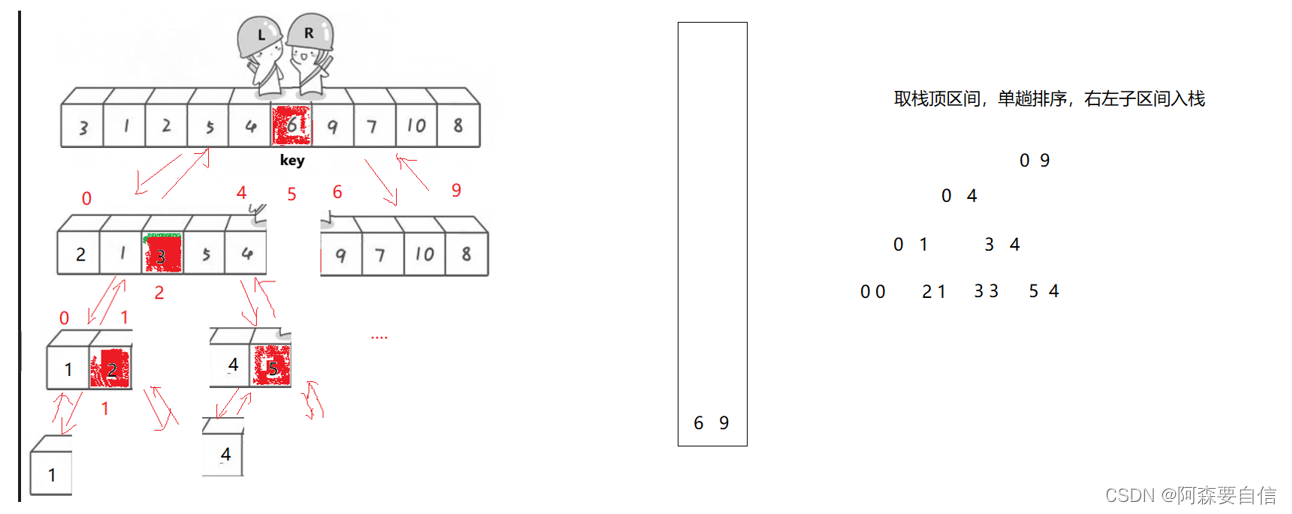
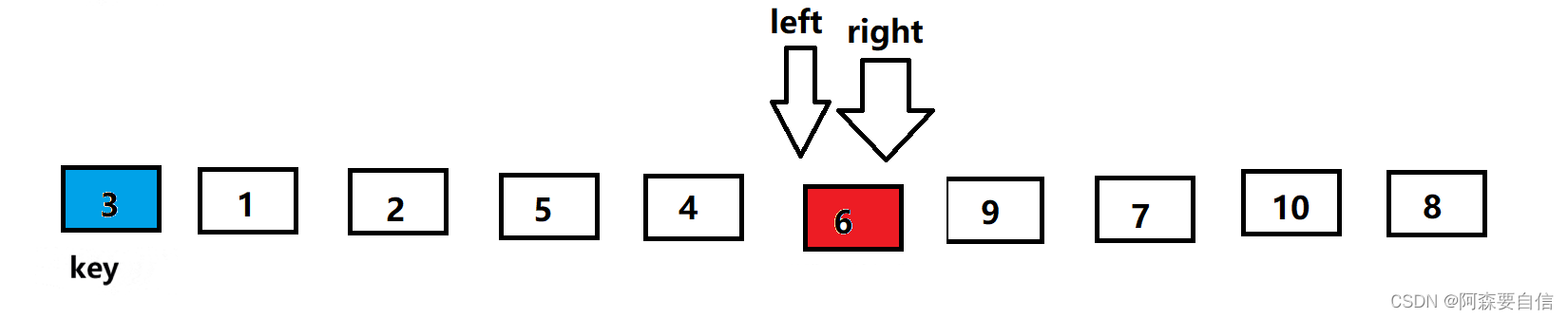
它通过选定一个基准数key(通常是第一个元素),然后利用双指针left和right的方式进行排序,right指针先找比key基准值小的数,left然后找比key基准值大的数,找到后将两个数交换位置,同时实现大数右移和小数左移,当left与right相遇就排序完成,然后将下标key的值与left交换,返回基准数key的下标,完成了单趟排序。这一过程使得基准数左侧的元素都比基准数小,右侧的元素都比基准数大。
如图动图展示:
以下是单趟排序的详解图解过程:
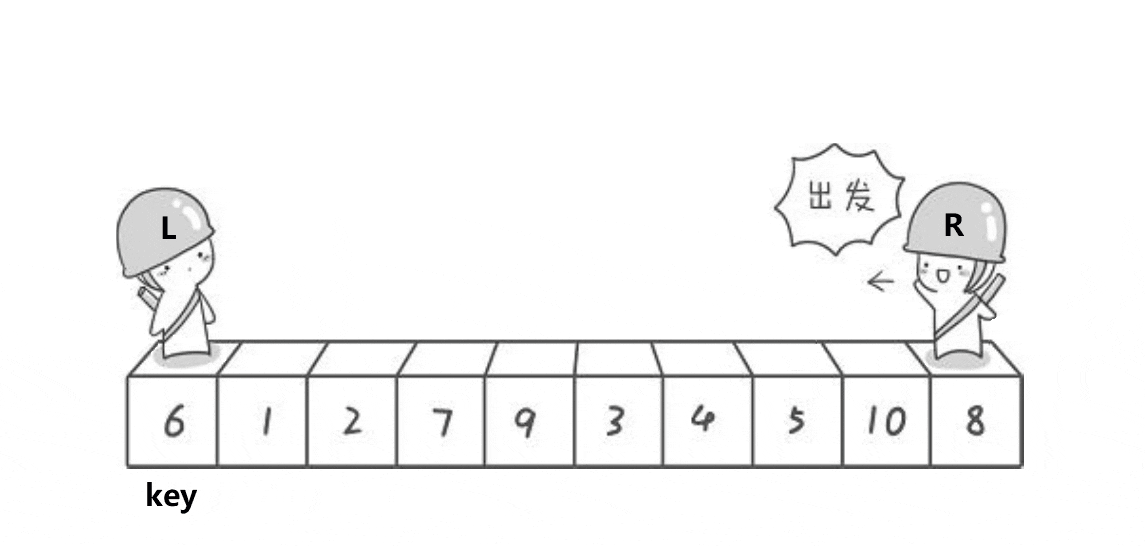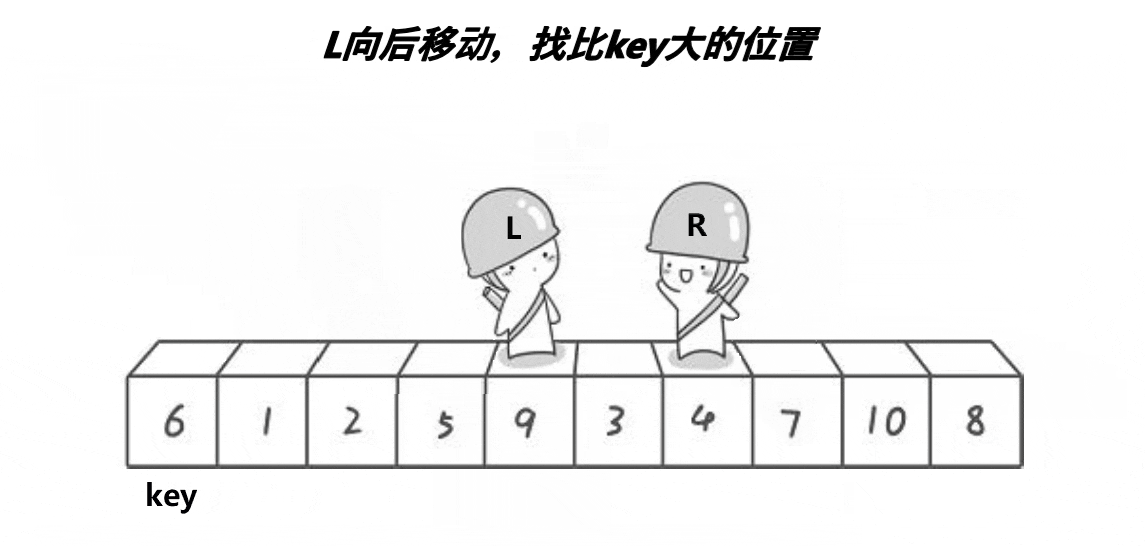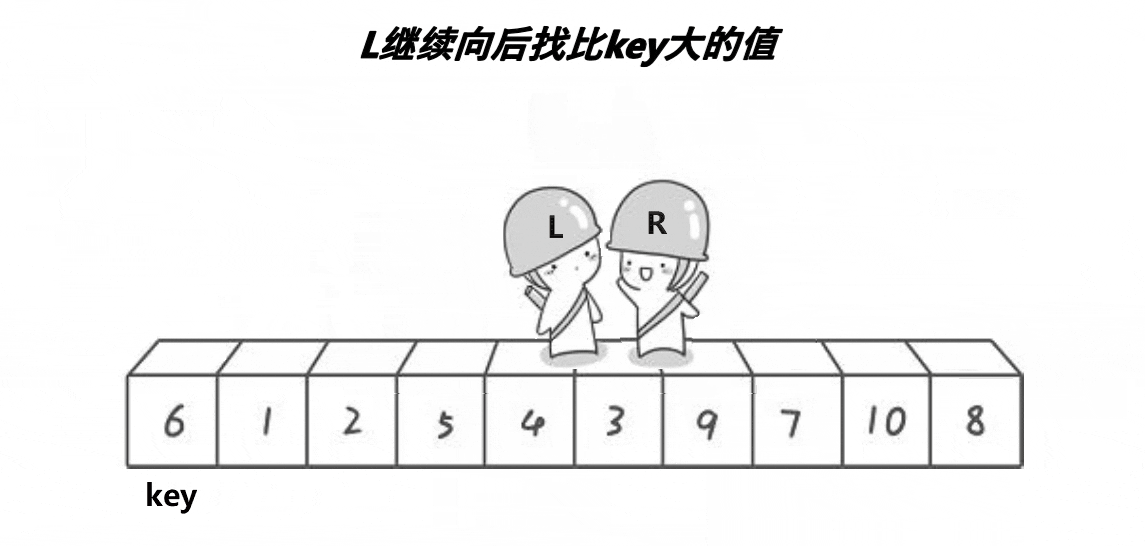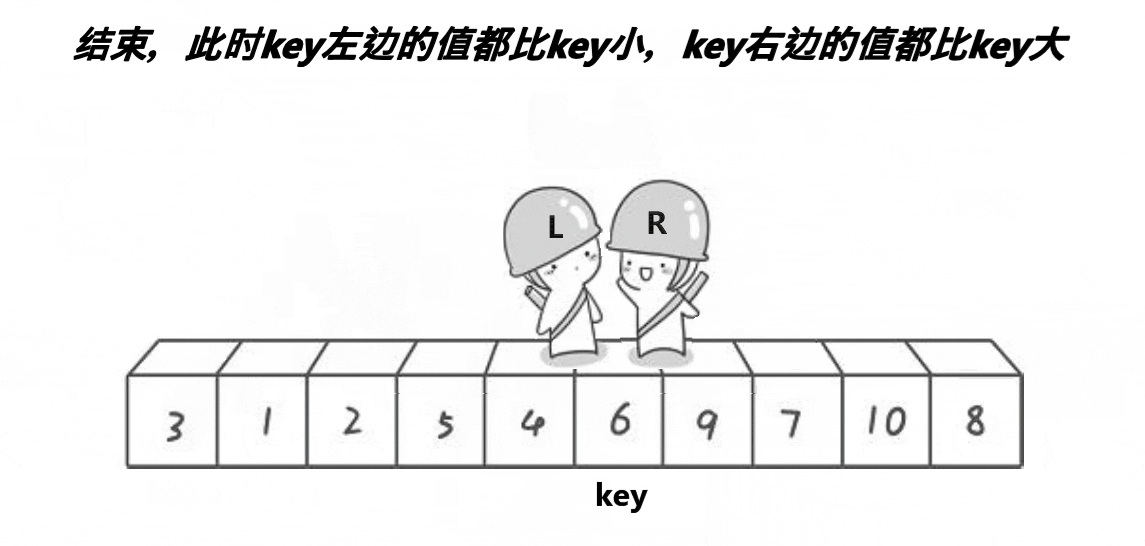
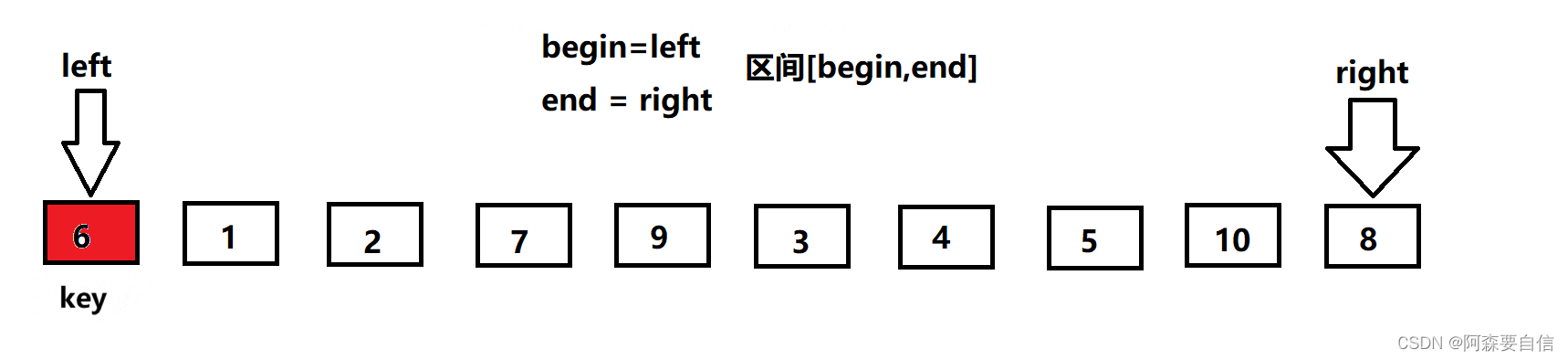
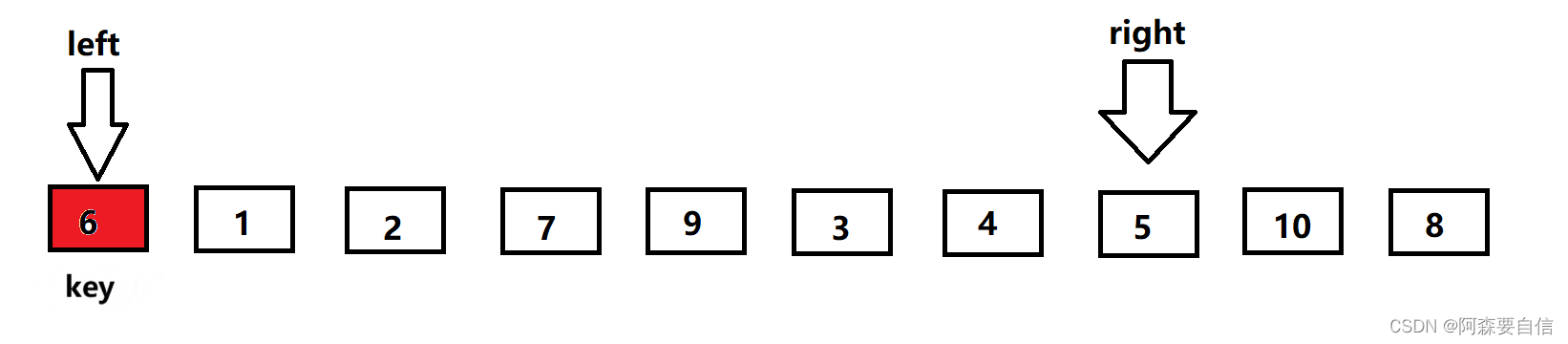
begin和end记录区间的范围,left记录做下标,从左向右遍历,right记录右下标,从右向左遍历,以第一个数key作为基基准值
- 先让
right出发,找比key值小的值,找到就停下来
- 然后
left再出发,找比key大的值,若是找到则停下来,与right的值进行交换
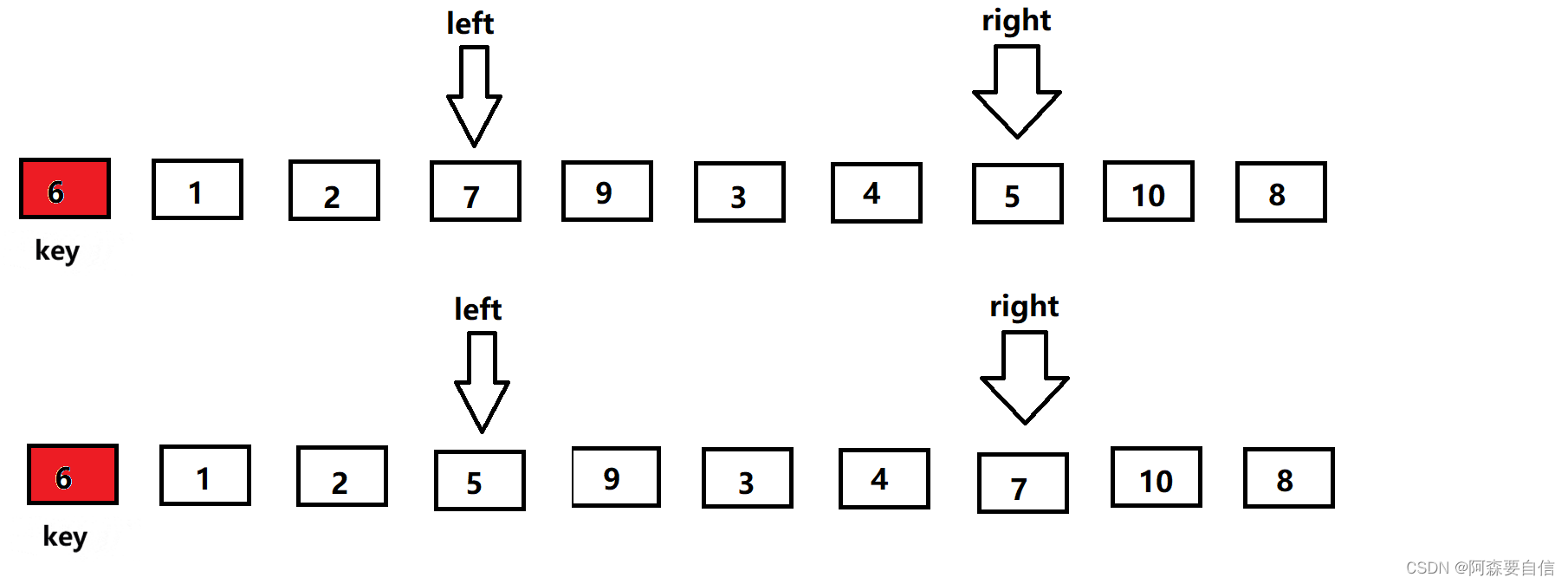
- 接着
right继续找key小的值,找到后才让left找比key大的值,直到left相遇right,此时left会指向同一个数
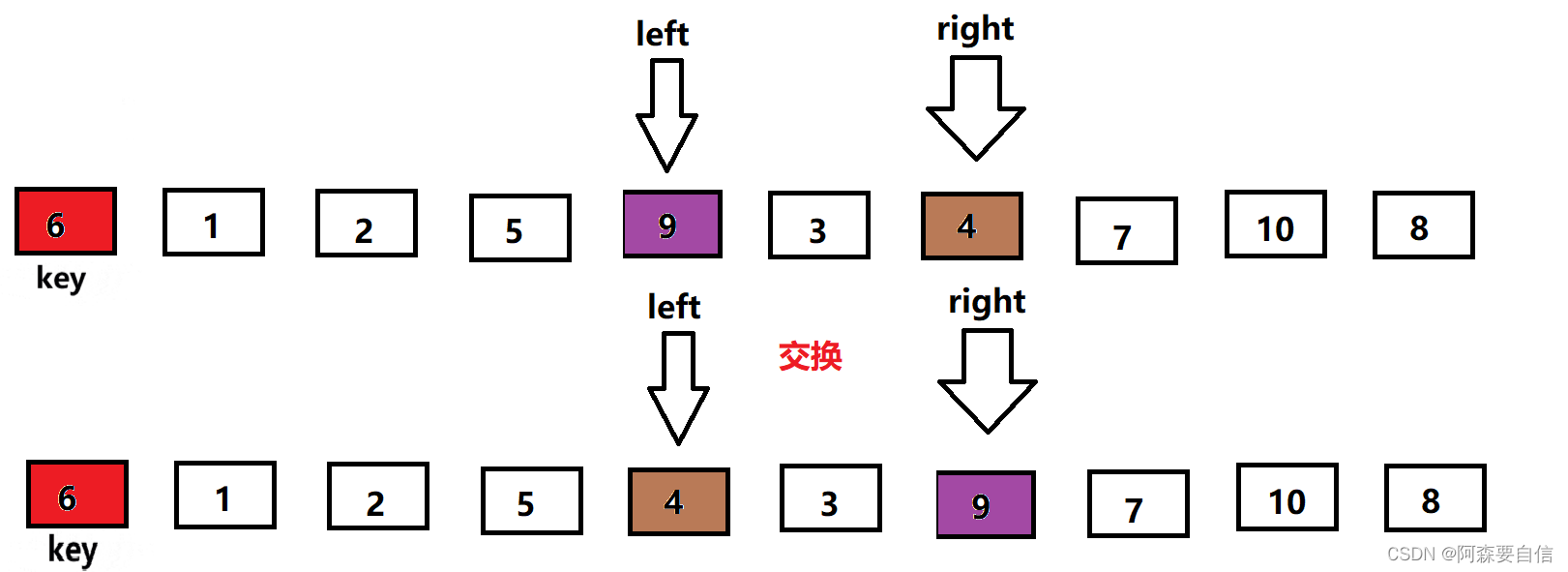
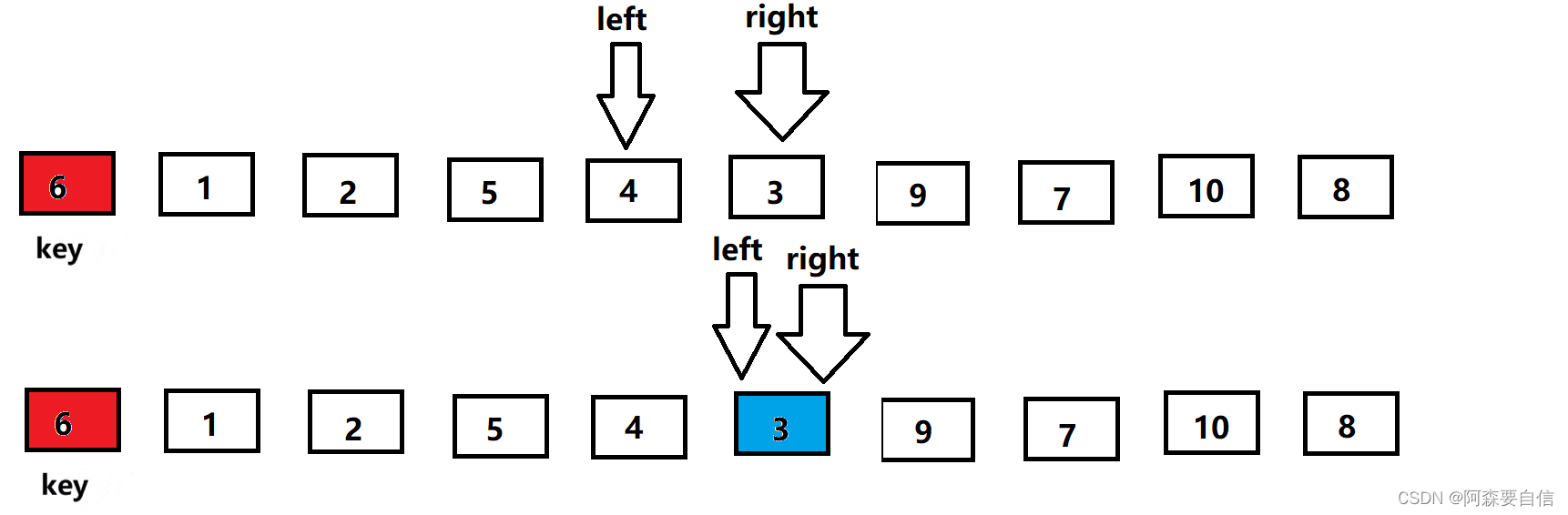
- 将
left与right指向的数与key进行交换,单趟排序就完成了,最后将基准值的下标返回
为啥相遇位置比key要小->右边先走保证的
L遇R:R先走,R在比key小的位置停下来了,L没有找到比key大的,就会跟R相遇相遇位置R停下的位置,是比key小的位置R遇L:第一轮以后的,先交换了,L位置的值小于key,R位置的值大于key,R启动找小,没有找到,跟L相遇了,相遇位置L停下位置,这个位置比key小
- 第一轮
R遇L,那么就是R没有找到小的,直接就一路左移,遇到L,也就是key的位置
代码实现
void Swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}//Hoare经典随机快排
void QuickSort1(int* a, int left, int right)
{// 如果左指针大于等于右指针,表示数组为空或只有一个元素,直接返回if (left >= right)return;// 区间只有一个值或者不存在就是最小子问题int begin = left, end = right;// begin和end记录原始整个区间// keyi为基准值下标,初始化为左指针int keyi = left;// 循环从left到rightwhile (left < right){// right先走,找小,这里和下面的left<right一方面也是为了防止,right一路走出区间,走到left-1越界while (left<right && a[right] >= a[keyi]){--right;}// 左指针移动,找比基准值大的元素 while (left<right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}// 交换左右指针所指元素Swap(&a[left], &a[keyi]);// 更新基准值下标keyi = left;// 递归排序左右两部分//[begin , keyi-1]keyi[keyi+1 , end]QuickSort1(a, begin, keyi - 1);QuickSort1(a, keyi + 1, end);}
🌉三指针法
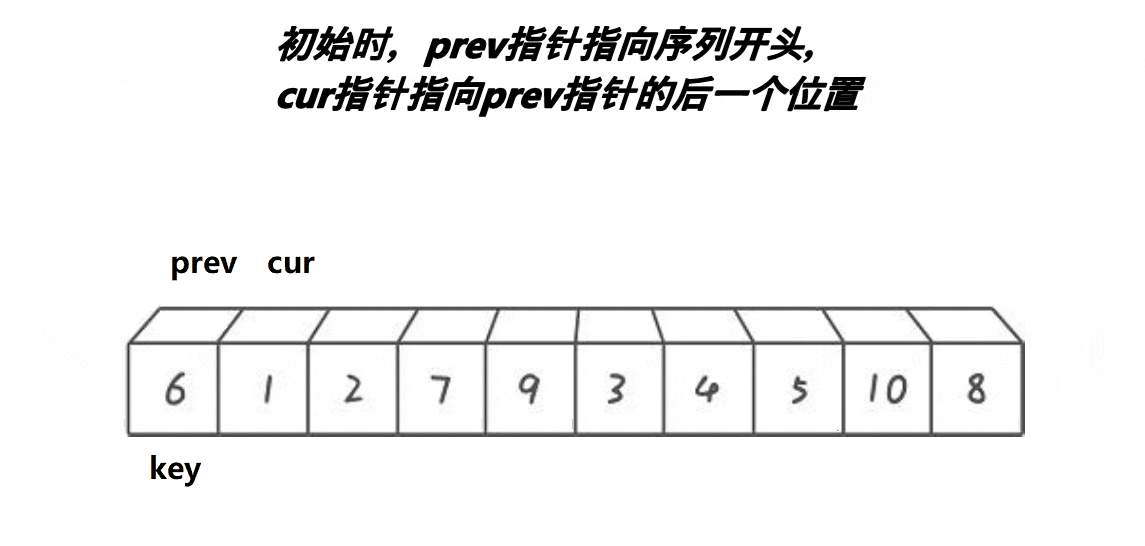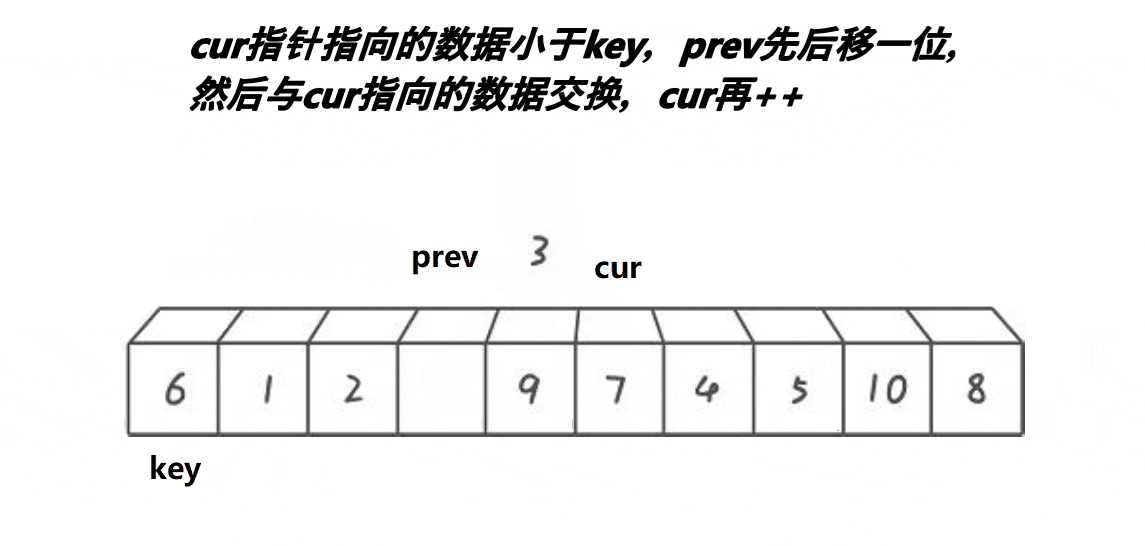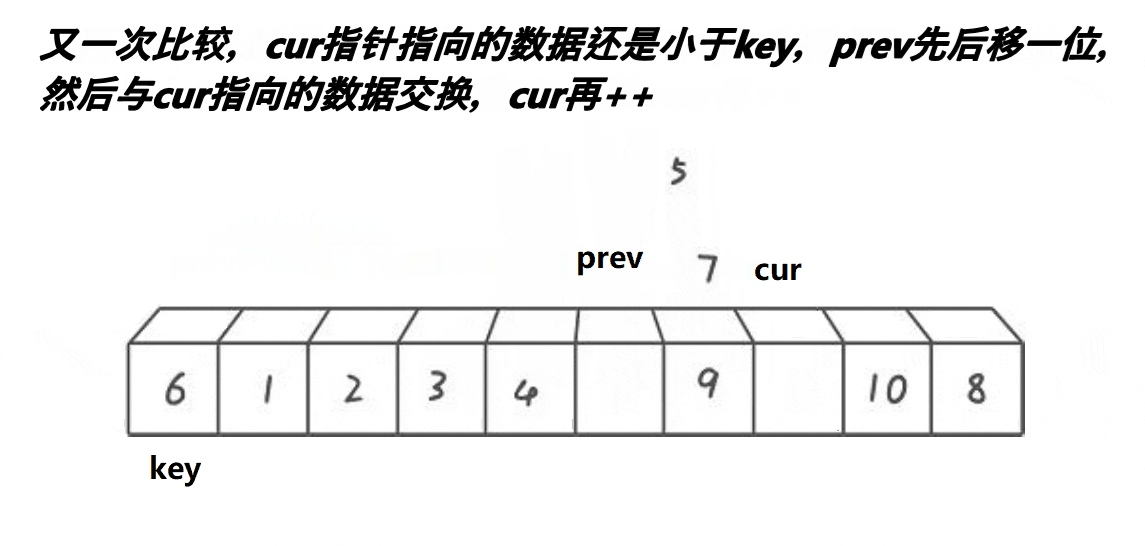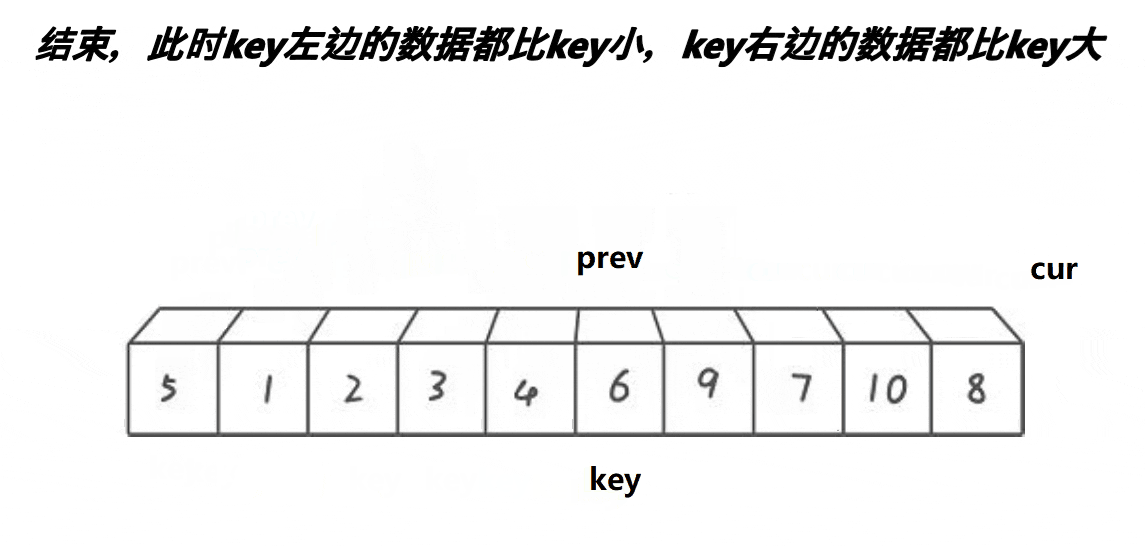
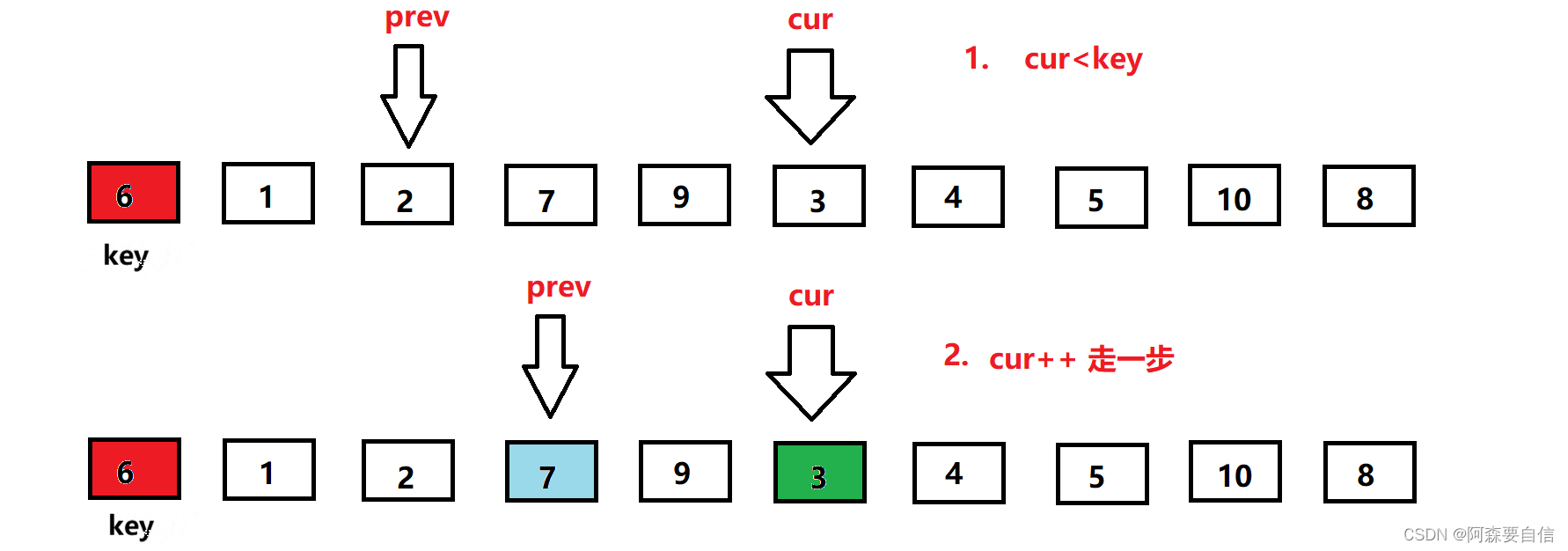
定义一个数组,第一个元素还是key基准值,定义前指针prev指向第一个数,后指针cur指向第二个数,让cur走,然后遍历数组,cur找到大于等于key基准值的数,cur++让cur向前走一步。当cur指针小于key基准值时,后指针加一走一步(++prev),然后交换prev和cur所指的值进行交换,因为这样cur一直都是小于key的值,让他继续向前不断找大的,而prev一直在找小的。依次类推,到cur遍历完数组,完成单趟排序。
如此动图理解:
简单总结:

以下是单趟排序的详解图解过程:
-
一开始,让
prev指向第一个数,cur指向prev的下一位,此时cur位置的数比key基准值小,所以prev加一后,与cur位置的数交换,由于此时prev+1 == cur,自己跟自己交换,交换没变,完了让cur++走下一个位置。
紧接着:
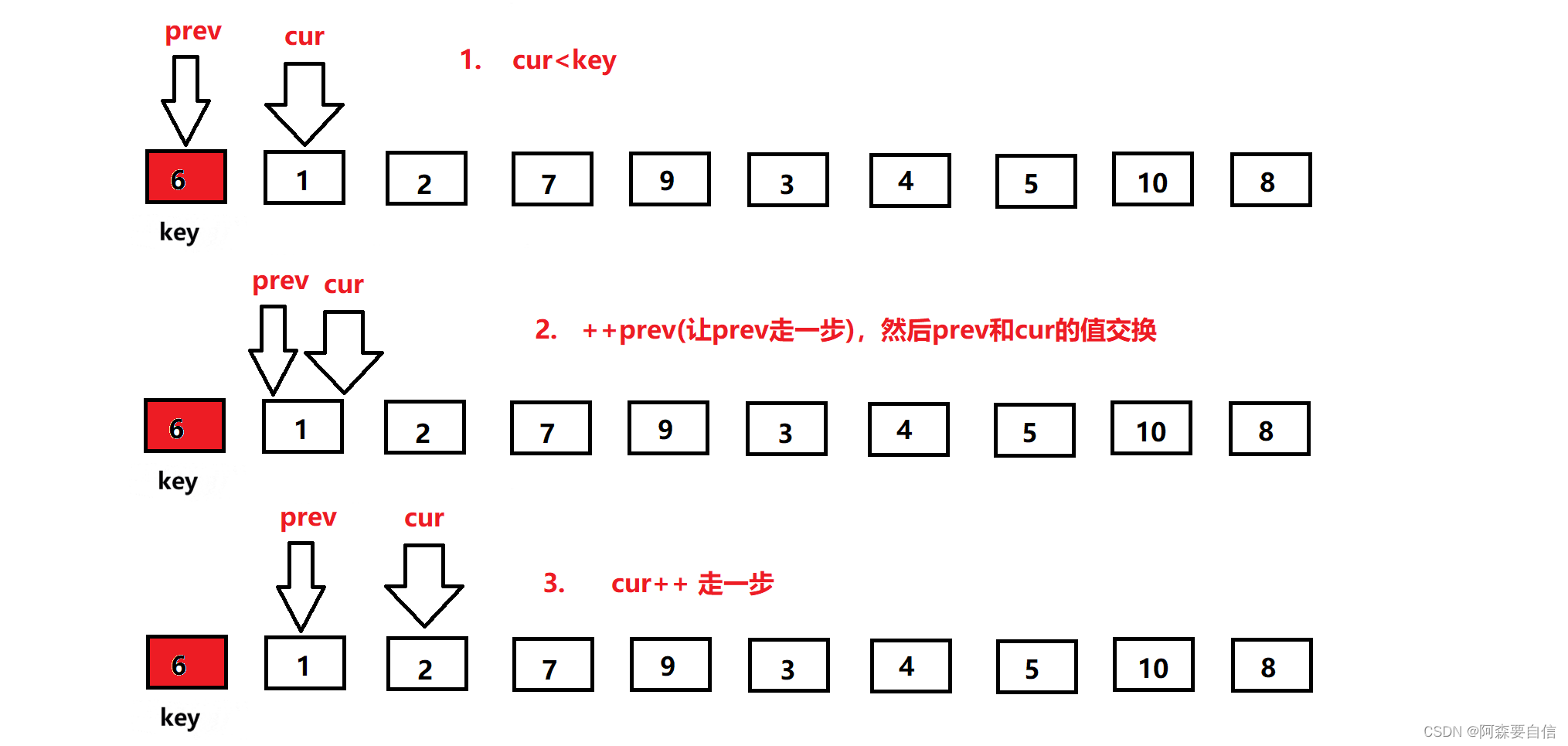
-
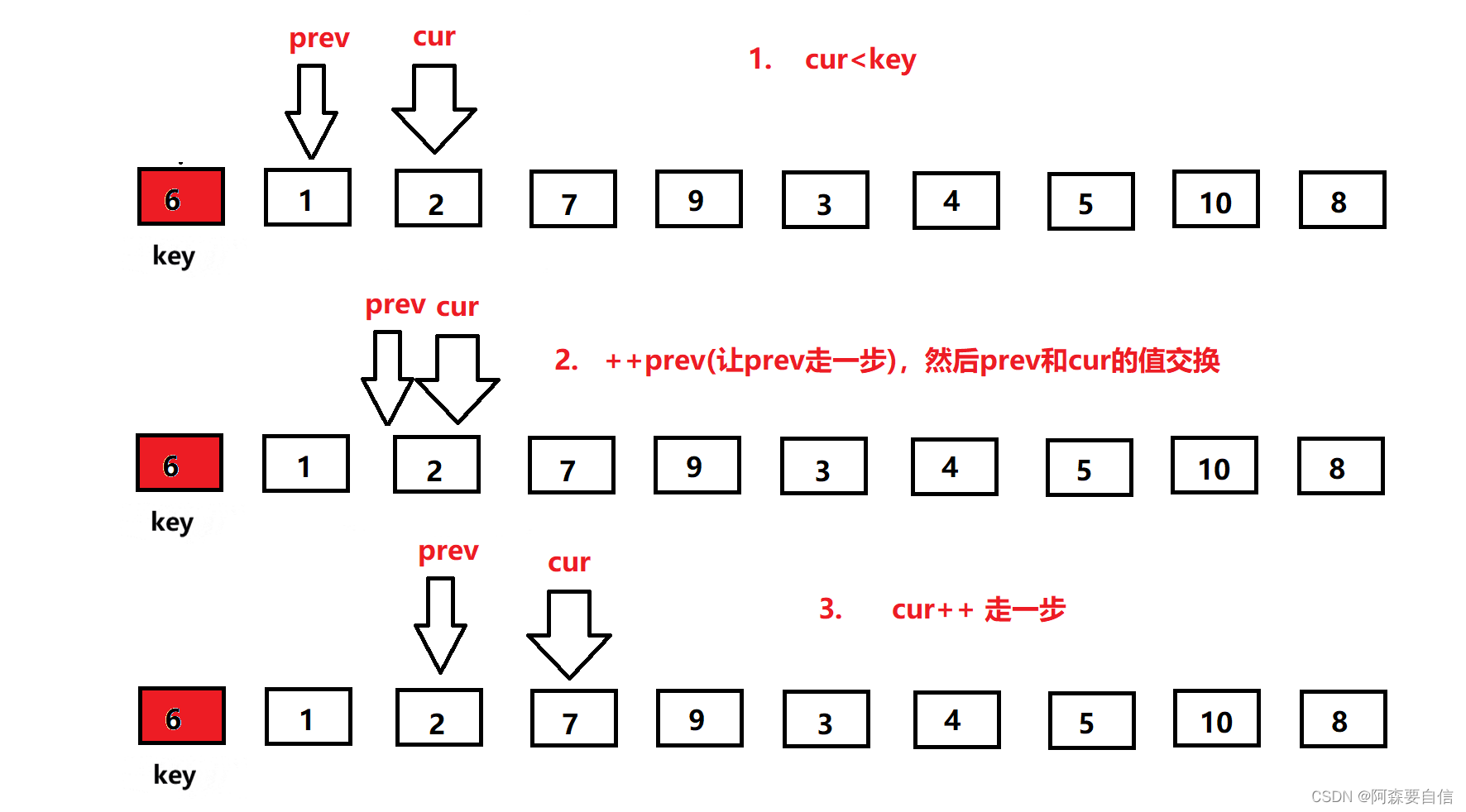
cur继续前进,此时来到了7的位置,大于key的值6,cur++继续向前走,来到9位置,9还是大于6,OK ! 我cur再cur++,来到3的位置,也是看到cur与prev拉开了距离,所以他又叫前后指针,这就体现出来,往下看–》

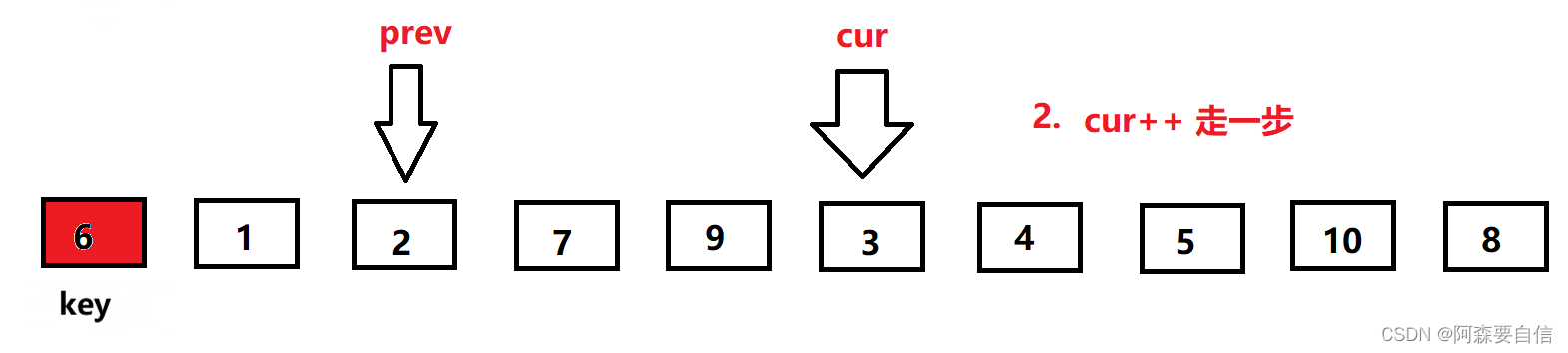
-
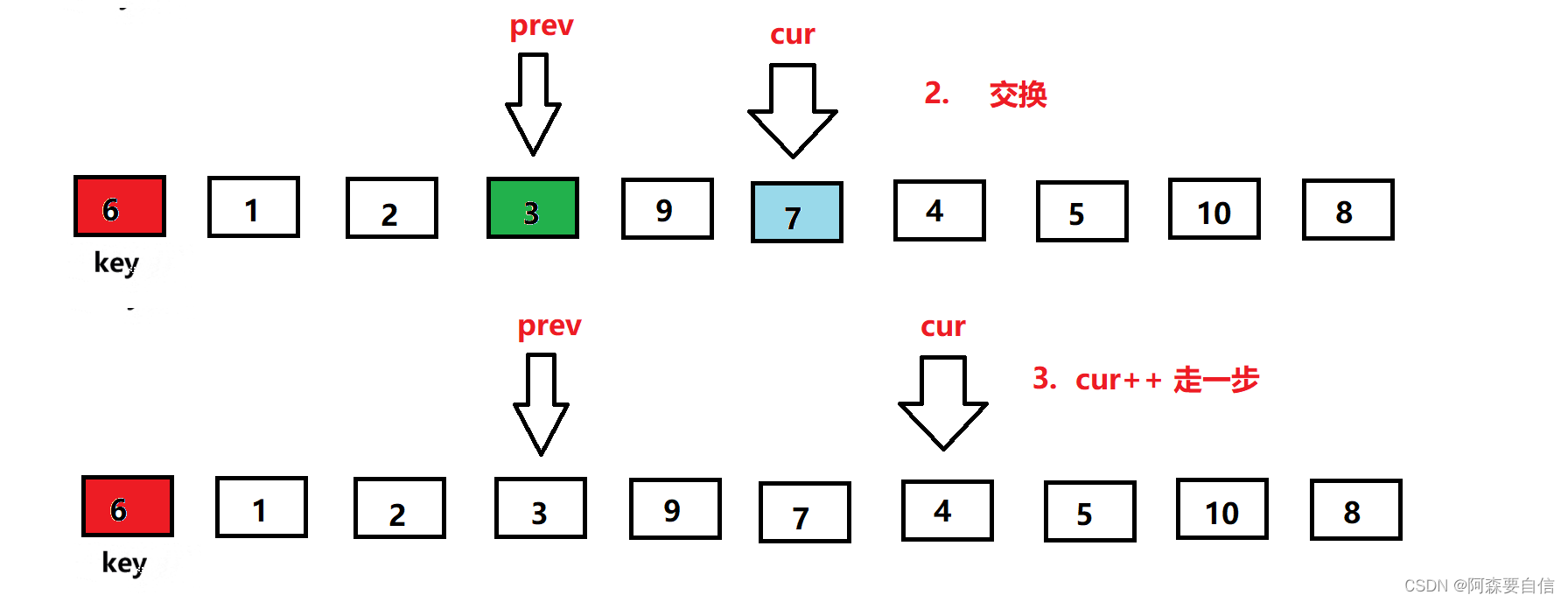
此时此刻,我
cur的值小于key基准值,先让prev走一步,然后与cur的值交换交换
-
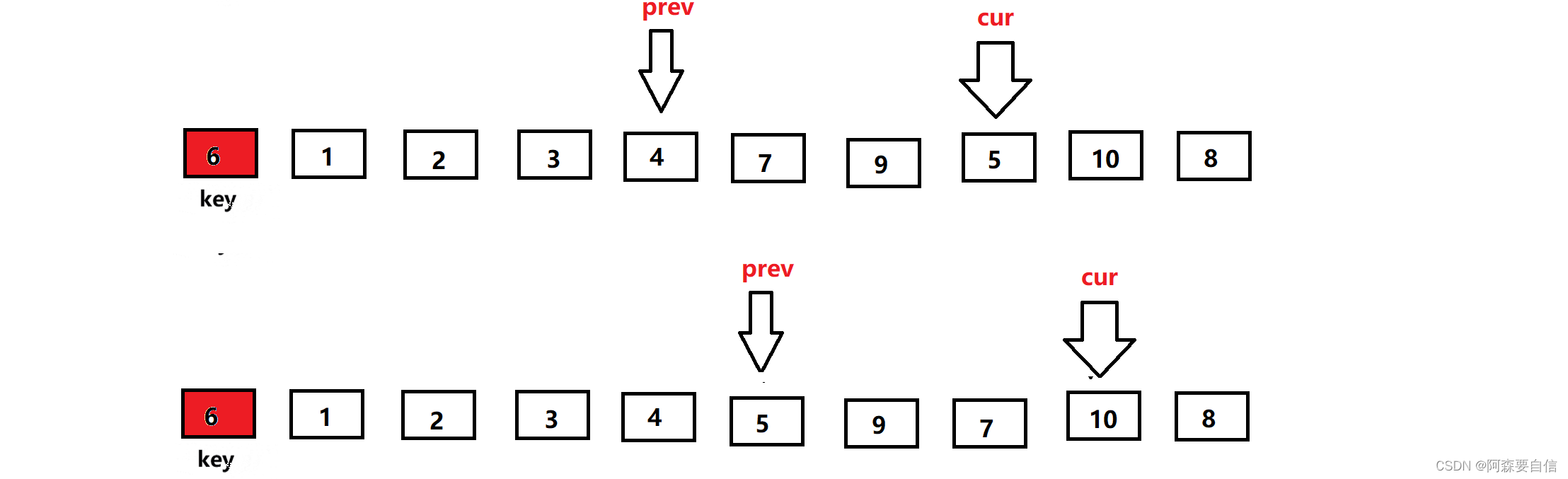
同样的步骤,重复上述遍历,直到遍历完数组

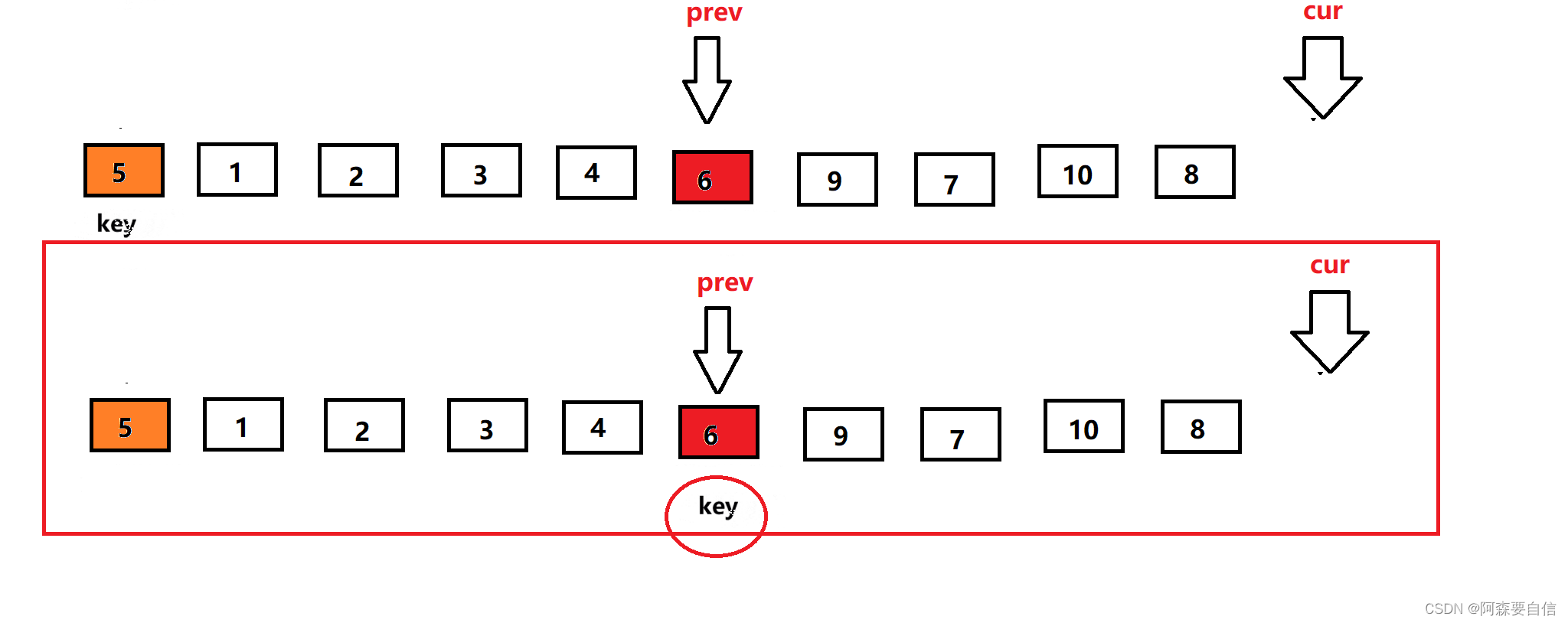
cur遍历完数组后,将交换prev的值key的基准值进行交换,交换完,将key的下标更新为prev下标的,然后返回key下标,完成单趟。
代码如下:
void QuickSort2(int* a, int left, int right)
{// 如果左指针大于等于右指针,表示数组为空或只有一个元素,直接返回if (left >= right)return;// keyi为基准值下标,初始化为左指针int keyi = left;// prev记录每次交换后的下标int prev = left;// cur为遍历指针int cur = left+1;// 循环从左指针+1的位置开始到右指针结束while (cur <= right){// 如果cur位置元素小于基准值,并且prev不等于cur// 就将prev和cur位置元素交换// 并将prev后移一位if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;//不管是cur小于还是大于,是否交换,cur都后移一位 cur都++}// 将基准值和prev位置元素交换Swap(&a[keyi], &a[prev]);// 更新基准值下标为prevkeyi = prev;// 递归调用左右两部分// [left, keyi-1]keyi[keyi+1, right]QuickSort2(a, left, keyi - 1);QuickSort2(a, keyi + 1, right);
}
🌠挖坑法
挖坑法也是快速排序的一种单趟排序方法。它也是利用双指针,但与霍尔法不同的是,挖坑法在每次找到比基准数小的元素时,会将其值填入基准数所在的位置,然后将基准数所在的位置作为“坑”,接着从右边开始找比基准数大的元素填入这个“坑”,如此往复,直到双指针相遇。最后,将基准数填入最后一个“坑”的位置。
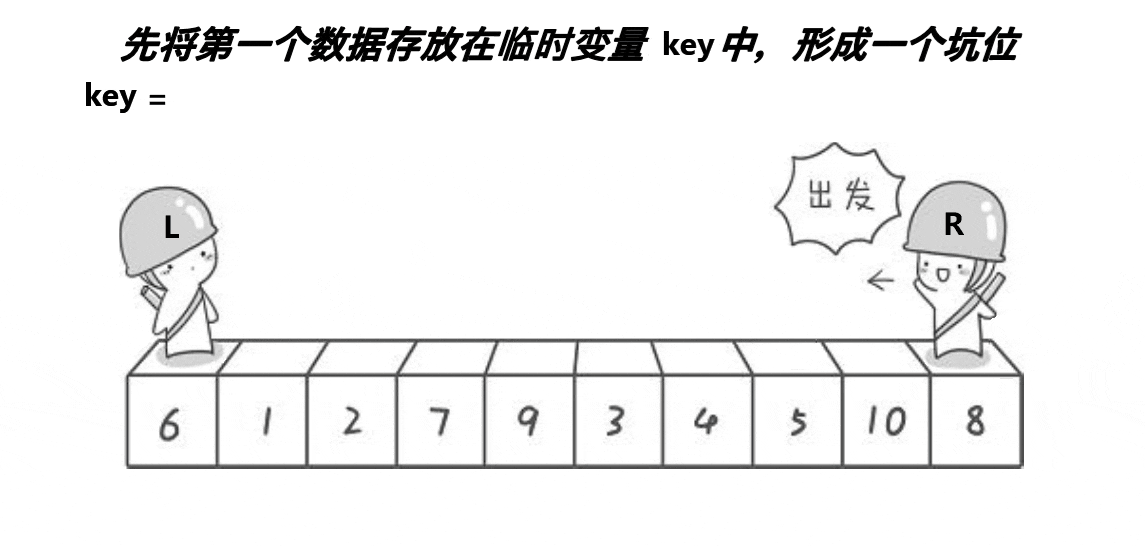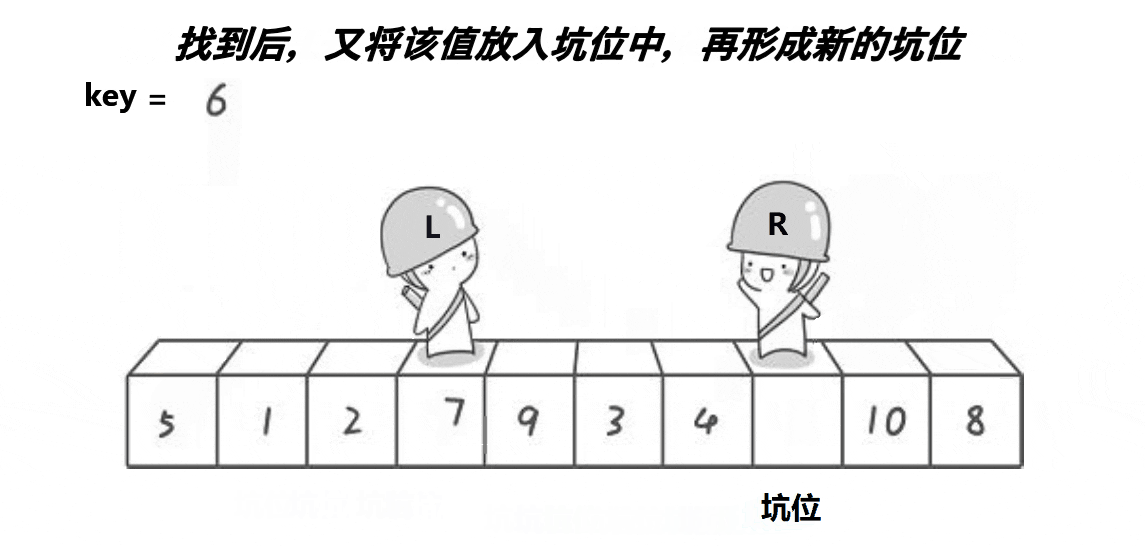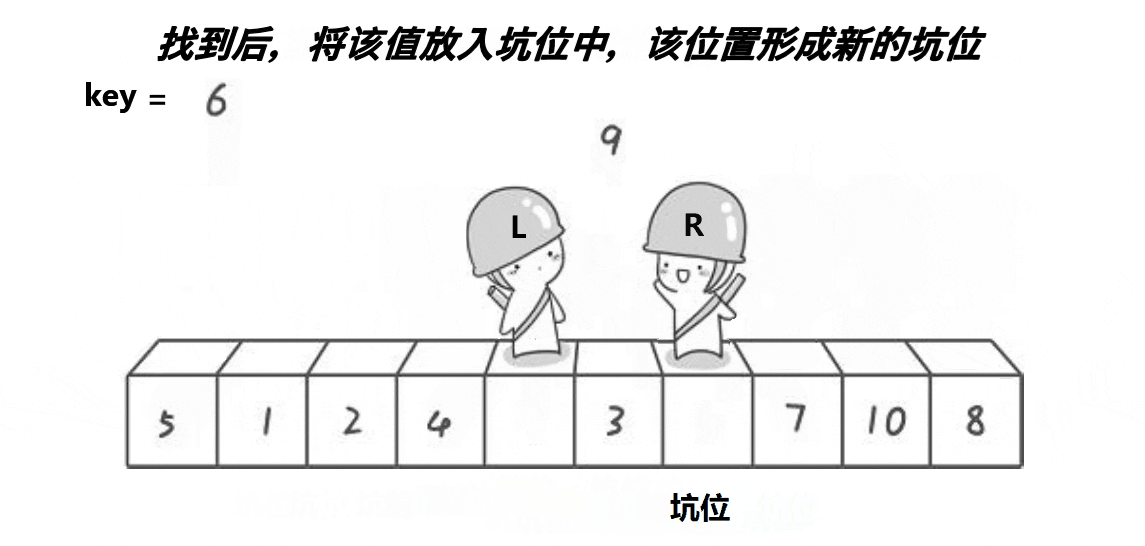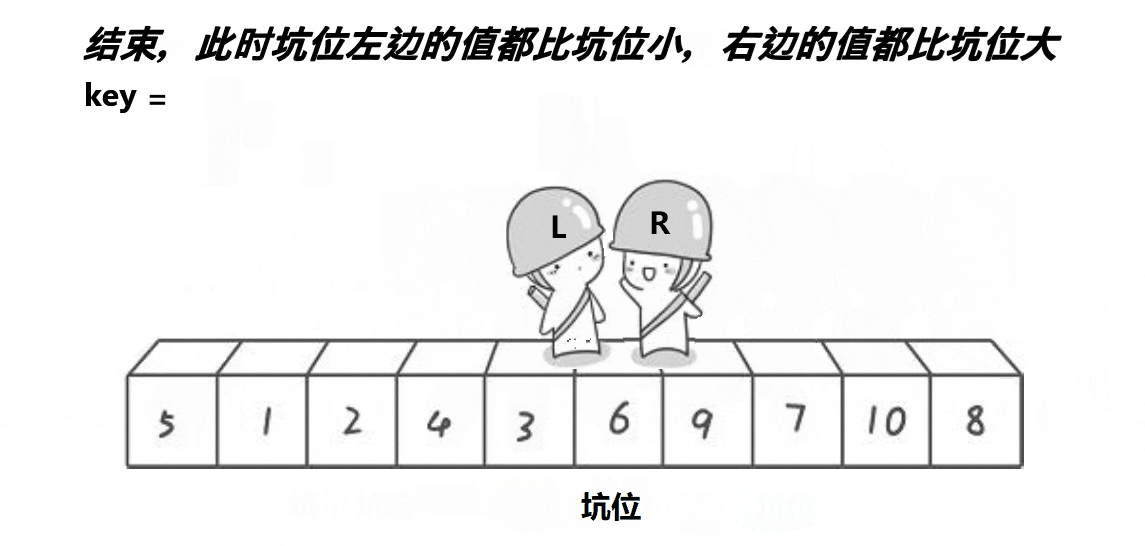
挖坑法思路:
您提到的挖坑法是一种快速排序的实现方式。
- 选择基准值(
key),将其值保存到另一个变量pivot中作为"坑" - 从左往右扫描,找到小于基准值的元素,将其值填入"坑"中,然后"坑"向右移动一个位置
- 从右往左扫描,找到大于或等于基准值的元素,将其值填入移动后的"坑"中
- 重复步骤
2和3,直到左右两个指针相遇 - 将基准值填入最后一个"坑"位置
- 对基准值左右两边递归分治,【
begin,key-1】key【key+1,end】重复上述过程,实现递归排序
与双指针法相比,挖坑法在处理基准值时使用了额外的"坑"变量,简化了元素交换的操作,但思想都是利用基准值将数组分割成两部分。
代码如下:
//挖坑法
void Dig_QuickSort(int* a, int begin, int end)
{if (begin >= end)return;//一趟的实现int key = a[begin];int pivot = begin;int left = begin;int right = end;while (left < right){while (left < right && a[right] >= key){right--;}a[pivot] = a[right];pivot = right;while (left < right && a[left] <= key){left++;}a[pivot] = a[left];pivot = left;}//补坑位a[pivot] = key;//递归分治//[begin, piti - 1] piti [piti + 1, end]Dig_QuickSort(a, begin, pivot - 1);Dig_QuickSort(a, pivot + 1, end);
}
当你讨厌挖左边的坑,可以试试右边的坑😉:
代码如下:
// 交换元素
void swap(int* a, int* b)
{int t = *a;*a = *b;*b = t;
}// 分区操作函数
int partition(int arr[], int low, int high)
{// 取最后一个元素作为基准值int pivot = arr[high];// 初始化左右索引 int i = (low - 1);// 从左到右遍历数组for (int j = low; j <= high - 1; j++) {// 如果当前元素小于或等于基准值if (arr[j] <= pivot) {// 左索引向右移动一位i++;// 将当前元素与左索引位置元素交换 swap(&arr[i], &arr[j]);}}// 将基准值和左索引位置元素交换swap(&arr[i + 1], &arr[high]);// 返回基准值的最终位置return (i + 1);
}// 快速排序主函数
void quickSort(int arr[], int low, int high)
{// 如果低位索引小于高位索引,表示需要继续排序if (low < high) {// 调用分区函数,得到基准值的位置int pi = partition(arr, low, high);// 对基准值左边子数组递归调用快速排序quickSort(arr, low, pi - 1);// 对基准值右边子数组递归调用快速排序 quickSort(arr, pi + 1, high);}
}// 测试
int main()
{// 测试数据int arr1[] = { 5,3,6,2,10,1,4 };int n1 = sizeof(arr1) / sizeof(arr1[0]);quickSort(arr1, 0, n1 - 1);// 输出排序结果for (int i = 0; i < n1; i++){printf("%d ", arr1[i]);}printf("\n");int arr2[] = { 5,3,6,2,10,1,4,29,44,1,3,4,5,6 };int n2 = sizeof(arr2) / sizeof(arr2[0]);quickSort(arr2, 0, n2 - 1);// 输出排序结果for (int i = 0; i < n2; i++){printf("%d ", arr2[i]);}printf("\n");// 测试数据int arr3[] = { 10,1,4,5,3,6,2,1 };int n3 = sizeof(arr3) / sizeof(arr3[0]);quickSort(arr3, 0, n3 - 1);// 输出排序结果for (int i = 0; i < n3; i++){printf("%d ", arr3[i]);}printf("\n");return 0;
}运行启动:

✏️优化快速排序
🌠随机选key
为什么要使用随机数选取
key?
避免最坏情况,即每次选择子数组第一个或最后一个元素作为key,这样会导致时间复杂度退化为O(n^2)。
随机化可以减少排序不均匀数据对算法性能的影响。
相比固定选择第一个或最后一个元素,随机选择key可以在概率上提高算法的平均性能。
这里是优化快速排序使用随机数选取key的方法:
- 在划分子数组前,随机生成一个
[left,right]区间中的随机数randi, - 将随机
randi处的元素与区间起始元素left交换 - 使用这个随机索引取出子数组中的元素作为keyi。
随机选key逻辑代码:
//快排,随机选key
void QuickSort3(int* a, int left, int right)
{//区间只有一个值或者不存在就是最小子问题if (left >= right)return;int begin = left, end = right;//选[left,right]区间中的随机数做keyint randi = rand() % (right - left + 1); //rand() % N生成0到N-1的随机数randi += left; //将随机索引处的元素与区间起始元素交换Swap(&a[left], &a[randi]);//用交换后的元素作为基准值keyiint keyi = left;while (left < right) {//从右向左找小于key的元素while (left < right && a[right] >= a[keyi]) {--right;}//从左向右找大于key的元素 while (left < right && a[left] <= a[keyi]) {++left; }//交换元素Swap(&a[left], &a[right]);}//将基准值与交叉点元素交换Swap(&a[left], &a[keyi]);keyi = left;//递归处理子区间QuickSort3(a, begin, keyi - 1);QuickSort3(a, keyi + 1, end);
}🌉三位数取中
有无序数列数组的首和尾后,我们只需要在首,中,尾这三个数据中,选择一个排在中间的数据作为基准值(keyi),进行快速排序,减少极端情况,进一步提高快速排序的平均性能。
代码实现:
// 三数取中 left mid right
// 大小居中的值,也就是不是最大也不是最小的
int GetMidi(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else // a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}
取中的返回函数接收:
int begin = left, end = right;// 三数取中int midi = GetMidi(a, left, right);//printf("%d\n", midi);Swap(&a[left], &a[midi]);
整体函数实现:
//三数取中 left mid right
//大小居中的值,也就是不是最大,也不是最小的
int GetMid(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if(a[left] > a[right]){return left;}else{return right;}}else//a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if (a[right] > a[left]){return left;}else{return right;}}
}void QuickSort4(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;//三数取中int midi = GetMid(a, left, right);//printf("%d\n",midi);Swap(&a[left], &a[midi]);int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]){--right;}while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;QuickSort4(a, begin, keyi - 1);QuickSort4(a, keyi + 1, end);}
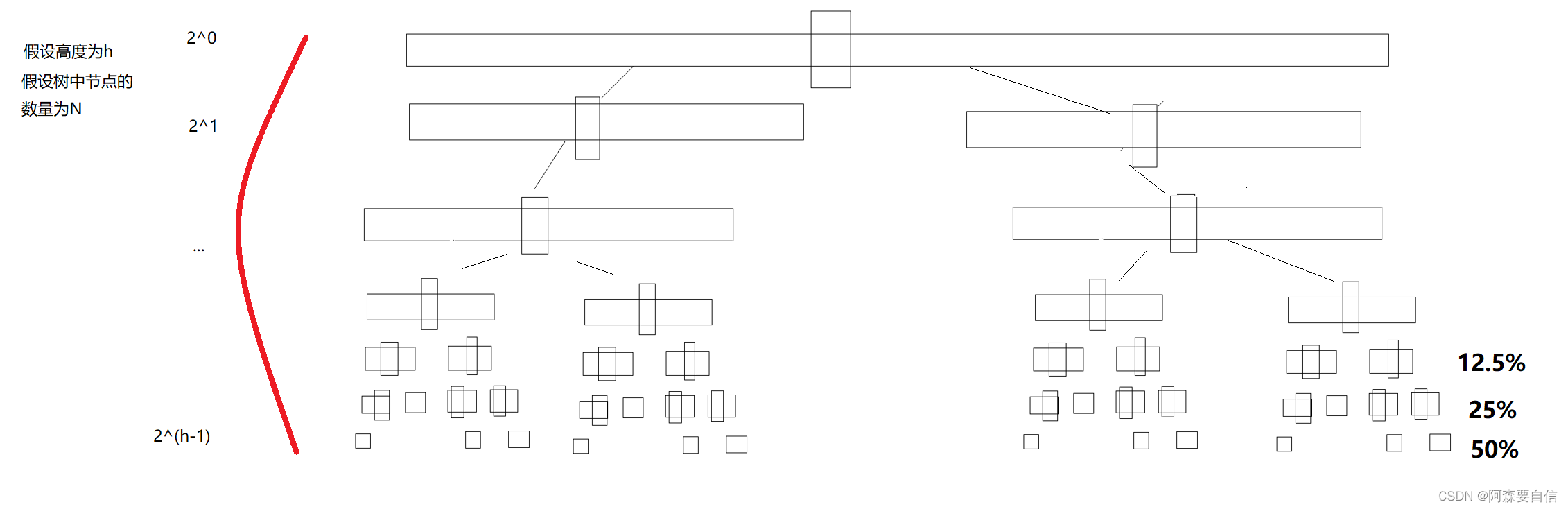
🌠小区间选择走插入,可以减少90%左右的递归
对于小区间,使用插入排序而不是递归进行快速排序。
在快速排序递归中,检查子问题的区间长度是否小于某个阈值(如10-20),如果区间长度小于阈值,则使用插入排序进行排序,否则使用快速排序递归进行划分。
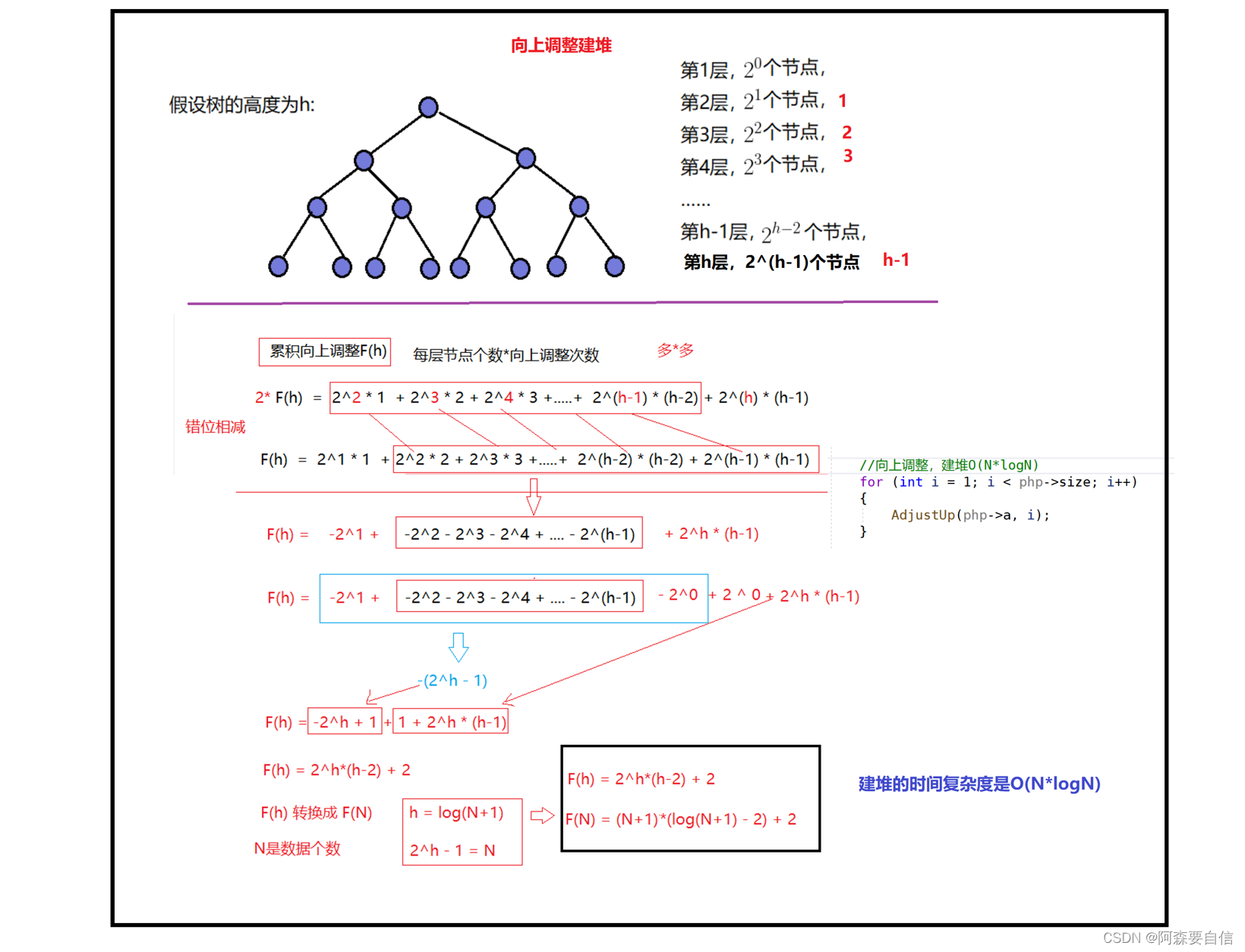
而这个(如10-20)刚好可以在递归二叉树中体现出来。
如图:
当然从向下建堆优于向上建堆,也可以体现出来:
优点在于:对于小区间,插入排序效率高于快速排序的递归开销大部分数组元素位于小区间中,采用插入排序可以省去90%左右的递归调用,但整体数组规模大时,主要工作还是由快速排序完成
与三数取中进行合用
void QuickSort5(int* a, int left, int right)
{if (left >= right)return;// 小区间选择走插入,可以减少90%左右的递归if (right - left + 1 < 10){InsertSort(a + left, right - left + 1);}else{int begin = left, end = right;//三数取中int midi = GetMid(a, left, right);//printf("%d\n",midi);Swap(&a[left], &a[midi]);int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]){--right;}while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;QuickSort4(a, begin, keyi - 1);QuickSort4(a, keyi + 1, end);}
}
🌉 快速排序改非递归版本
逻辑原理:
非递归版本的快速排序利用了栈来模拟递归的过程。它的基本思想是:将待排序数组的起始和结束位置压入栈中,然后不断出栈,进行单趟排序,直到栈为空为止。在单趟排序中,选取基准数,将小于基准数的元素移到基准数左边,大于基准数的元素移到基准数右边,并返回基准数的位置。然后根据基准数的位置,将分区的起始和结束位置入栈,继续下一轮排序,直到所有子数组有序。
代码实现步骤:
- 初始化一个栈用于保存待排序子数组的起始和结束位置。
- 将整个数组的起始和结束位置压入栈中。
- 循环执行以下步骤,直到栈为空:
出栈,获取当前待排序子数组的起始和结束位置。
进行单趟排序,选取基准数,并将小于基准数的元素移到左边,大于基准数的元素移到右边。
根据基准数的位置,将分区的起始和结束位置入栈。 - 排序结束。
代码实现
#include "Stack.h"void QuickSortNonR(int* a, int left, int right)
{ST st;STInit(&st);STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)){int begin = STTop(&st);STPop(&st);int end = STTop(&st);STPop(&st);//单趟int keyi = begin;int prev = begin;int cur = begin + 1;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;//[begin,keyi-1]keyi[keyi+1,end]if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi + 1);}if (keyi - 1 > begin){STPush(&st, keyi - 1);STPush(&st, begin);}}STDestroy(&st);
}
以下是栈的实现:
Stack.c
#include"Stack.h"void STInit(ST* ps)
{assert(ps);ps->a = NULL;ps->top = 0;ps->capacity = 0;
}void STDestroy(ST* ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->top = ps->capacity = 0;
}// 栈顶
// 11:55
void STPush(ST* ps, STDataType x)
{assert(ps);// 满了, 扩容if (ps->top == ps->capacity){int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;STDataType* tmp = (STDataType*)realloc(ps->a, newcapacity * sizeof(STDataType));if (tmp == NULL){perror("realloc fail");return;}ps->a = tmp;ps->capacity = newcapacity;}ps->a[ps->top] = x;ps->top++;
}void STPop(ST* ps)
{assert(ps);assert(!STEmpty(ps));ps->top--;
}STDataType STTop(ST* ps)
{assert(ps);assert(!STEmpty(ps));return ps->a[ps->top - 1];
}int STSize(ST* ps)
{assert(ps);return ps->top;
}bool STEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}
栈的头文件实现:
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>typedef int STDataType;
typedef struct Stack
{STDataType* a;int top;int capacity;
}ST;void STInit(ST* ps);
void STDestroy(ST* ps);// 栈顶
void STPush(ST* ps, STDataType x);
void STPop(ST* ps);
STDataType STTop(ST* ps);
int STSize(ST* ps);
bool STEmpty(ST* ps);
🚩总结
快速排序的特性总结:
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
因此
时间复杂度:O(N*logN)
什么情况快排最坏:有序/接近有序 ->O(N^2)
但是如果加上随机选key或者三数取中选key,最坏情况不会出现,所以这里不看最坏
快排可以很快,你的点赞也可以很快,哈哈哈,感谢💓 💗 💕 💞,喜欢的话可以点个关注,也可以给博主点一个小小的赞😘呀

相关文章:

【排序算法】深入解析快速排序(霍尔法三指针法挖坑法优化随机选key中位数法小区间法非递归版本)
文章目录 📝快速排序🌠霍尔法🌉三指针法🌠挖坑法✏️优化快速排序 🌠随机选key🌉三位数取中 🌠小区间选择走插入,可以减少90%左右的递归🌉 快速排序改非递归版本…...

生成微信小程序二维码
首页 -> 统计 可以通过上面二个地方配置,生成小程序的二维码,并且在推广分析里,有详细的分析数据,...

网络编程(1)写一个简单的UDP网络通信程序【回显服务器】,并且实现一个简单的翻译功能
使用 JAVA 自带的api 目录 一、回显服务器 UdpEchoServer 服务器代码 客户端代码 二、翻译功能 UdpDictServer 在UdpDictServer里重写process方法 一、回显服务器 UdpEchoServer /*** 回显服务器* 写一个简单的UDP的客户端/服务器 通信的程序* 这个程序没有啥业务逻辑&am…...
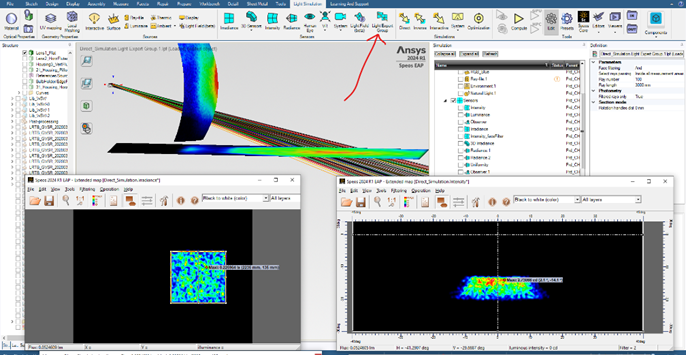
Ansys Speos | Light Expert Group探测器组使用技巧
附件下载 联系工作人员获取附件 概述 相机挡板的设计需要在光路的不同位置同步多个照度图,以尽量减少杂散光。2023R2 Speos提供了一种新的探测器,用于高阶杂散光分析,可以同时对多个探测器进行光线追迹。Light Expert工具可以即时过滤3D视…...
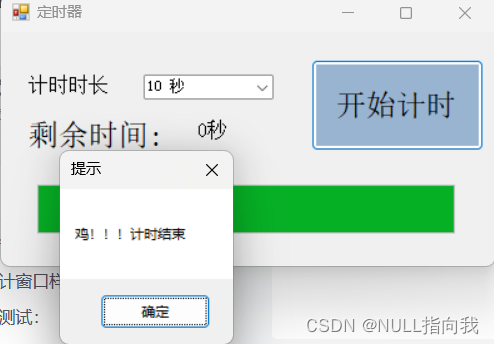
C#学习笔记3:Windows窗口计时器
今日继续我的C#学习之路,今日学习自己制作一个Windows窗口计时器程序: 文章提供源码解释、步骤操作、整体项目工程下载 完成后的效果大致如下:(可选择秒数,有进度条,开始计时按钮等) …...

C语言与sqlite3入门
c语言与sqlite3入门 1 sqlite3数据类型2 sqlite3指令3 sqlite3的sql语法3.1 创建表create3.2 删除表drop3.3 插入数据insert into3.4 查询select from3.5 where子句3.6 修改数据update3.7 删除数据delete3.8 排序Order By3.9 分组GROUP BY3.10 约束 4 c语言执行sqlite34.1 下载…...
——安装Rancher)
Rancher(v2.6.3)——安装Rancher
[详细安装说明请查看Rancher安装说明文档]:https://gitee.com/WilliamWangmy/snail-knowledge/blob/master/Rancher/Rancher%E4%BD%BF%E7%94%A8%E6%96%87%E6%A1%A3.md#1%E5%AE%89%E8%A3%85rancher Rancher部署Mysql(单机版):http…...

Aapche Nutch建立自己的搜索引擎
sudo apt install default-jdk‘ java -version openjdk version "11.0.22" 2024-01-16 vi .bashrc export JAVA_HOME/usr/lib/jvm/java-11-openjdk-amd64 爬梯子下载源代码 Apache Nutch™ – Downloads mkdir -p urls cd urls touch seed.txt 里面放入我的网站…...

阅读笔记(ICIP2023)Rectangular-Output Image Stitching
“矩形输出”图像拼接 Zhou, H., Zhu, Y., Lv, X., Liu, Q., & Zhang, S. (2023, October). Rectangular-Output Image Stitching. In 2023 IEEE International Conference on Image Processing (ICIP) (pp. 2800-2804). IEEE. 0. 摘要 图像拼接的目的是将两幅视场重叠的…...
就业班 第二阶段 2401--3.26 day6 Shell初识 连接vscode
远程连接vs_code可能出现的问题 C:\Users\41703\.ssh 验证远程主机的身份,如果连不上vscode,可以尝试删除这里面的公钥代码。 重新安装那个扩展,排除扩展本身的问题 谁连过我,并操作了什么 curl https://gitea.beyourself.org.c…...

碳课堂|什么是碳资产?企业如何进行碳资产管理?
碳资产是绿色资产的重要类别,在全球气候变化日益严峻的背景下备受关注。在“双碳”目标下,碳资产管理是企业层面实现碳减排目标和低碳转型的关键。 一、什么是碳资产? 碳资产是以碳减排为基础的资产,是企业为了积极应对气候变化&…...

如何使用 ChatGPT 进行编码和编程
文章目录 一、初学者1.1 生成代码片段1.2 解释功能 二、自信的初学者2.1 修复错误2.2 完成部分代码 三、中级水平3.1 研究库3.2 改进旧代码 四、进阶水平4.1 比较示例代码4.2 编程语言之间的翻译 五、专业人士5.1 模拟 Linux 终端 总结 大多数程序员都知道,ChatGPT …...

学习java第二十四天
spring框架中有哪些不同类型的事件 Spring 提供了以下5种标准的事件: 上下文更新事件(ContextRefreshedEvent):在调用 ConfigurableApplicationContext 接口中的refresh方法时被触发。 上下文开始事件(ContextStart…...

中小型集群部署,Docker Swarm(集群)使用及部署应用介绍
1、Docker Swarm简介 说到集群,第一个想到的就是k8s,但docker官方也提供了集群和编排解决方案,它允许你将多个 Docker 主机连接在一起,形成一个“群集”(Swarm),并可以在这个 Swarm 上运行和管…...

gateway做负载均衡
在Spring Cloud中,Gateway可以通过配置文件来实现负载均衡。以下是一个简单的配置示例,它演示了如何将请求代理到名为service-instance的服务的两个不同实例。 spring:cloud:gateway:routes:- id: service-instance-routeuri: lb://service-instancepre…...
)
pytorch中的torch.hub.load()
pytorch提供了torch.hub.load()函数加载模型,该方法可以从网上直接下载模型或是从本地加载模型。官方文档 torch.hub.load(repo_or_dir, model, *args, sourcegithub, trust_repoNone, force_reloadFalse, verboseTrue, skip_validationFalse, **kwargs)参数说明&a…...
R语言学习——Rstudio软件
R语言免费但有点难上手,是数据挖掘的入门级别语言,拥有顶级的可视化功能。 优点: 1统计分析(可以实现各种分析方法)和计算(有很多函数) 2强大的绘图功能 3扩展包多,适合领域多 …...

触发器的工艺结构原理及选型参数总结
🏡《总目录》 目录 1,概述2,工作原理3,结构特点4,工艺流程4.1,掩膜制作4.2,晶片生长4.3,晶片切割4.4,晶片清洗4.5,掩膜光刻4.6,金属沉积5,选型参数5.1,触发类型5.2,触发频率...
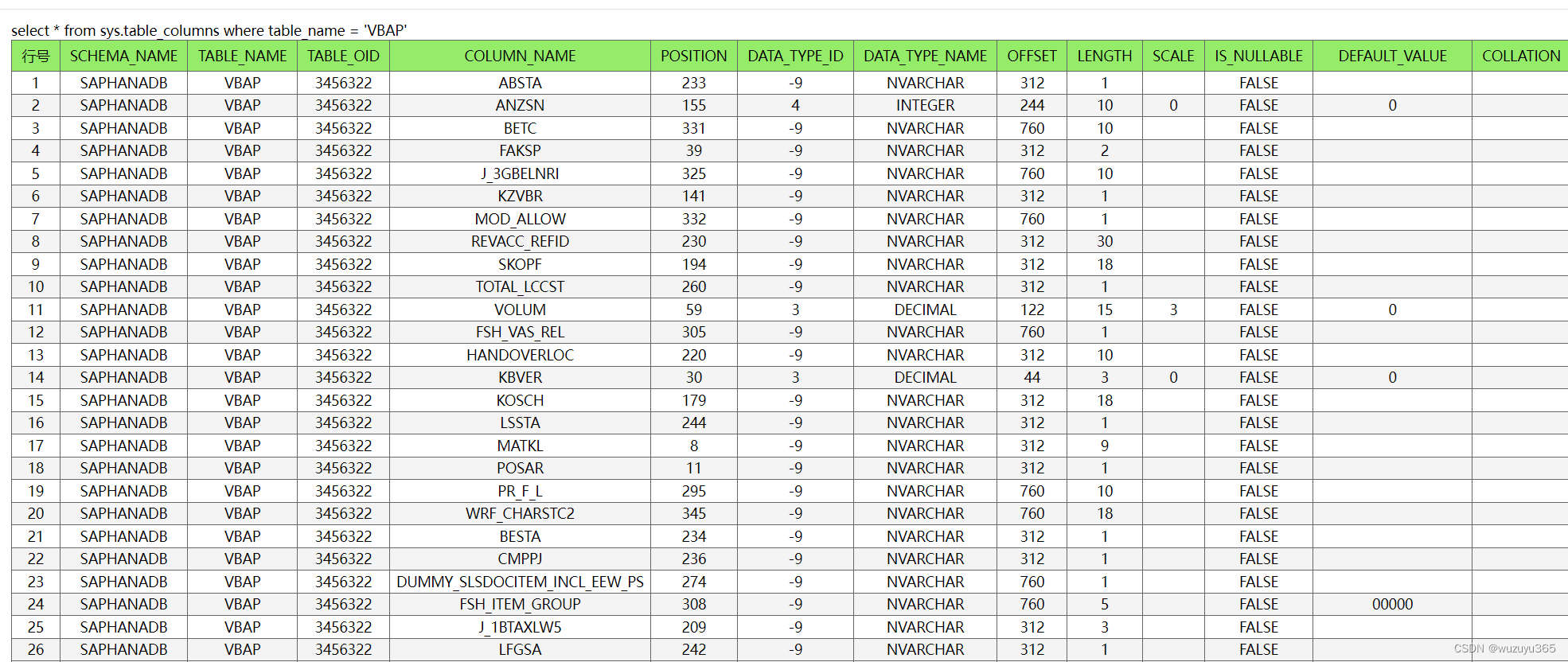
Hana数据库 No columns were bound prior to calling SQLFetch or SQLFetchScroll
在php调用hana数据库的一个sql时报错了,查表结构的sql: select * from sys.table_columns where table_name VBAP SQLSTATE[SL009]: <<Unknown error>>: 0 [unixODBC][Driver Manager]No columns were bound prior to calling SQLFetch …...

DevOps是什么
DevOps 是一种将软件开发 (Dev) 和 IT运维 (Ops) 结合起来的实践、文化和哲学,旨在缩短系统开发生命周期,提供高质量的软件持续交付。它涉及多个关键实践和工具,其核心目的是加强开发和运维团队之间的协作和通信。以下是构成DevOps的一些重要…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...