PTA天梯赛习题 L2-006 树的遍历
先序遍历:根-左-右 => 序列的第一个数就是根
中序遍历:左-根-右 => 知道中间某一个数为根,则这个数的左边就是左子树,右边则是右子树
后序遍历:左-右-根 => 序列的最后一个数就是根
题目
给定一棵二叉树的后序遍历和中序遍历,请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。
输入格式:
输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。
输出格式:
在一行中输出该树的层序遍历的序列。数字间以1个空格分隔,行首尾不得有多余空格。
输入样例:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
输出样例:
4 1 6 3 5 7 2题解
思路都在代码里面,因为这个题的数据范围比较小,才这样做的,大家可以看注释,写的比较清楚
如有问题,欢迎指正
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N= 1e5 + 24, inf = 1e9 + 7, M = 1e1+24;
int post[M], in[M];
int position[N]; //记录中序遍历的每个点的下标位置
vector<int> a(N, -1); //用来装中序遍历的结果(待筛选)
vector<int> ans; //最后的结果
// 解释一下参数含义:
/*
root:根在后序遍历中的位置,从n开始
head-tail:中序遍历的范围是从1-n开始的
idx:层次遍历的下表, 用a[idx] 来记录的,
但是a不是最终的结果,因为这不是一棵完全二叉树,我把a都置为-1了,只有非-1才是我们的结果,后面会处理的,先不管
*/
void build(int root, int head, int tail, int idx)
{if(tail < head) return; //到叶子了,回溯a[idx] = post[root] ; //先把根记录下来//找到根在中序遍历的位置,index之前的数就是左子树,之后的数就是右子树 // 一共有(tail-head+1)个数,前面有(index-head)个数,后面有(tail-index)个数 int index = position[post[root]] ;/*下面这一部分可能不是很好理解,大家可以在纸上画一下*/ //左子树 /*左子树的root隔了右子树的个数+1这么多个数,+的那个1是root范围就是:head~index-1 */build(root-(tail-index+1), head, index-1, idx*2);//开始右子树/*右子树的根的位置在root-1 中序遍历的范围锁定(index的右边):index+1 ~ tail中序遍历根的序号为idx*2+1 */ build(root-1, index+1, tail, idx*2+1);
}
int main()
{int n, i, j , k;
// memset(a, -1, sizeof(a));cin >> n;// 二叉树的后序遍历for(i = 1; i <= n; i ++){cin >> post[i];}// 二叉树的中序遍历for(i = 1; i <= n; i ++){cin >> in[i];//position用来 记录各个值在中序遍历中的位置,后面会用到 // 这里假设键值都是互不相等的正整数,依据这个条件,如果有重的元素就不行了哈 position[in[i]] = i;}//build里面的参数含义见上方函数定义 build(n, 1, n, 1); for(i = 0; i < a.size(); i ++){if(a[i] != -1){ans.push_back(a[i]);} }for(i = 0; i < ans.size(); i ++){if(i > 0) cout << " ";cout << ans[i];}return 0;
}相关文章:

PTA天梯赛习题 L2-006 树的遍历
先序遍历:根-左-右 > 序列的第一个数就是根 中序遍历:左-根-右 > 知道中间某一个数为根,则这个数的左边就是左子树,右边则是右子树 后序遍历:左-右-根 > 序列的最后一个数就是根 题目 给定一棵…...

js相关的dom方法
查找元素 //获取元素id为box的元素 document.getElementById(box) //获取元素类名为box的元素 document.getElementsByClassName(box) //获取标签名为div的元素 document.getElementsByTagName(div)改变元素 //设置id为box的元素内容 document.getElementById("box"…...

Django——Ajax请求
Django——Ajax请求 一、响应 Json 数据 path(str/ , views.str_view), path(json/ , views.json_view), path(jsonresponse/ , views.jsonresponse_view), path(ls/ , views.ls),from django.shortcuts import render , HttpResponse from django.http import JsonResponse …...
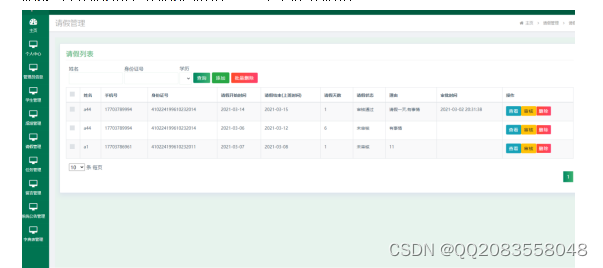
基于java多角色学生管理系统论文
摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本学生管理系统就是在这样的大环境下诞生,其可以帮助管理者在短时间内处理完毕庞大的数据信息&am…...
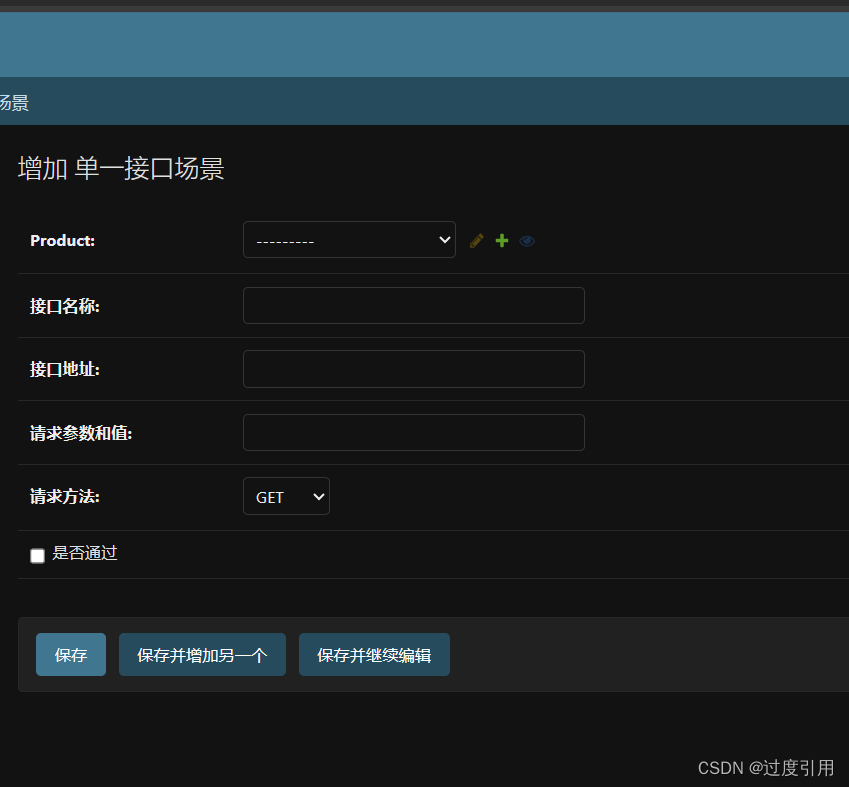
python(django)之单一接口管理功能后台开发
1、创建数据模型 在apitest/models.py下加入以下代码 class Apis(models.Model):Product models.ForeignKey(product.Product, on_deletemodels.CASCADE, nullTrue)# 关联产品IDapiname models.CharField(接口名称, max_length100)apiurl models.CharField(接口地址, max_…...

教程1_图像视频入门
一、图像入门 1、cv2.imread()函数 cv2.imread() 是 OpenCV 库中的一个函数,用于读取图像文件。下面是 cv2.imread() 函数的基本介绍和使用方法: 函数定义 cv2.imread(filename, flagscv2.IMREAD_COLOR) 参数 filename:要读取的图像的路…...
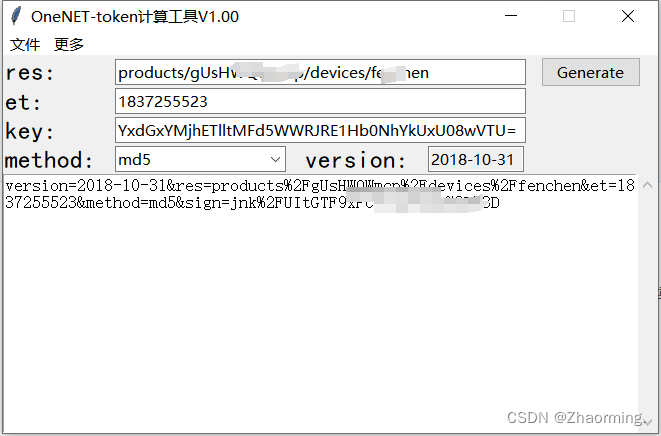
MQTT.fx和MQTTX 链接ONENET物联网提示账户或者密码错误
参考MQTT.fx和MQTTX 链接ONENET物联网开发平台避坑细节干货。_mqttx和mqttfx-CSDN博客 在输入password和username后还是提示错误,是因为在使用token的时候,key填写错误,将设备的密钥填入key中...

Svn添加用户、添加用户组、配置项目权限等自动化配置脚本
实现在工作中自动化配置svn用户、用户组、和项目权限的脚本,在使用过程中如果有什么问题,可以联系我。 移步到gitee: svn account permission management: Svn账号、组、权限管理脚本 (gitee.com)...
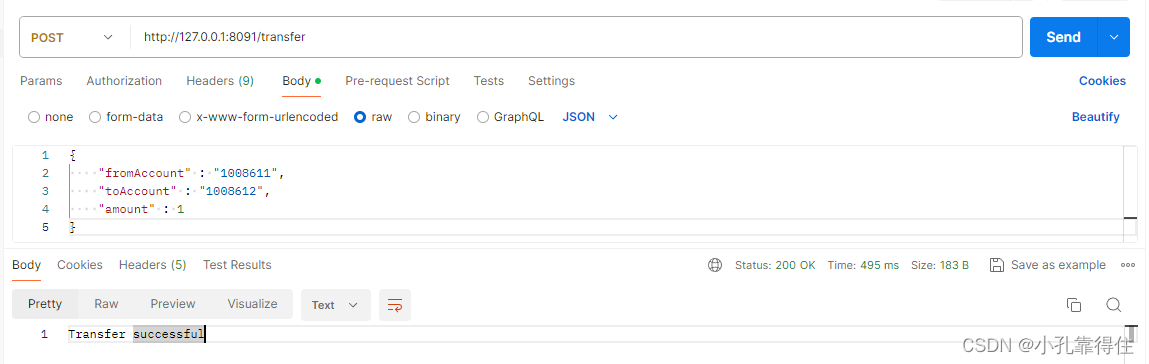
Spring事务-两种开启事务管理的方式:基于注解的声明式事务管理、基于编程式的事务管理
Spring事务-两种开启事务管理的方式 1、前期准备2、基于注解的声明式事务管理3、基于编程式的事务管理4、声明式事务失效的情况 例子:假设有一个银行转账的业务,其中涉及到从一个账户转钱到另一个账户。在这个业务中,我们需要保证要么两个账户…...

OC 技术 苹果内购
一直觉得自己写的不是技术,而是情怀,一个个的教程是自己这一路走来的痕迹。靠专业技能的成功是最具可复制性的,希望我的这条路能让你们少走弯路,希望我能帮你们抹去知识的蒙尘,希望我能帮你们理清知识的脉络࿰…...

云原生周刊:Kubernetes v1.30 一瞥 | 2024.3.25
开源项目推荐 Retina Retina 是一个与云无关的开源 Kubernetes 网络可观测平台,它提供了一个用于监控应用程序运行状况、网络运行状况和安全性的集中中心。它为集群网络管理员、集群安全管理员和 DevOps 工程师提供可操作的见解,帮助他们了解 DevOps、…...

2016年认证杯SPSSPRO杯数学建模D题(第一阶段)NBA是否有必要设立四分线解题全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 D题 NBA是否有必要设立四分线 原题再现 NBA 联盟从 1946 年成立到今天,一路上经历过无数次规则上的变迁。有顺应民意、皆大欢喜的,比如 1973 年在技术统计中增加了抢断和盖帽数据;有应运而生、力挽狂澜的&am…...
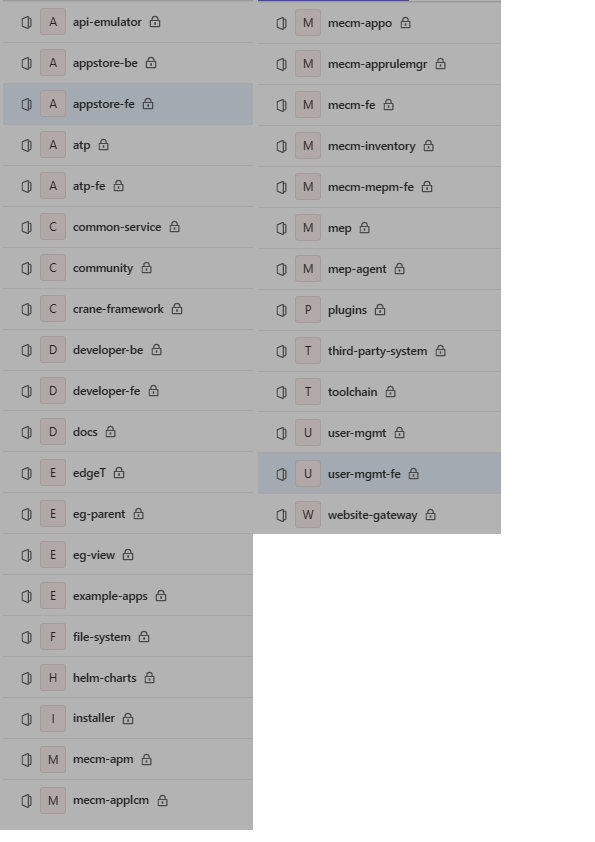
EdgeGallery开发指南
API接口 简介 EdgeGallery支持第三方业务系统通过北向接口网关调用EdgeGallery的业务接口。调用流程如下图所示(融合前端edgegallery-fe包含融合前端界面以及北向接口网关功能,通过浏览器访问时打开的是融合前端的界面,通过IP:Port/urlPref…...
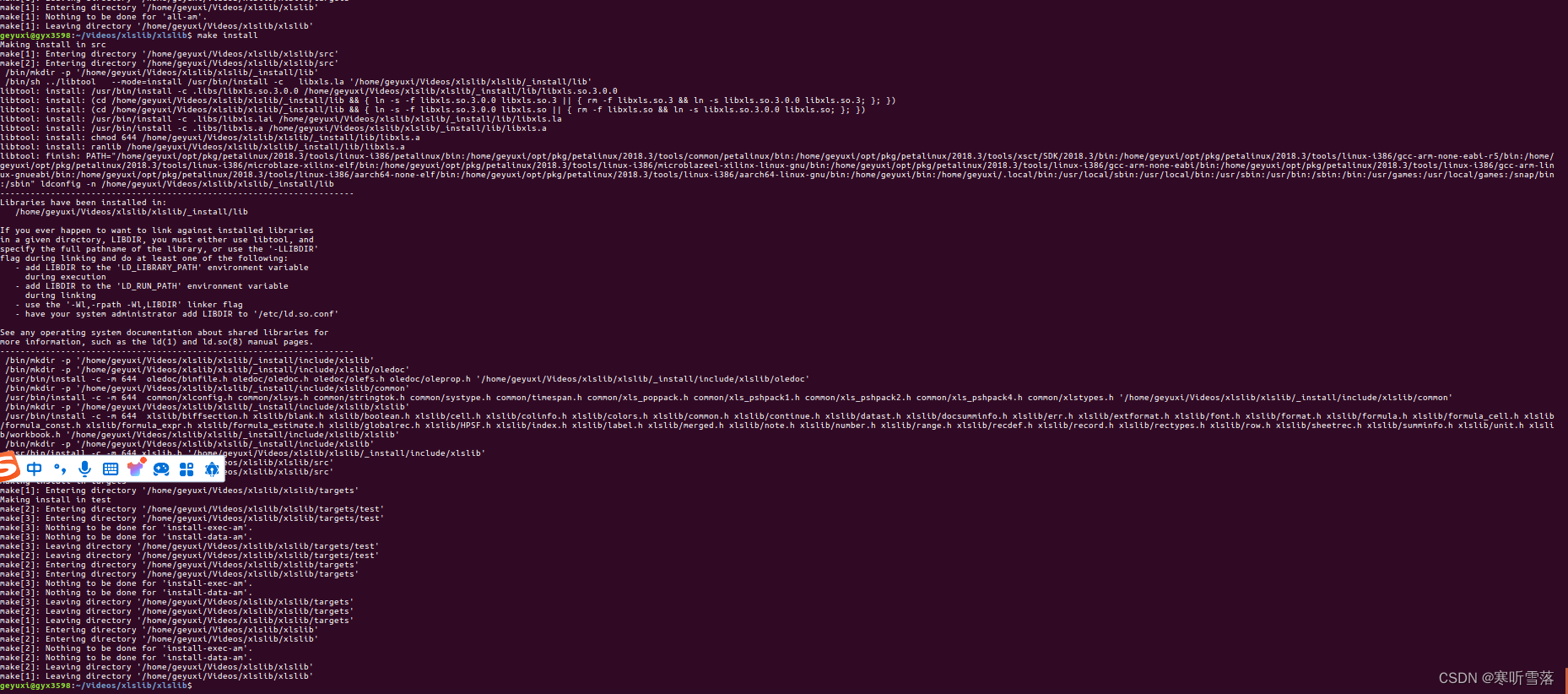
ubuntu arm qt 读取execl xls表格数据
一,ubuntu linux pc编译读取xls的库 1,安装libxls(读取xls文件 电脑版) 确保你已经安装了基本的编译工具,如gcc和make。如果没有安装,可以使用以下命令安装: sudo apt-update sudo apt-get install build-essentia…...
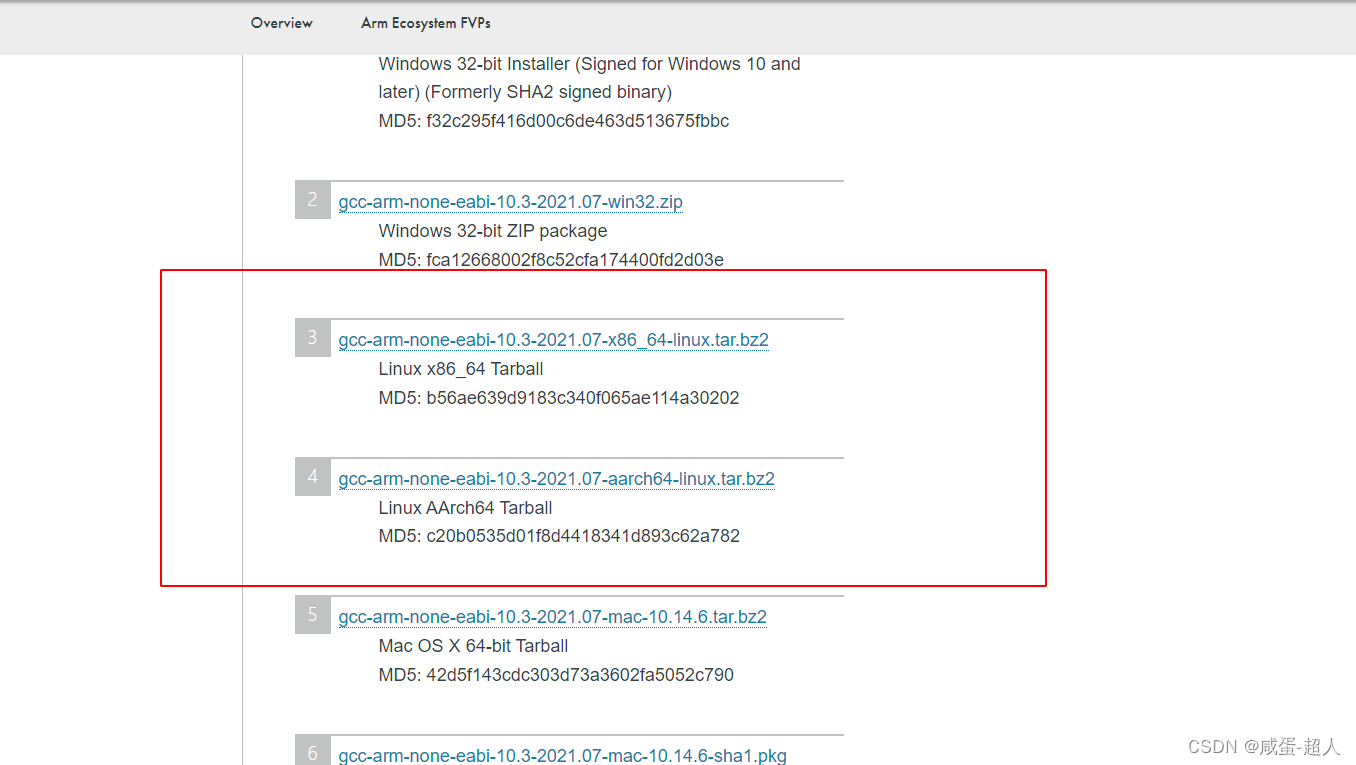
STM32 使用gcc编译介绍
文章目录 前言1. keil5下的默认编译工具链用的是哪个2. Arm编译工具链和GCC编译工具链有什么区别吗?3. Gcc交叉编译工具链的命名规范4. 怎么下载gcc-arm编译工具链参考资料 前言 我们在STM32上进行开发时,一般都是基于Keil5进行编译下载,Kei…...

FPGA之组合逻辑与时序逻辑
数字逻辑电路根据逻辑功能的不同,可以分成两大类:组合逻辑电路和时序逻辑电路,这两种电路结构是FPGA编程常用到的,掌握这两种电路结构是学习FPGA的基本要求。 1.组合逻辑电路 组合逻辑电路概念:任意时刻的输出仅仅取决…...
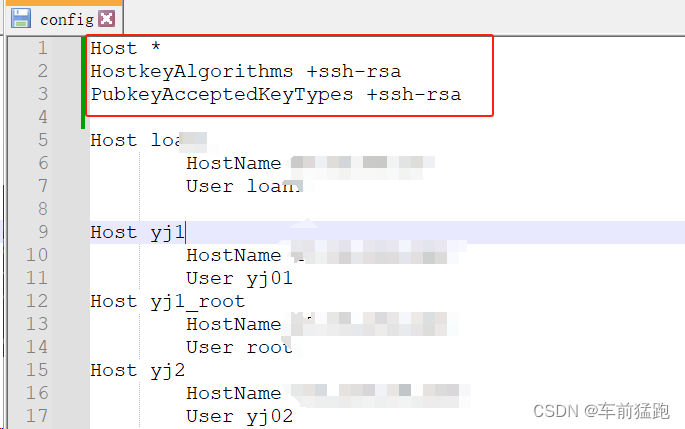
git clone没有权限的解决方法
一般情况 git clone时没有权限,一般是因为在代码库平台上没有配置本地电脑的id_rsa.pub 只要配置上,一般就可以正常下载了。 非一般情况 但是也有即使配置了id_rsa.pub后,仍然无法clone代码的情况。如下 原因 这种情况是因为ssh客户端…...

Redis 的内存回收策略
Redis的内存回收策略用于处理过期数据和内存溢出情况,确保系统稳定性和性能。作为一个高性能的键值存储系统,它通过内存回收策略来维护内存的高效使用 主要包括过期删除策略和内存淘汰策略。 过期删除策略: Redis的过期删除策略是通过设置…...
小程序富文本图片宽度自适应
解决这个问题 创建一个util.js文件,图片的最大宽度设置为100%就行了 function formatRichText(html) {let newContent html.replace(/\<img/gi, <img style"max-width:100%;height:auto;display:block;");return newContent; }module.exports {formatRichT…...

安装redis时候修改过的配置文件
只要是石头,到哪里都不会发光的 bind 绑定主机某个网卡对应的IP地址,如果某个主机有两个网卡A和B,那么绑定了A,通过B连接就会无法访问protected-mode 保护模式 Yes为只能本地访问port 启动的端口号pidfile pid存放的位置ÿ…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
