浙大版《C语言程序设计(第4版)》题目集-习题3-5 三角形判断
给定平面上任意三个点的坐标(x1,y1)、(x2,y2)、(x3,y3),检验它们能否构成三角形。
输入格式:
输入在一行中顺序给出六个[−100,100]范围内的数字,即三个点的坐标x1、y1、x2、y2、x3、y3。
输出格式:
若这3个点不能构成三角形,则在一行中输出“Impossible”;若可以,则在一行中输出该三角形的周长和面积,格式为“L = 周长, A = 面积”,输出到小数点后2位。
输入样例1:
4 5 6 9 7 8
输出样例1:
L = 10.13, A = 3.00
输入样例2:
4 6 8 12 12 18
输出样例2:
Impossible
法一:海伦公式
-
判断是否为三角形: 根据任意两边之和大于第三边
-
求三角形面积:海伦公式。设三角形三边分别为a,b,c,三角形的面积则为: S = p ( p − a ) ( p − b ) ( p − c ) ) S=\sqrt{ p(p-a)(p-b)(p-c) )} S=p(p−a)(p−b)(p−c)) ,其中p=(a+b+c)/2; a,b,c为三角形的各边。
#include <stdio.h>
#include <math.h>int main(){double x1, y1, x2, y2, x3, y3;double edge1, edge2, edge3, L, A;scanf("%lf %lf %lf %lf %lf %lf", &x1, &y1, &x2, &y2, &x3, &y3);// 计算三条边长度edge1 = sqrt( pow(x1-x2, 2) + pow(y1-y2, 2) );edge2 = sqrt( pow(x1-x3, 2) + pow(y1-y3, 2) );edge3 = sqrt( pow(x2-x3, 2) + pow(y2-y3, 2) );// 判断是否为三角形: 根据任意两边之和大于第三边if( edge1+edge2>edge3 && edge1+edge3>edge2&& edge2+edge3>edge1 ){L = edge1 + edge2 + edge3;double p= L / 2;A = sqrt(p * (p - edge1) * (p - edge2) * (p - edge3));printf("L = %.2lf, A = %.2lf", L, A);}elseprintf("Impossible");return 0;
}
法二:二阶行列式的几何意义,但是运行错误,没找到错在哪儿
#include <stdio.h>
#include <math.h>int main() {float x1, y1, x2, y2, x3, y3;float edge1, edge2, edge3, L, A;scanf("%f %f %f %f %f %f", &x1, &y1, &x2, &y2, &x3, &y3);edge1 = sqrt(pow(x1 - x2, 2) + pow(y1 - y2, 2));edge2 = sqrt(pow(x1 - x3, 2) + pow(y1 - y3, 2));edge3 = sqrt(pow(x2 - x3, 2) + pow(y2 - y3, 2));L = edge1 + edge2 + edge3;float x20,y20,x30,y30;x20 =x2- x1;y20 = y2-y1;x30 = x3-x1;y30 = y3-y1;A=fabs((x20*y30-y20*x30)/2.0);// 判断是否为三角形:根据任意两边之和大于第三边if (A>0.00000001) {printf("L = %.2f, A = %.2f", L, A);} elseprintf("Impossible");return 0;
}
运行结果

易错点:
- 忘记fabs:abs() 会对浮点数取整,对浮点数取绝对值,要用fabs
- scanf: GPT说某些编译器可能对scanf()函数的 %lf 格式支持不佳,导致读取实数值时出现问题,为了确保正确的实数值输入,可以将%lf改为%f。(错误原因是输入位实数,和浮点数有关,是否是scanf(“%lf”)导致的错误,还未确认。
相关文章:

浙大版《C语言程序设计(第4版)》题目集-习题3-5 三角形判断
给定平面上任意三个点的坐标(x1,y1)、(x2,y2)、(x3,y3),检验它们能否构成三角形。 输入格式: 输入在一行中顺序给出六个[−100,100]范围内的数字,即三个点的坐标x1、y1、x2、y2、x3、y3。 输出格式: 若这3个点不能构成三角形,则在一行中输…...

Java封装、继承、多态和抽象深度解析
在软件工程的世界里,面向对象编程(OOP)是一种编程范式,它使用“对象”来设计软件。对象可以封装数据和方法,以提高代码的复用性、可维护性和可扩展性。Java作为一门面向对象的编程语言,提供了四个基本的面向…...
深度学习每周学习总结P3(天气识别)
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 | 接辅导、项目定制 数据链接 提取码:o3ix 目录 0. 总结1. 数据导入部分数据导入部分代码详解:a. 数据读取部分a.1 提问:关…...

通过iOS网络抓包工具实现移动应用数据安全监控
摘要 本文将深入探讨iOS平台上常用的网络抓包工具,包括Charles、克魔助手、Thor和Http Catcher,以及通过SSH连接进行抓包的方法。此外,还介绍了克魔开发助手作为iOS应用开发的辅助工具,提供的全方面性能监控和调试功能。 在iOS应…...

Stable Diffusion WebUI 生成参数:脚本(Script)——提示词矩阵、从文本框或文件载入提示词、X/Y/Z图表
本文收录于《AI绘画从入门到精通》专栏,专栏总目录:点这里,订阅后可阅读专栏内所有文章。 大家好,我是水滴~~ 在本篇文章中,我们将深入探讨 Stable Diffusion WebUI 的另一个引人注目的生成参数——脚本(Script)。我们将逐一细说提示词矩阵、从文本框或文件导入提示词,…...

synchronized和volatile的原理及应用
文章目录 synchronized的实现原理及应用升级锁代码示例volatile原理及应用代码示例线程不安全类 synchronized的实现原理及应用 synchronized 是Java中用于实现线程同步的关键字,可以应用于方法或代码块,确保在多线程环境下对共享资源的安全访问。下面是…...

Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单实战案例 之九 简单闪烁效果
Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单实战案例 之九 简单闪烁效果 目录 Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单实战案例 之九 简单闪烁效果 一、简单介绍 二、简单闪烁效果实现原理 三、简单闪烁效果案例实现简单步骤 四、注意事项 一、简单…...

11 开源鸿蒙OpenHarmony轻量系统源码分析
开源鸿蒙轻量系统源码分析 作者将狼才鲸日期2024-03-28 一、前言 之前单独的LiteOS是通过Makefile编译的,当前的开源鸿蒙LiteOS-M和LiteOS-A是通过gn和ninja编译的。 Gitee官方只介绍了LiteOS-M的gn ninja编译的流程,针对M3使用Keil编译的流程可能要参…...
专题:一个自制代码生成器(嵌入式脚本语言)之应用实例
初级代码游戏的专栏介绍与文章目录-CSDN博客 我的github:codetoys,所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。 这些代码大部分以Linux为目标但部分代码是纯C的,可以在任何平台上使用。 专题:一个自制代码…...
Appium设备交互API
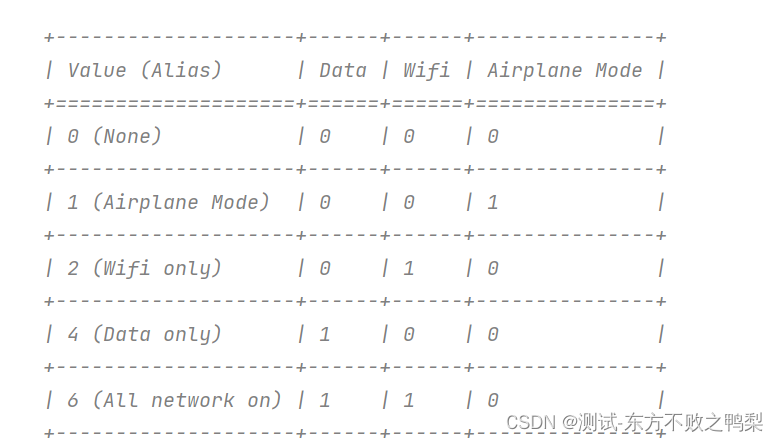
设备交互API指的是操作设备系统中的一些固有功能,而非被测程序的功能,例如模拟来电,模拟发送短信,设置网络,切换横竖屏,APP操作,打开通知栏,录屏等。 模拟来电 make_gsm_call(phon…...

Qlib-Server部署
Qlib-Server部署 介绍 构建Qlib服务器,用户可以选择: 一键部署Qlib服务器逐步部署Qlib服务器一键部署 Qlib服务器支持一键部署,用户可以选择以下两种方法之一进行一键部署: 使用docker-compose部署在Azure中部署使用docker-compose进行一键部署 按照以下步骤使用docker…...

CMC学习系列 (4):β段CMC可以作为一种中风治疗的生物标志物和治疗靶点
CMC学习系列:β段CMC可以作为一种中风治疗的生物标志物和治疗靶点 0. 引言1. 主要贡献2. 方法2.1 相干源动态成像2.2 源统计分析 3. 结果3.1 训练前后比较3.2 源代码分析3.3 皮质重叠的分组分析 4. 讨论5. 总结欢迎来稿 论文地址:https://www.sciencedirect.com/sci…...
jmeter中参数加密
加密接口常用的方式有: MD5,SHA,HmacSHA RSA AES,DES,Base64 压测中有些参数需要进行加密,加密方式已接口文档为主。 MD5加密 比如MD5加密的接口文档: 请求URL:http://101.34.221…...

YOLOv8改进 | 检测头篇 | 2024最新HyCTAS模型提出SAttention(自研轻量化检测头 -> 适用分割、Pose、目标检测)
一、本文介绍 本文给大家带来的改进机制是由全新SOTA分割模型(Real-Time Image Segmentation via Hybrid Convolutional-TransformerArchitecture Search)HyCTAS提出的一种SelfAttention注意力机制,论文中叫该机制应用于检测头当中(论文中的分割效果展现目前是最好的)。我…...
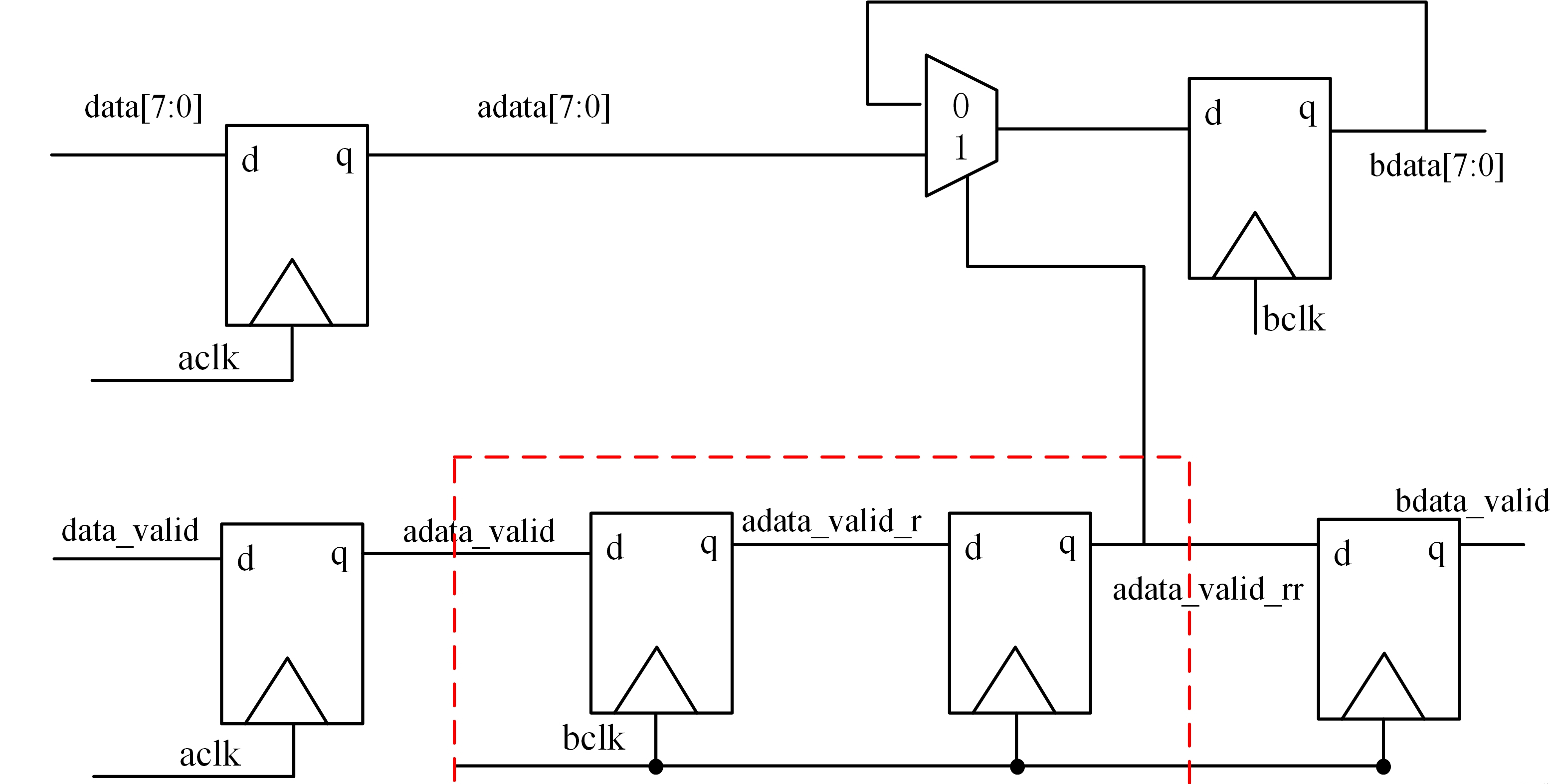
verilog设计-cdc:多比特信号跨时钟域(DMUX)
一、前言 多比特一般为数据,其在跨时钟域传输的过程中有多种处理方式,比如DMUX,异步FIFO,双口RAM,握手处理。本文介绍通过DMUX的方式传输多比特信号。 二、DMUX同步跨时钟域数据 dmux表示数据分配器,该方…...
服务器停止解析域名,但仍然可以访问到
1.centos7 如何刷新dns缓存 在CentOS 7上,DNS缓存由nscd(Name Service Cache Daemon)管理,如果系统上安装了nscd,可以通过清除nscd缓存来刷新DNS缓存。 要刷新DNS缓存,请执行以下命令: sudo …...

Centos系统与Ubuntu系统防火墙区别,以及firewalld、ufw和iptables三者之前的区别。
现在大多数Centos系统上的防火墙是firewalld,Ubuntu系统上是ufw,而iptables是最底层的防火墙工具。iptables是Linux系统中最早的防火墙工具,并且被许多不同的Linux发行版使用,包括CentOS和Ubuntu。然而,CentOS 7及更高…...

ES6 学习(三)-- es特性
文章目录 1. Symbol1.1 使用Symbol 作为对象属性名1.2 使用Symbol 作为常量 2. Iterator 迭代器2.1 for...of循环2.2 原生默认具备Interator 接口的对象2.3 给对象添加Iterator 迭代器2.4 ... 解构赋值 3. Set 结构3.1 初识 Set3.2 Set 实例属性和方法3.3 遍历3.4 相关面试题 4…...

使用ChatGPT的场景之gpt写研究报告,如何ChatGPT写研究报告
推荐写研究报告使用智能站: dayfire.cn/ 1. 确定研究主题 明确主题:在开始之前,你需要有一个清晰的研究主题。这将帮助AI更好地理解你的需求…...
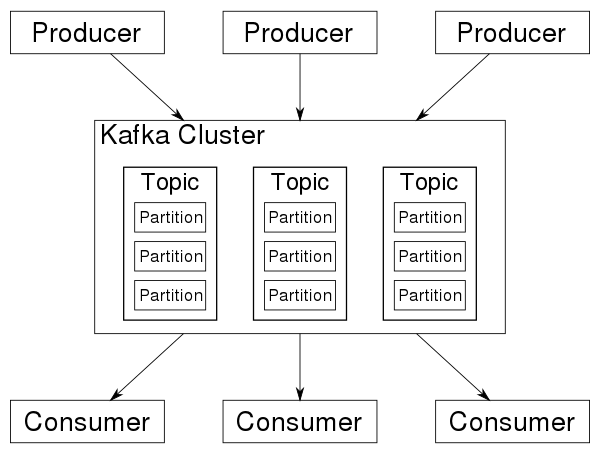
librdkafka的简单使用
文章目录 摘要kafka是什么安装环境librdkafka的简单使用生产者消费者 摘要 本文是Getting Started with Apache Kafka and C/C的中文版, kafka的hello world程序。 本文完整代码见仓库,这里只列出producer/consumer的代码 kafka是什么 本节来源&#…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...

VSCode 使用CMake 构建 Qt 5 窗口程序
首先,目录结构如下图: 运行效果: cmake -B build cmake --build build 运行: windeployqt.exe F:\testQt5\build\Debug\app.exe main.cpp #include "mainwindow.h"#include <QAppli...
