bsd猜想 Murmuration of Eliptic Curves(笔记)
- BSD Alexey Pozdnyakov (University of Connecticut) YUTUBE视频, B站搬运地址
- 新生代女数学家Nina Zubrilina得到椭圆曲线椋鸟群飞模式精确公式与证明
Arithmetic Geometry算术几何
希尔伯特第十问题
-
希尔伯特第十问题(Hilbert’s Tenth Problem)是由德国数学家大卫·希尔伯特在1900年提出的一系列23个数学问题中的第十个问题。这个问题涉及到对于多项式方程是否存在一种通用的算法,用于判断方程是否有整数解。具体来说,希尔伯特问的是:
是否存在一个算法,能够确定一个给定的整系数多项式方程是否有整数解。 -
这个问题直到1970年才在苏联数学家尤里·马脱维奇·马特亚塔斯耶维奇·达尼洛维奇 (Yuri Matiyasevich) 的工作下得到回答。他证明了类似于戴尔宾斯(Julia Robinson)、马丁-戴维斯(Martin Davis)和普特南(Hilary Putnam)的一般形式的数学逻辑理论是适用于证明
这样的算法不存在的。 -
但是简单情况是有办法的。

-
我们只需要考虑一些更简单的问题和一种方法来做到这一点是限制多项式,我们看到限制它们的明显方法是查看变量较少且次数较低的多项式。
-
因此如果我们一直到单变量多项式,这个问题实际上就变成了有理根定理。允许我们确定该多项式是否有有理根
2-Variable Quadratics
- 如果我们有一个带有整数系数的二阶二变量多项式,

- 有两种情况, 要么没有有理解,要么有无限多个, 我们使用仓促的明可夫斯基定理来确定这一点,然后我们实际上可以明确地找到第二种情况下的所有解决方案呃
- 您只需找到一个有理解调用那个 p 然后你采取,通过 p 的所有有理斜率线并计算这些线与圆锥曲线的第二个交点,这实际上会给你所有有理点,这实际上会给你所有有理点
- 当然, 收集它们的线将具有合理的斜率,因为 x 和 a 会有合理的变化。
- y 的有理变化 um 反过来有点复杂,但本质上如果你有一条线穿过有理点以计算第二个交点。你把这条线插入二次曲线, 或者你把它代入, 嗯,这给你的是一个二阶一变量多项式,它具有所有有理系数, 并且你知道的根之一是有理数,因为它去有理点, 所以当然二阶也必须是理性的,嗯, 是的, 这基本上就是所有两个变量的情况
- 有点尴尬, 这是我们可以采取的最高情况。一旦你尝试处理更复杂的情况,哈西·明可夫斯基定理就会失败。
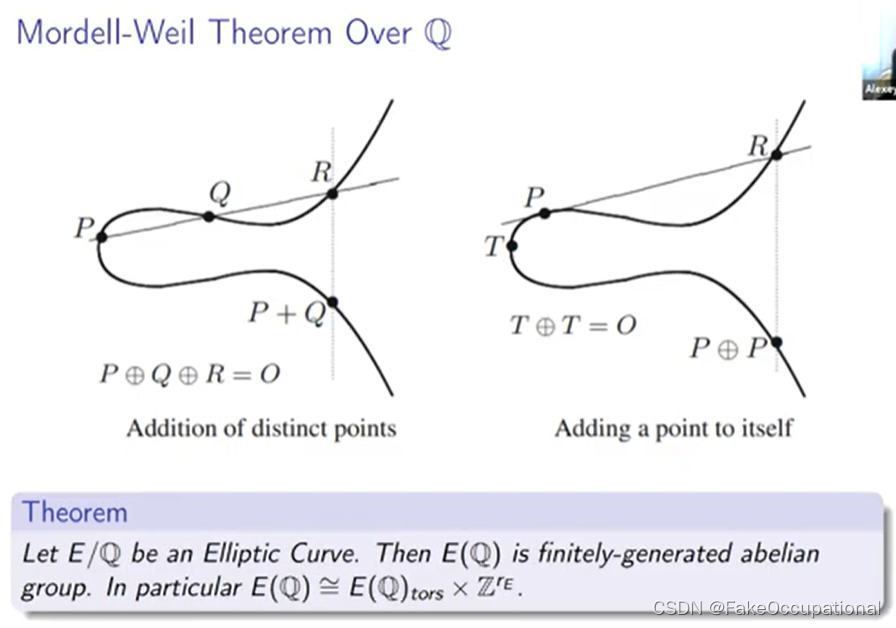
Mordell-Weil Theorem Over Q
椭圆曲线
- 所以如果你采用三次方程 3 x 立方加 4 y 立方加 5,就会有一个非常著名的反例z 那么这只有平凡的有理数解。
- 我们无法真正完全解决这些更困难的方程,所以这就是椭圆曲线出现的地方
- 椭圆曲线是属一的平滑射影代数曲线,平滑意味着没有尖点或扭结,或者导数永远不会同时消失射影意味着我们将在射影平面上工作
- 所以这个抽象定义与我们一直在研究的方程有一个定理,它说域 k 上的每个椭圆曲线 e 都同构于由以下方程给出的曲线, 正如您所看到的, 它是一个二变量三阶方程关于这个同构的另一件事是它总是可以将指定的点 o 发送为无穷远点
是的, 也许更令人惊讶的是这个定理的逆,所以每条光滑的三次曲线都同构于椭圆曲线- 系数的多项式条件, 因此椭圆曲线构成了所有可能的三次曲线的扎斯基开子集,当然这意味着它们在所有三次曲线的集合中是密集的。

- 所以这个定理基本上告诉我们如何在给定一些已知的有理点的情况下生成新的有理点,如果你有两个有理点 p 和 q 你可以画一个穿过这些点的线然后该线将在呃第三个点处与立方体相交,事实证明, 这一点总是有理数。
Simple Open Problems

Understanding Rank - BSD Conjecture
- 所以如果你让 e 超过 fp 成为一条椭圆曲线有限域,你可以定义这个特定的量 ap , ap 是 p 加一减去 fp 上该曲线上的点数
- 所以当你查看椭圆曲线 mod p 和 um 时,你有多少个解, 这个量本质上是一个错误对解数量的某种估计,独立于等级, 你可以计算出你期望有多少个解,

Strong form BSD Conjecture The L-function of an elliptic curve is defined to be
椭圆曲线的L函数
- 这是这些非常好的方程之一,它将一个非常分析的对象与一个非常代数的对象联系起来

ML探索

Logistic Regression

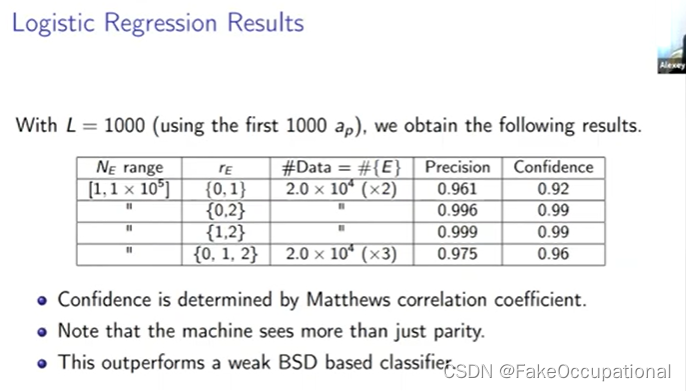
Logistic Regression Results
-
逻辑回归所做的事情与简单地近似不同,逻辑回归具有区分排名第一和排名第二的最佳性能,因此使用 bsd 公式排序,排名越远, 差异就越大。
-
但逻辑回归实际上表现最好区分排名一和排名二,逻辑回归是一种相当可解释的机器学习方法,只需查看该权重向量即可了解模型的 ap 依赖性。
-
特别是我们可以绘制权重向量的分量,并尝试了解它如何对不同 ap 进行加权,当我们这样做时, 我们会得到排名 0 与排名 1 的图模型。
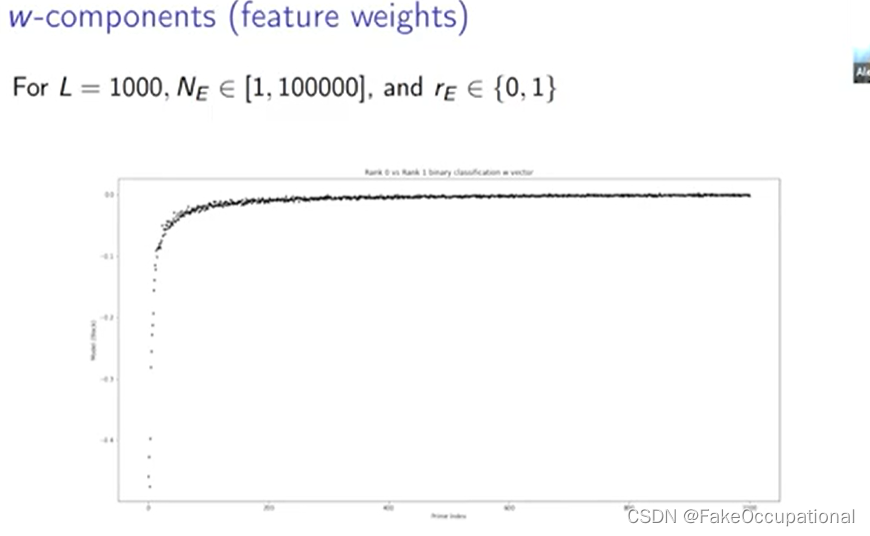
- 这里的所有或大部分权重都是负数,所以这意味着我们对 ap 进行负权重,这种情况是由 bsd 猜想解释的,
Principle Component Analysis (PCA)
- 我们还想尝试一种无监督学习方法,我们只需将其交给 ap 并让它对数据进行某种分析,我们所做的就是主成分分析 (PCA) 或主成分分析 (principal)。

PCA Result
- 这些是对排名 0、1 和 2 的每个排名的 12 000 条曲线进行采样的结果,似乎第一个主成分实际上是在排名上的,所以这告诉我们, ap 数据集中最大的方差实际上是由排名决定的
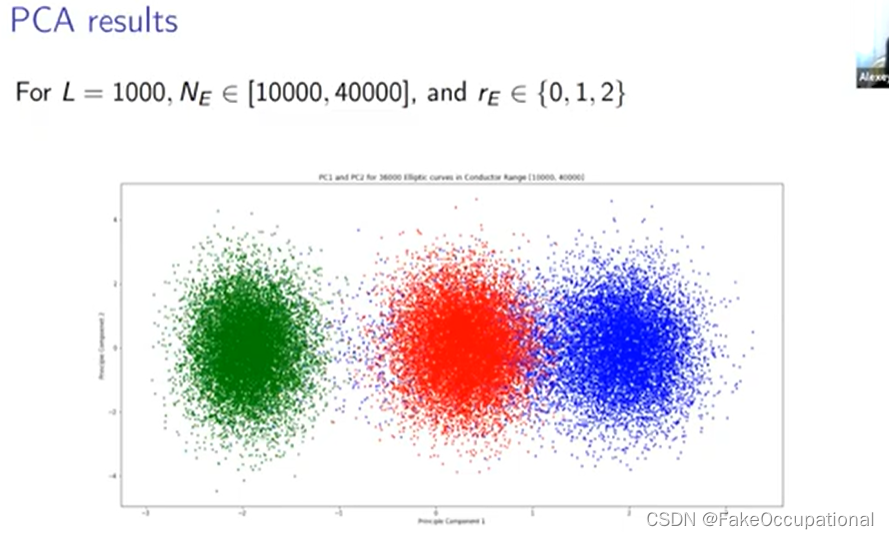
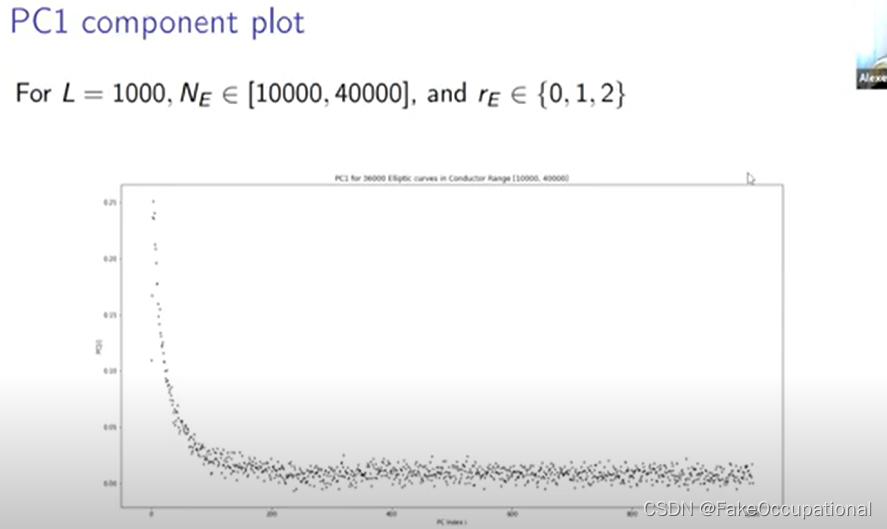
- 最后的 PCA 结果有点没有最好的分离,特别是在排名零和排名一之间
- 嗯, 我们感兴趣的一件事是尝试在两者之间获得更好的分离,因此我们能够通过首先删除所有排名二的点来做到这一点,
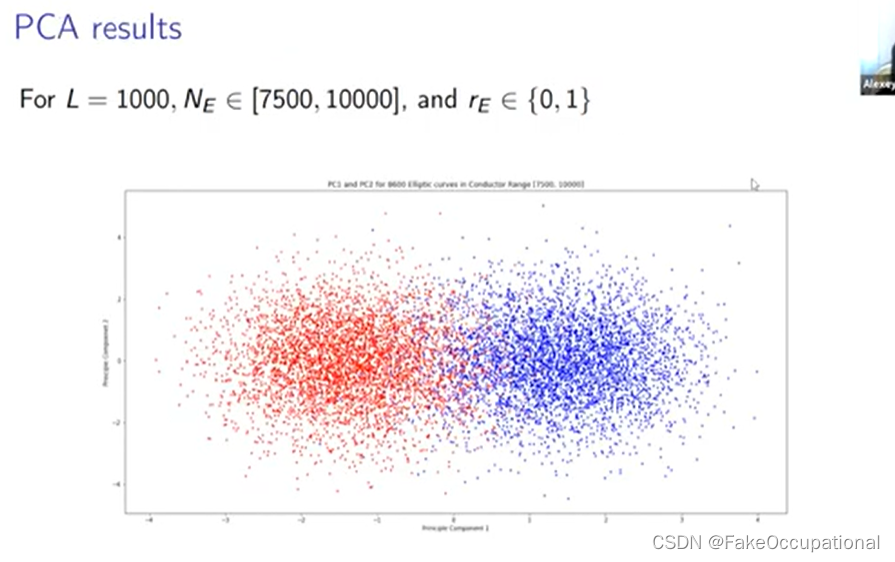
PC1 component plot
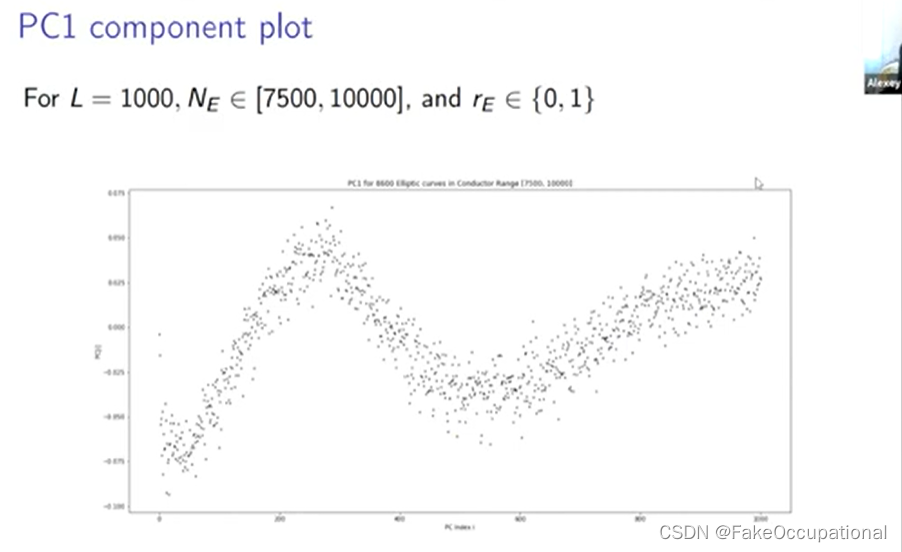
- 它不再是正值或负值,它在两者之间来回振荡,然后它从负值开始变得正也不再是前一百个 ap 中的大部分权重,正如您所看到的, 权重有点遵循这种平滑的振荡
- 这个主成分图的作用是告诉我们当我们将这些 ap 投影到低维子空间时我们采用什么 ap 的线性组合,在这个高维空间中, 平均等级零平均等级一曲线是什么样子
- 那么我们如何才能看看这条平均曲线,我们需要定义我们要平均的椭圆曲线集,所以我们在这里使用 n1 到 m2 的 er 来实现这一点,它只是秩等于 r 的所有椭圆曲线的集合
- 然后我们在这里定义这个函数,因此 n 的 fr 只是这整组椭圆曲线上的第 n 个 ap 的平均值,

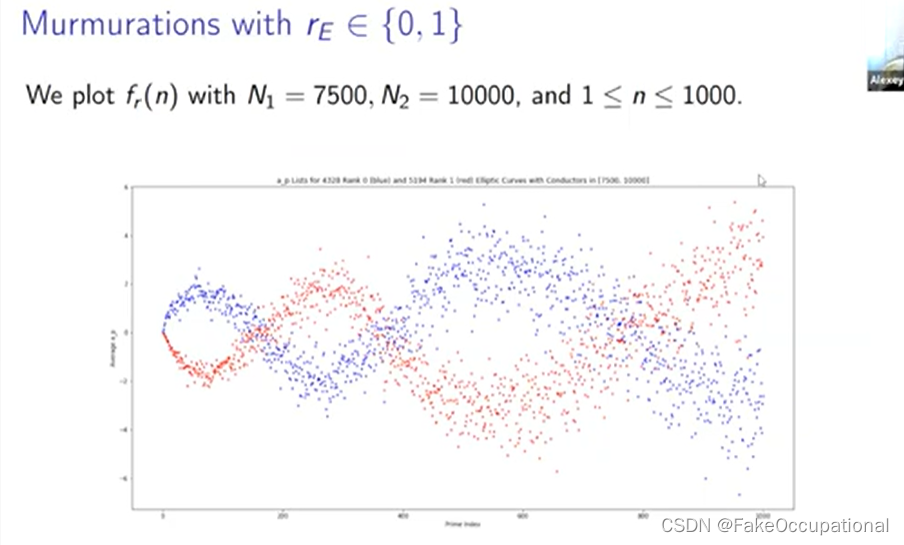
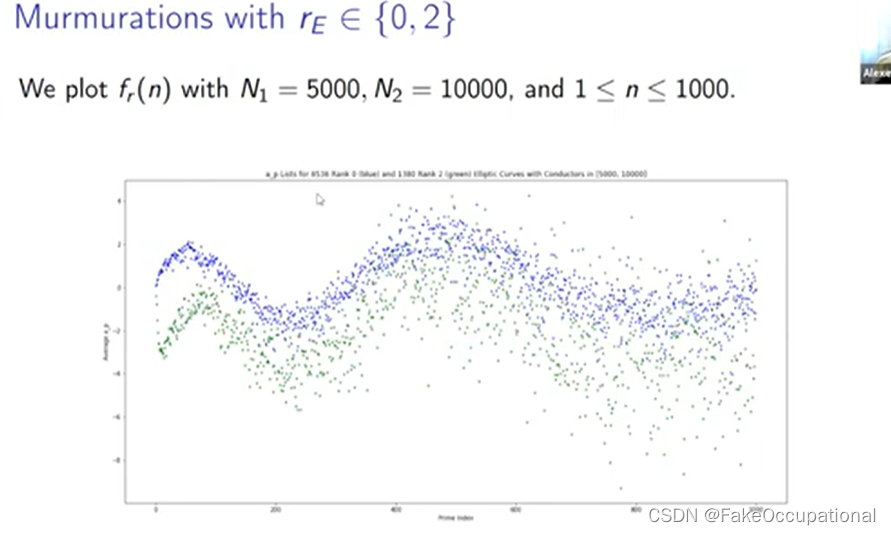
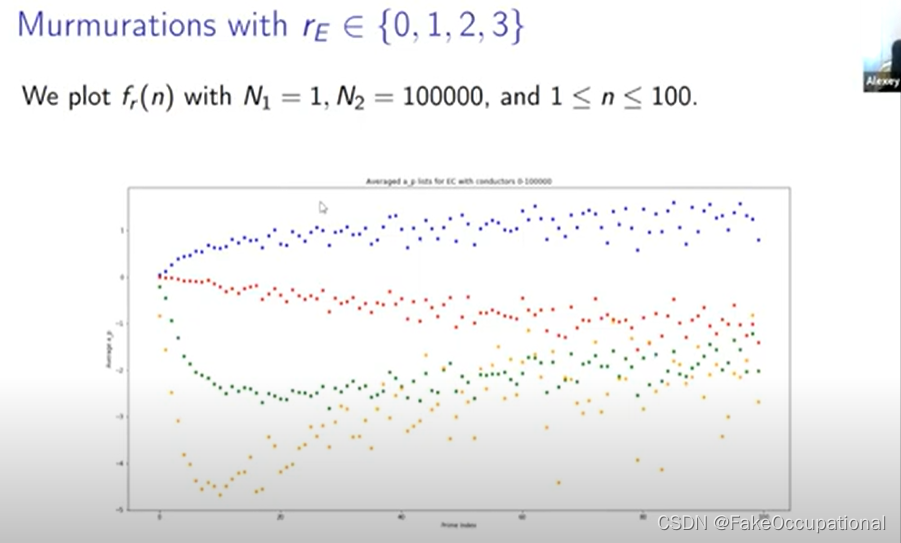
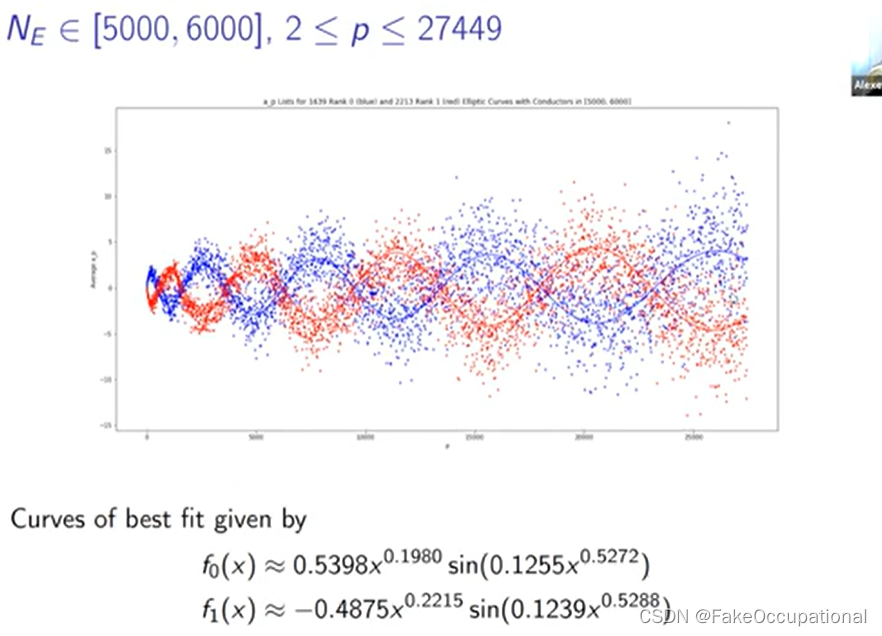
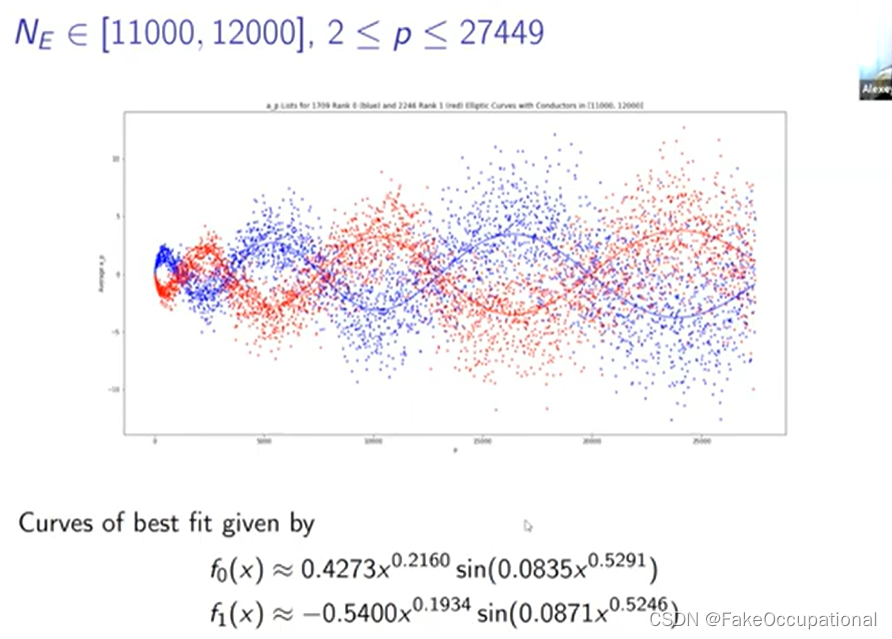
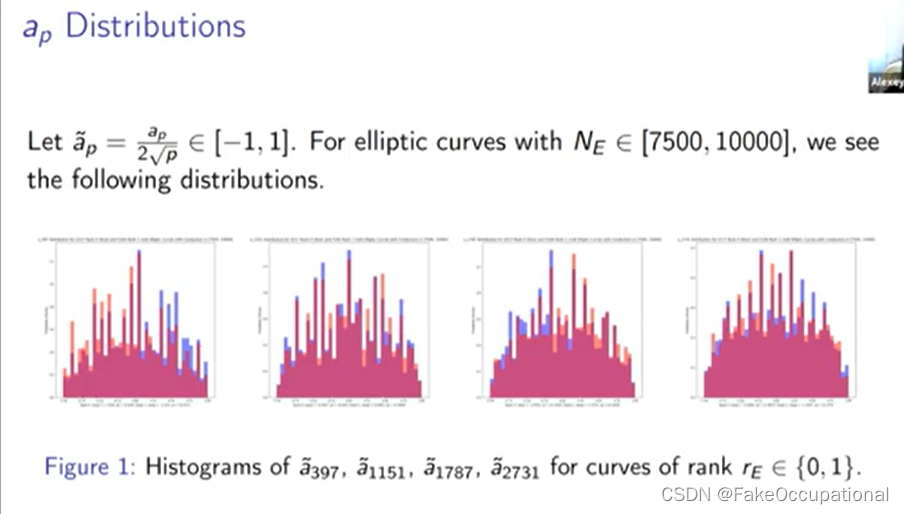
-
我们将排名零的分布绘制为蓝色,将排名一的分布绘制为红色,大多数分布是这个紫色重叠区域
-
我想简要谈谈我们一直在研究的这项工作的非常自然的延伸之一,所以嗯安德鲁·怀尔斯(andrew wiles)当他批准马的最后一个定理时,他的一个非常重要的关键步骤是他证明了某个椭圆曲线是模的,这意味着 l 函数将椭圆曲线与 a 的 l 函数关联起来或等于 a 的 l 函数某种模块化形式。从那时起, 这个结果得到了某种程度的扩展,特别是在 2001 年证明了有理数上的所有椭圆曲线都是模的,

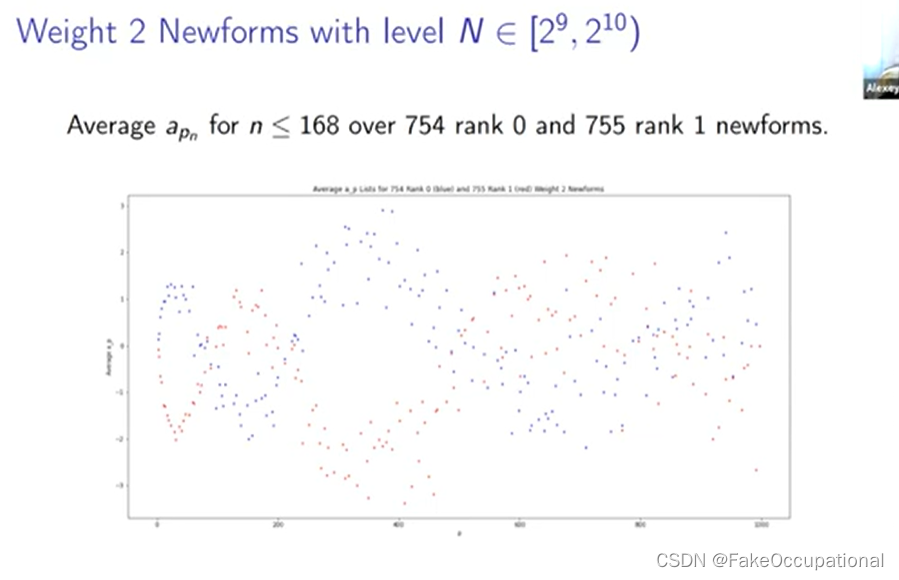
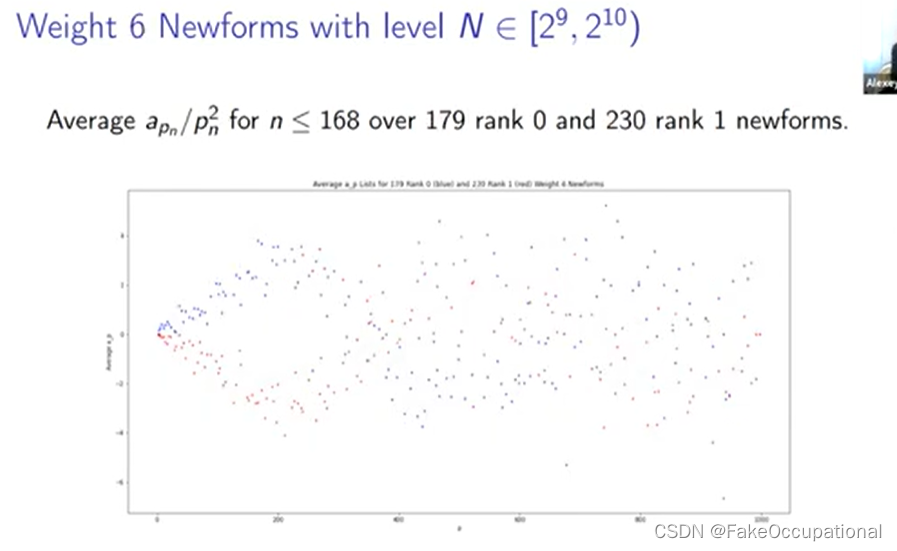
New Questions

相关文章:

bsd猜想 Murmuration of Eliptic Curves(笔记)
BSD Alexey Pozdnyakov (University of Connecticut) YUTUBE视频, B站搬运地址新生代女数学家Nina Zubrilina得到椭圆曲线椋鸟群飞模式精确公式与证明 Arithmetic Geometry算术几何 希尔伯特第十问题 希尔伯特第十问题(Hilbert’s Tenth Problem&#…...

小米汽车正式发布:开启智能电动新篇章
随着科技的不断进步,汽车产业正经历着前所未有的变革。智能电动汽车作为这一变革的重要方向,正吸引着越来越多的目光。在这个充满机遇和挑战的时代,小米汽车凭借其卓越的技术实力和深厚的市场底蕴,终于迈出了坚实的一步。今天&…...

线性代数笔记25--复数矩阵、快速傅里叶变换
1. 复数矩阵 复向量 Z [ z 1 z 2 z 3 z 4 ⋯ ] Z\begin{bmatrix} z_1\\z_2\\z_3\\z_4\\ \cdots \end{bmatrix} Z z1z2z3z4⋯ 复向量的模长 ∣ z ∣ z ‾ ⊤ z [ z ‾ 1 z ‾ 2 z ‾ 3 ] [ z 1 z 2 z 3 ] \lvert z\rvert\overline z^{\top}z \begin{bmatrix…...

洛谷 P8783 [蓝桥杯 2022 省 B] 统计子矩阵
题目描述 给定一个 NM 的矩阵 A,请你统计有多少个子矩阵 (最小 1111, 最大 NM 满足子矩阵中所有数的和不超过给定的整数 K。 输入格式 第一行包含三个整数 N,M 和 K。 之后 N 行每行包含 M 个整数, 代表矩阵 A。 输出格式 一个整数代表答案。 输入输出样例 …...

Rust 实战练习 - 8. 内存,ASM,外挂 【重磅】
目标: C写一个Demo版本的游戏由浅入深,了解外挂原理Linux/Android下实现内存读取ptrace实现内存修改(依赖第三方库) 先准备一个C写的小游戏 #include <stdio.h> #include <string.h>struct Role {float pos_x; // …...
XUbuntu22.04之Typora快捷键Ctrl+5不生效问题(二百二十六)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...

GRE_MGRE综合实验
目录 1、R5为ISP,只能进行IP地址配置,其所有地址均配为公有IP地址。 IP配置 配置公网全网通 2、(1)R1和R5间使用PPP的PAP认证,R5为主认证方。 PAP认证 (2)R2与R5之间使用ppp的CHAP认证&am…...

把组合损失中的权重设置为可学习参数
目前的需求是:有一个模型,准备使用组合损失,其中有2个或者多个损失函数。准备对其进行加权并线性叠加。但想让这些权重进行自我学习,更新迭代成最优加权组合。 目录 1、构建组合损失类 2、调用组合损失类 3、为其构建优化器 …...

用Bat启动jar程序
前情提要:在使用冰蝎、哥斯拉等一些列工具时(PS:一系列需要利用Java环境并打开的jar),我就在想能不能写一段代码点一下,就能打开程序而不用去输入命令 echo off echo 程序启动中... start javaw -noverif…...

网站维护页404源码
网站维护页404源码,布局简洁,上传即可使用。 网站维护页404源码...
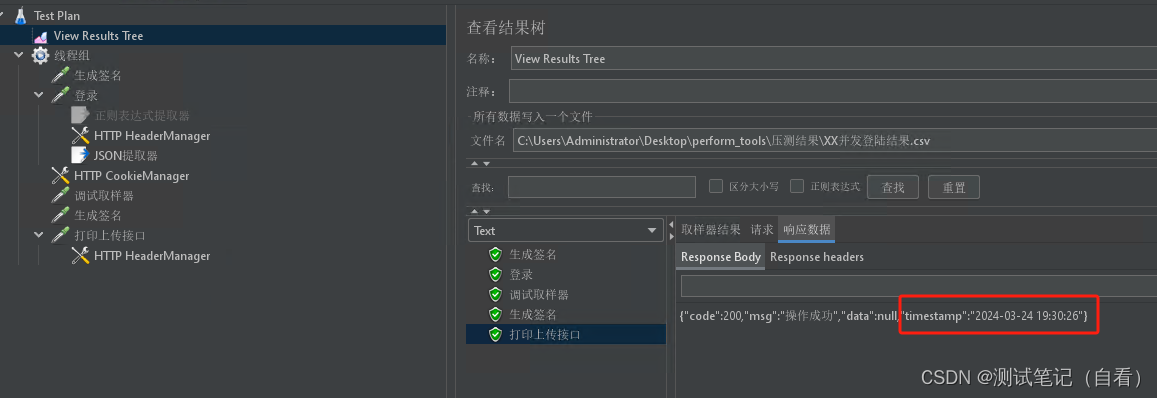
jmeter链路压测
比如登录后返回token,业务打印上传的操作需要用到token 线程组中添加登录请求,并执行 1、添加登录并执行,查看结果 2、结果树中下拉选择正则表达式,将token参数和值复制粘贴到下方,将token值改为(.*?)࿰…...
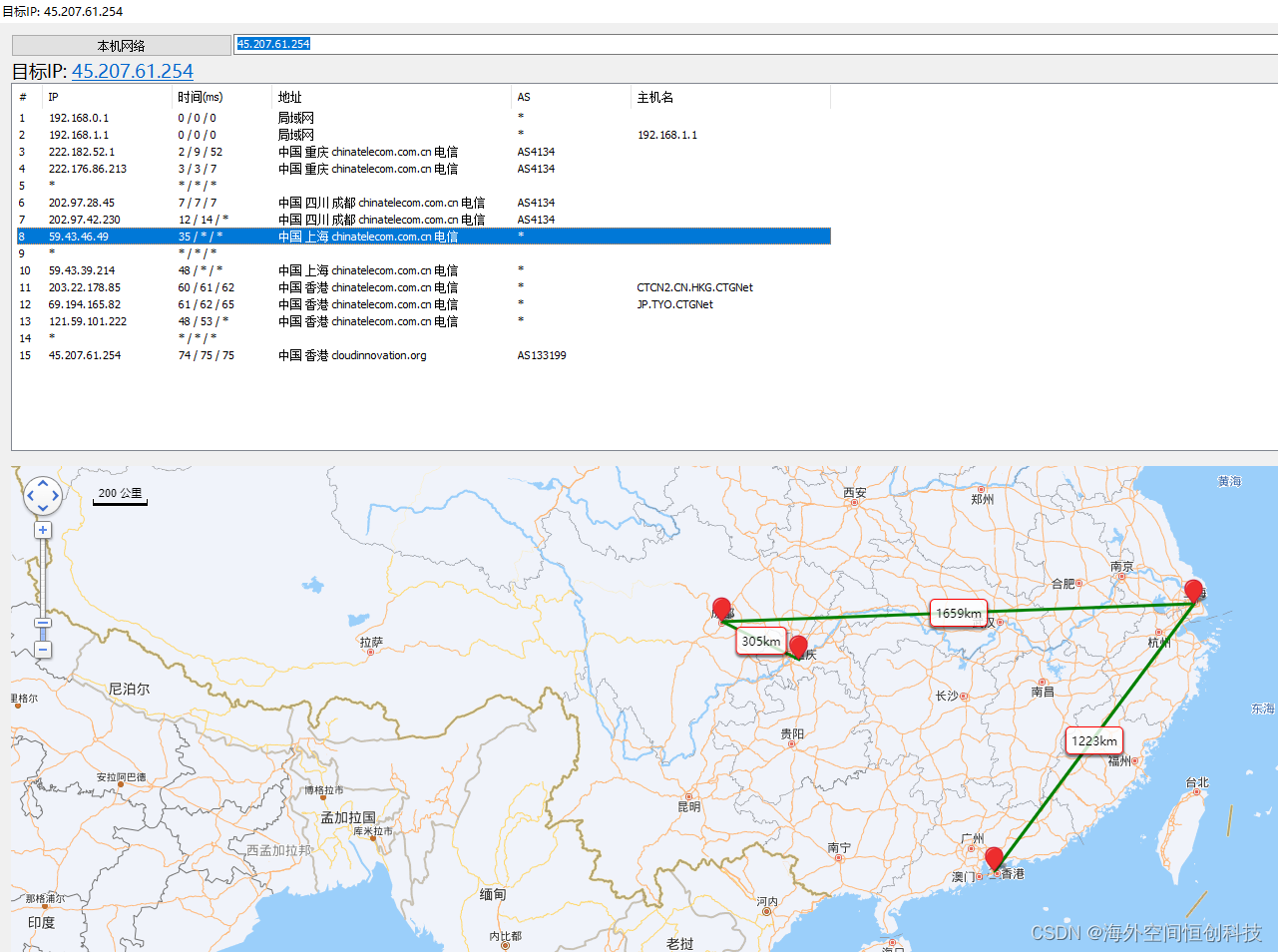
香港服务器怎么看是CN2 GT线路还是CN2 GIA线路?
不知道有没有小伙伴们注意过,很多人在租用香港服务器的时候都习惯性选择 CN2 线路?仿佛香港服务器是否采用 CN2 线路成为个人企业选择香港服务器的一个标准。其实,香港服务器有CN2、优化直连(163)、BGP多线(包含了国际和国内线路),…...

CrossOver软件2024免费 最新版本详细介绍 CrossOver软件好用吗 Mac电脑玩Windows游戏
CrossOver是一款由CodeWeavers公司开发的软件,它可以在Mac和Linux等操作系统上运行Windows软件,而无需在计算机上安装Windows操作系统。这款软件的核心技术是Wine,它是一种在Linux和macOS等操作系统上运行Windows应用程序的开源软件。 Cross…...

harbor api v2.0
harbor api v2.0 v2.0 v2.0 “harbor api v2.0”与原来区别较大,此处harbor也做了https。另外,通过接口拿到的数据也是只能默认1页10个,所以脚本根据实际情况一页页的抓取数据 脚本主要用于统计repo、image,以及所有镜像的tag数&…...

Vue 表单数据双向绑定 v-mode
每一个Vue项目,每一个系统,肯定涉及到表单的双向数据绑定问题,这一部分是 vue 的重中之重,不是因为知识点复杂,而是因为只要参与 vue 项目的开发,那么就必不可少。 单项绑定 :数据变࿰…...
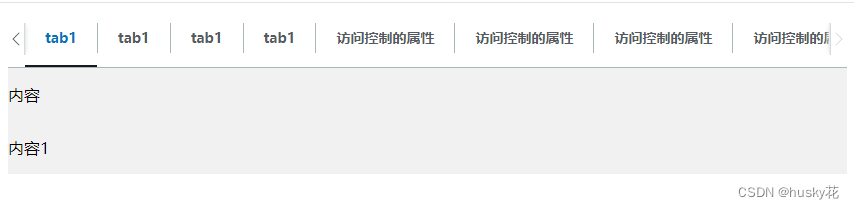
tab切换组件,可横向自适应滑动
示例图: 注:需要引入Jquery <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title><style>.tabs-box {width: 100%;height: auto;}.tab-header-box {display: flex;overflow: hidden…...

设计模式---单例模式
目录 一、五种单例模式的实现方式 1.饿汉模式 2.饿汉枚举类型 3.懒汉式 4.双检锁懒汉式 5.内部类懒汉式 二、JDK 中单例的体现 一、五种单例模式的实现方式 1.饿汉模式 public class Singleton1 implements Serializable {private Singleton1() {if (INSTANCE ! null) {thro…...

HarmonyOS 应用开发之启动/停止本地PageAbility
启动本地PageAbility PageAbility相关的能力通过featureAbility提供,启动本地Ability通过featureAbility中的startAbility接口实现。 表1 featureAbility接口说明 接口名接口描述startAbility(parameter: StartAbilityParameter)启动Ability。startAbilityForRes…...

BaseDao封装增删改查
文章目录 什么是BaseDao操作代码增删改查询单个数据查询多个数据 总结 什么是BaseDao BaseDao是: 数据库里负责增加,删除,修改,查询 具体来说是一种接口代码,公共方法的接口类。 在dao层新建basedao,其他dao层接口继承basedao 相…...

Redis入门到实战-第十三弹
Redis入门到实战 Redis中JSON数据类型常见操作官网地址Redis概述JSON常见操作更新计划 Redis中JSON数据类型常见操作 完整命令参考官网 官网地址 声明: 由于操作系统, 版本更新等原因, 文章所列内容不一定100%复现, 还要以官方信息为准 https://redis.io/Redis概述 Redis是…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...
